含可再生能源的配电网动态重构启发式方法

陈伟伟，边家瑜，常 鹏，周连凯，熊紫维，王 威

(1.国网新疆电力有限公司经济技术研究院，新疆 乌鲁木齐 830002) (2.山东科技大学智能装备学院，山东 泰安 271019)

配电网动态重构方法主要有基于时段划分动态重构、智能算法和静态重构启发式方法等。王淳等[1]采用模糊C均值聚类算法基于负荷相似性实现重构时段划分；文娟等[2]以负荷变化的数学特征为依据确定重构时段。考虑到单项指标全局代表性较弱，田昊等[3]提出以综合性能为依据进行重构时段求解；张珂等[4]提出基于隶属度函数实现重构时段划分。然而，重构时段数的确定具有一定的主观性，各时段划分方法无法确保所得重构结果全局最优。为此，智能优化算法凭借强大的随机搜索能力，理论上可以获得最优解，在配电网动态重构中得到广泛的应用研究，熊宁等[5]提出了基于开关组禁忌搜索算法的动态重构求解模型；孙惠娟等[6]提出以代数连通度快速消除无效解，在此基础上采用复合微分进化算法寻优。但是不同的配电网络在使用智能优化算法时需要不同的参数设置，缺乏通用性，且对大规模网络的计算效率低。为了提高算法的通用性和计算效率，基于静态重构的启发式方法得到了青睐，李振坤等[7]提出采用粒子群算法实现各时段静态寻优，基于多代理系统技术实现动态耦合；曹昉等[8]采用改进细菌觅食算法进行静态重构求解，对静态结果引入开关相似度进行时段合并实现动态重构；Guimares等[9]采用贪婪启发式方法静态求解，以多准则决策过程确定最终动态方案；Shariatkhah等[10]采用和声搜索算法确定各时段最优的网络拓扑，以动态规划实现各时段重构方案耦合。然而上述文献在对开关动作次数削减的处理中,没有考虑单次开关动作次数削减收益最大化，导致开关动作次数相同的情况下经济性未能达到或接近最优。

1 基于高斯混合分布的风光随机出力场景

高斯混合模型(Gauss mixed model，GMM)如图1所示，其本质上就是融合了多个单高斯模型，可以逼近任意的概率分布密度函数。有限个高斯混合模型逼近未知分布密度函数时，具有逼近精度高的优点。GMM概率密度分布函数φ(x)表示为：

(1)

(2)

mi>0

(3)

式中：x为随机变量，本文中表示风或光出力；s为高斯分量数；mi为第i个高斯分量的权重；σi为第i个高斯分量的标准差；μi为第i个高斯分量的均值。

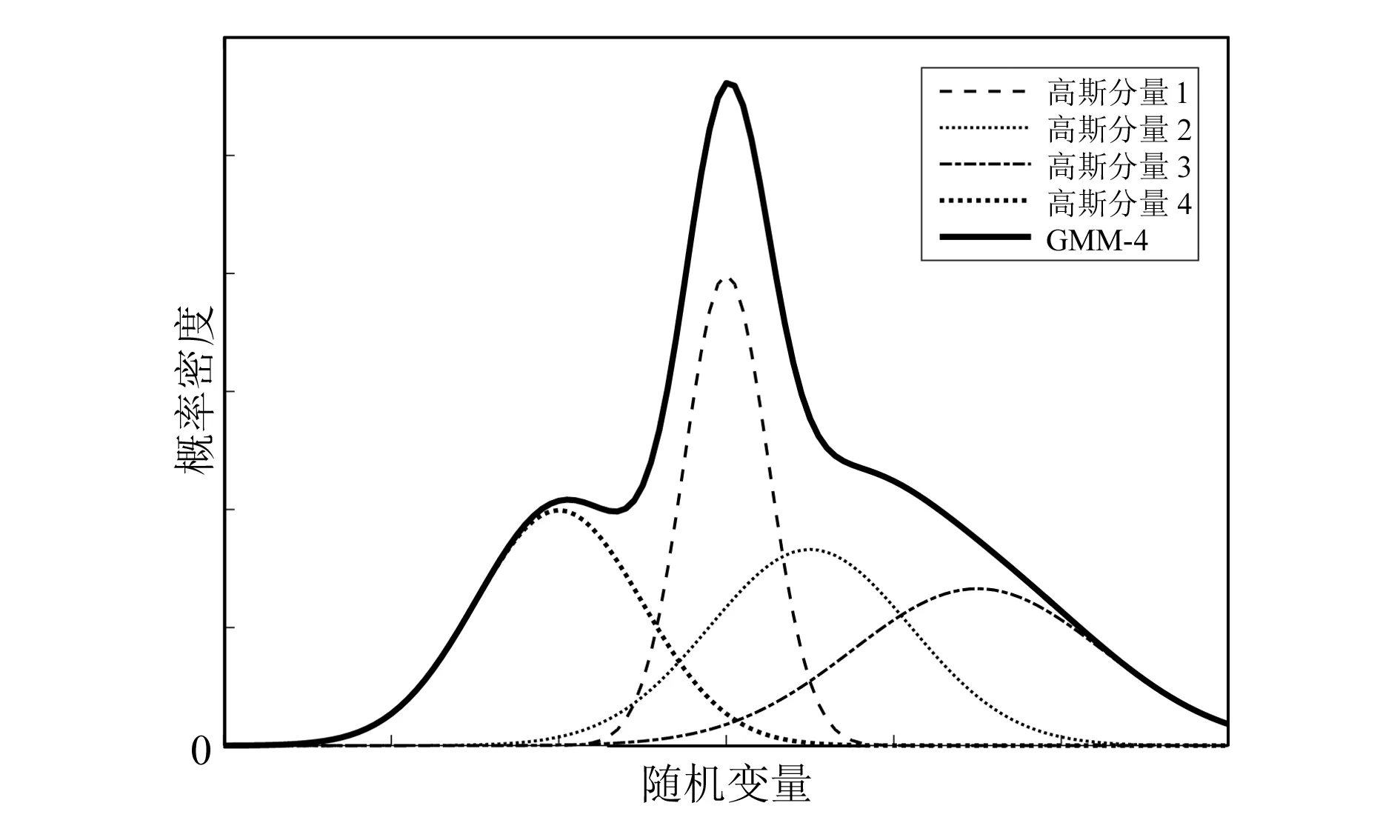
图1 高斯混合分布模型

高斯混合分布模型的难点在于求解各个参数，限于文章篇幅，各参数的求解方法本文不作详细介绍。采用参数估计理论，确定混合模型中高斯分量数s，并用对数似然函数来确定其余各高斯分量参数。基于各可再生能源出力分布模型，建立风、光出力关键场景。将各高斯分量划分为7个区间，以各区间中值xi,k代表该区间随机变量，不同高斯分量分布函数的区间划分可能存在交叉和重合现象。为简化计算，若出现交叉现象取其中概率值大的中值，对各区间进行积分得到中值xi,k对应的概率值p(xi,k)，i=1,2,…,s,k∈[1,7]。对时段t内具有相同出力值的各高斯分量的概率求和，得到当前出力值xk,t对应的概率p(xk,t)：

(4)

24小时各时段风、光随机出力组合构成不同的场景ω：

ω={xk,1,xk,2,…,xk,24}

(5)

场景ω发生的概率pω：

(6)

随着时段的增加，产生的场景数将呈指数级递增，为提高计算效率，同时考虑到其中很多场景发生的概率极低，没有必要对其进行分析，将生成的场景ω按照其发生的概率pω进行排序，选择其中概率值较大的场景进行分析，由此生成关键场景即24小时风、光出力与其对应的概率{ωn,pωn}，pωn为场景ωn发生的概率。

2 动态重构模型和求解方法

基于上述生成的场景建立配电网动态重构期望值模型，期望值是指在一些期望约束条件下，决策者希望做出的决策能够实现最大的期望回报。

2.1 数学模型

本文建立当前重构方案在各场景下以网损ploss的期望值E(ploss)最小为目标的数学模型，目标函数如下：

(7)

式中：m为场景数；PFa(ωn),loss为场景ωn在重构方案Fa下的网损。

(8)

式中：b为网络支路总数；rij为支路(i,j)的电阻，其中i,j表示支路的首末端节点；φij,t为支路(i,j)在时段t的状态，是一个二元变量，若支路(i,j)闭合φij,t为1，反之则为0；Pij,t,Qij,t分别为支路(i,j)在时段t流经的有功功率和无功功率；Ui,t为节点i在时段t的电压值。要实现上述目标还需要满足以下约束条件：

1)配电网潮流方程等式约束。

(9)

(10)

式中：Pi,t,Qi,t分别为节点i在时段t注入的有功功率和无功功率；Vi,t,Vj,t分别为节点i,j的电压值；N为节点数；Gij,Bij,θij,t分别为支路(i,j)的电导、电纳和相位角差。

2)节点电压约束。

Ui,min≤Ui≤Ui,max

(11)

式中：Ui,min,Ui,max分别为节点i的电压Ui的下界和上界。

3)支路容量传输约束。

Sij≤Sij,max

(12)

式中：Sij为支路(i,j)的传输功率；Sij,max为支路(i,j)允许传输的最大传输功率。

4)可再生能源(renewable energy source, RES)出力约束。

PRES,λ,min≤PRES,λ≤PRES,λ,max

(13)

QRES,λ,min≤QRES,λ≤QRES,λ,max

(14)

式中：PRES,λ为第λ个RES的有功出力；PRES,λ,min,PRES,λ,max分别为第λ个RES的有功输出的最小值和最大值；QRES,λ为第λ个RES的无功出力；QRES,λ,min，QRES,λ,max分别为第λ个RES的无功输出的最小值和最大值。

5)配电网辐射状运行约束。

配电网在运行的过程中需要保持辐射状，因此在重构的过程中不能出现环网和孤岛。

6)开关动作约束。

考虑到开关寿命，重构周期内各开关不允许频繁动作，需要满足以下约束条件：

Ni≤Ni,max

(15)

∑Ni≤Nmax

(16)

式中：Ni为第i个支路开关的总动作次数；Ni,max为第i个支路开关的最大允许动作次数；Nmax为所有开关允许的最大总动作次数。

2.2 求解方法

基于第1章提取的典型场景，采用改进最优流模式算法求解各时段的静态重构方案，并记录重构周期内各开关动作情况。如果上述各关键场景的静态重构方案能够满足式(15)和式(16)，那么所得各时段静态重构方案即为动态重构结果；若不满足，则需要对静态重构方案按时序进行耦合，削减开关动作次数，直至开关同时满足单个开关和总开关动作约束。考虑到开关动作约束包括单个开关和总开关动作约束，一般情况下，静态重构结果总开关动作次数较大，因此本文首先采用启发式规则快速对总开关动作次数进行削减，在总开关动作次数满足要求后，再判断各单个开关是否满足要求，若满足要求则计算结束，若不满足要求则以该开关的邻近开关替换，以网损增量最小为依据寻找最优或次优开关替换方案，直到所有开关都满足约束条件时结束。

j与(j-1)时段的网损增量与开关动作次数变化量的比值ratioj,j-1和j与(j+1)时段的网损增量与开关动作次数变化量的比值ratioj,j+1分别定义为：

(17)

(18)

式中：ΔPTj(·)和Δnj(·)分别为第j时段以相邻的不同静态重构结果作为当前时段网络拓扑结构后网损的增量以及开关动作次数的变化量，(j-1)表示第j时段的前一相邻不同结构，(j+1)表示第j时段下一相邻不同结构。由式(17)和式(18)计算各时段比值ratio，把ratio值从小到大顺序排列，将 值最小的时段网络结构更新为其对应的相邻结构，每次更新完之后计算开关动作次数，直至总开关动作次数满足约束条件为止。若此时存在单个开关动作次数越限，依次以邻近的开关替换，计算每次替换后的网损增量，最终以网损增量最小的开关进行替换。由静态重构基础实现动态耦合的启发式方法步骤如图2所示。

图2 开关动作次数削减启发式规则流程

3 算例分析

采用改进IEEE标准33节点系统，如图3所示，对本文所提方法进行仿真验证。该系统基准电压为12.66 kV,各节点负荷类型不同，分别为商业负荷、城市居民负荷和重工业负荷，图中节点2、3、4、14、18、19、20、21、22、23、29和31为商业负荷，节点5、6、9、10、11、12、13、15、16、17和33为城市居民负荷，节点7、8、24、25、26、27、28、30和32为重工业负荷，各典型负荷曲线如图4所示。分别在节点7、14接入额定功率为500 kW的光伏(photovoltaic, PV)，在节点10、33接入额定功率为400 kW的风机(wind turbine, WT)，切入风速为3 m/s，额定风速为11 m/s，切出风速为25 m/s。设定单个开关最大动作次数为3，所有开关最大总动作次数为16。

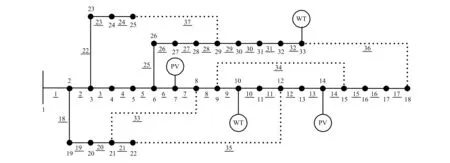
图3 改进IEEE-33节点配电网络

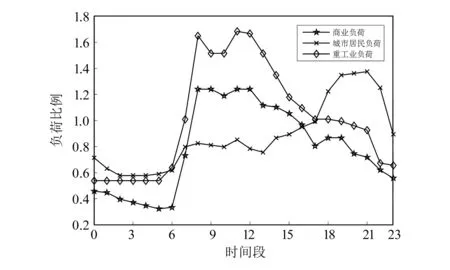
图4 典型日负荷曲线

基于GMM，分别给出某地夏季典型日风机和光伏随机出力场景及其概率，为减小计算复杂度，在保证场景具有较大代表性的前提下，保留5个关键场景进行分析计算，见表1，这5个场景共涵盖了97.52%的概率水平，具有较强的代表意义。

表2给出了上述场景的静态重构结果，可以看出静态重构方案开关动作较为频繁，总开关动作次数为60次，单个开关最大动作次数为9次，完全超出开关允许动作限制，因此有必要对开关动作进行削减。

表1 风机和光伏出力典型场景及其概率

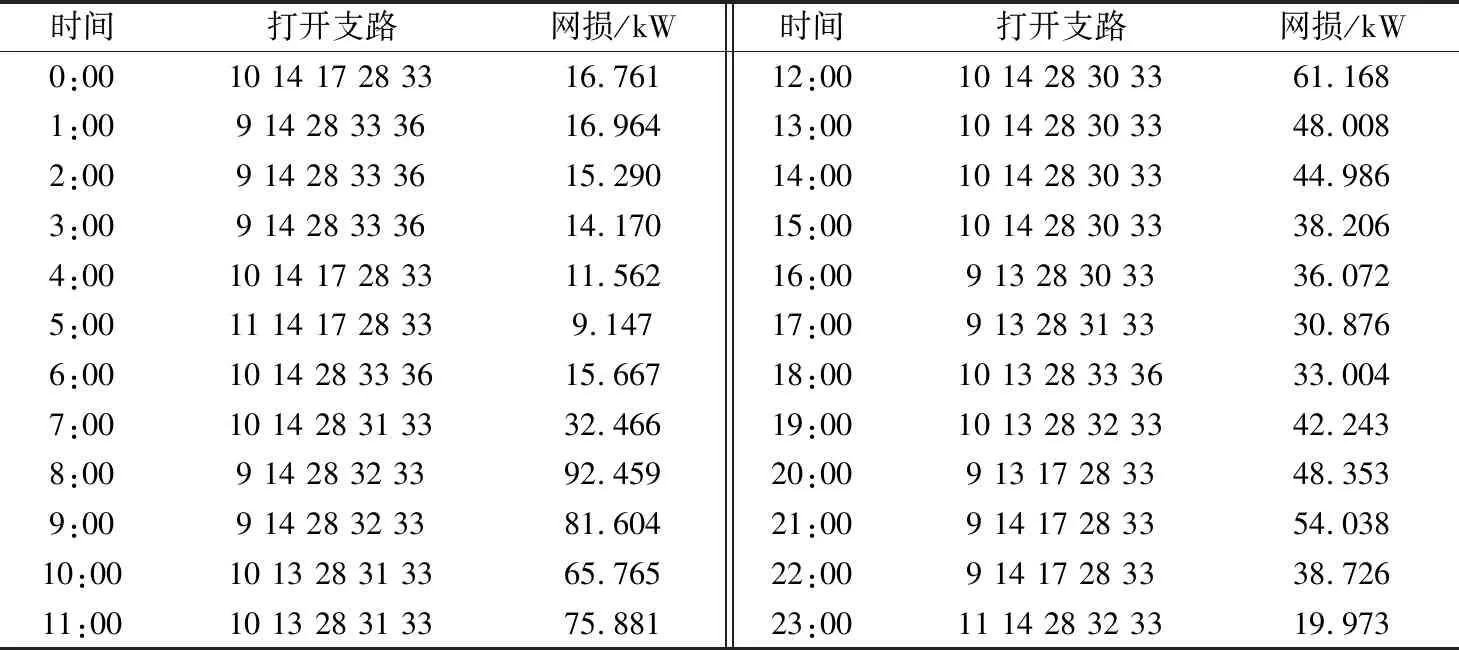
表2 静态重构方案

以协调优化方法对上述静态重构方案进行耦合。为提高开关的利用率，在开关允许的动作次数内各开关尽可能多地动作。表3～表5给出了不同方法的动态重构过程和结果对比，可以看出在开关动作次数都为16的情况下，本文所提方法期望网损最小。

表3 本文所提方法动态重构过程

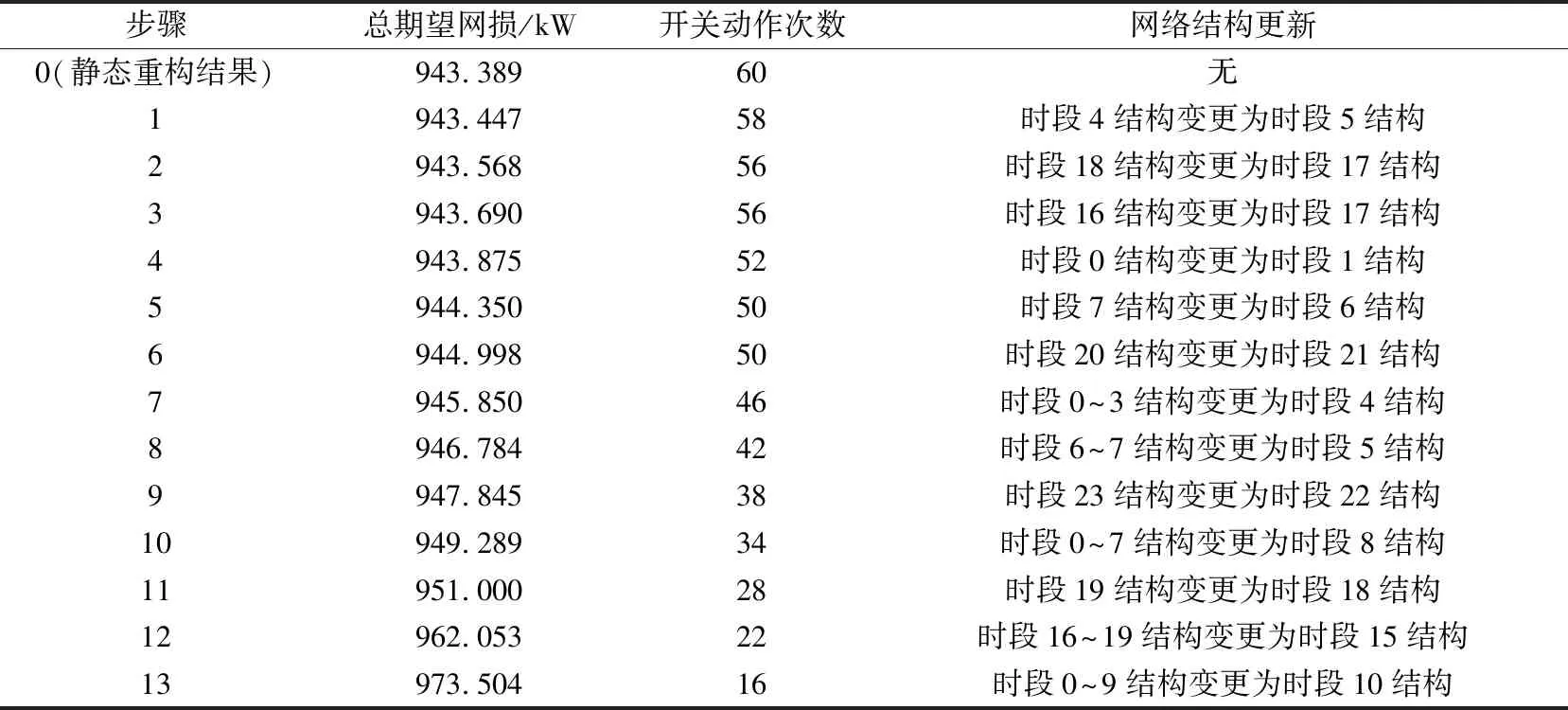
表4 文献[7]所提方法动态重构过程

由上述计算结果可知，在所有开关动作都满足约束条件的前提下，总开关动作次数取最大允许上限16，本文所提动态重构方法总期望网损为960.968 kW，比原始网络期望网损1 305.823 kW下降了26.41%，而文献[7]的期望网损相对于原始网络期望网损下降25.45%。可以看出，本文所提方法降损百分比更大，在开关动作次数相同的情况下，具有更好的寻优能力。这是因为本文所提启发式方法基于网损和开关动作次数变化量的比值进行开关动作次数削减，每次决策都是依据单次开关削减后使网损增量最小进行的。需要注意的是，在开关动作次数削减的过程中，如果仅考虑网损变化，可能会导致有限的开关动作次数分配不合理，使得最终的降损效果不理想。

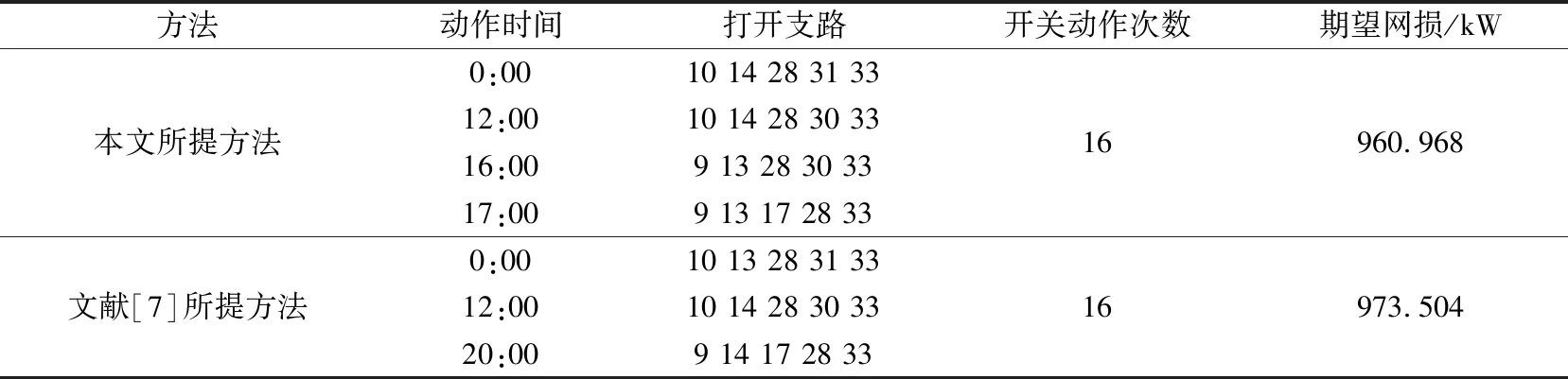
表5 两种不同方法动态重构结果对比

4 结束语

本文提出了一种基于期望值约束的动态重构方法，采用混合高斯分布模型提取典型场景，以1 h为间隔对各场景进行静态网络重构求解。基于开关动作约束，以网损增量和开关动作次数变化量的比值为启发式规则实现重构周期内总开关动作次数削减，以邻近开关替换单个动作次数越限的开关。仿真结果表明，本文所提方法在静态重构基础上具有更好的动态寻优能力，可以为配电网动态重构提供科学指导，所提期望值模型可以推广到其他不确定性问题的优化决策中。