民用飞机大变形静气动弹性载荷设计

谭林林，杜云龙

(上海飞机设计研究院，上海 201210)

随着飞行器设计技术以及复合材料技术的发展，多飞行任务以及大飞行包线成为现代大型飞机的设计需求。飞机结构柔性大[1-2]，弹性效应开始突显，传统的线性气动弹性分析手段无法满足要求，对此类大变形的柔性飞机不能进行准确的结构动力学描述和气动力建模，由此提出了大变形几何非线性[3-4]气动弹性载荷设计技术。

本文通过研究结构几何非线性效应以及曲面气动力效应[5]对静气动弹性载荷的影响，详细分析了民用飞机考虑非线性效应的弹性载荷分布特性，通过比较线性与非线性弹性载荷的差异，表明了在对大柔性飞机进行静气动弹性载荷分析时，必须同时考虑结构非线性和气动力非线性。

1 计算方法

在进行工程分析时，线性静气动弹性载荷计算中气动力建模通常采用偶极子格网法，但偶极子格网法无法跟随结构变形形成曲面，因此不再适用大变形的非线性静气动弹性载荷分析。针对大变形载荷分析时气动网格要跟随结构变形的特点，本文中的气动网格建模选取曲面涡格法来求解定常气动力。在静气弹迭代中，只有始终根据结构变形更新气动模型，才能够反映气动面如何随着结构的弯、扭变形，即曲面的跟随效应[6]。曲面气动力效应是影响配平攻角及载荷分布的重要因素，一方面，随着结构的弯曲变形，机翼的有效升力面积减小，从而需要更大的配平迎角；另一方面，机翼弹性变形造成的扭转会改变各个剖面的有效迎角，影响载荷大小和分布情况。结构几何非线性对柔性飞机的影响，主要体现在两个方面：一是结构整体刚度因不同的载荷状态而改变；二是机翼平面形状的改变影响到气动力的分布。本文基于非线性有限元理论，建立结构有限元模型，进行静气动弹性分析。

1.1 曲面涡格气动力模型

曲面涡格法能够较好地模拟大变形产生的曲面气动力效应。曲面涡格模型示意图如图1所示，将变形后的机翼中弦面划分成若干四边形网格进行气动力求解，坐标系的x轴沿来流方向，y轴水平向右，z轴通过右手定则确定。每一个网格内布置一个涡环，气动力采用曲面涡格法进行求解。涡环单元由4段等强度直线涡首尾相接而成，翼面一部分涡由后缘涡格拖出，形成尾涡，平行于来流方向，其几何关系如图2所示。选取涡格1/4弦线中点为力作用点(图中用符号“○”表示)，涡格3/4弦线中点为控制点(图中用符号“×”表示)，在控制点处满足涡格法向不可穿透的边界条件。

图1 曲面涡格法示意图

图2 涡环单元布置情况

物面上的涡格共有N个，N=NC·NS，其中NC为物面沿弦向网格数，NS为展向网格数；尾涡格共有M个，M=Nw·NS,其中Nw为尾涡沿弦向网格数，则法向洗流速度和涡强度的关系[5]如下所示：

(1)

1.2 几何非线性有限元方法

本文中结构不再采用小变形假设，而是考虑了变形对平衡的影响，即平衡条件建立在变形后的形状上，应变表达式包括位移的二次项，平衡方程和几何方程为非线性。本文在非线性有限元求解时采用增量法之更新的拉格朗日法[3](update Lagrange)，其中的静力学和运动学变量都参考每一载荷或时间步长开始时的位移。当考虑随动载荷情况，即结构载荷是系统状态的函数时，更新的拉格朗日法是较为有效的。

拉格朗日法应变与位移的非线性关系为：

(2)

式中：tεij为结构应变；tui,j为时刻t位移ui对坐标xj的偏导数。

1.3 非线性静气动弹性载荷分析方法

结合以上几何非线性有限元理论和曲面定常气动力计算方法，对具有几何非线性特点的大展弦比民用飞机结构进行几何非线性气动弹性分析，建立具有结构几何非线性的气动弹性方程。

本文主要采用曲面气动力计算与几何非线性结构有限元迭代计算的方法得到全机的非线性静气动弹性平衡状态，从而完成静气动弹性非线性结构变形分析与载荷分析。由于机翼的变形与气流的作用力有关，而气动力又与机翼在空中的形状和位置有关，因此两者是相互影响、相互制约的非线性关系。静气动弹性分析方法如图3所示。

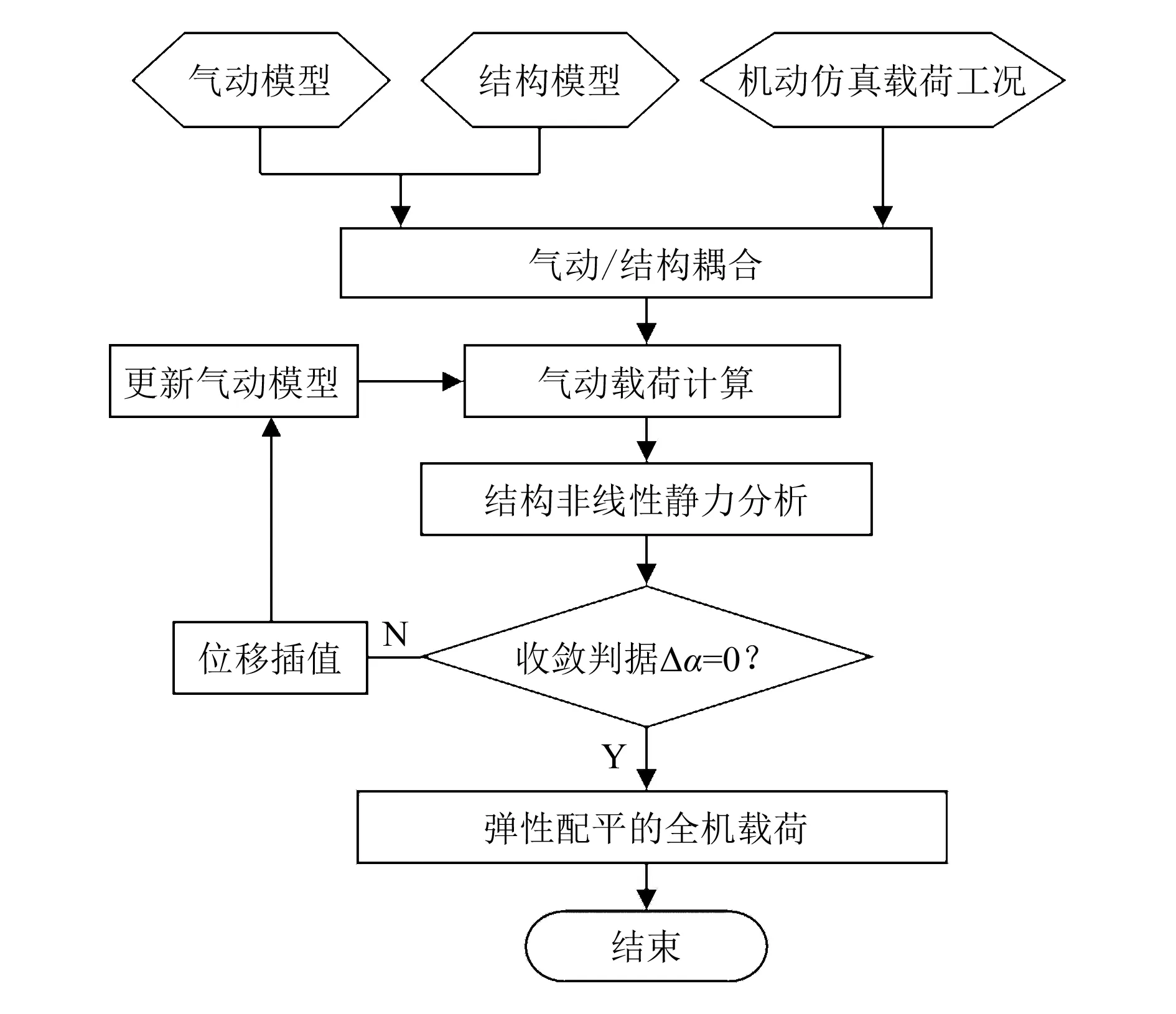
图3 静气动弹性分析

2 算例分析

本文以某大柔性民用客机为例，基于几何非线性效应的结构、气动建模方法和静气动弹性配平方法，进行全机非线性静气动弹性载荷分析，并与传统的线性气动弹性载荷分析结果进行对比分析。

2.1 结构有限元模型

该模型由机身、机翼、翼吊发动机、平尾、垂尾组成，主要承力结构均为梁单元。机身与机翼、平尾使用广义柔度阵GENEL[4]单元连接，机身上分布有集中质量单元，与机身的梁单元通过多点约束MPC(multipoint constraint)[4]连接。为适应几何非线性有限元计算及载荷的随动加载，对原始模型做了修改，将机身与机翼、尾翼的连接方式改为梁连接，如图4所示。

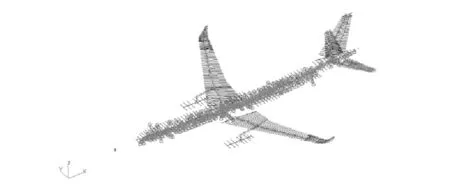
图4 结构模型

2.2 气动模型

基于曲面涡格法建立气动模型，并跟随结构变形不断修正，反映气动面随着结构变形的弯、扭变形。曲面气动力效应是影响配平攻角的重要因素，一方面，随着结构的弯曲变形，机翼的有效升力面积减小，从而需要更大的配平迎角；另一方面，机翼弹性变形造成的扭转会改变各个剖面的有效迎角，影响气动力的大小和分布情况，如图5所示。

图5 变形前后的气动面

2.3 静气动弹性分析结果

为对比说明考虑大变形几何非线性的弹性载荷影响，本文以某大柔性民机为例，选取了某载荷严重工况，分别进行非线性与线性静气动弹性载荷分析。表1给出了静气动弹性载荷配平参数，表2、表3分别给出了翼根剖面与翼梢剖面的载荷分析结果。

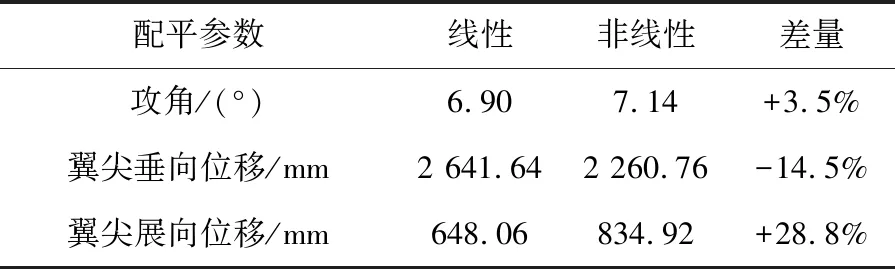
表1 静气动弹性载荷分析参数对比

由表可知，非线性静气动弹性分析得到的各剖面载荷与线性静弹性分析的结果有较大差异，非线性分析得到的剪力、弯矩、扭矩均小于线性分析结果，且在机翼不同位置处的剖面，非线性静气动弹性分析的影响效果不同，越靠近翼梢剖面，载荷减小越明显。为了研究该工况下静气动弹性载荷的具体变化情况，图6给出了线性和非线性静气动弹性分析垂向气动力沿展向的分布情况。由图可知，

图6 气动力沿机翼展向的分布情况

表2 翼根剖面载荷对比

表3 翼梢剖面载荷情况

对于该工况而言，机翼在弹性载荷作用下发生负扭转变形，而非线性法分析得到的负扭转变形量比线性分析偏小，同时可以看出，非线性静气动弹性分析得到的气动力相比线性分析向机翼根部偏移。图7和图8给出了单侧机翼主梁结点的垂向和展向位移分布情况。可以看出，对于机翼的垂向位移，非线性静气动弹性法比线性法略有减小；对于展向位移，非线性静气动弹性法比线性法大大增加，表明机翼在向上弯曲的同时，也向内侧弯曲，这样会带来显著的侧向力效应。在随动载荷的作用下，随着机翼弯曲变形的增大，侧向的位移越发显著，因此造成了展向位移上线性与非线性分析结果差异较大。

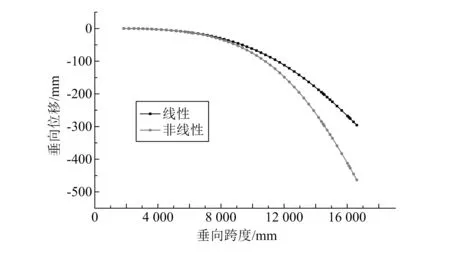
图7 机翼主梁结点展向位移情况

图8 机翼主梁结点垂向位移情况

3 结论

本文采用曲面涡格法与有限元非线性法对某大型民机进行了非线性弹性载荷的研究，并与采用小变形假设的线性静气动弹性法进行了对比分析，为后续柔性飞机的弹性载荷分析奠定了基础。主要结论如下：

1)对于大柔性飞机，考虑大变形情况，线性静气动弹性载荷分析法不再适用，本文采用曲面涡格法与非线性有限元法进行了非线性弹性载荷分析，并与线性弹性载荷分析结果进行了对比分析，证明本文所提方法可靠、合理，可用于目前大柔性飞机弹性载荷设计研制。

2)对于大柔性飞机，非线性静气动弹性载荷分析法与线性法结果存在明显差异：与线性静气动弹性载荷相比，非线性气动载荷沿展向分布更靠近翼根，即载荷内移、弯矩减小，同时非线性分析结果的负扭转小、展向位移大。