基于多分辨率梁单元模型的点阵力学性能预测

龚 赛，戴 宁，程筱胜，任利民，张伟南

(南京航空航天大学机电学院，江苏 南京 210016)

点阵结构是一种新型的轻质高强结构，由点阵单胞通过周期性阵列形成，具有超轻、高比强度、高比刚度、高能量吸收等一系列优秀的力学性能以及减振、散热、吸声等特殊性能，因此被广泛应用于汽车、船舶、航空航天等领域的轻量化需求[1-2]。由于点阵在增材制造过程中需要大量的制造成本和时间成本，因此仿真模拟的方式被广泛应用于预测点阵结构的力学性能，从而加快设计过程、节约成本。均匀化法(homogenization，HM)和有限元方法(finite element method，FEM)是模拟点阵结构力学性能的常用方法[3-4]。均匀化法涉及到代表体元法(representative volume element，RVE)的有限元分析和宏观尺度上材料属性对RVE的响应[5]。朱健峰[6]使用代表体元法研究11种点阵的等效力学性能，但是所预测的结果会因为所选取单胞个数的不同有着明显的差异。Guedes等[7]使用均匀化法对点阵的等效属性进行预测，该方法要求点阵的尺寸远小于整体结构的尺寸，在单胞数量足够多的情况下可以准确预测点阵的力学性能，但是实际工程应用中的大多数点阵都不满足这一要求。

有限元法通常通过3D实体单元精确建模或梁单元简化建模预测点阵结构的力学性能。点阵结构尺寸小、胞元数量多，如果按照3D实体单元精确建模和分析则计算量巨大，严重限制了该方法在工程中的大规模应用。采用梁单元建模分析是较为常用的点阵结构力学性能分析方法，虽然能够快速求解，大大减少计算时间，但是梁单元的使用具有一定的局限性，这种方法适用于点阵杆的直径较小、相对密度较低的情况。Ushijima等[8]采用梁单元和3D实体单元通过有限元分析研究了点阵在单向压缩载荷作用下的力学性能并和实验做了比较，指出当点阵杆径长比(d/L)小于等于0.1时梁单元和3D实体单元的有限元分析结果和实验结果一致性较好，当点阵杆径长比大于0.1时，梁单元预测的点阵结构刚度远小于实验结果，而3D实体单元所预测的结果和实验结果在大部分杆径长比范围内吻合，这表明梁单元在有限元求解中低估了点阵结构的刚度。

点阵结构杆相交区域材料的聚集将增大杆的横截面积，而梁单元为等半径模型，并没有考虑杆相交区域对点阵结构刚度的影响，因此低估了点阵结构的刚度。Luxner等[9]将梁单元节点附近所分配材料属性的杨氏模量增大1 000倍，Labeas等[10]使用梁单元在节点附近取杆长的1/10增大半径40%，以补偿对刚度的低估。Smith等[11]也采取相同的方法增加梁单元节点的刚度。

由于3D实体单元为点阵有限元求解的精确单元，能够最大程度接近实验结果，因此本文以3D实体单元模型的结果为参考，在梁单元的基础上进行修正，提出了一种多分辨率梁单元模型，以精确估计梁单元杆相交区域对点阵结构刚度的影响。

1 方法与原理

1.1 点阵结构杆相交区域对刚度的影响

如图1所示，点阵杆的相交区域对结构刚度的影响主要有两方面的原因[12]：1)在设计的CAD模型中，杆相交区域的尺寸大于杆径的尺寸；2)在增材制造点阵过程中，容易在杆相交区域发生材料聚集现象。本文只考虑设计的CAD模型引起刚度变化的影响，如图1(a)所示，在点阵结构几何建模中，需要通过布尔运算将周围杆连接，但是会导致杆相交区域的尺寸大于杆径的尺寸。在梁单元模型中，杆径是均匀的，如果用梁单元预测点阵结构的力学性能，会低估结构的刚度。

图1 体心立方点阵杆的相交区域

1.2 数学模型

为了顾及点阵杆相交区域对结构刚度的影响，本文提出一种多分辨率梁单元模型。梁单元模型是将点阵中每一根杆用长度为L、半径为R的梁参数化替代[13]，多分辨率梁单元模型是在传统梁单元模型的基础上修正为3根长度分别为L1、L2、L3，半径分别为R1、R2、R3的梁，如图2所示。

本文将传统梁单元的数学模型Bc定义为：

Bc=f(L,R)

(1)

则多分辨率数学模型Bd定义为：

(2)

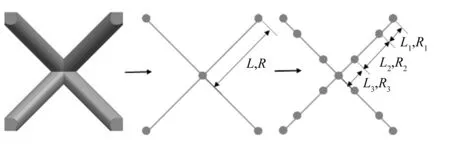
图2 多分辨率梁单元示意图

1.3 组合刚度矩阵

点阵中的杆可视为平面梁单元，节点载荷受轴向力、剪力和弯矩作用。将每根杆作为一个单元来进行有限元分析，如图3所示，每个单元有2个节点，节点1和节点2所受的轴向力分别为N1，N2，剪力分别为F1，F2，弯矩分别为M1，M2，节点位移分别为轴向位移f1，f2，横向挠度分别为Δ1，Δ2，转角分别为θ1，θ2。

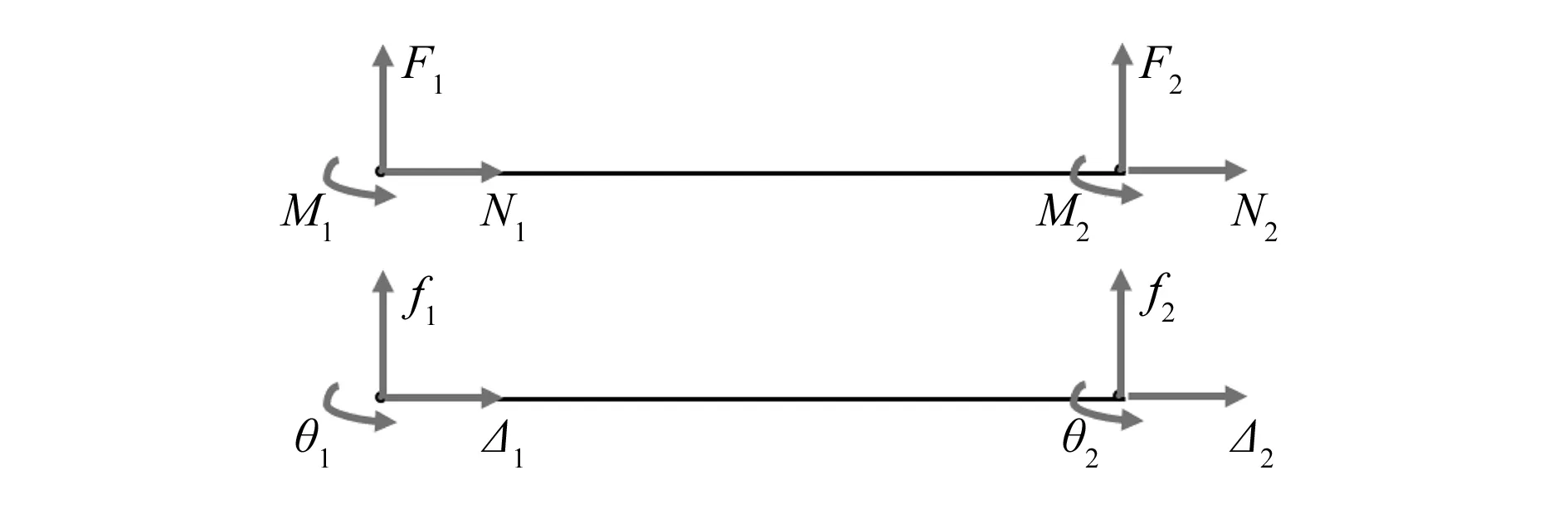
图3 受力分析示意图

由此可得单元节点的位移δ′与节点力F′为：

(3)

根据材料力学和单元刚度矩阵元素物理意义的梁单元特性，在弹性、小变形前提下，单元保持平衡时节点力和节点位移为线性关系：

F′=kδ′

(4)

式中：k为梁单元的刚度矩阵。

每次令节点位移向量的一个不同分量被单位值扰动，其他分量为0保持不变，可以求出刚度矩阵k的第一列，经过6次求解就可求出刚度矩阵的全部元素。梁单元的刚度矩阵k如式(5)所示，影响点阵中杆刚度的参数有梁单元的长度L和直径D。

(5)

式中：E为点阵结构材料的杨氏模量。

多分辨率梁单元模型如图4所示，首尾两段表示点阵结构杆与杆的相交部分，中间段表示点阵结构中杆的非相交部分，Li和Lj分别为相交部分和非相交部分的长度，Di和Dj分别为相交部分的尺寸和杆的实际尺寸。

则相交部分梁单元的刚度矩阵ki为：

ki=Cik

(6)

式中：Ci为相交部分刚度系数。此时L=Li，D=Di。

非相交部分梁单元的刚度矩阵kj为：

kj=Cjk

(7)

式中：Cj为非相交部分刚度系数。此时L=Lj，D=Dj。

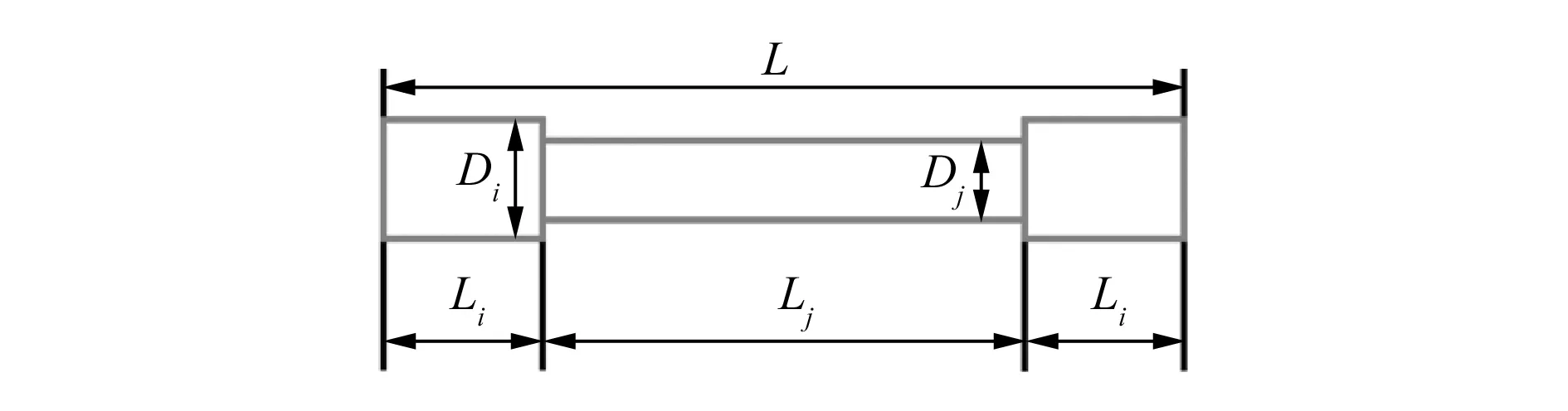
图4 多分辨率梁单元示意图

令梁单元的刚度矩阵k为：

(8)

则多分辨率梁单元组合刚度矩阵K为：

(9)

此时k1(i)～k4(i)分别为式(8)中当L=Li、D=Di时k1～k4的值；k1(j)～k4(j)分别为式(8)中当L=Lj、D=Dj时k1～k4的值。

1.4 多分辨率梁单元刚度影响系数计算方法

1.3节求出了多分辨率梁单元的刚度矩阵，通过刚度矩阵可以看出影响点阵结构刚度的是点阵结构的材料参数：杨氏模量、杆长、杆径。令CL=Li/L，CD=Di/Dj，其中CL为杆长影响系数，CD为杆径影响系数。因为在3D实体单元和梁单元中定义的材料属性相同，所以通过优化CL和CD就可以使多分辨率梁单元的仿真结果和3D实体单元的仿真结果相吻合。

为求出多分辨率梁单元的CL和CD，对3D实体单元模型和多分辨率梁单元模型施加相同的载荷和边界条件，以模拟点阵的轴向压缩行为，如图5所示。首先选择一系列不同的CL和CD以生成多分辨率梁单元模型，然后从多分辨率梁单元模型和3D实体单元模型可以分别获得一组结果。为了评估所选系数的准确性，选取3种不同杆径的体心立方(body center cubic, BCC)点阵，比较多分辨率梁单元的仿真结果和3D实体单元的仿真结果，结果吻合的系数为所选的最优杆长影响系数和杆径影响系数。所选取的点阵几何参数见表1，材料为Ti6AlV4，杨氏模量为110 GPa，泊松比为0.34。

表1 点阵几何参数

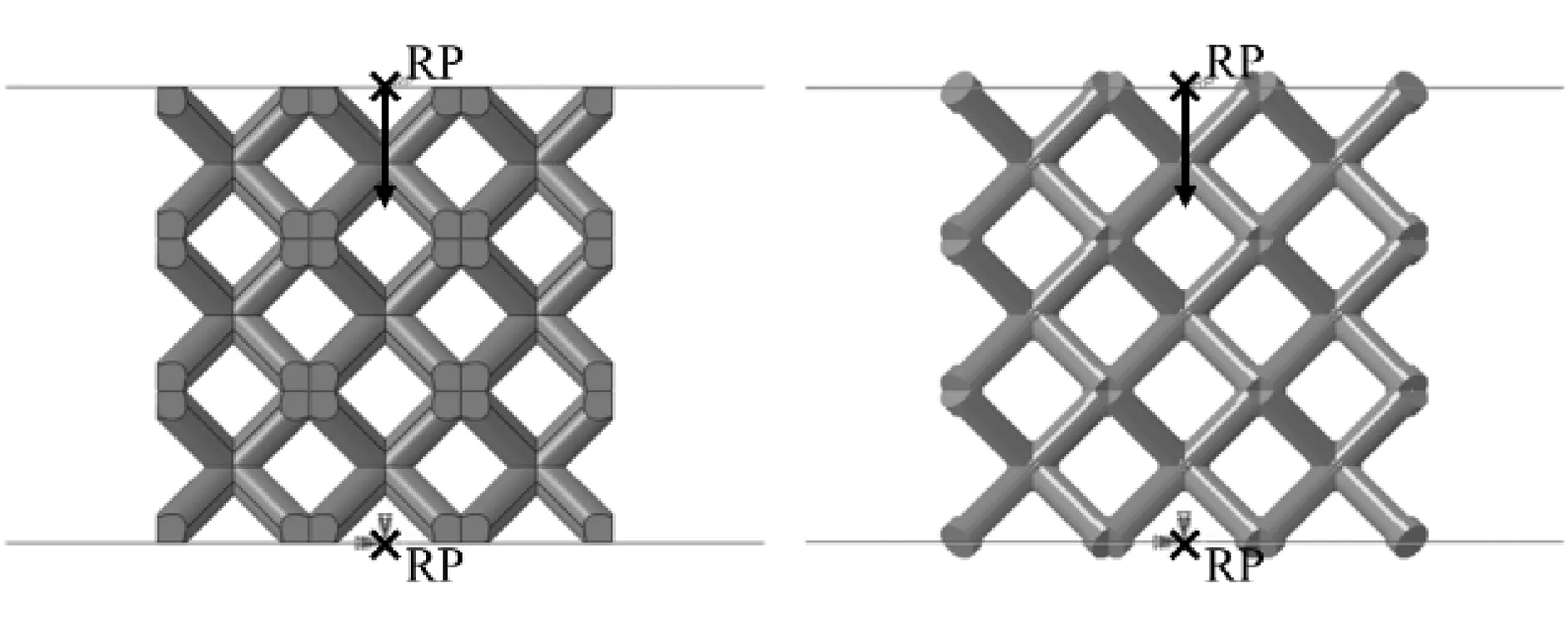
图5 点阵载荷和边界条件示意图

给予多分辨率梁单元模型的CL和CD一定的取值范围，其中CL的取值范围为1/10～1/5,CD的取值范围为1.1～2.0。将多分辨率梁单元模型得到的多个结果进行拟合，如图6所示，曲面为多分辨率梁单元模型的拟合结果，平面为3D实体单元的拟合结果，其相交曲线对应的CL和CD为多分辨率梁单元模型所取的最佳系数。此外，从图6可以看出，对于不同杆径的点阵，多分辨率梁单元模型可取的CL和CD有多个。本文进一步提出基于几何方法确定多分辨率梁单元的CL。如图7所示，首先将点阵单元用一个平面在杆的相交处剖开，得到一个不规则形状截面；将杆的相交区域近似看成一个球体，取不规则截面的最大长度的一半作为球体的半径；此半径作为多分辨率梁单元模型的CL，则CD也随之确定。

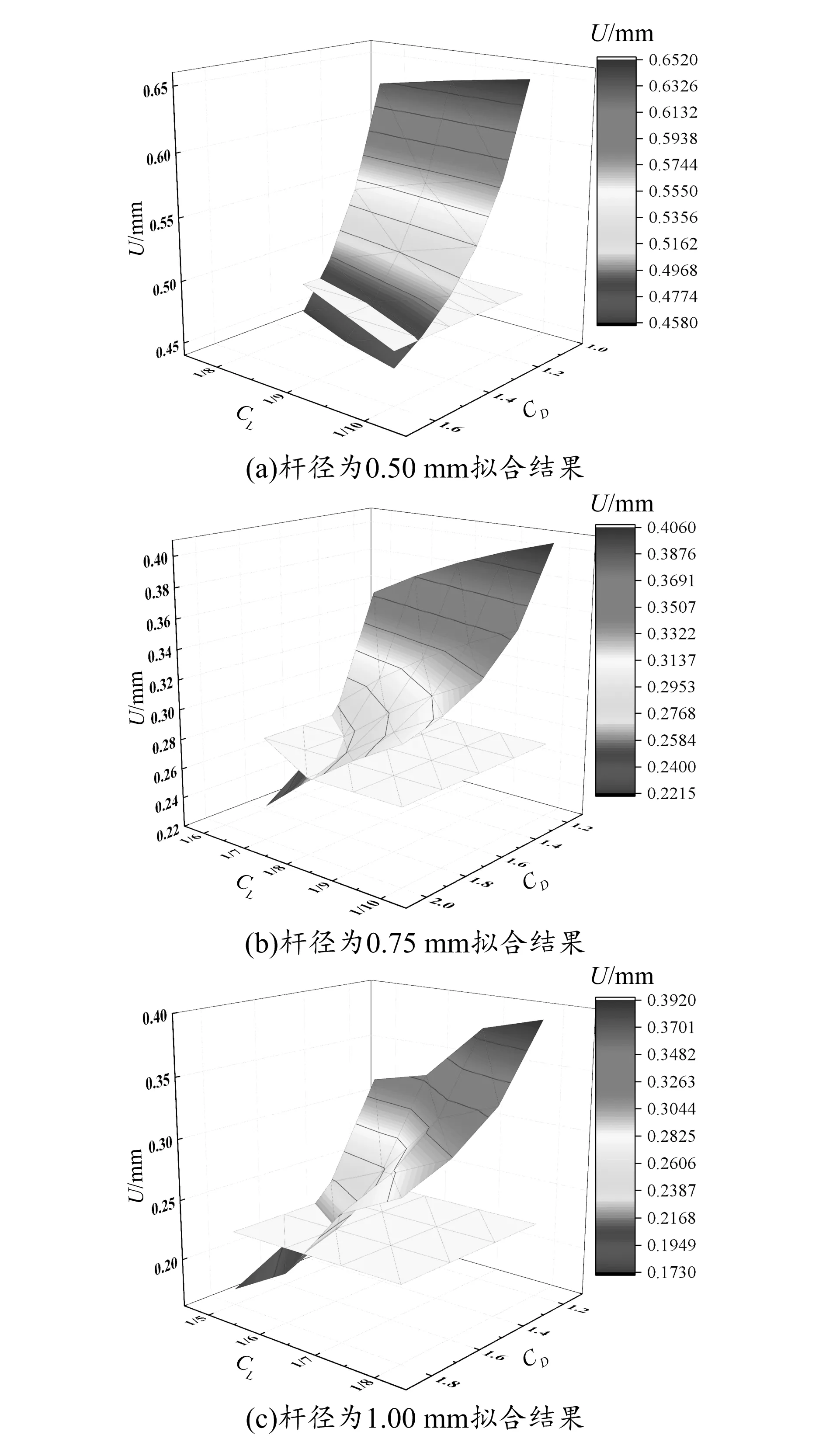
图6 不同杆径的3D实体单元和多分辨率梁单元的拟合结果

2 多分辨率梁单元模型的有效性

2.1 不同杆径点阵刚度影响系数计算

根据1.4节提出的CL和CD的计算方法，计算3种不同杆径点阵多分辨率梁单元模型的最优参数。首先按照图7所示杆长影响系数的计算方法，得出对于杆径分别为0.50 mm、0.75 mm、1.00 mm，单胞尺寸为5 mm的BCC点阵，其相交区域球体的半径分别为0.433 mm、0.645 mm、0.864 mm，然后根据相交区域球体的半径除以杆长计算出CL；最后根据图6查询、计算CD，3种杆径点阵的CL和CD最终取值见表2。

图7 杆长影响系数的确定方法

表2 多分辨率梁单元模型的最优参数

2.2 验证多分辨率梁单元有效性

为验证多分辨率梁单元模型的有效性，以3D实体单元的有限元分析结果作为参考结果验证多分辨率梁单元的预测精度。梁单元模型、多分辨率梁单元模型和3D实体单元模型采用ABAQUS/Explicit进行有限元分析[14]，如图8所示，上下两个刚体分别代表压板和基面，下端参考点固定，上端参考点施加位移载荷，参考点被用来记录点阵的反作用力和变形，通过点阵的尺寸可以转换成点阵的应力-应变数据，如图9所示。

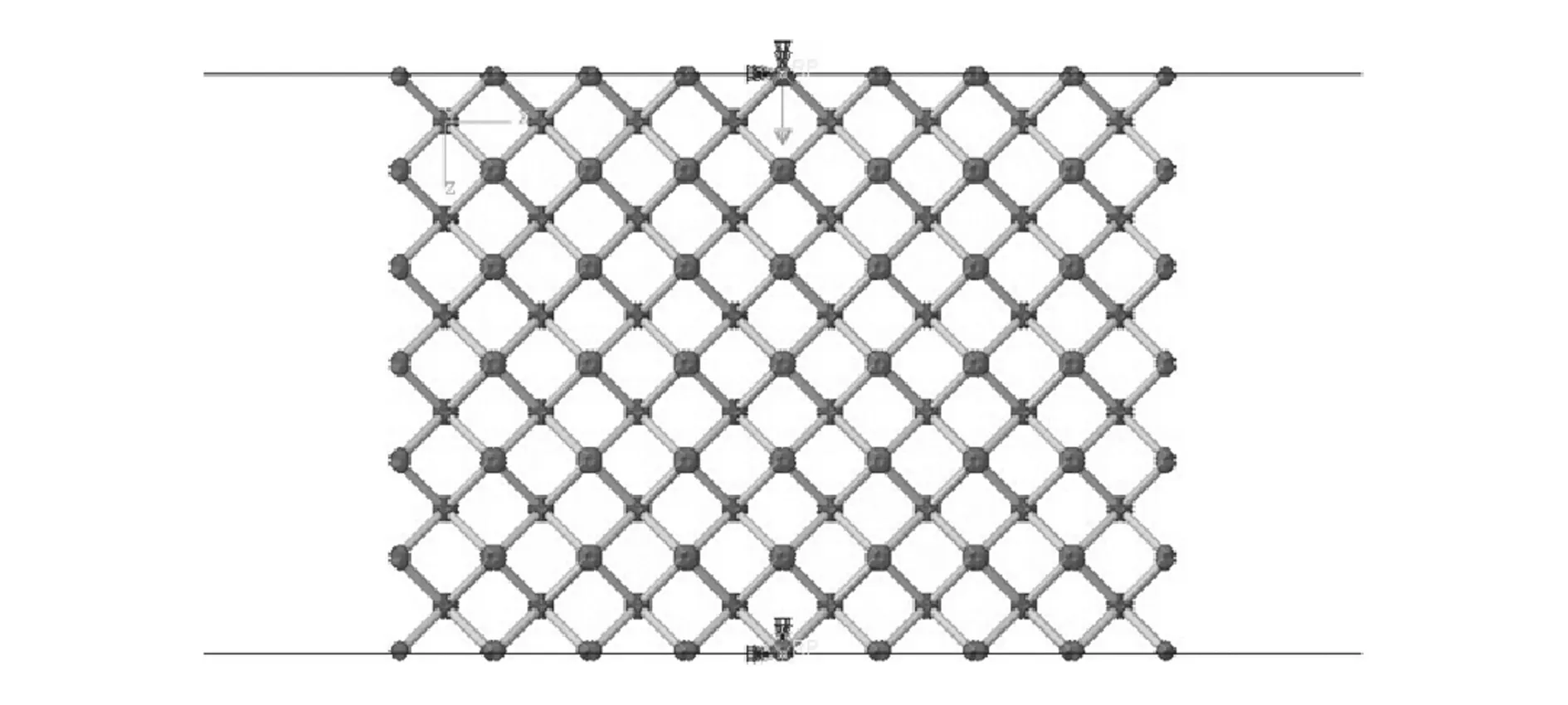
图8 多分辨率梁单元有限元模型

图9 梁单元、多分辨率梁单元和3D实体单元的应力-应变图

2.3 结果与讨论

对于3种杆径的点阵，梁单元的应力-应变曲线相比3D实体单元的应力-应变曲线相差很大，无论刚度还是抗压强度都存在很大误差；而在梁单元的基础上进行修正过的多分辨率梁单元在杆径为0.50 mm和0.75 mm时，其应力-应变曲线和3D实体单元的应力-应变曲线比较吻合；在杆径为1.00 mm时，应力-应变曲线在线弹性阶段一致性较好，而在强化阶段多分辨率梁单元相比3D实体单元有着更大的抗压强度。

3种杆径的BCC点阵等效弹性模量见表3，在杆径为0.50 mm、0.75 mm、1.00 mm时，多分辨率梁单元相比3D实体单元的误差分别为3.06%、4.86%、8.77%，随着杆径的增大，误差逐渐增大，但因点阵在实际工程应用中的杆径通常在0.50 mm和1.00 mm之间，因此本文所提出的多分辨率梁单元可以代替3D实体单元较准确地预测点阵的力学性能。

此外，本文选取的BCC点阵在X，Y，Z3个方向的数量分别为8，8，6，共有384个单胞。以杆径为0.75 mm的BCC点阵为例，3D实体单元划分网格数量为2 243 473个，求解时间为16.5 h；而多分辨率梁单元网格数量为9 216个，求解时间为3 min22 s，求解速度提高约280倍。

这表明相比于3D实体单元，经过修正的多分辨率梁单元在进行有限元分析时不仅能够节省大量的计算时间，而且能够在较大的杆径范围内保证点阵力学性能的预测精度，验证了多分辨率梁单元模型的有效性。

2.4 实验

点阵通过Renishaw AM 250选择性激光熔融技术(selective laser melting, SLM)制造，如图10所示。本文参考ASTM E9-2009(2018)室温下金属材料压缩试验的标准试验方法，采用万能试验机对点阵进行准静态压缩实验，通过压头传感器测量施加在点阵上的力，使用引伸计测量点阵的变形，压头的速度设置为1 mm/min，当观察到压力传感器上的力在很短时间内迅速下降到接近0时，实验结束。

表3 3种杆径的点阵等效弹性模量

以杆径为0.75 mm的BCC点阵为例，对在准静态压缩试验下获得的等效弹性模量与3D实体单元、梁单元以及多分辨率梁单元在准静态压缩仿真中获得的等效弹性模量进行比较，见表4。

Bai[15]在单胞尺寸为4 mm、杆径为0.8 mm时计算得到BCC点阵3D实体单元等效弹性模量约为500 MPa，而实验模量约为1 600 MPa，误差为68.75%。他将3D实体单元仿真结果和实验结果之间的偏差归因于在SLM工艺中，部分熔化的粉末黏附在点阵表面，使得制造的点阵杆径与设计杆径有差异，以及粉末的快速熔化和冷却会在结构中造成残余应力。由于加工技术的影响，制造出来的点阵杆径和设计杆径之间存在差异，这导致已加工样品的孔径、杆径和孔隙率与3D模型出现偏差，严重影响3D实体单元的预测精度。

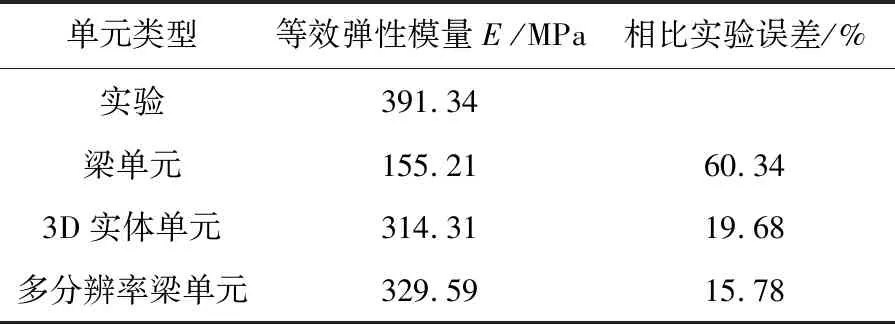
表4 不同单元等效弹性模量

图10 SLM制造的点阵

点阵在金属SLM制造中受金属粉末质量、打印参数、打印角度等多种因素耦合作用，打印出来的点阵表面粗糙度不均，导致3D实体单元的预测结果和实验结果存在一定偏差，而本文以3D实体单元的预测结果为参考，这也导致了多分辨梁单元模型的预测结果和实验结果必然存在一定偏差。

3 结论

本文考虑了点阵中杆的相交区域对结构刚度的影响，以3D实体单元的预测结果为参考，在梁单元的基础上进行修正，提出了一种多分辨率梁单元模型以补偿低估的刚度，并给出了CL和CD的确定方法。通过准静态压缩有限元仿真分析，以3D实体单元模型的结果作为参考，验证了多分辨率梁单元模型的有效性。设计并制造了3种不同杆径的BCC点阵，研究其准静态压缩特性，结论如下：

1)影响梁单元刚度的参数有杆长L、杆径D以及材料的杨氏模量；

2) 所提出的多分辨率梁单元模型解决了3D实体单元计算成本高、梁单元计算精度低的问题，在保证计算精度的同时大大降低了计算成本，因此可以用于大规模点阵结构的力学性能分析；

3) 由于金属SLM工艺因素的影响，设计的点阵杆径和制造的点阵杆径之间存在差异，这导致3D实体单元的仿真结果和实验结果存在一定差异。