基于GRA-NARX神经网络的泵站站前水位预测模型

刘晓伟，哈明虎，雷晓辉，，张召

（1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北省智慧水利重点实验室，河北 邯郸 056038；3.中国水利水电科学研究院，北京 100038）

进行长距离输水调度时，常在渠道中设置泵站等水工建筑物，以解除地形条件对输水限制的影响。泵站在运行过程中需保持水位平衡，避免出现水位大幅上升或下降等问题。若水位随时间发生较为急剧的变化，不仅可能造成泵站间弃水，甚至可能导致供水破坏或者引起整个系统的水力振荡［1］。因此，对水位信息进行处理，建立合适的泵站水位预测模型，尤其是泵站站前水位预测模型，对泵站调控、水量调度、建筑物安全等都具有重要意义。

泵站站前水位预测的方法有很多种，包括基于物理机理的水位模拟和基于机器学习的水位预测等。基于物理机理的水位模拟［2-3］，主要以圣维南方程为控制方程的水动力模型模拟一维渠道水流为主，需要研究区较为完整的资料，因此这种方法的使用存在一定局限性。机器学习方法包括向量机RVM（relevance vector machine）模型［4］、灰色系统GM（1，1）（grey model）模型［5］、多元线性回归模型［6］、神经网络模型［7-20］等，其中向量机RVM模型、灰色系统GM（1，1）模型、多元线性回归模型等的优点是适用复杂的预测任务，缺点是这些方法的预测精度有待提高。近年来，随着人工智能技术的发展，神经网络在泵站水位预测中取得了较好的效果，其中应用较为广泛的是BP神经网络。不过，BP神经网络虽然能够进行非线性拟合，但不具备反馈记忆功能。NARX（nonlinear auto-regressive model with exogenous inputs）神经网络是CHEN等［21］基于线性回归模型提出的一种非线性有源网络结构，拥有输入延迟和反馈记忆功能，能够更好地对复杂的多输入、多输出系统进行逼近模拟。目前NARX神经网络主要用于渠道流量预测、地下水位预测、旱涝预测等，如：EZZELDIN等［22］利用NARX神经网络对灌溉渠道的分水流量进行了预测，预测结果优于RBF、CFD、FFBP模型；WUNSCH等［23］利用NARX神经网络对德国西南部6眼观测井的地下水位进行预测，预测结果好；WANG等［24］利用NARX神经网络对长江流域旱涝进行预测，最后成功预测数据缺口期间的洪水事件；范哲南等［25］针对大坝变形时间序列的非线性及形变值累计特性，引入NARX神经网络进行分析并实现变形预测，且预测结果比BP神经网络好。然而，基于NARX神经网络的泵站站前水位预测模型相对较少。同时，应用NARX神经网络对时间序列预测时，使用的训练算法大多为Levenberg-Marquardt（LM），而很少对其他算法进行分析，也很少有NARX模型在时间延迟方面的探索。此外，不管采用何种预测模型，第一步可考虑筛选影响因子，这样可降低预测的复杂度并保证预测的精度。本文利用灰色关联分析（GRA）和NARX神经网络的各自优势，构建一种新的基于GRA-NARX神经网络的泵站站前水位预测模型，利用BR、LM、SCG等3种训练算法及不同时间延迟分别给出密云水库调蓄工程屯佃泵站站前水位的2 h预测结果，将模型预测结果与NARX模型和GRA-BP模型进行比较分析，并评估3种训练算法及不同时间延迟对预测精度的影响。

1 基于NARX神经网络的泵站站前水位预测模型

NARX神经网络的全称是带有外部输入的非线性自回归神经网络。它是一种有效的时间序列预测技术，是动态神经网络中的一类。泵站站前水位预测的NARX神经网络拓扑结构见图1，包括输入层、隐含层、输出层等。输入层向量为泵站当前时刻站前水位信息的影响因子，具体影响因子需经筛选后获得，输出层向量为泵站当前时刻站前水位信息。

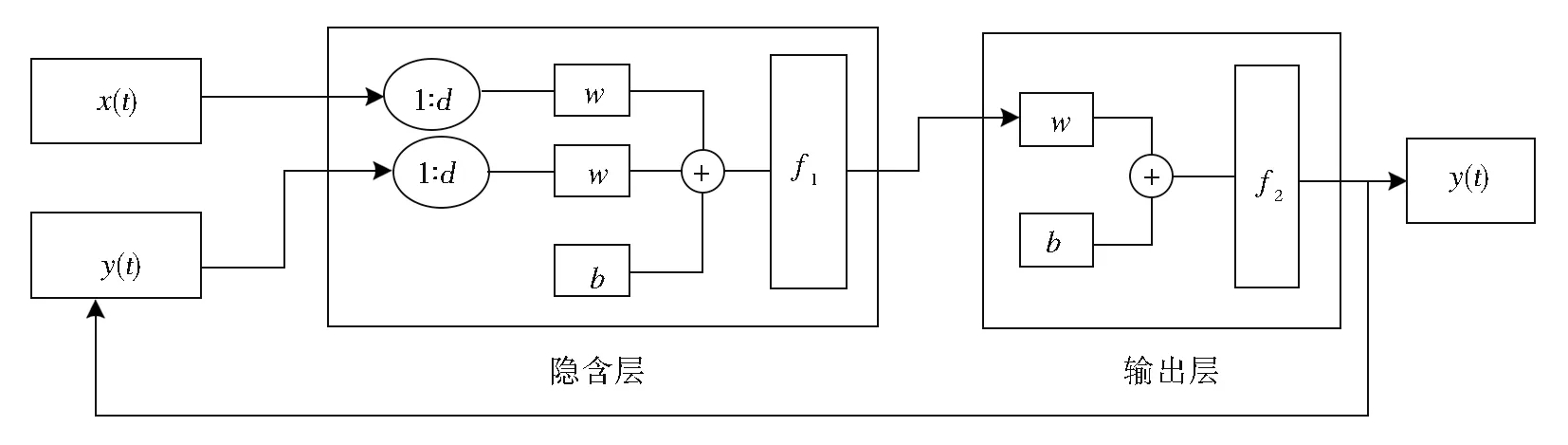
图1 NARX神经网络结构Fig.1 Structure of NARX neural network

基于NARX神经网络的泵站站前水位预测模型可表示为

式中：f为非线性函数；x（t）表示泵站当前时刻站前水位信息的影响因子，为输入变量；y（t）表示泵站当前时刻站前水位信息，为输出变量；d表示时间延迟。y（t）可由x（t）的前d个值和y（t）的前d个值，通过非线性映射得到。输入层有n个神经元，网络输入为x1，x2，…，x n，各层输出的计算公式为

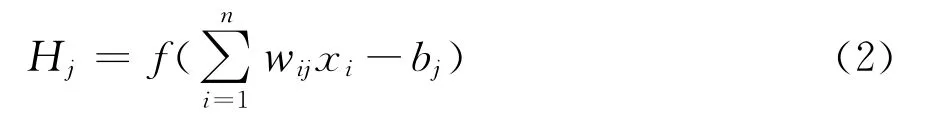
式中：x i表示神经元的输入；w ij表示层与层之间的权重；bj表示该层的阈值；f（f为f1，f2）表示激活函数。

2 基于GRA-NARX神经网络的泵站站前水位预测模型

2.1 水位监测数据清洗与插补

受设备故障、天气变化、人为干预等多种因素的影响，水情信息在采集过程中不可避免地会出现异常值。为保证预测的精度，首先需要对水情信息进行清洗。箱形图法作为一种检验样本中异常值的常用方法，与正态分布的拉依达准则、Z分数法、格拉布斯法等不同，它适用范围广，可以应用到不服从正态分布的样本数据中［26］。

箱形图中包含5个重要数据统计点，分别是被分析数据集的下四分位数S1、中位数S2、上四分位数S3、下限值、上限值。上、下四分位数之间的距离被称为四分位距RIQ，上、下限值可分别用S3＋1.5RIQ和S1－1.5RIQ表示，见图2。在图2中，分布在上、下限值以外的点即为箱形图识别出的异常值。检测出异常值后将其剔除，并对其和原有空值进行插补。

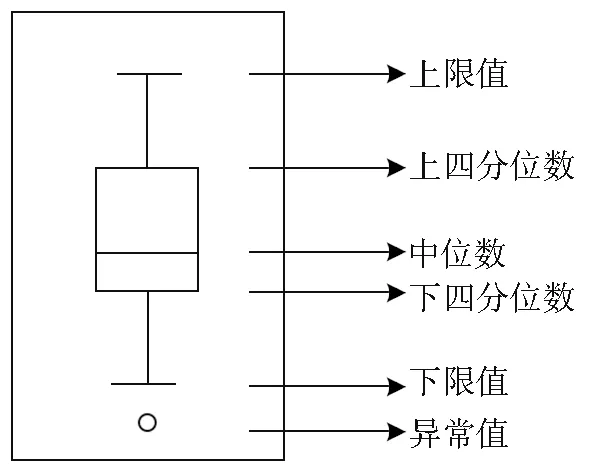
图2 箱形图Fig.2 Boxplot

2.2 水位信息的主要影响因子筛选

泵站当前时刻的站前水位信息往往受上、下游一定区域内前一个或多个时刻的断面水位、泵站流量、泵站间流量差等多种因素的影响。这些因素对水位信息的影响程度不同，存在主次影响因子。为降低预测的复杂度并保证预测的精度，只考虑主要影响因子。GRA是一种分析系统中各因素关联程度的量化方法，对样本数量多少无严格要求，数据也无须有典型的分布规律，具有广泛的适用性。具体步骤：

第一步 确定比较数列和参考数列。以被预测泵站当前时刻站前水位信息作为参考数列，泵站当前时刻站前水位信息的影响因子作为比较数列，比较数列有m个，评价指标有n个，参考数列为x0＝｛x0（k）｜k＝1，2，3，…，n｝，比较数列为x i＝｛xi（k）｜k＝1，2，3，…，n｝，i＝1，2，3，…，m

第二步 对参考数列和比较数列数据进行无量纲化处理。

第三步 计算参考数列与比较数列的灰色关联系数。灰色关联系数计算公式为

式中：ρ为分辨系数，取值区间为（0，1）。一般情况下，分辨系数ρ越大，分辨率越大；分辨系数ρ越小，分辨率越小。当ρ＝0.546 3时，分辨率最好，通常取ρ＝0.5。

第四步 计算参考数列与比较数列的灰色关联度。

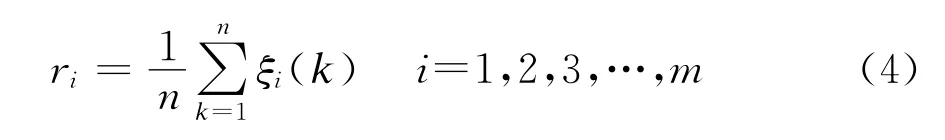
第五步 将灰色关联度按照大小进行排序，ri越接近1说明比较数列对参考数列的影响程度越高：当灰色关联度小于0.6时，认为两个数列无关；若灰色关联度大于0.8时，则认为两个数列的相关性很好。

2.3 GRA-NARX神经网络预测模型确立

GRA-NARX神经网络预测模型确立：首先对水位信息利用箱形图法进行清洗，采用均值填充法进行插补；然后利用GRA法确定当前时刻、当前位置处的水位信息的主要影响因子；最后将主要影响因子输入NARX神经网络，确定NARX神经网络的训练算法、时间延迟、输入层隐含层神经元个数等，进行网络训练。基于GRA-NARX神经网络的泵站站前水位预测模型流程见图3。

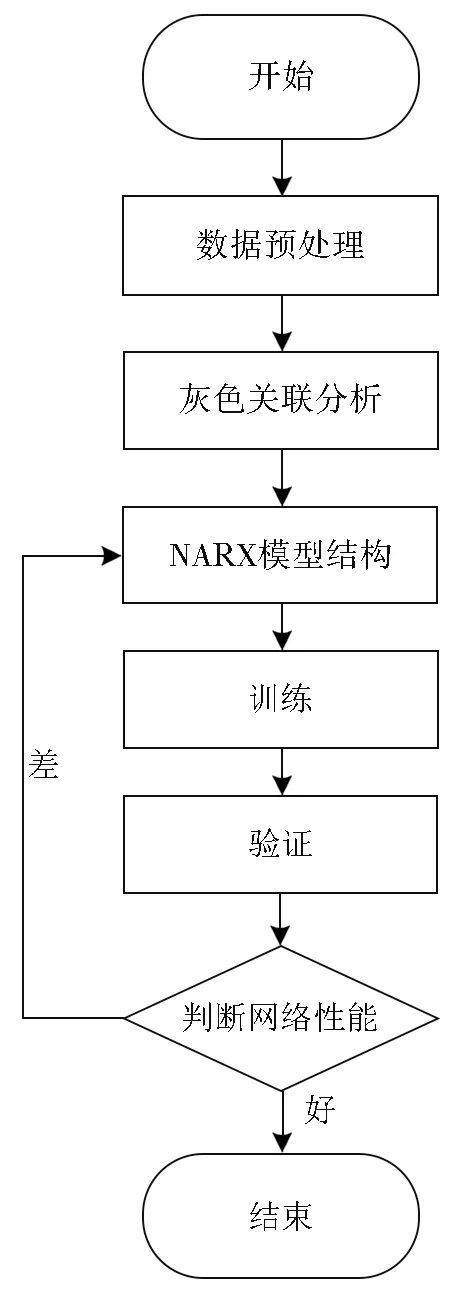
图3 基于灰色关联分析的NARX神经网络模型流程图Fig.3 Flow chart of NARX neural network model based on grey correlation analysis

2.4 预测结果评判标准

采用的评价标准为均方误差MSE、均方根误差RMSE和相关系数R。均方误差MSE和均方根误差RMSE反应的是预测值偏离实际值的程度，MSE和RMSE越小，表明预测效果越好。相关系数R反应的是预测值与实际值之间的相关程度，R越接近1相关程度越高。

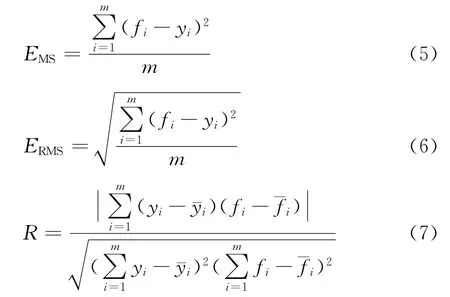
式中：EMS为MSE值；ERMS为RMSE值；y i和f i为水位实测值和水位预测值；ˉy i和ˉf i为水位实测平均值和水位预测平均值；m为数据列长度。

3 实例应用

3.1 区域概况与研究对象

密云水库调蓄工程于2015年5月投入运行，用以提高北京市水资源战略储备和城市供水率。该工程从颐和园内的团城湖取水，经9级泵站加压，输送至密云水库（图4），工程总长103 km，总扬程132.85 m。前6级泵站分别建在屯佃闸、柳林倒虹吸、埝头倒虹吸、兴寿倒虹吸、李史山节制闸和西台上跌水节制闸旁，串联京密引水渠输水至怀柔水库，不设调蓄工程，输水流量为20 m3／s。后3级泵站从郭家坞泵站到溪翁庄泵站，全长约31 km，包括8 km原京密引水渠道、22 km直径2.6 m的单排PCCP管道和约800 m的钢管管道，后3座加压泵站输水规模为10 m3／s。

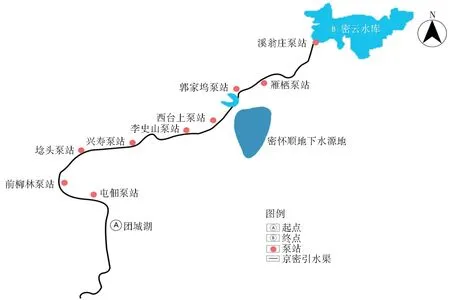
图4 密云水库调蓄工程示意图Fig.4 Schematic diagram of Miyun reservoir storage project

本文研究对象为整个复杂输水系统的第一级密云水库调蓄工程屯佃泵站，该站位于海淀区京密引水渠屯佃节制闸北侧，为渠道直接提升泵站，与屯佃节制闸配合运用，设计扬程1.71 m；距离上一个控制节点团城湖北闸8.1 km，沿程主要建筑物有安河扬水闸、农大分水闸、东干分水闸、北干分水闸、回民公墓扬水闸、五一分水闸、韩家川扬水闸、崔家窑分水闸和宏丰分水闸等；距离下一个控制节点前柳林泵站9.5 km，沿程经冷泉桥上扬水闸、太舟坞分水闸、三星庄分水闸、温泉倒虹吸、北安河扬水闸、前柳林倒虹吸等。水流条件十分复杂，水位预测难度较大。

3.2 水位监测数据清洗与插补

选取屯佃泵站2016年3月11日至2016年11月10日的2 868个站前水位实测值为监测数据，数据的时间间隔为2 h。按照2.2描述的步骤，利用箱形图法对数据进行清洗，其中，上四分位数为49.2，下四分位数为49.07，上限值为49.395，下限值为48.875，分布在上、下限值以外的点即为识别出的异常值，累计识别到20个异常值，见表1，再对异常数据和原有的空值利用均值填充法进行插补。

表1 监测数据中的异常值Tab.1 Outliers in monitoring data

3.3 水位信息的主要影响因子筛选、样本选择

考虑当前时刻的站前水位可能会受到上一个时刻的流量、上一时刻站前水位、上一时刻站后水位、上一时刻上一站闸前水位、上一时刻上一站闸后水位等因素的影响。以屯佃泵站当前时刻站前水位作为参考数列，比较数列为上一时刻（两小时前）的已知值，共包括5个：r1表示屯佃泵站上一时刻流量；r2表示屯佃泵站上一时刻站前水位；r3表示屯佃泵站上一时刻站后水位；r4表示团城湖末端上一时刻闸前水位；r5表示团城湖末端上一时刻闸后水位。选取清洗好的2 868个监测数据作为分析序列，对数据进行无量纲化处理，消除量纲与单位的差异，按照2.2描述的步骤进行计算，结果见表2。影响因子相关性排序从高到低依次为：屯佃泵站上一时刻站前水位；屯佃泵站上一时刻站后水位；屯佃泵站上一时刻流量；团城湖末端上一时刻闸后水位；团城湖末端上一时刻闸前水位。选择灰色关联度大于0.8的影响因子为主要影响因子。

表2 各影响因子与当前时刻泵前水位的灰色关联度Tab.2 Grey correlation grade between each influence factor and the water level in front of the pumping station at the current time

因此，将屯佃泵站上一时刻站前水位、站后水位这两个主要影响因子作为神经网络模型的输入量，以屯佃泵站当前时刻站前水位作为NARX神经网络模型训练阶段的输出量，待预测量为屯佃泵站下一时刻（两小时后）站前水位。

3.4 预测模型构建

3.4.1 GRA-NARX模型

将利用灰色关联分析筛选出的主要影响因子作为神经网络模型的输入量，屯佃泵站当前时刻站前水位作为输出量，由NARX神经网络模型对数据序列进行训练和检验。由于目前没有成熟的理论为输入数据的划分比例、神经元个数、隐含层和输出层的转移函数、最大迭代次数等提供依据，故根据经验及试错法，确定输入数据划分比例为70∶15∶15，它们依次是训练集、验证集和测试集，神经元个数为20，隐含层和输出层的转移函数分别为“tansig”和“purelin”，最大迭代次数1 000，学习率10－3，其他参数设置为默认值。

3.4.2 GRA-BP模型

为了比较不同的神经网络对相同输入的影响，GRA-BP神经网络的输入因子与输出因子、输入数据划分比例、隐含层神经元个数、隐含层和输出层的转移函数等均与GRA-NARX神经网络一致，不同的是GRA-NARX神经网络的输出会反馈到下一个时刻的输入。

3.4.3 NARX模型

NARX模型的输入因子为屯佃泵站上一时刻流量、屯佃泵站上一时刻站前水位、屯佃泵站上一时刻站后水位、团城湖末端上一时刻闸前水位、团城湖末端上一时刻闸后水位，输出因子为屯佃泵站当前时刻站前水位，输入数据划分比例、隐含层神经元个数、隐含层和输出层的转移函数等均与GRANARX神经网络一致。

3.4.4 训练算法

采用3种训练算法对GRA-NARX模型、GRABP模型和NARX模型进行研究。第一种训练算法是LM，它收敛速度快，且收敛速度稳定，广泛应用于神经网络的时间序列预测；第二种训练算法是BR（bayesian regularization），一般情况下，LM算法速度快，而BR算法在复杂问题上效果更好；第三种训练算法是SCG（scaled conjugate gradient），它是一种用于解决大型线性方程系统问题的迭代算法，收敛速度介于前两者之间。

3.5 结果分析

表3为3种训练算法的GRA-NARX模型和NARX模型不同时间延迟的预测结果。由表3可知：GRA-NARX-BR模型（训练算法为BR的GRANARX神经网络）比NARX模型的预测结果好；不同的时间延迟下，均是GRA-NARX-BR模型下的相关系数最高，均方误差和均方根误差最小；在GRA-NARX-BR模型中，随时间延迟的增加，相关系数基本相当，均方误差和均方根误差越来越小，训练时长越来越长。

表3 3种训练算法的GRA-NARX模型和NARX模型不同时间延迟的预测结果Tab.3 Prediction of GRA-NARX model and NARX model of three training algorithms with different time delays

图5为GRA-NARX模型和GRA-BP模型在不同训练算法下实测值与预测值散点图。由于GRA-NARX模型的训练时长会随着时间延迟的增加而增加，设置时间延迟为6，与GRA-BP模型对比。当训练算法为BR时，GRA-NARX模型的R值为0.986 62，GRA-BP模型的R值为0.956 03；当训练算法为LM时，GRA-NARX模型的R值为0.978 67，GRA-BP模型的R值为0.970 02；当训练算法为SCG时，GRA-NARX模型的R值为0.969 13，GRA-BP模型的R值为0.946 71。由此看，3种训练算法下的GRA-NARX模型，相关系数均优于GRA-BP模型，GRA-NARX-BR最优。

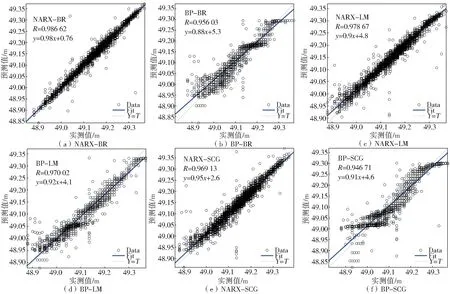
图5 不同训练算法的2种神经网络实测值与预测值散点图Fig.5 Scatter plots of measured and predicted values for two neural networks with different training algorithms

表4为GRA-NARX模型和GRA-BP模型在不同训练算法下的均方误差和均方根误差，GRANARX模型的时间延迟设置为6。结果显示：当训练算法为BR时，GRA-NARX模型的均方误差为1.348 4×10－4，均方根误差为0.011 61，GRA-BP模型的均方误差为8.741 6×10－4，均方根误差为0.029 57；当训练算法为LM时，GRA-NARX模型的均方误差为3.855 1×10－4，均方根误差为0.019 63，GRA-BP模型的均方误差为9.584 1×10－4，均方根误差为0.030 96；当训练算法为SCG时，GRA-NARX模型的均方误差为3.922×10－4，均方根误差为0.019 80，GRA-BP模型的均方误差为9.978 1×10－4，均方根误差为0.031 59。以上分析说明，GRA-NARX模型的均方误差和均方根误差比GRA-BP模型的均方误差和均方根误差都小，GRA-NARX-BR模型的均方误差和均方根误差最小。

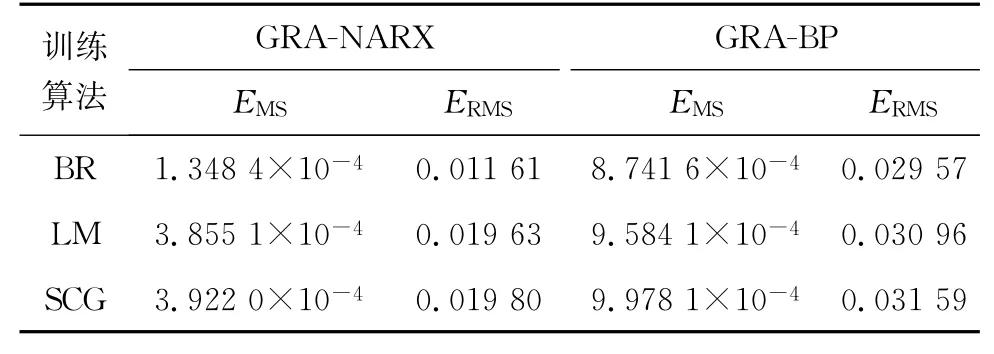
表4 2种模型不同训练算法的均方误差和均方根误差Tab.4 Mean square errors and root mean square errors for two models of different training algorithms

4 结 论

本文利用灰色关联分析（GRA）和NARX神经网络的各自优势，构建了一种新的基于GRANARX神经网络的泵站站前水位预测模型，利用BR、LM、SCG等3种训练算法及不同时间延迟分别给出了密云水库调蓄工程屯佃泵站站前水位的2 h预测结果，将模型预测结果与NARX模型和GRA-BP模型进行比较，并评估了3种训练算法及不同时间延迟对预测精度的影响，得到如下结论：

基于GRA-NARX神经网络的泵站站前水位预测模型模型可降低预测的复杂度并保证预测的精度，具有广泛的适用性，能够很好地对复杂的多输入、多输出系统进行逼近模拟，模型适用调水工程的数据情况，相关系数最高达0.986 62，均方根误差最小为0.008 6 m。

3种训练算法下的GRA-NARX模型中，训练算法为BR的GRA-NARX神经网络（GRANARX-BR模型）能够高精度预测屯佃泵站站前水位，表现最好，相关系数最高，均方误差最小，预测精度高于NARX模型和GRA-BP模型，所提模型可作为其他泵站站前水位预测替代模型。

在GRA-NARX-BR模型中，随着时间延迟的增加，相关系数基本相当，均方误差越来越小，训练时长越来越长。

由于影响密云水库调蓄工程梯级泵站水位变化的因素比较多，今后将进一步考虑模型输入的复杂性和多样性对预测结果的影响。此外，如何更科学的选取模型参数也是下一步需要研究的工作。