基于生存分析的学区衔接路网交通拥塞持续时长研究
2022-11-10胡立伟赵雪亭张成杰吕一帆雷国庆
胡立伟,刘 凡,赵雪亭,张成杰,吕一帆,薛 宇,雷国庆
(昆明理工大学 交通工程学院,云南 昆明 650500)
0 引 言
近年来,城市交通出行需求和基础设施建设速度间的矛盾较为突出,交通拥塞已成为城市交通运输中最常见的问题之一.国内外每年因就学产生的接送行为导致各城市学校门口及周边区域路网交通拥塞现象严重,产生大量的经济损失,且造成能源浪费以及环境污染.为有效减少拥塞的危害,国内外学者都致力于缓解以及消除交通拥塞的研究与实践中.
陈亮等[1]建立基于元胞自动机(Cellular Automaton, CA)的多车道交织区离散模型,对交织区拥塞现象开展仿真模拟并分析拥塞形成机制;Kong等[2]通过分析浮动车轨迹数据,采用粒子群模糊综合评价优化算法对城市交通拥塞进行识别和预测;向红艳等[3]利用交通事件具有相似性的特征,以历史交通事件的持续时间为基础,通过搜索与当前交通事件最相近的历史事件集合进行持续预测,可最大程度利用历史信息,并提高预测精度;张波等[4]以北京首都国际机场为研究对象,将航空因素引入到长短时记忆网络模型(Long Short Term Memory, LSTM),提升了机场路面交通拥塞延时指数的预测效果;吕鲜等[5]提出基于长短期记忆模型的交通拥塞预测方法,具有较高的预测准确度和鲁棒性;顾金刚等[6]提出以排队时间指数为指标对信号控制路口拥塞状况进行评价;周辉宇等[7]提出了一个新的基于时空关联规则的交通拥塞传导预测模型,揭示了交通拥塞的时空传导模式;曾筠程等[8]提出了一种针对城市快速路的基于有向图卷积神经网络的交通预测与拥塞管控方法,实现拥塞的主动管控.
现有的城市交通拥塞研究大多关注交通拥塞预测方法及模型、拥塞管控策略以及拥塞评价模型等方面,而在交通拥塞持续时长方面研究较少.周映雪等[9]以北京交通为例,构建了基于风险的交通拥塞持续时间模型,分析了不同时段的交通拥塞持续时间特征;熊励等[10]构建了拥塞预测模型以及拥塞持续时间模型,以上海快速路交通为例进行验证;Liu等[11]基于多元线性回归构建交通拥挤预测模型,又利用Kaplan-Meyer模型构建了交通拥挤持续时间模型,模型拟合度较好.
目前国内外学者大多是对学校周围交通组织进行优化仿真,而针对学区衔接路网交通状态的研究较少.本文依托昆明市五华区小学衔接路网的交通拥塞数据,构建单因素的Kaplan-Meyer回归模型,用Log-Rank法进行显著性检验,并构建多因素的Cox回归模型(又称“比例风险回归模型”),综合评价交通拥塞持续时长的显著影响因素,计算交通拥塞持续时长的风险函数,在此基础上构建交通拥塞持续时长生存率的列线图预测模型,对模型的预测精度进行评价,并对模型进行外部验证以评估其预测价值.
1 基于SAM的学区衔接路网交通拥塞持续时长列线图预测模型构建
1.1 模型构建思路
本文利用生存分析法(Survival Analysis Method,SAM)对学区衔接路网交通拥塞持续时长进行分析,最终得到多因素拥塞持续时长综合评价结果.根据影响因素分析结果,绘制列线图构建预测模型,用于预测交通拥塞持续时长生存率.其评价具体流程如图1所示,具体步骤如下所述:
1)基于现有对交通拥塞持续时长的研究成果及相关学区衔接路网交通拥塞数据,初步确定交通拥塞持续时长的关键影响因素;
2)构建单因素的Kaplan-Meier回归模型,得到累计生存函数和风险函数曲线;
3)用Log-Rank法检验影响因素的显著性,分析单一影响因素下学区衔接路网交通拥塞持续时长的分布特性;
4)构建多因素的Cox回归模型.确定交通拥塞持续时长的风险函数,得到交通拥塞持续时长的多因素持续时长综合评价,提取表征学区衔接路网交通拥塞的重要特征参数;
5)构建交通拥塞持续时长生存率的列线图预测模型,采用受试者工作特性曲线(Receiver Operating Characteristic Curve,ROC)下面积(Area Under Curve, AUC)和校准曲线对模型的预测精度进行评价,并对该模型进行外部验证以评估该模型的预测价值.
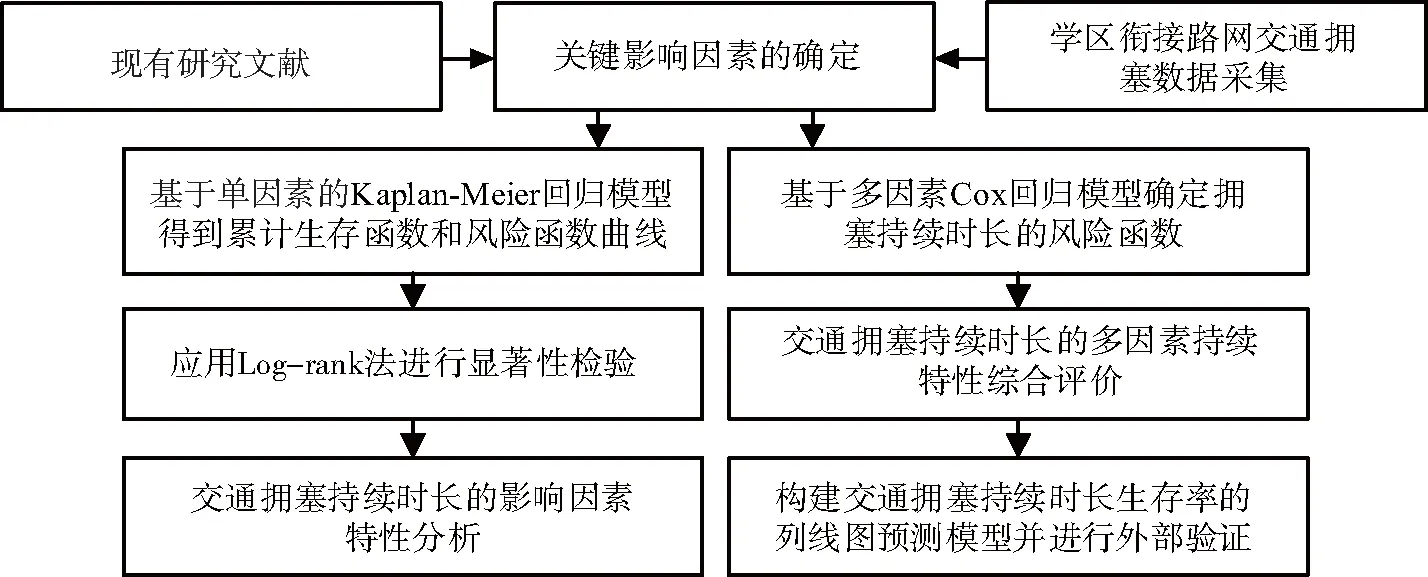
图1 交通拥塞持续时长预测模型构建流程Fig.1 Construction process of traffic congestion duration prediction model
1.2 研究方法
生存分析法近年来逐步被运用到城市交通领域的研究中[12].运用Kaplan-Meier法来进行单一影响因素特性分析;运用Cox回归模型进行多因素分析,分析各影响因素对拥塞影响的程度.
将列线图应用于交通拥塞持续时长的研究中,列线图可根据Cox回归模型中对各影响因素对应变量的贡献程度,给出各影响因素的影响评分,再计算某个体的总得分,由此得到个体的预测值[13].
1.3 建模过程
1.3.1 单因素的Kaplan-Meier回归建模
交通拥塞生存函数S(t)是指从交通拥塞开始到时间t时拥塞仍然存在的样本的概率分布,也称为累计生存函数,表示如下:
(1)
(2)
式中:F(t)表示分布函数;P表示概率;T表示交通拥塞持续时长,min;f(x)表示T取值为时刻x的概率密度.当生存概率较低时,生存曲线S(t)较陡峭;当生存概率较高时,生存曲线S(t)较平坦.
交通拥塞风险函数h(t)是指交通拥塞在时刻t发生后没有消失,但在极小时间段Δt内消失的概率,也叫条件生存概率,表示如下:
(3)
由风险函数积分可得到累计风险函数曲线,其位置越高,表示在时间内交通拥塞结束的概率越高.
1.3.2 多因素的Cox回归建模
Cox回归模型不直接考察生存函数S(t)与协变量的关系,而是用风险函数h(t)作为因变量,并假定:
h(t,x)=h0(t)exp(β1x1+β2x2+…+βixi)
(4)
式中:t是交通拥塞持续时长,min;x=(x1,x2,…,xi)是影响因素组成的向量;β=(β1,β2,…,βi)是影响因素对应的回归系数;h(t,x)是风险函数;h0(t)是基础风险函数.把式(4)取对数,得到Cox回归的线性模型如式(5)所示:
(5)
根据生存函数S(t,x)与风险函数h(t,x)的关系可以推导出:
(6)
协变量函数exp(β1x1+β2x2+…+βixi)中,βi表示当其他协变量不变时,xi每变化一个单位,风险率的自然对数变化βi个单位.βi与风险函数h(t,x)之间的关系如下:
若βi>0,h(t,x)>1,该因素为危险因素;若βi<0,h(t,x)<1,该因素为保护因素;若βi=0,h(t,x)=1,该因素为无关因素[14].
1.3.3 列线图预测建模
利用R4.1.0软件及衰退建模策略程序包建立列线图预测模型.采用ROC曲线下面积(AUC)和校准曲线评估列线图模型的准确度和区分度.预测曲线与实际观察曲线吻合度越高说明模型预测准确度越好;ROC曲线下面积AUC代表模型预测效能,AUC越接近1说明模型的预测效能越好.另外用一组数据作为验证组来进行外部验证,以评估该模型的预测价值.
2 数据来源与影响因素的确定
以昆明市五华区的路网为研究对象,利用网络数据爬虫,记录了一个月内路网高峰时段的主要交通拥塞道路并进行标记,筛选出位于小学衔接路网的主要道路作为本文的研究对象.从处于小学衔接路网的主要道路中选取10个典型断面展开调查,调查时间为2021年昆明市五华区5所小学暑假放假前2周和后2周(共4周),剔除重复、缺失和异常的数据,共生成 1 475 组完整的交通拥塞数据集.
影响小学衔接路网交通拥塞持续时长的因素可分为时间因素、驾驶人因素、车辆因素、道路因素、环境因素以及其他相关因素等.每组数据包含交通拥塞持续时长和可能影响拥塞持续时长的21个影响因素.初步确定样本数据的交通拥塞影响因素并对这21个变量进行赋值,如表2所述,选取的关键影响因素变量分析如表3所述.
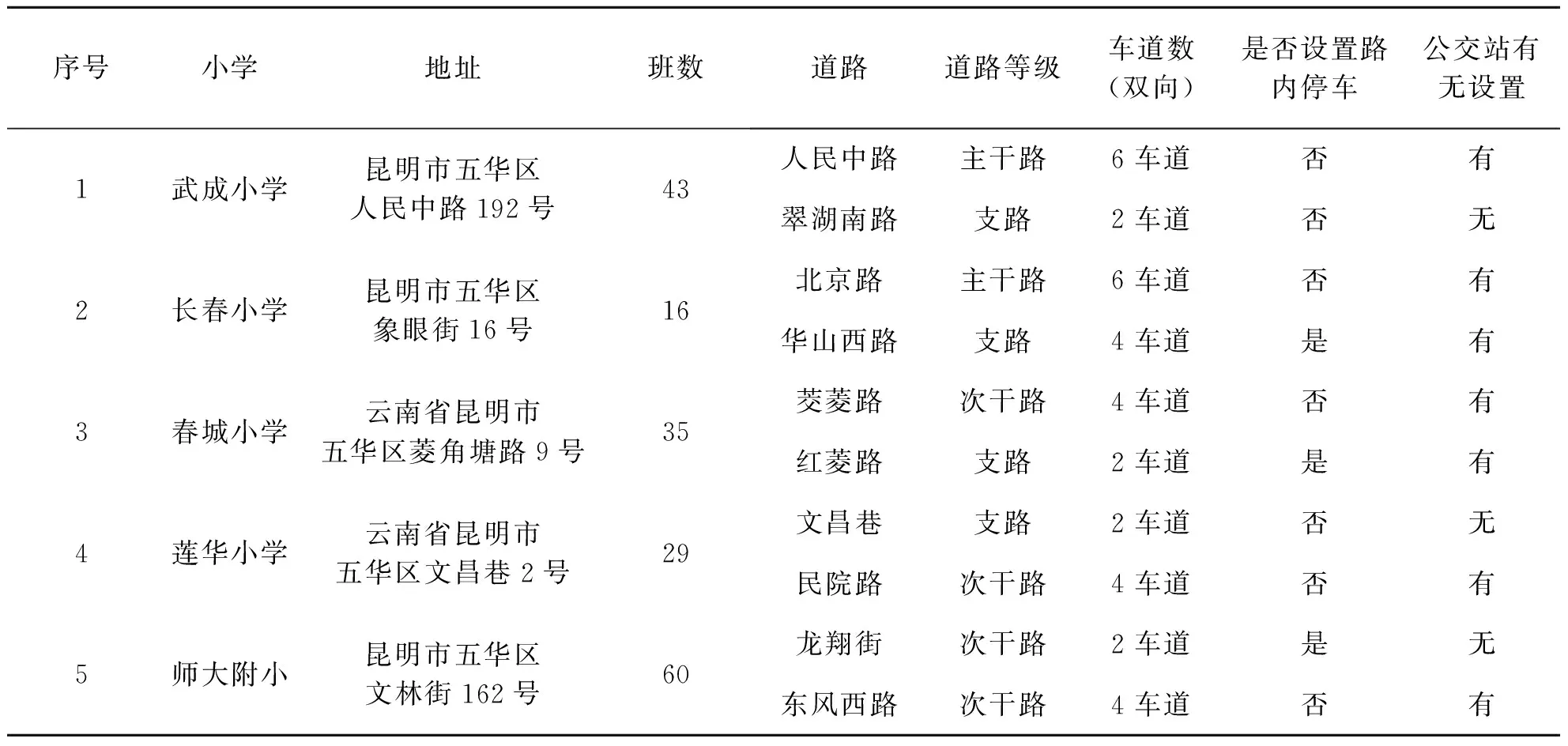
表1 小学及主要道路的基本信息

图2 小学及主要道路分布Fig.2 Distribution of primary schools and main roads
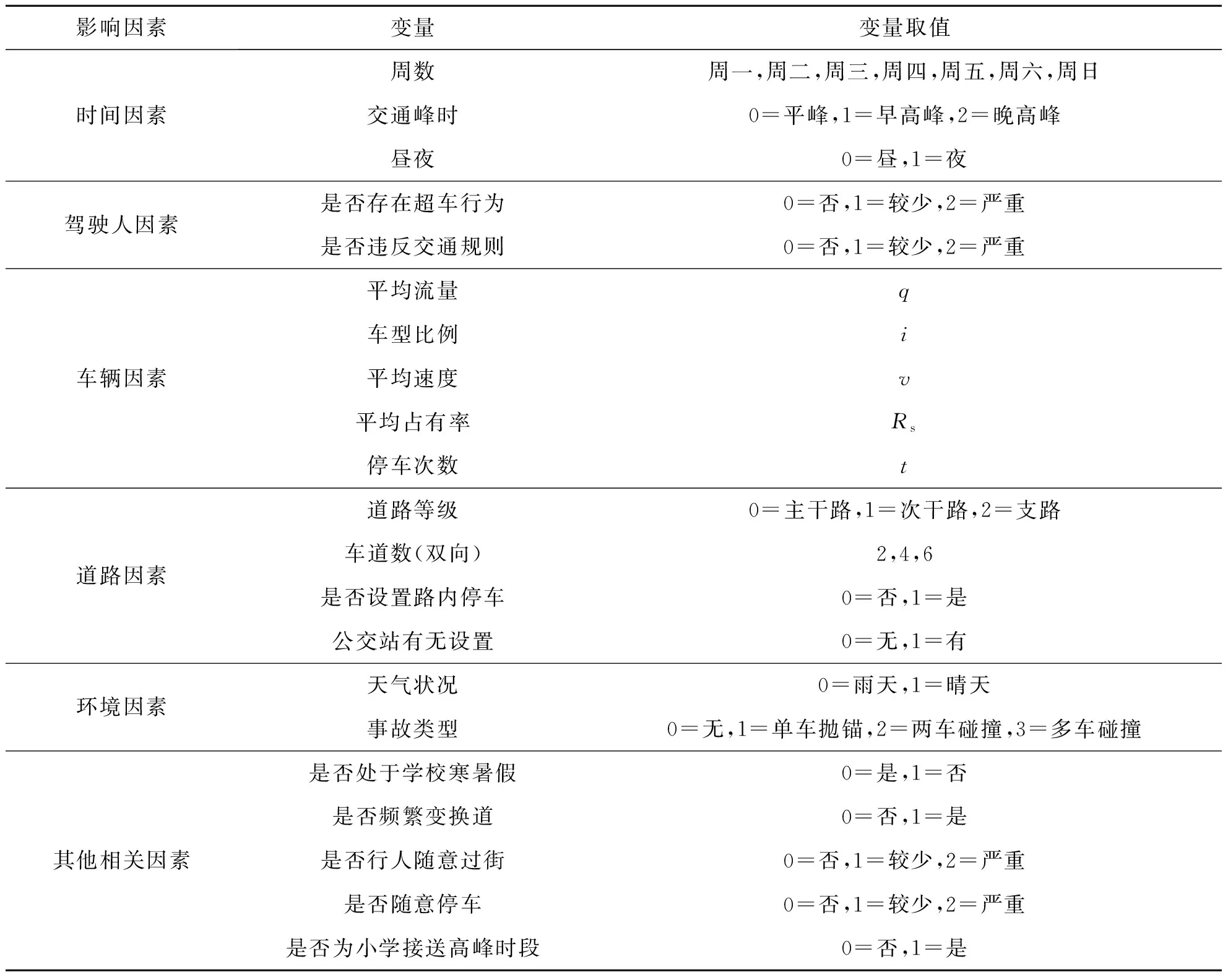
表2 交通拥塞影响因素及其变量赋值表
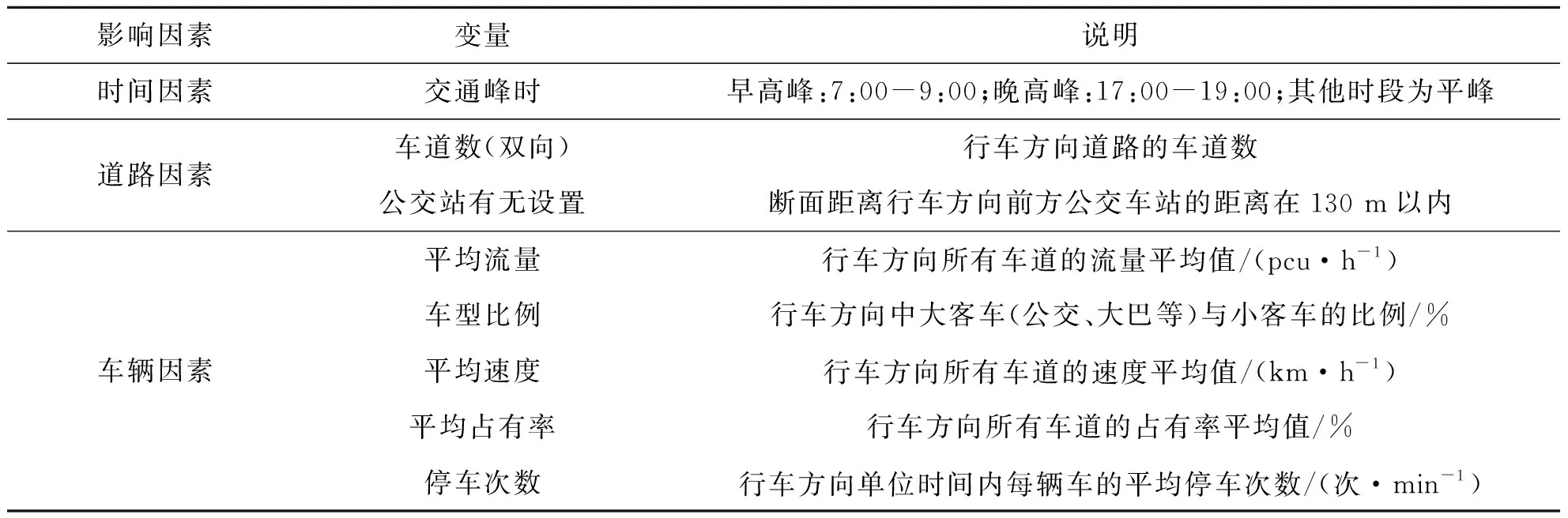
表3 关键影响因素分析
3 模型验证
3.1 基于Kaplan-Meyer的影响因素特性分析
3.1.1 时间分布特性
运用SPSS 26.0软件绘制交通拥塞持续时长在时间相关影响因素作用下的累计生存函数和累积风险函数曲线如图3、图4所示.时间影响因素特性分析如表4所示.Log-Rank特征值P<0.05时,说明该影响因素对拥塞持续时长有显著影响.
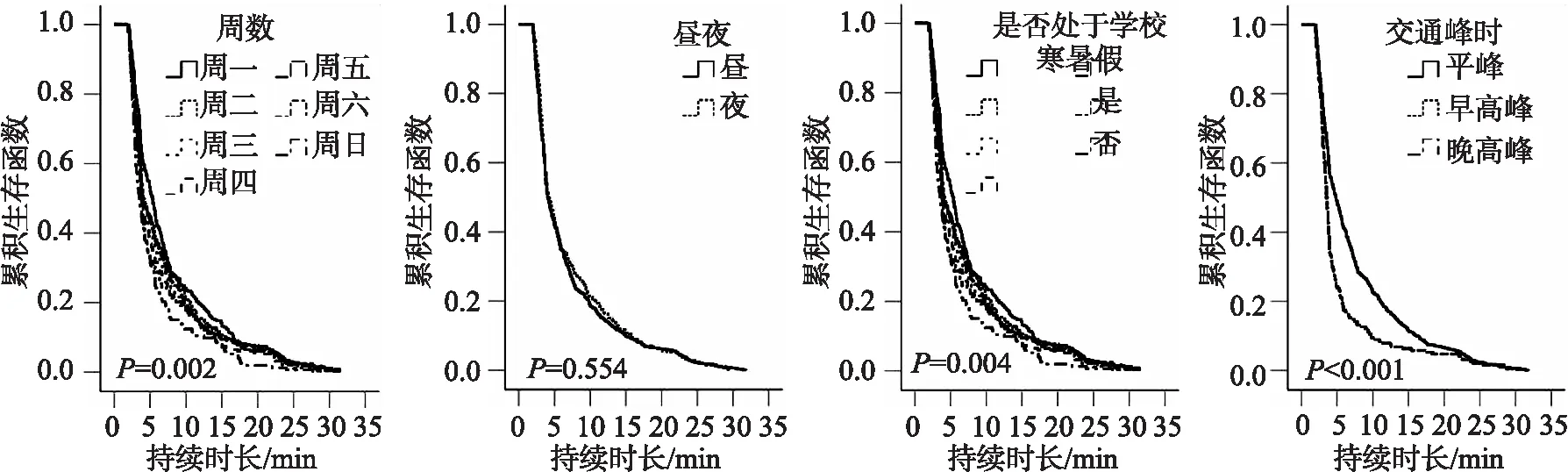
(a) 周数 (b) 昼夜 (c) 是否处于学校寒暑假 (d) 交通峰时图3 交通拥塞持续时长的累计生存函数Fig.3 Cumulative survival function of the duration of traffic congestion
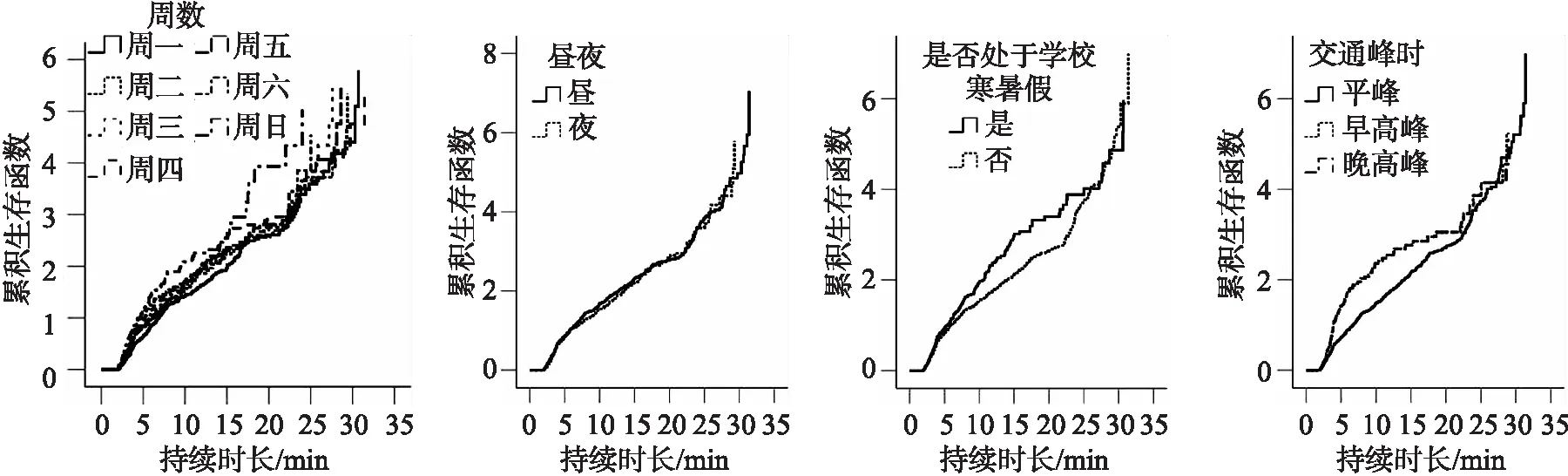
(a) 周数 (b) 昼夜 (c) 是否处于学校寒暑假 (d) 交通峰时图4 交通拥塞持续时长的累计风险函数Fig.4 Cumulative risk function of the duration of traffic congestion
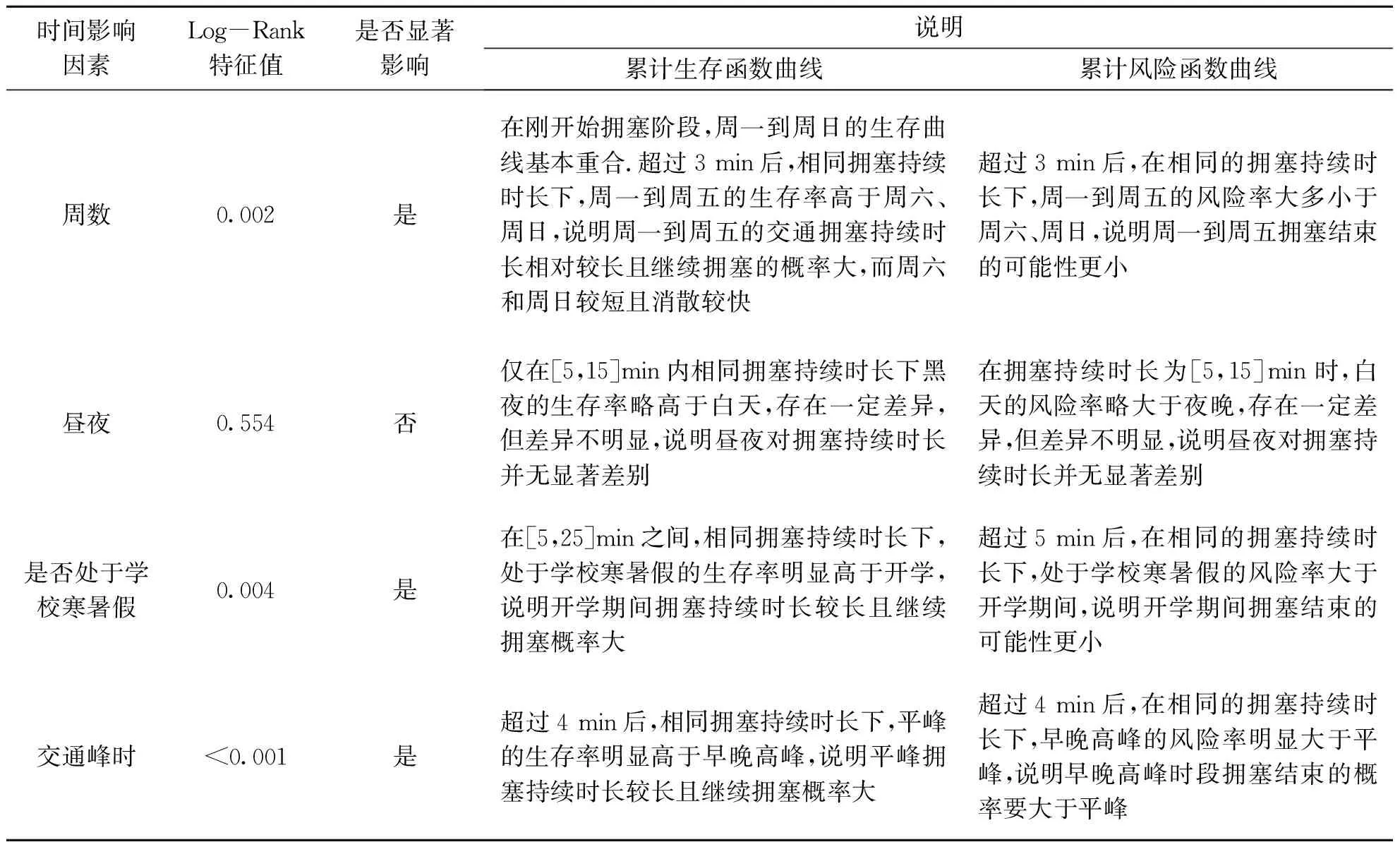
表4 时间影响因素特性分析
3.1.2 空间分布特性
空间相关影响因素作用下的累计生存函数和累计风险函数曲线如图5、图6所示.空间影响因素特性分析如表5所示.
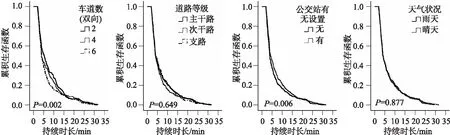
(a) 车道数(双向) (b) 道路等级 (c) 公交站有无设置 (d) 天气状况图5 交通拥塞持续时长的累计生存函数Fig.5 Cumulative survival function of the duration of traffic congestion
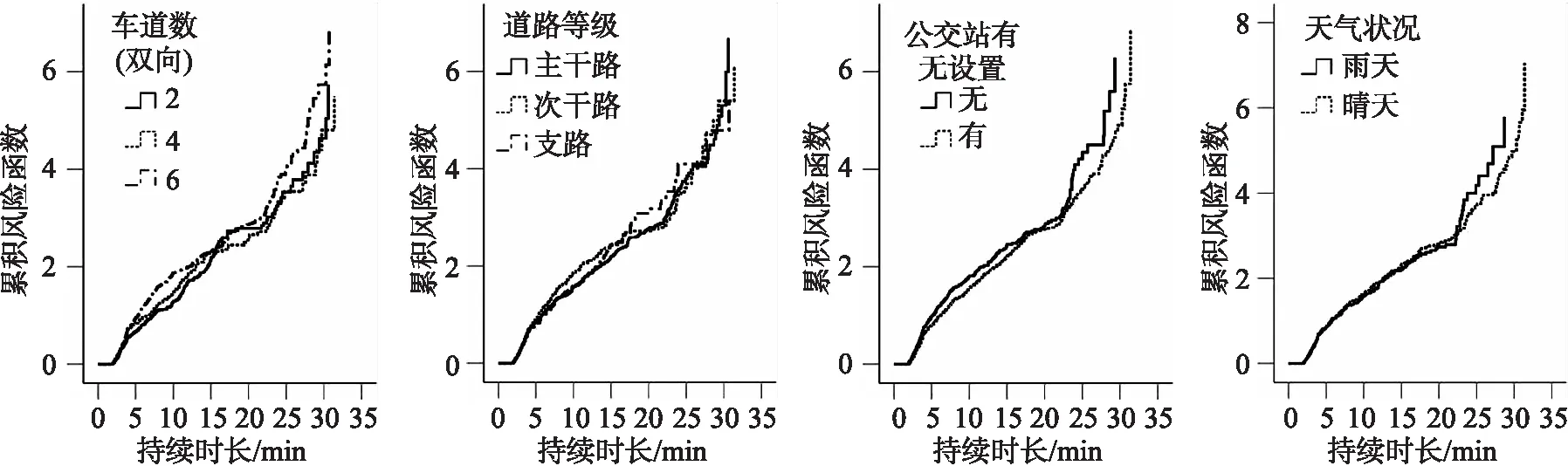
(a) 车道数(双向) (b) 道路等级 (c) 公交站有无设置 (d) 天气状况图6 交通拥塞持续时长的累计风险函数Fig.6 Cumulative risk function of the duration of traffic congestion
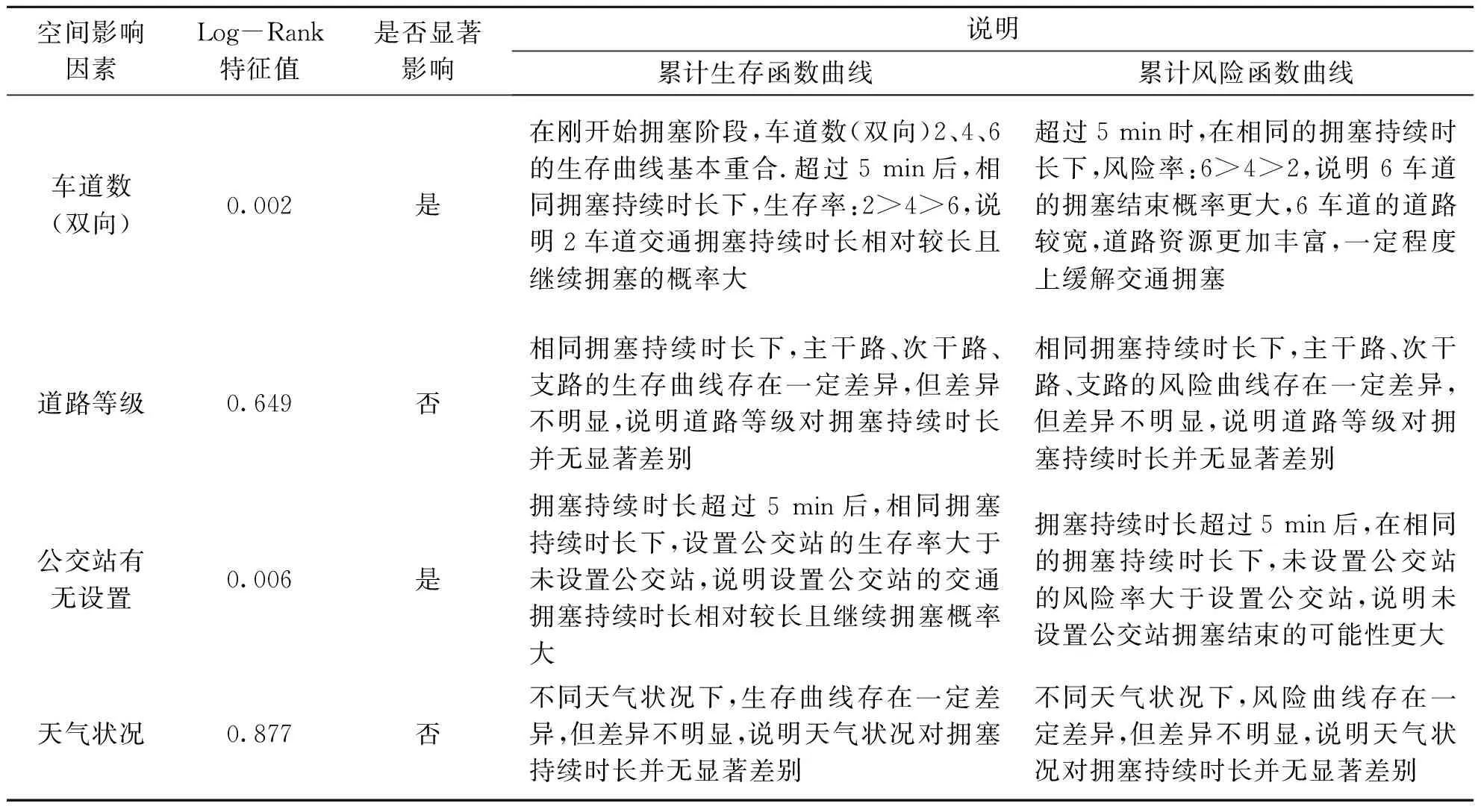
表5 空间影响因素特性分析
3.2 基于Cox回归的多因素持续特性综合评价
通过上述的Kaplan-Meyer分析得到昼夜、道路等级、天气状况3个因素无显著影响,因此对其余的18个影响因素进行Cox回归分析.得到周数、交通峰时、平均速度、车道数(双向)、公交站有无设置、事故类型、是否处于学校寒暑假、是否频繁变换道共计8个影响因素在模型中,即这些影响因素对拥塞持续时长有显著影响.而不在方程中的因素有是否存在超车行为、是否违反交通规则、平均流量、车型比例、平均占有率、停车次数、是否设置路内停车、是否行人随意过街、是否随意停车、是否为小学接送高峰时段共10个,它们的Log-Rank特征值P均大于0.05.表6为模型中的影响因素的参数估计.
表6中,β为对应影响因素的回归系数,SE为系数标准误差,Wald是检验系数与0有无显著性差异,exp(β)为胜算比值.根据表6,交通拥塞持续时长的风险函数为:
h(t,x)=h0(t)exp(0.050x1+0.205x2+0.493x3+0.310x4-1.956x5-0.087x6-0.147x7-1.844x8)
(7)
对分类变量“周数和事故类型”,以“周一”和“无事故”作为参考基准,采用Cox回归模型的分类变量模块对其进行筛选,各参数估计的结果如表7所示.

表6 Cox回归模型的参数估计表

续表6
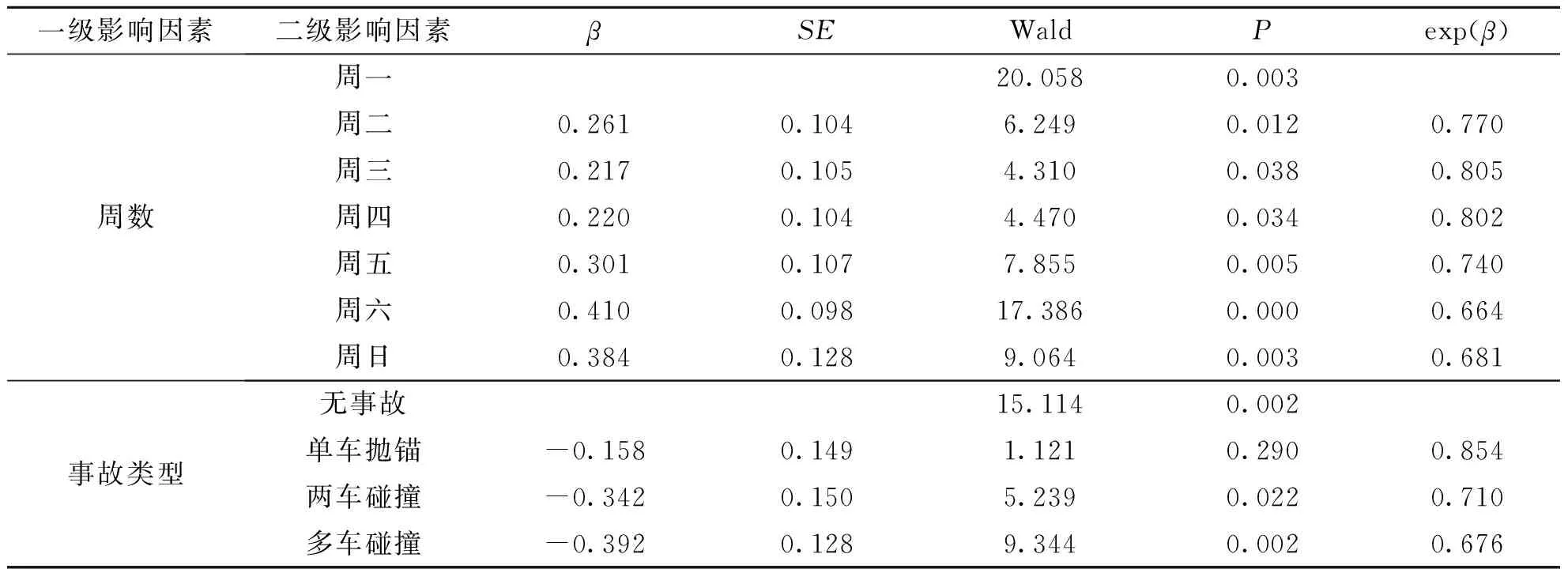
表7 周数及事故类型Cox回归模型参数估计表
由表5~表7可以看出,危险因素有周数、交通峰时、平均速度、车道数(双向).
周一的持续时长最长,其他周数的拥塞持续时长从短至长分别是周六、周日、周五、周二、周四及周三;早晚高峰时段拥塞结束的概率是平峰时段的1.228倍;当平均速度增大,则风险率增大,因此拥塞结束概率会增大,持续时长减小;2车道比4车道风险率低,4车道比6车道风险率低,因此2车道的拥塞持续时长更长.车道数(双向)每增加一单位,拥塞结束概率增加16.4%.
保护因素有公交站有无设置、事故类型、是否处于学校寒暑假、是否频繁变换道.
有公交站时风险率更小,拥塞结束的可能性减少12.4%,拥塞持续时长更长;无事故发生时的交通拥塞持续时长最短,其他事故类型的拥塞持续时长从短至长分别为单车抛锚、两车碰撞、多车碰撞;开学后风险率更小,拥塞结束的可能性减少13.6%,拥塞持续时长更长;当车辆存在频繁变换道时风险率更小,拥塞结束的可能性减少11.8%,拥塞持续时长更长.
4 列线图预测模型的构建与验证
4.1.1 构建预测交通拥塞持续时长生存率的列线图模型
将Cox回归分析得出的8个显著影响因素(周数、交通峰时、平均速度、车道数(双向)、公交站有无设置、事故类型、是否处于学校寒暑假、是否频繁变换道)纳入列线图的绘制,构建交通拥塞持续时长生存率的列线图预测模型,如图7所示.
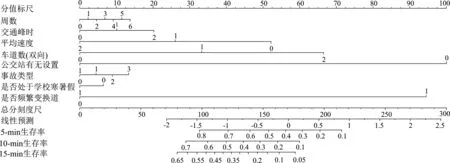
图7 列线图预测模型Fig.7 Nomogram prediction model
通过列线图可得到各影响因素的不同分类对应分值标尺上的积分,各积分的总和记为总分,在总分标尺上垂直向下对应,即可得到交通拥塞持续时长为 5 min、10 min、15 min 时的生存率.
列线图预测交通拥塞持续时长为 5 min、10 min、15 min 的AUC分别为0.677、0.721和0.683.绘制ROC曲线,表示该预测模型具有良好的区分度,如图8所示.绘制 5 min、10 min、15 min 后交通拥塞持续时长生存率的校准曲线,显示预测生存率与实际生存率具有较好的符合度,如图9所示.因此这个模型具有良好的预测精度.
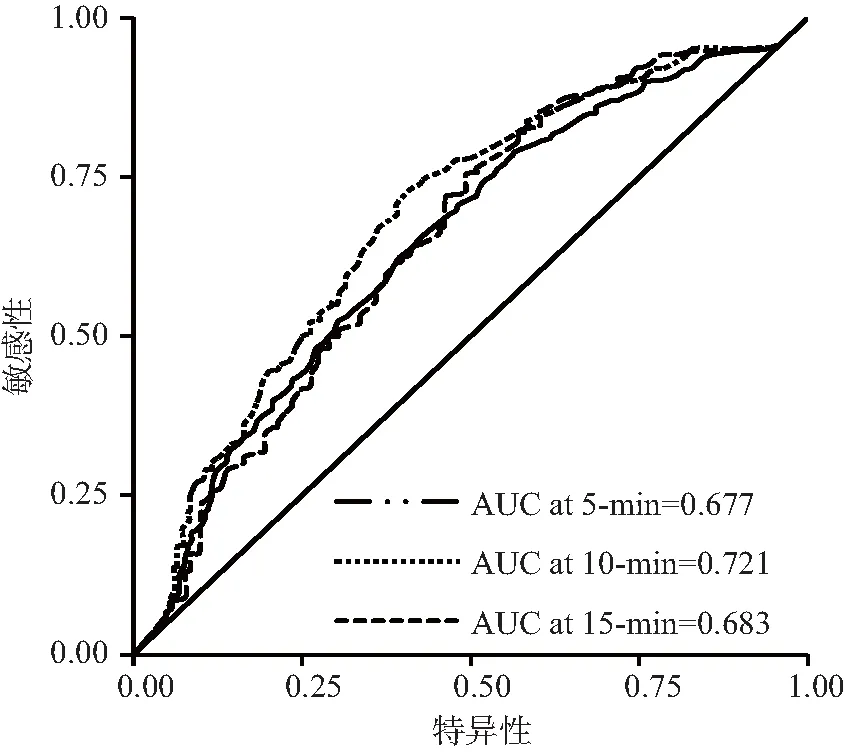
图8 ROC曲线Fig.8 ROC curve
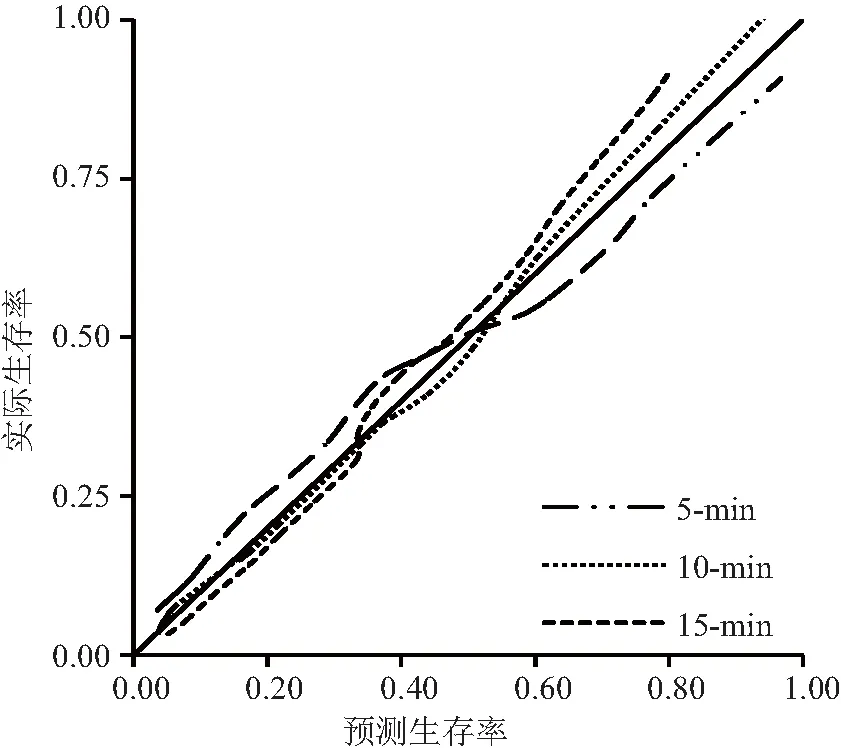
图9 校准曲线Fig.9 The calibration curve
4.1.2 列线图预测模型的外部验证
将另外的516组数据组成验证组进行外部验证.对该数据进行生存分析,应用Log-Rank检验法—Kaplan-Meier法对影响因素进行显著性检验,应用Cox回归筛选出显著影响因素,最终得到影响因素的参数估计如表8所示.
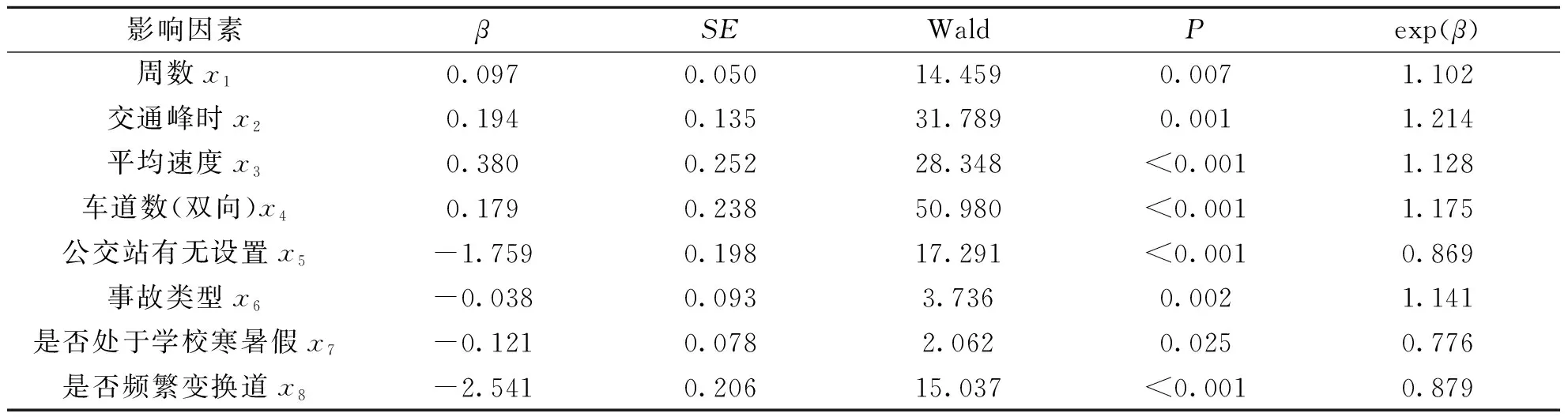
表8 外部验证组影响因素的参数估计表
对列线图预测模型进行外部验证,绘制ROC曲线如图10所示,发现列线图模型预测交通拥塞持续时长为 5 min、10 min、15 min 生存率的AUC分别为0.754、0.836、0.802(AUC的取值范围为[0.5,1.0],AUC越接近1.0,检测方法真实性越高),表明该列线图预测模型有较高的预测价值.
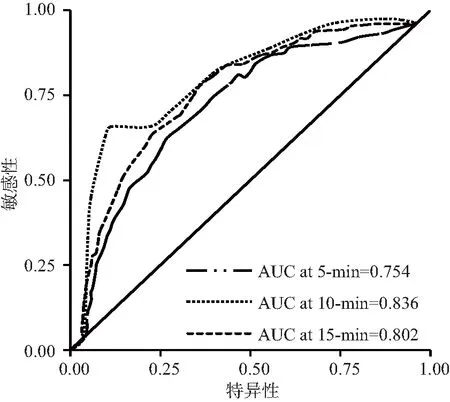
图10 外部验证的ROC曲线Fig.10 Externally validated ROC curve
5 结 论
研究学区衔接路网交通拥塞的影响因素,采用生存分析法对数据进行分析,运用列线图方法构建拥塞持续时长预测模型,得到以下结论:
1) 以昆明市五华区小学衔接路网为研究对象,应用Log-Rank检验法—Kaplan-Meier法对可能影响拥塞持续时长的8个时空相关影响因素进行显著性检验,得到昼夜、道路等级、天气状况3个为无关影响因素.
2) 应用Cox回归对剩余的18个影响因素进行分析,筛选出的8个显著影响因素分别为:周数、交通峰时、平均速度、车道数(双向)、公交站有无设置、事故类型、是否处于学校寒暑假、是否频繁变换道;早晚高峰时段拥塞结束的概率是平峰时段的1.228倍;车道数(双向)每增加一单位,拥塞结束概率增加16.4%;开学后、有公交站、车辆存在频繁变换道拥塞结束的可能性减少13.6%、12.4%、11.8%.
3) 本文将列线图用于交通拥塞的预测当中,AUC值和校准曲线表明该模型的预测精度良好,能有效预测交通拥塞情况,外部验证结果显示该模型有较高的预测价值.今后的研究中应尽可能获取更加全面的数据以提高研究的可信度,并在其他城市道路中进一步验证模型的有效性.
