基于粒描述的模糊关联规则获取
2022-11-10智慧来马一凡
智慧来,马一凡
(河南理工大学 计算机科学与技术学院,河南 焦作 454003)
0 引 言
众所周知,关联规则通常用于描述数据表中的特定依赖项[1-2]. 在给定表中所有正确或有效的规则中,有必要删除那些冗余的规则. 因此,快速高效地找到一个最小的规则集基是一个有趣而重要的问题,从这个规则集可以依据给定的推理方式从给定数据表中得到所有的规则. Godin等[3]对于具有二进制属性的数据表研究了无冗余规则的获取. 对于具有模糊属性的数据表,Bělohlávek等[4]讨论了获取非冗余规则的思路. 此外,Vychodil[5]还研究了描述分级属性间依赖关系的非冗余If-Then规则集,并证明了一些有用的性质.
形式概念分析是一种有效的数据挖掘工具,基于概念格的规则获取是一种有效的方法[6]. 为了获得非冗余规则,现有的通常的做法是基于属性约简,也就是寻找概念的最小产生子[7],并建立差别矩阵[8-9]. 然而,建立概念格与计算属性约简都已被证明是NP难问题.
粒计算的基本认知单位是粒,通过多粒度分析解决现在社会中的复杂问题[10-11]. 对粒进行恰当的刻画是利用粒计算思想解决问题的前提,同时为实现可解释人工智能提供了可能的途径[12]. Zhi和Li[13]提出了基于形式概念分析的粒描述方法,实质是借助于概念的内涵来刻画粒. 此外,从刻画粒的独有属性的角度出发,智慧来和李金海[14]又提出了一种粒描述方式. 从微观的角度,Li和Liu[15]研究了可定义粒的组成与性质. 苗夺谦等[16]在研究等价关系运算基础上提出了刻画粒的形式化方法.
从数学的角度,规则一定蕴含在特定的信息粒中. 换言之,若能够获取粒的描述,则可以得到蕴含在粒中的规则[17]. 进一步,若能够获取粒的最简描述,则可以获得无冗余的规则. 为了更加有效地获取无冗余的模糊规则,本文用模糊形式背景刻画原始数据,提出一种基于粒描述的模糊规则获取方法.
1 基础知识
模糊概念格是模糊集与形式概念分析两者有机结合产生的数学模型. 在文献[18]与[19]中有详细论述,这里只列出最基本的概念.
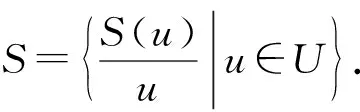
对于两个模糊集S1与S2,称S1包含于S2当且仅当若对于任意的u∈U有S1(u)≤S2(u),并记做S1⊆S2.此外,定义S1,S2上交与并的运算如下:
一个模糊形式背景可以表示为一个四元组K=(X,Y,I,L),其中包括对象集X、属性集Y、真值集L,以及建立在真值集L的模糊二元关系I.
对于A∈LX和B∈LY,定义算子↑:LX→LY和↓:LY→LX如下:
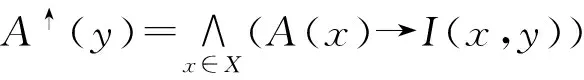
其中,对于a,b∈L,a→b=min(1-a+b,1).
若满足A↑=B且B↓=A,则称(A,B)为一个模糊概念. K中的所有模糊概念依据父子关系构成的完备格称为模糊概念格,记为L(K).
例1一个由五个对象构成的模糊形式背景K=(X,Y,I,L)如表1所示,其中L={0,0.5,1}. 图1为K的模糊概念格L(K).

表1 模糊形式背景K=(X,Y,I,L)
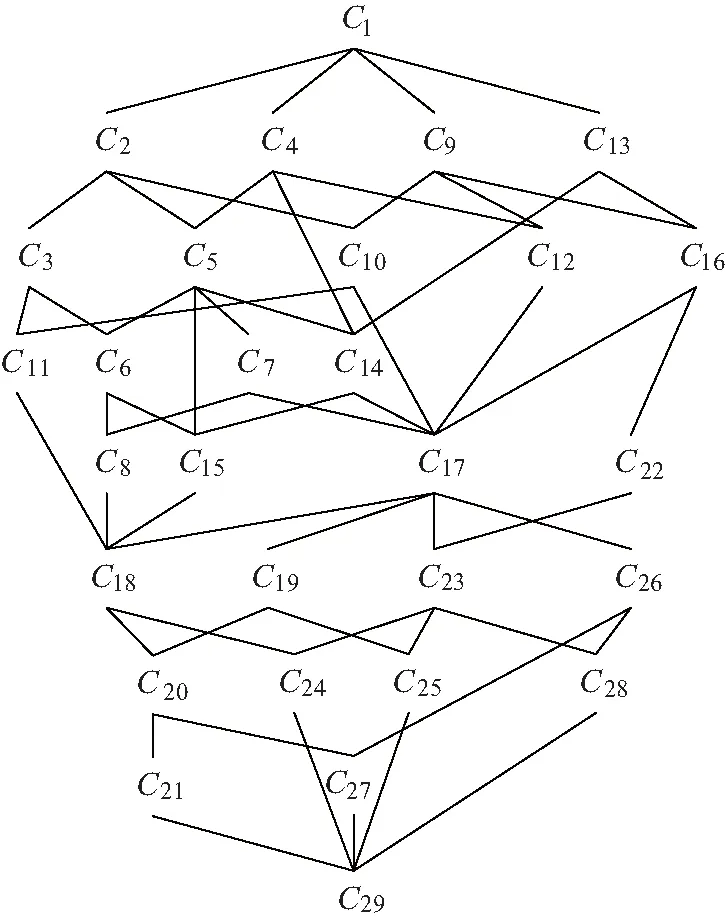
图1 模糊概念格L(K)Fig.1 Fuzzy formal concept lattice L(K)
L(K)中的模糊概念如下:
2 模糊粒的描述
模糊粒描述的基本思想是由模糊原子粒的组合判定一个粒是否可定义,并由模糊原子粒最简描述的组合得到可定义粒的最简描述.
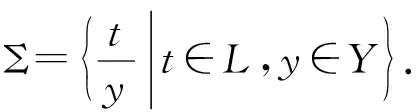
K=(X,Y,I,L)中存在一类基本粒,称之为模糊原子粒,这些模糊原子粒构成了属性概念的外延. 因此,这些粒的最简描述可以直接由属性概念的内涵得到.
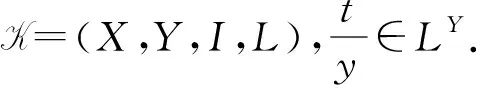
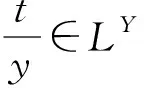
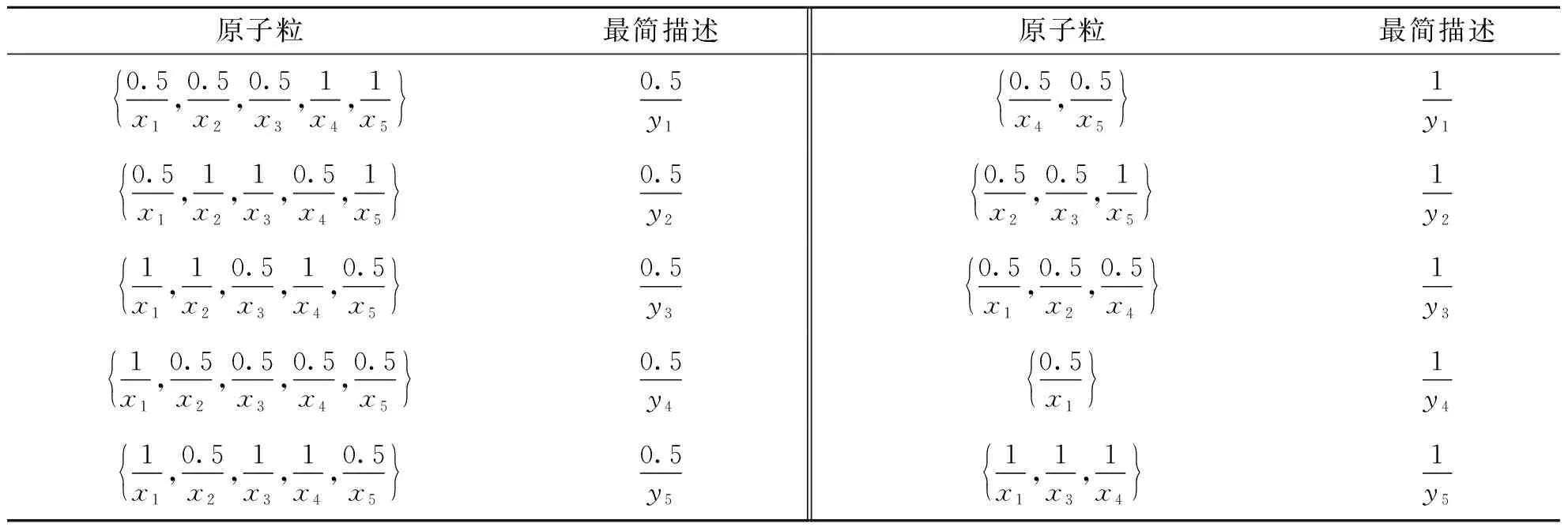
表2 K的原子粒及其最简描述
本质上,任意给定一个粒A,通过遍历Σ的所有子集由定义1便可以确定A是否可定义.进而,若A是可定义的,则可以得到A的最简描述.K的可定义粒及其描述如表3所示.

表3 K的非空可定义粒及其最简描述
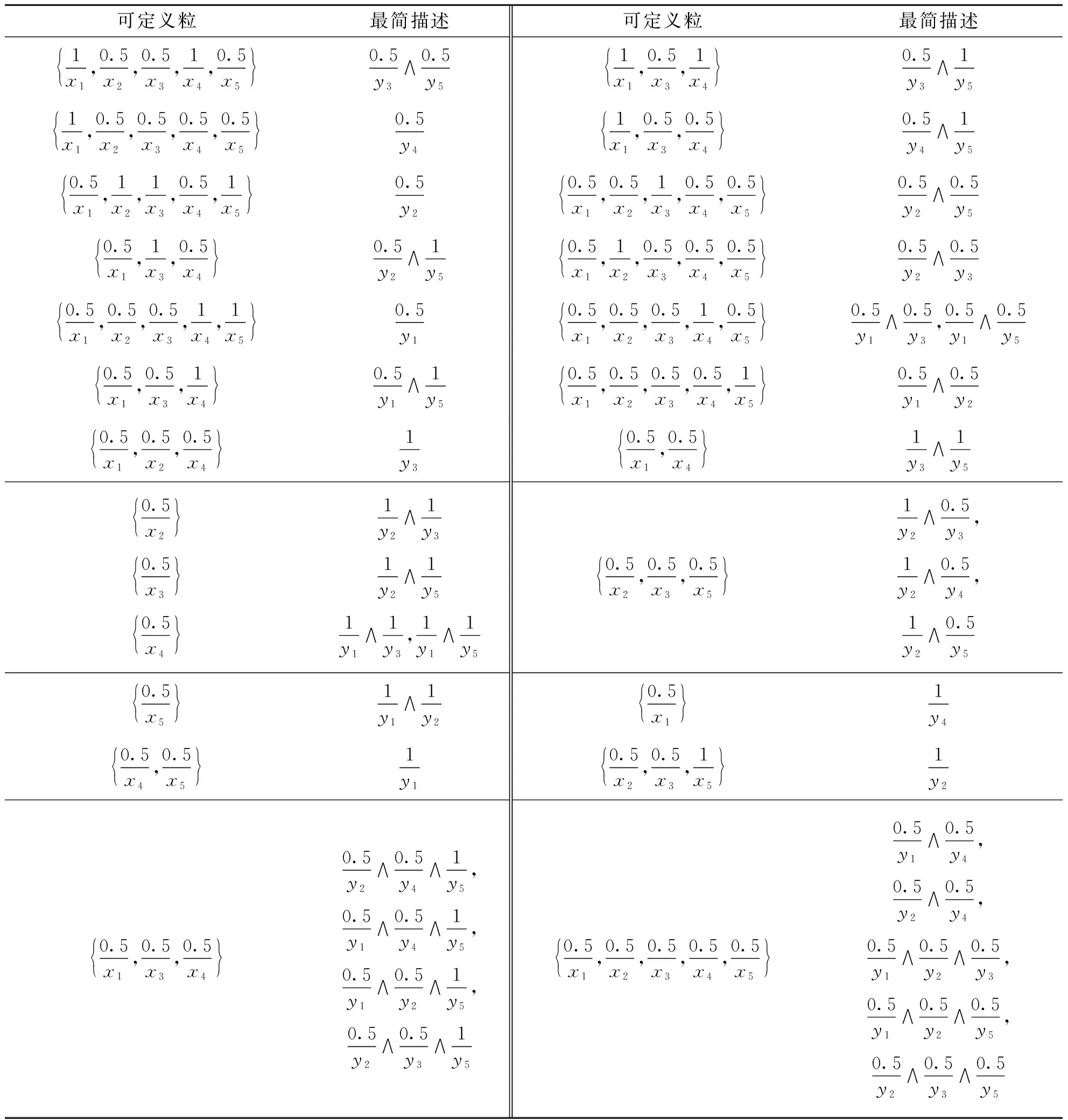
续表3
下面首先定义伪模糊概念,然后讨论如何由伪模糊概念获取完备的模糊概念.
定义3设K=(X,Y,I,L),A∈LX是可定义的.如果C↓=A,那么称(A,C)是一个伪模糊概念.
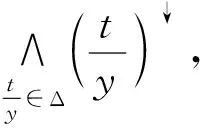
定义4设K=(X,Y,I,L),(A,C)是K的一个伪模糊概念. 定义属性扩充ent(C)=(C∪{y|A⊆y↓}).
由模糊概念的定义容易验证,伪模糊概念(A,C)通过属性扩充,得到的二元组(A,ent(C))便是K的一个完备的模糊概念.
值得注意的是,上述粒描述过程提供了一种构造模糊概念格的有效方法. 首先,找出所有可定义模糊粒,并计算最简描述. 然后,对获得的伪模糊概念进行属性扩充从而获得完备的模糊概念. 最后,基于外延或内涵之间的包含关系对获得的模糊概念进行排序,进而建立模糊概念格.
按照上述过程,由全体可定义模糊粒得到K的模糊概念格如图1所示.
3 基于粒描述的模糊规则获取
形式上,一般规则具有前提和结论,可表示为r:P∧→Q∨.在形式上P∧是属性的合取式,Q∨是属性的析取式.
在下文中,令Pl代表合取式P∧中单个属性的集合,令Ql代表析取式Q∨中单个属性的集合.反之,若C与D是单个属性的集合,则用C∧表示C中属性的合取式,用D∨表示D中属性的析取式.
为了定义模糊形式背景中规则的支持度与置信度,首先引入两个针对模糊集的运算. 在K=(X,Y,I,L)中,A∈LX,用g(A)={A’|A’⊆A}表示包含于A的集合,并用|g(A)|表示g(A)的大小.
定义5设K=(X,Y,I,L),r:P∧→Q∨是K的一条模糊规则. 分别定义r的支持度与置信度如下:
实际上,支持度大于0且置信度为1的模糊规则在应用中也最为普遍,意义也更为明确. 因此,本文只讨论这类规则.
定义6对于给定的模糊概念(A,B),如果P⊆B满足P↓=B↓=A且对于任意的S⊂P有S↓⊂B↓,则称P是(A,B)的一个最小产生子.
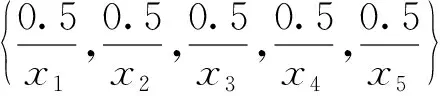
在K=(X,Y,I,L)中,(A,B)是K的一个模糊概念.若(A,B)有一个最小产生子P且B-P≠Ø,则可获取模糊规则r:P∧→(B-P)∨.由最小产生子与置信度的定义可知,r的置信度为1.显然,若A≠Ø,则r的置信度大于0.
定义7设R(K)为K=(X,Y,I,L)的模糊规则的集合. 对于R(K)中任意的两条规则r1:P∧→Q∨与r2:E∧→F∨,若Pl⊇El且Ql⊆Fl,则称r1蕴含r2,记做r1⟹r2.
定义8设R(K)为K=(X,Y,I,L)的模糊规则的集合.对于R(K)中的任意一条规则r,若r不能被其它规则蕴含,则称r是无冗余的.进而,若R(K)中的每一条规则都是无冗余的,则称R(K)是无冗余的,并记做R*(K).
特别强调的是,下文中研究的模糊关联规则均指无冗余的模糊关联规则. 显然,由最小产生子获取的规则是无冗余的. 实际上,对于给定一个可定义粒A∈LX,由它的一个最简描述C∧可以构造一个伪模糊概念(A,Cl),进而通过属性扩充可以得到完备的模糊概念.根据上述讨论可知,此模糊概念蕴含了无冗余规则r:C∧→(ent(Cl)-Cl)∨. 换言之,由一个可定义粒的最简描述可以构造一条无冗余规则的前提,由属性扩充中增加的属性可以构造一条无冗余规则的结论.
对于表1中的模糊形式背景K,它的全部模糊关联规则R*(K)如下:
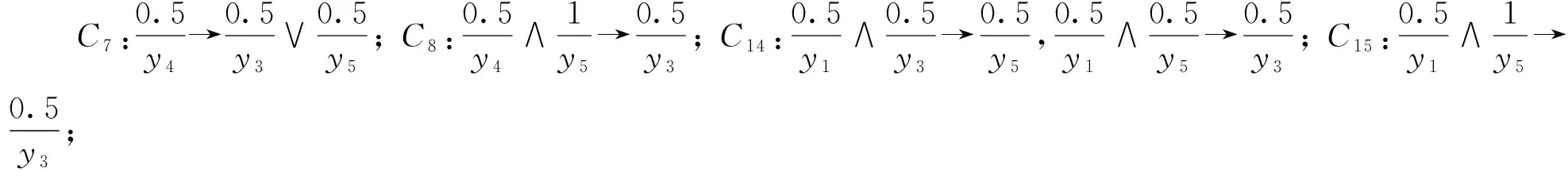
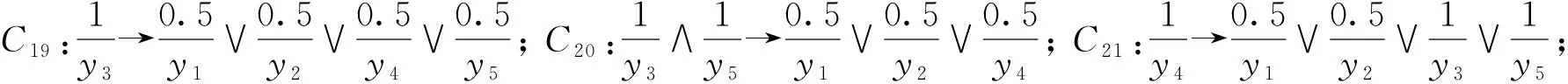
4 实验分析
本小节研究对象数量、属性数量以及填充因子等因素对模糊关联规则规模的影响.
填充因子(Fill Ratio)是度量模糊形式背景数据稠密程度的重要指标,是指模糊形式背景中非零元素所占比例,即
实验采用随机的方式生成不同规模的形式背景. 此外,为了更加客观,每个规模的形式背景重复生成20次,以获取模糊关联规则的数量取平均.
1) 对象数量
在实验中,固定属性数量为15,填充因子为0.5. 记录不同规模形式背景中对象与模糊概念格以及模糊关联规则的数量关系,其结果如图2所示. 在图中,|R|与|L|分别表示模糊关联规则与模糊概念的数量.
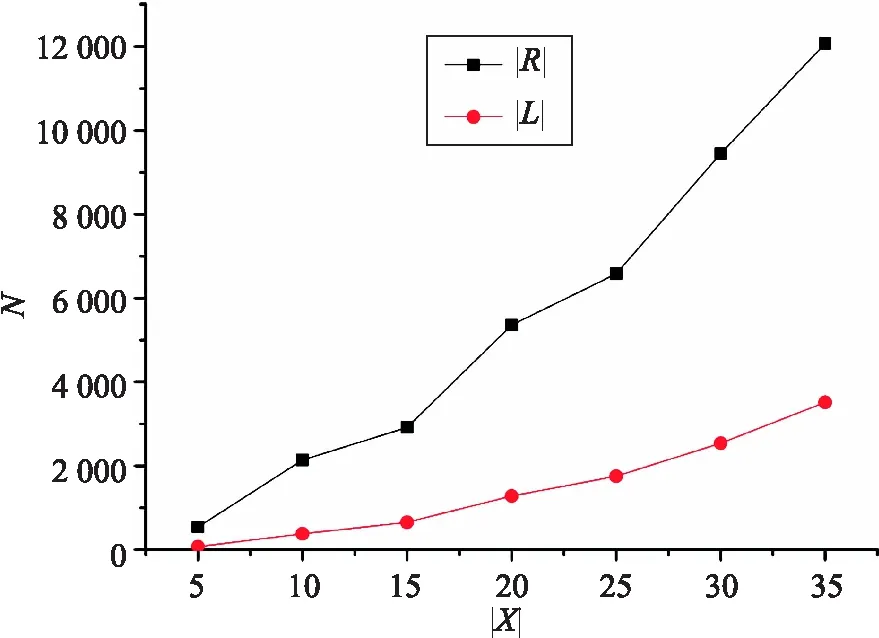
图2 对象数量与模糊概念格以及模糊关联规则规模的关系Fig.2 The relationship between the number of objects and the sizes of fuzzy concept lattice and fuzzy association rules
2) 属性数量
在实验中,固定对象数量为15,填充因子为0.5,记录不同规模形式背景中属性与模糊概念格以及模糊关联规则的数量关系,其结果如图3所示.
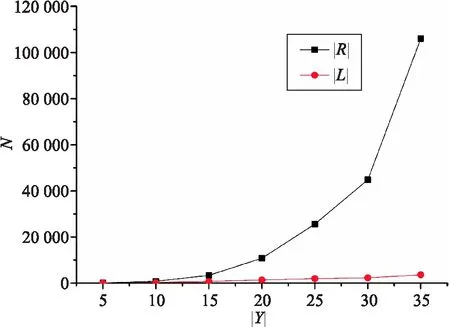
图3 属性数量与模糊概念格以及模糊关联规则规模的关系Fig.3 The relationship between the number of attributes and the sizes of fuzzy concept lattice and fuzzy association rules
3) 填充因子
固定对象与属性数量均为15,记录不同规模形式背景中填充因子与模糊概念格以及模糊关联规则的数量关系,其结果如图4所示.
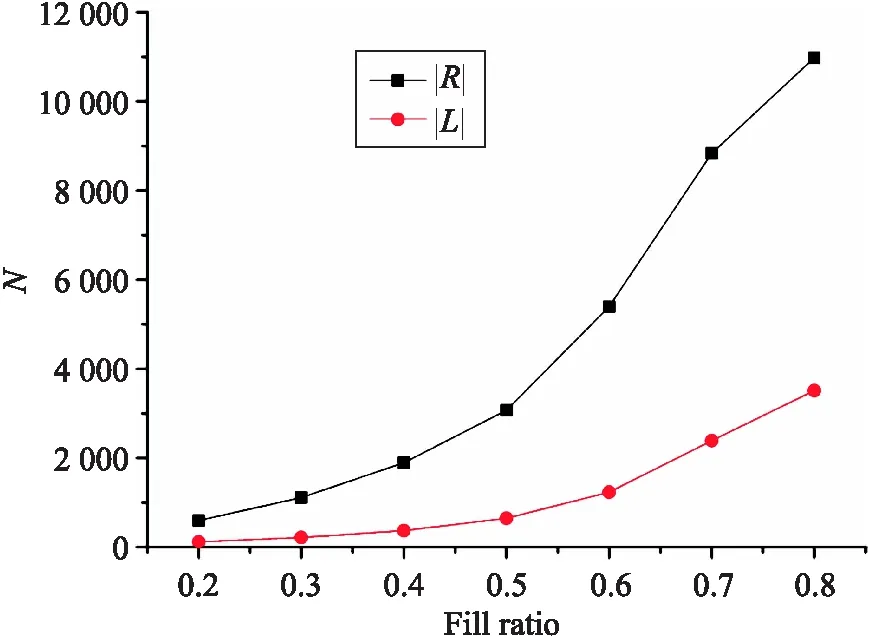
图4 填充因子与模糊概念格以及模糊关联规则规模的关系Fig.4 The relationship between the fill ratios and the sizes of fuzzy concept lattice and fuzzy association rules
实验结果表明增加属性的数量能够大幅度增大模糊关联规则的规模,增加对象数量与填充因子也能够增大模糊关联规则的规模,但幅度远小于增加属性带来的影响.
5 结 论
采用模糊形式背景刻画原始数据,利用形式概念分析这一工具实现可定义粒的描述,进而获取无冗余的模糊规则是本文的主要贡献. 具体结论有以下三点:
1) 从规则与粒的关系出发,用可定义粒的最简描述获取无冗余规则,从而避开了建立概念格与计算最小产生子两个NP难问题.
2) 提出了一种基于属性扩充的模糊概念获取方法.
3) 除了以上的两点,本文的工作与现有的工作也有相似之处. 例如,均采用了外延-内涵角度进行粒描述.
总之,基于粒描述的数据理解是一个很有前途的研究方向,有许多重要问题有待研究. 例如,如何根据粒自身的特点自适应地选择描述逻辑获取粒的最简描述便是一个极为重要的问题.
