基于GS-SVR模型的空腔积水水深和长度预测
2022-11-10郭港归李国栋王立杰
郭港归,李国栋,魏 杰,王立杰
(1.西安理工大学西北旱区生态水利国家重点实验室,陕西 西安 710048;2.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014)
水流掺气[1-2]是防止高水头泄水建筑物空化空蚀的主要措施。然而,小底坡下的掺气坎常出现空腔回水现象,导致空腔形态较差,严重时甚至被积水填满,导致掺气量不足,难以达到掺气减蚀的效果。空腔积水水深和空腔长度是衡量掺气设施效率的重要指标[3],因此研究坎下水力特性与空腔积水水深、空腔长度的关系具有重要的工程价值。前人对空腔积水水深和空腔长度进行了较多的理论公式推导:杨永森等[4]运用动量方程对控制水体进行受力分析,计算出空腔积水深度;徐一民等[5-6]以微元法为基础,建立空腔回水方程计算空腔积水水深和空腔长度,计算值与试验值趋势一致;Chanson[7]利用抛射体公式计算射流空腔长度和回水长度,与实测值相比计算结果偏大;潘水波[8]对抛射体公式引入3个修正系数,计算精度相对提升。
目前机器学习的方法已广泛应用于局部冲刷、水质预测和流量系数预测等水科学领域,人工神经网(artificial neural network,ANN)和支持向量机(support vector machine,SVM)是其中重要的方法。由于ANN需要设置复杂的网络结构参数,导致模型收敛缓慢,甚至在小样本数据下容易造成过拟合[9],降低预测准确度。SVM以最小结构化风险原则代替传统经验风险方法[10],在处理小样本数据中有着天然的优势,泛化能力强,有效防止过拟合,其拓扑结构主要由自身的超参数决定,通过对超参数(C和γ)进行优化使模型达到较高的预测精度。Zaji等[11]用适凑法确定了SVM模型的超参数并对三角形侧堰的流量系数进行预测;Jain[12]通过现场实测数据建立SVM模型模拟河道水位、流量和含沙量的关系;Kiyoumars等[13]采用粒子群算法(PSO)优化SVM模型实现对阶梯溢洪道流量系数和消能率的预测;赵庆志等[14]通过网格搜索的方法对超参数进行寻优,得到了基于LS-SVM的短期降雨预测模型。
本文通过网格搜索和交叉验证的方法建立SVM回归(GS-SVR)模型,研究超参数C和γ之间的规律和其对模型性能的影响。基于GS-SVR模型,依据评估指标判别6种参数输入中的最优组合,实现了对空腔积水深度和空腔长度的准确预测,并采用敏感性分析寻找对该模型起关键作用的因素。
1 试验数据
本文基于沈春颖[15]的试验数据集,建立GS-SVR模型。试验水槽全长7.6 m,槽宽10 cm,来流量的范围为0~5.5 L/s,挑坎体形如图1所示。在不同的挑坎体形和来流条件下进行模型试验,分别测量水深h、挑坎坡度i1、挑坎高度Δ、空腔积水水深h1、空腔长度L、水舌冲击角θ和底坡坡度i2。试验数据总量162组,范围见表1。

表1 试验数据范围
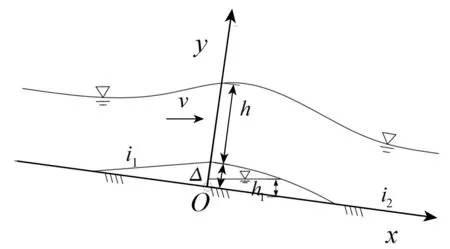
图1 掺气坎布置方式
采用皮尔逊相关系数r反映各变量之间的相关性,皮尔逊相关系数如图2所示,图中v为坎顶流速。试验输出变量包括h1和L,其余除θ以外均为输入变量。当2个变量之间的皮尔逊相关系数|r|>0.3,则认为两变量之间相关性较强,输入变量应避免两两之间有较强的相关性,确保变量的相对独立性。由图2可知,输入变量之间的相关系数的绝对值多数小于0.3,表明各输入变量独立性较好。输出变量h1与Δ、θ和i2的相关性较强,相关系数分别为0.73、0.5、-0.43,当Δ和θ增大时,均导致h1增加,而随着i2增大,h1减少;输出变量L受到Δ和v的影响较大,相关系数分别为0.61和0.57,说明v和Δ增加时,L随之增加。

图2 变量相关性分布
2 GS-SVR模型的建立
先利用量纲分析法确定需要的输入变量,在此基础上选择不同的输入组合,并对其进行归一化处理。采用网格搜索和交叉验证的方法优化不同训练样本比例和输入组合的SVM模型,建立最佳输入组合下的GS-SVR模型,并分析模型超参数C和γ的分布规律。
2.1 量纲分析与变量组合
采用表1中的物理模型试验数据建立SVM模型,预测小底坡低弗劳德数泄洪洞的h1、L。h1和L是衡量掺气设施是否符合要求的重要指标。根据文献[16]可知h1和L均受到以下因素的影响:
Y=f(i1,i2,h,v,Δ,Δp)
(1)
式中:Y为h1或L;Δp为空腔内外压力差。掺气设施通气充分时,Δp对空腔长度和空腔积水水深的影响可以忽略不计。基于量纲分析方法[17],可由式(1)得到:
(2)
由于Δ与h具有相同量纲,因此等效后得到另一种形式:
(3)
变量组合见表2和表3,WD1~WD4与CL1~CL4以式(2)为基础的输入组合,输入变量依次降低,探究变量数目对模型的影响;WD5~WD6与CL5~CL6以式(3)为基础的的输入组合,对比不同量纲化方式对模型性能的影响。

表2 空腔积水水深模型的变量组合

表3 空腔长度模型的变量组合
2.2 数据预处理
2.2.1归一化处理
原始数据中,各变量之间的数值差异较大,影响模型的预测性能,因此对数据进行预处理是必要的。在无量纲化后,采用式(4)进行归一化,统一变量范围到0~1之间。
(4)
式中:xmin为样本数据的最小值;xmax为样本数据的最大值;x*为归一化后的值。
2.2.2训练集、测试集和交叉验证
许多研究者只将数据集分为训练集和测试集,模型从训练集中学习,在测试集中调整SVR模型超参数。而实际中很多时候缺少未来的数据,并且由于测试集用于模型调参,导致测试数据的信息提前泄漏到模型中,造成模型预测结果精度偏高、不能反映模型的泛化性能,容易产生过拟合[18]。为了解决上述问题,需要提取一部分数据作为验证集,模型在训练集上学习,在验证集上调参,测试集用于最终评估。然而,数据集分为3组将大大减少可用于模型学习的样本数量,造成模型训练不充分,导致计算结果存在随机性,而k折交叉验证(k-CV)的方法能有效解决样本容量小的问题。k-CV将原训练集拆分为k个较小的集合,对于每一个小集合都遵循以下原则:①使用k-1折数据作为模型的训练数据;②模型对剩下1折数据进行验证;③k-CV的模型评估指标是k次循环中的平均值(该指标可用于模型泛化水平的度量)。交叉验证的方法不会浪费数据,非常适合数据样本总量较少的情况。本试验将采用五折交叉验证的方法,具体步骤如图3所示。

图3 五折交叉验证示意图
2.2.3训练样本抽取比例
训练样本数量占总样本数量的比重会影响SVR模型的性能。本试验选取训练样本抽取比例分别为50%、60%、70%和80%,采用网格搜索和交叉验证的方法预测空腔积水水深h1和空腔长度L。模型指标选取相关系数R2,不同抽取比例下的分布如图4所示。由图4可知,随着训练样本量增加,训练集、交叉验证集(CV)和测试集的模型指标R2均增加。说明该模型性能随着训练数据的增加而提高。因此,本次试验选择训练集占总样本集的80%为基准比例。
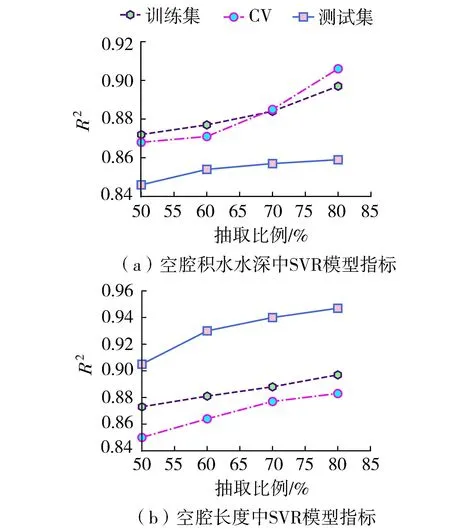
图4 SVR模型指标分布
2.3 网格搜索法优化GS-SVR模型超参数
GS-SVR模型具有良好的泛化性能,而其模型性能依赖于它的超参数[19]。SVR的超参数主要包括正则化系数C和核参数γ。C代表模型复杂度[20-21],C取值较大时,模型会尽可能拟合所有训练数据,可能造成模型过拟合。核参数γ是核函数的内置参数,代表影响支持向量的强度[20]。
网格搜索[22]是最常见的寻优算法之一,其主要目的是让寻优超参数C和γ在一定坐标范围内、根据规定步长划分网格,并遍历所有的网格,对选定的网格节点的所有超参数组合C和γ利用k折交叉验证得到模型交叉验证评估指标(R2),最终取使模型交叉验证评估指标R2最高的那组C、γ为最佳超参数组合。
图5为基于网格搜索下的h1和L预测模型的超参数分布,其中C和γ均在2-8~28之间,分别在各范围内取100个网格点(总网格数100×100=10 000),根据图上的等高线和颜色分布可以找到交叉验证评估指标R2取值较大时的位置。试验结果表明,在所有的输出组合和训练抽取比例下,交叉验证评估指标均呈现相似的分布,因此仅展示3张图(图5)。图5中C和γ对模型性能影响较大。中间黄色区域的R2>0.7,模型性能较好;左上和左下深蓝色区域C取值较小,造成模型欠拟合;图右上浅蓝色区域γ较大导致模型过拟合,模型性能不理想。深黄色区域中模型性能进一步提高(交叉验证评估指标R2>0.86),沿着该区域能够找到交叉验证评估指标R2取值最大的点,该点对应最优超参数组合。深黄色区域中,当C增至+∞时,则γ趋于-∞,说明超参数处于相反的增长趋势。C增大实现模型对样本充分训练,同时减少γ防止其过度训练,最终模型的预测结果处于最佳状态,因此SVR保持其良好泛化性能和高预测精度的机制是通过平衡C和γ的大小来实现的。
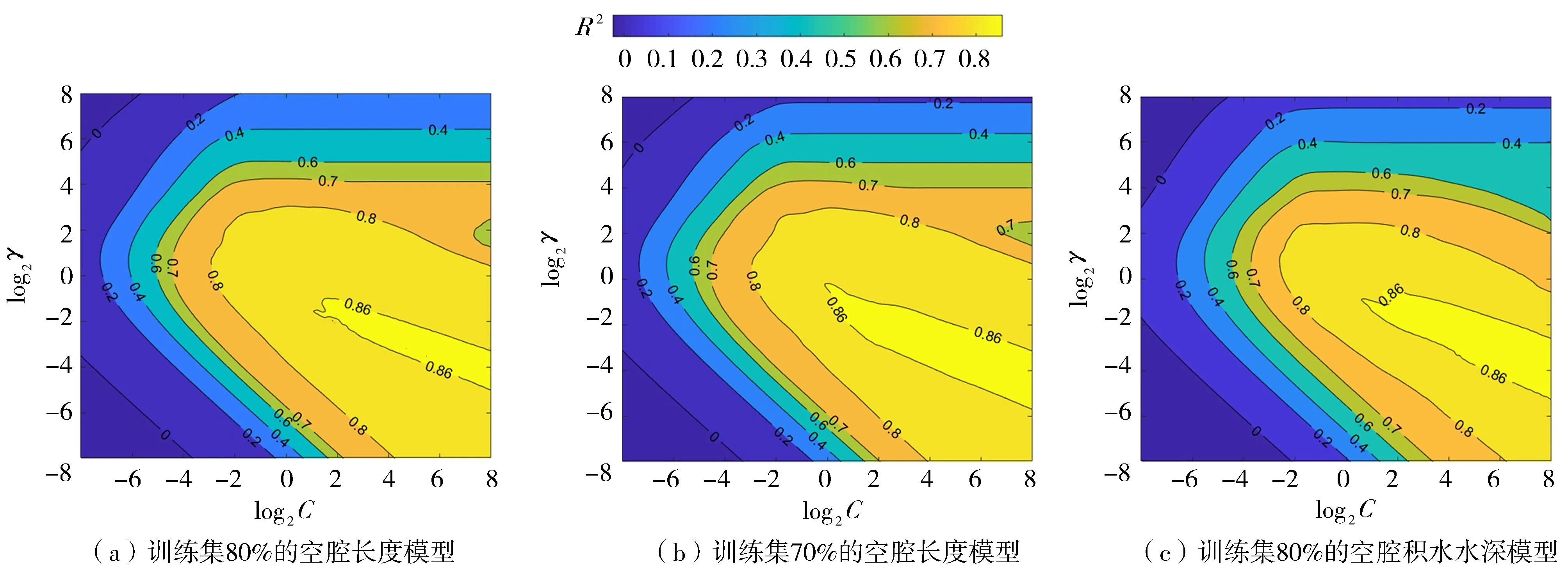
图5 网格搜索中R2的分布情况
3 GS-SVR模型计算结果与分析
3.1 模型计算结果
空腔回水和空腔长度是小底坡、低弗劳德数泄洪洞掺气设施设计中关注的指标,通过GS-SVR分别对6种参数不同输入组合进行分析,模型评估指标选取R2和均方根误差RMSE。
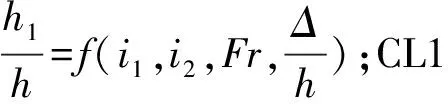
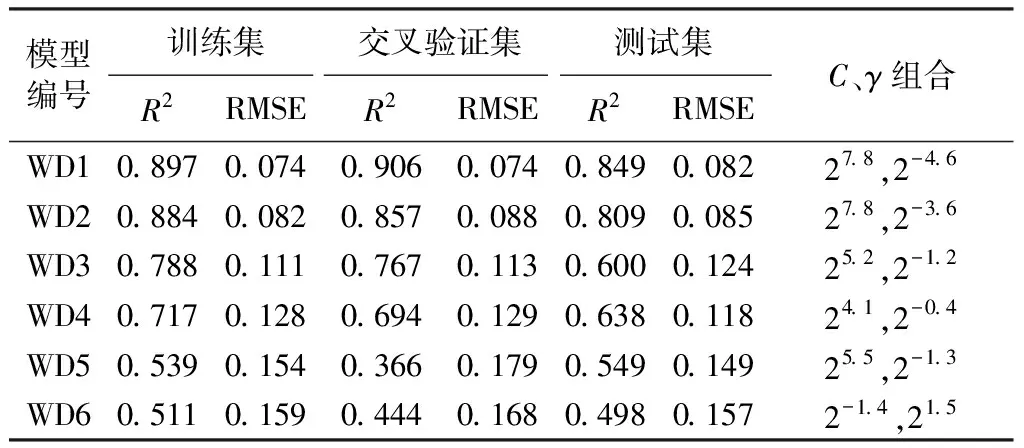
表4 空腔积水水深的模型指标
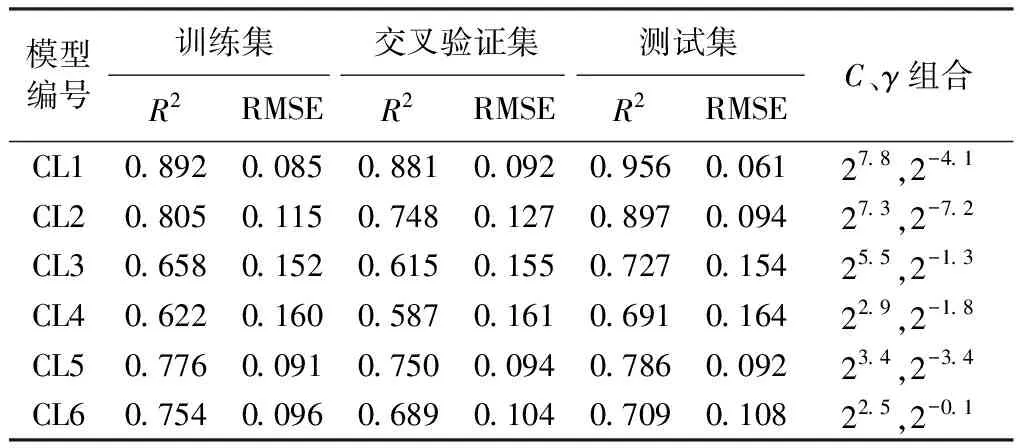
表5 空腔长度的模型指标
3.2 模型敏感性分析
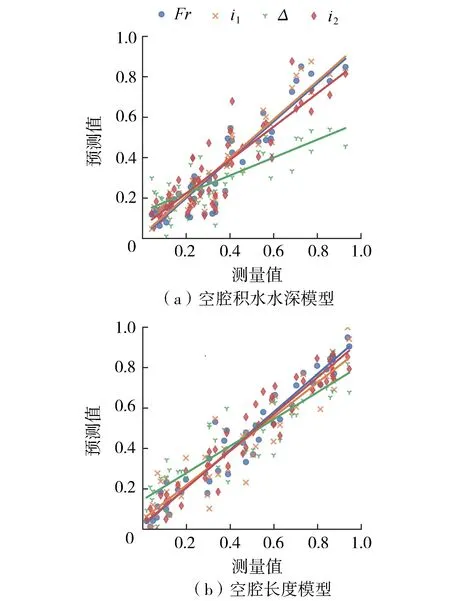
图6 敏感性分析
结合变量相关性分析发现,相关性分析与敏感性分析联系紧密,相关系数大的输入变量对模型影响大。因此,在建模之前可以通过相关性分析选择重要的输入变量。
4 结 论
a.原数据中,各输入变量之间独立性较好;输出变量空腔积水水深和空腔长度均与输入变量存在相关性。根据不同抽取比例训练集的结果发现,小样本容量中,较大的训练集抽取比例能提高GS-SVR模型的性能。
b.通过网格搜索和交叉验证的方法对模型超参数进行优化,发现该方法能找到最佳超参数组合、提高模型性能,并且GS-SVR模型计算结果的高准确度机制是通过超参数C和γ的相互制约来实现。
c.6种不同输入组合的计算结果表明,保持GS-SVR模型复杂度和样本复杂度一致并且采用合适的量纲化方式会极大改善模型性能,在此基础上寻找最佳变量组合,实现对空腔积水水深、空腔长度的精准预测。
d.敏感性分析发现,空腔积水水深模型对坎高和坎下底坡较为敏感,空腔长度模型仅对坎高敏感。本文试验由于弗劳德数变幅较小,而SVM预测结果依赖于试验数据,故建模型的通用性有待考量,未来可收集更多掺气坎体型下的试验数据,扩大模型应用范围。
