基于生物启发神经网络的水下坝面表观裂缝检测路径规划算法

马建业，郑东健,2,3，孙建伟

(1.河海大学水利水电学院, 江苏 南京 210098；2.河海大学水资源高效利用与工程安全国家工程研究中心, 江苏 南京 210098；3.河海大学水文水资源与水利工程科学国家重点实验室, 江苏 南京 210098；4.南京市江宁区赵村水库管理所，江苏 南京 211155)

由于荷载作用、温度变化、体积收缩、不均匀沉降等原因，混凝土坝体、混凝土面板等大体积混凝土结构普遍存在开裂现象。裂缝会破坏结构的整体性，引发渗漏问题，影响结构的整体强度和稳定性，是水工结构运行过程中无法避免的安全隐患，需要进行防治和及时处理。

裂缝检测是裂缝处理的基础性工作，水工混凝土结构裂缝检测方法主要分为人工探视法、破损检测法和无损检测法3类，其中人工探视法虽然局限于裂缝表观特征的检测，但因其具有简便直观、易于操作的优点，仍然是实际过程中使用最为广泛的方法[1]。传统的人工探视法受主观影响很大，检测工作费时费力，在水下等复杂环境条件下，局限性更为突出。自治水下机器人(autonomous underwater robot,AUV)和机器视觉作为新兴的探视手段，已经逐渐成为水下表观裂缝检测的重要手段[2]。由于水下环境复杂，条件有限，目前的研究重点是提高基于图像处理的裂缝识别准确度[3-5]和水下机器人的系统设计[6]。

检测系统和检测结果的可靠性十分重要。但是，由于条件的限制，对于尺寸较大的长裂缝的整体图像不易一次性获取，每次能获取的信息通常是只是被分割的局部信息，不利于后期的图像处理和资料分析。表观裂缝的整体信息对于分析其对结构的影响程度十分重要，对于长裂缝图像的拼接目前已有相关的研究成果[7-8]，在裂缝图像拼接过程中，无论是基于特征检测，还是基于空间拓扑关系的拼接算法，参与计算的图像均是连续获取的相邻两幅图像。故局部图像信息的连续性对于长裂缝图像的拼接尤为重要。如何开展AUV检测工作的路径规划，在连续获取长裂缝局部图像信息的同时保证对检测对象的全覆盖具有一定的研究价值。

路径规划主要包含两种方式：点到点(point-to-point，PTP)规划和全覆盖路径(complete coverage path，CCP)规划。PTP规划的主体思想是避障，其运行路径最短且平滑，目前成熟且应用广泛的算法有A*算法，D*算法等[9]。CCP规划的主体思想是在PTP规划的基础上，力求完全覆盖目标区域。Choset[10]提出可将CCP规划分为环境因素已知的离线式和环境因素未知或部分未知的在线式。根据地图建模方式的区别，CCP规划又可分为单元分解法、线扫分割法、栅格法、四叉树法等，其中栅格法建模方式因其方便、简洁、直观且便于维护，目前应用较为广泛。栅格法建模方式中的牛耕法，或称往复式路径(back and forth path,BFP)法是经典的CCP规划算法，其他经典算法有随机碰撞法、内外螺旋法等。CCP规划算法已经广泛应用于军事、工农业和民用等方面[11]。

Glasius生物启发神经网络(Glasius bio-inspired neural networks,GBNN)作为人工智能的重要内容，被广泛应用于移动机器人路径规划中。Luo等[12]将其与栅格法实时并行实现，并应用到扫地机器人的路径规划中。之后众多学者在机器人的连续转向控制、不确定动态环境的有效避障、降低重复率等方面开展了大量研究[11]。基于GBNN的栅格法路径规划算法得到了不断的完善和发展，成为在不确定动态环境中实时性表现较好的CCP算法。

目前将基于GBNN的栅格法路径规划算法应用到AUV检测表观裂缝方面的研究还比较少，且在水下坝面表观裂缝检测工作中，CCP算法除需要满足基本要求之外，还应尽量保证长裂缝图像获取的连续性，以便获取长度范围跨度较大的长裂缝的整体信息。同时，与传统CCP问题不同，水下坝面可以简化为无障碍物的裂缝信息未知的二维空间。由于工作要求和工作环境的特殊性，需要对水下AUV坝面表观裂缝检测的CCP规划算法进行单独讨论。本文基于GBNN设计了一种用于水下坝面表观裂缝检测的在线式栅格法CCP规划算法，旨在为AUV利用机器视觉检测水下坝面裂缝提供一种路径规划的思路和方法。

1 算法设计

由于水下坝面形状规则简单且部分环境信息(裂缝信息)未知，栅格法是较为合适的建模和规划算法。而基于GBNN的栅格法[13]具有较低的运算复杂程度和较快的路径规划速度，且栅格、坐标及神经元三者存在对应关系，有助于裂缝信息的定位。

1.1 GBNN基本原理

GBNN算法[14]是一种基于神经元活性传递的离散网格模型：将离散的栅格定义为神经元，赋予每个神经元活性值，神经元之间按照一定的连通规则构成神经网络(图1)，活性值在神经网络中按照一定的传递规则进行传递，通过迭代计算获得整个栅格地图中每个栅格的活性值，并应用于之后的路径规划策略。其数学模型如下：

图1 神经元连接结构

(1)

式中：Ai,t为神经元i在时刻t的活性值；wij为神经元i和神经元j之间的连接系数，反映周边神经元向当前神经元i传递活性的权重；f为转换函数，其作用是将活性值转换到(0,1]内，从而保证GBNN算法的收敛性；ci为神经元i的第一状态激励值，将GBNN算法中的状态定义为第一状态，以区别于之后的路径决策中的第二状态。模型其他参数的取值方式可参考文献[15]。

当所有神经元的活性值均在(0,1]内时，表示所有神经元均已被覆盖，路径规划算法停止迭代。需要说明的是，GBNN算法原理中所叙述的神经元与之后水下坝面表观裂缝检测路径规划算法中所叙述的栅格本质上是一样的。

1.2 水下坝面表观裂缝检测路径规划算法

受相机视场范围限制，在水下坝面裂缝检测工作中，无法通过一次拍摄获取长度尺寸较大的裂缝的全貌，需要对长裂缝连续采集多幅局部图像进行拼接。本文设计了一种基于裂缝走向的CCP决策算法，旨在连续地、有组织地获取长裂缝图像，在保证对检测对象全覆盖的同时，完整地、连续地获取长裂缝图像，为之后的图像拼接工作提供保障。图2是算法流程图，其中虚线框内的流程是本算法的关键步骤，也是本文算法设计和研究的重点内容。

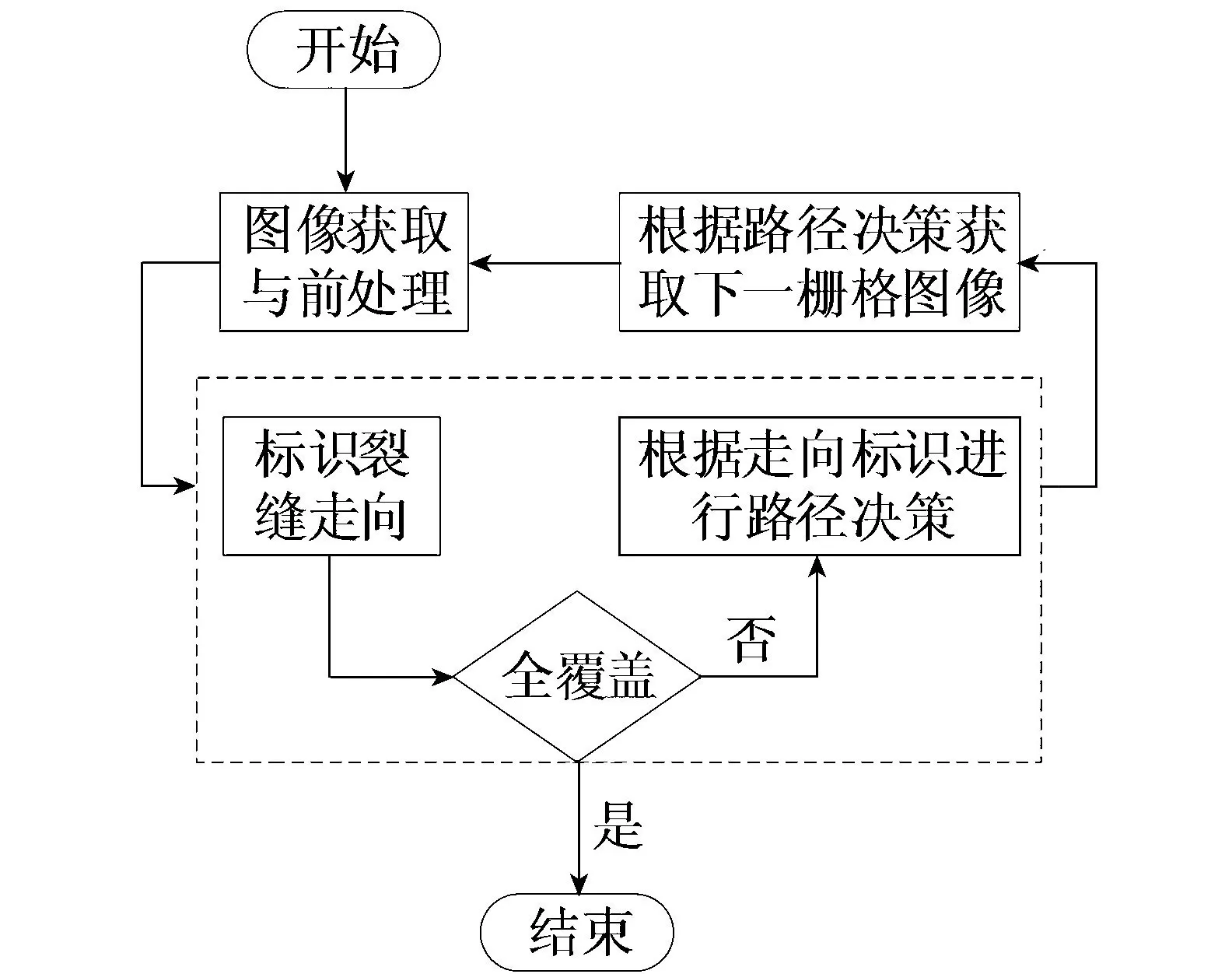
图2 算法流程

图像前处理是路径规划的基础性工作。图像的前处理工作除保证裂缝图像清晰易辨识外，还需包含：图像二值化、图像膨胀、图像腐蚀、细化(骨骼化)、“骨刺”去除和端点识别。图3结合一个算例的处理过程对图像前处理工作的各个步骤进行了具体说明，其中混凝土表面裂缝图片来源于开源数据库[16]。图3仅代表一个栅格范围内的图像信息，并不代表整条裂缝图像。

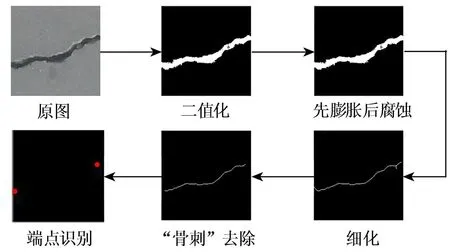
图3 图像的前处理

如图3所示，为区分裂缝和背景，需要对图像进行二值化。先膨胀后腐蚀相当于形态学闭操作，可以对裂缝内部缺失的小对象进行填充，使其成为一个完整的图像。细化又称骨骼化，经过细化处理的图像，高亮部分会逐渐收缩，在保持原来形状的前提下，对高亮部分进行层层剥离，直至迭代到稳定状态后，保留的只是高亮对象的中轴线。每个像素点P有8个邻域，细化处理后保留的像素点应满足每个像素点的8个邻域中，值为1的像素点个数不超过两个。膨胀、腐蚀和细化是基本的图像形态学操作，其原理可参看图像形态学的相关书籍[17]。“骨刺”去除实际上是对对象端点的删除，以达到删除小对象的目的，其删除的像素点满足以下条件：像素点本身值为1，且像素点的8个邻域中有且只有一个1。端点识别是“骨刺”去除的反操作，其保留的像素点是“骨刺”去除步骤中删除的点。需要说明的是，“骨刺”去除删除的不仅是小对象，同时也会对图像主体对象(裂缝)产生影响，使得图像主体对象端点不断内移，长度逐渐缩短。故应根据实际目标图像，对“骨刺”去除步骤的迭代步数进行合理控制。

对图像的前处理工作完成后，得到只包含对象端点的图像矩阵，需要用维数与之相同的标识矩阵与图像矩阵对应的元素进行逐一相乘操作，对裂缝对象的走向进行标识，用于确定下一次扫描栅格的位置。标识矩阵除维数需要和图像矩阵保持一致外，其内部数据结构也需要满足一定的要求。如图4所示，其内部数据大致分为3个大区：核心区、边线区和角线区。其结构类似于8连通链码[18]，但具体取值上与之有所不同，其中核心区相当于链码的中心像素点，值为0，核心区的存在只是为了使矩阵维度与图像矩阵一致，不具备标识意义。边线区和角线区各自包含4个分区共同组成8连通链码的8个不同角度的连通方向，其作用是对裂缝走向进行标识，边线区的4个分区数值分别取10、20、30和40，角线区的4个分区数值分别取11、21、31和41。需要说明的是，边线区和角线区的具体取值并不需要做严格限制，只要这些数值可以代表并计算出8个不同角度的连通方向即可。

图4 标识矩阵结构

如式(2)所示，理想情况下，边线区和角线区的范围只需占据标识矩阵M的最外围一层，但如前所述，在前处理工作中，涉及滤波去除噪点等小对象的操作，会导致本应在图像矩阵边缘的端点向内部移动，如果用类似于式(2)的标识矩阵处理，对标识起到具体作用的边线区和角线区会错过端点，导致标识失败。

(2)

为保证标识矩阵能够“击中”端点，需要适度扩大边线区和角线区，如式(3)所示。但也不能过大，过大可能导致在前处理工作中未被有效处理的噪点等小对象的端点加入计算，扰乱标识结果。标识矩阵各区域的大小需要根据目标本身和前处理结果具体选定：边线区和角线区的最小“尺寸”应由图3端点识别结果中处于“内层”的端点所处的位置决定。

(3)

根据标识矩阵M对处理后的图像矩阵进行处理，如式(4)所示，具体的方式是将标识矩阵M和经过前处理的图像矩阵I的对应元素相乘，得到新的走向矩阵Z。

Z=MI

(4)

理想情况下，由于经过前处理的图像矩阵中只含有裂缝对象端点，故Z中只有两个值非零。但也不排除一个栅格中不含裂缝或含有多条裂缝，这时Z中元素就可能全为0或有多于两个的非零二位数。无论哪种情况，矩阵Z一定是一个稀疏矩阵。如式(5)所示，利用矩阵Z中的非零值计算裂缝走向的等效角度γ，每个非零值均对应一个角度。

(5)

式中：z为矩阵Z中的非零元素；⎣z」表示对元素z向下取整。

假设正在处理的栅格在整个地图中的位置是(m,n)，则根据γ可以求出其指向的栅格位置索引γ′，如表1所示。

表1 裂缝走向等效角度与栅格位置索引

根据标识结果栅格位置索引γ′，赋予被标识的栅格活性增益值gij为1，其余位置的栅格活性增益值gij为0。

如式(6)所示，根据目标邻域各个栅格的GBNN算法计算的活性值Aij，第二状态值sij和活性增益值gij计算目标邻域各栅格的最终活性值pij，并从中选取活性最大的作为下一个目标栅格。

pij=Aij+sijgij

(6)

各栅格的第二状态值的初始值为1，并按照以下规则进行更新：

(7)

(8)

单独设置第二状态变量和利用上述更新规则更新第二状态是出于以下原因而考虑的：如图5所示，包含裂缝的目标栅格图像若不是位于裂缝首尾或整体栅格地图边缘处，经上述方法处理后，理论上至少存在两个指向栅格，若一个目标栅格中存在多条裂缝或交叉裂缝，则会有更多的指向。只能选择其中一个作为下一个目标栅格，但两个指向方向上的图像均属于同一裂缝。第二状态只有在此栅格所指示的栅格都被覆盖之后才为0，否则为1。此时，有多个指向的栅格相当于一个连接点，将被重复扫描，重复扫描的次数不少于其不同的指向个数。此步操作可以将各个指向方向上的裂缝图像连接，避免长裂缝被分割，有助于保证长裂缝的完整度。同时，由于第二状态与GBNN算法中的第一状态是分别赋值和更新的，故可以避免影响GBNN算法的收敛性。

图5 含有多个指向的栅格

综上所述，本文设计的水下表观裂缝检测路径(apparent fracture detection path,AFDP)算法的基本表达式为

(9)

2 仿真试验与分析

为验证AFDP算法的可行性，进行了仿真试验。在试验图像对象选取方面，由于研究重点不是图像处理以及对裂缝的识别，而是路径规划，故从开源数据库[19]选取某水电站溢洪闸门门槽的两幅较为清晰的水上裂缝图像和一幅较为模糊的水下裂缝图片进行仿真试验。

将选取的混凝土表面裂缝图像作为处理目标(图6)，模拟长裂缝的整体图像，将其进行栅格化处理，每个栅格代表摄像机一次能获取的图像范围。整体图像和栅格为标准的正方形，边长为300像素，每个栅格的边长为50像素。

图6 长裂缝图像的栅格网络

选取算法对长裂缝的扫描路径与长裂缝整体图像在栅格中的位置之间的连续度FB为评价指标。FB越接近100%表示连续度越高。FB表达式如下：

(10)

式中：B为长裂缝扫描路径断点个数；T为长裂缝所占总栅格数。

图7是对扫描路径中断点的定义和解释，其中，上方虚线框中的绿色扫描路径中包含一个断点。但与之相似的下方虚线框中的绿色扫描路径是有连接点的情况，不属于断点。

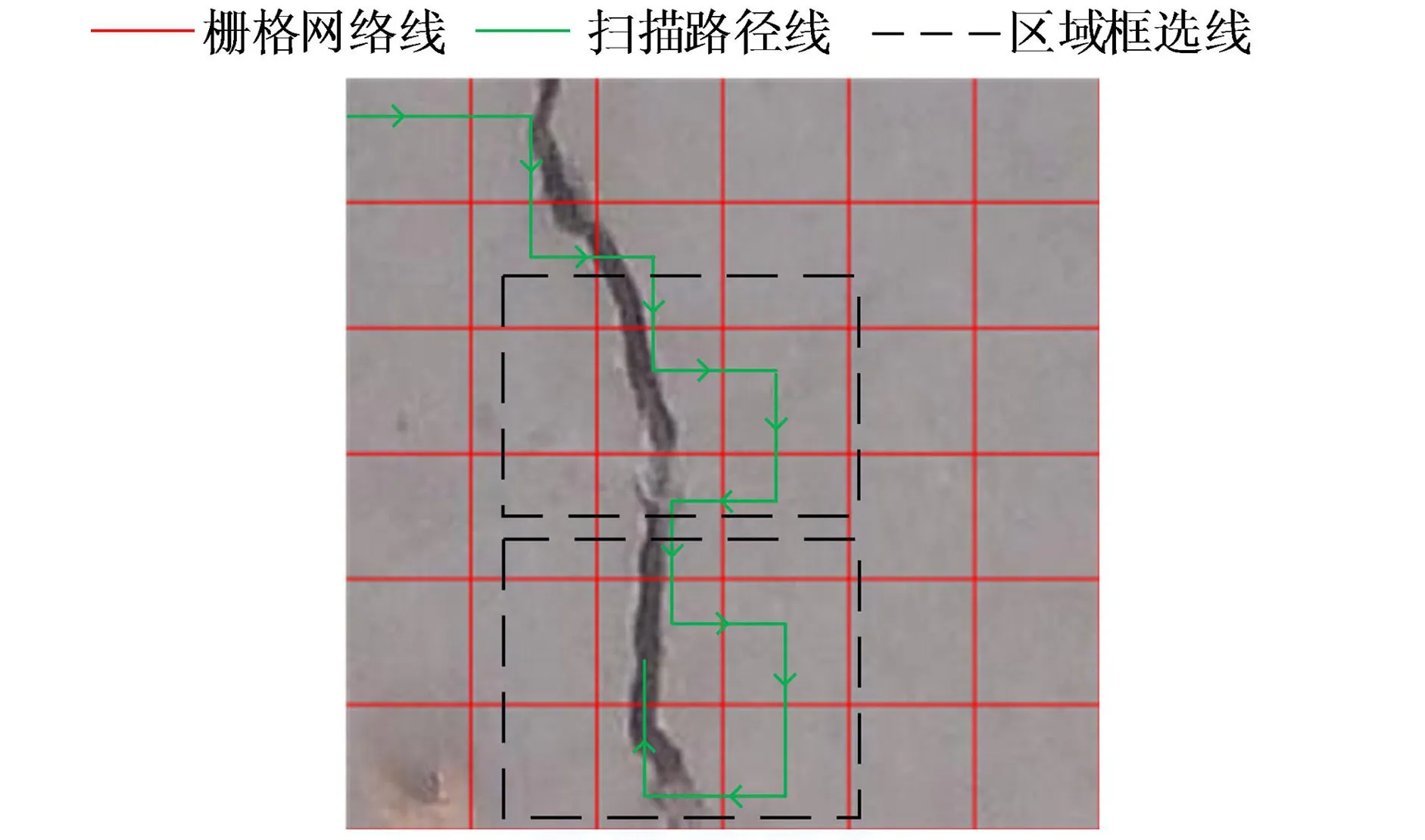
图7 对路径中断点的定义和解释

除连续度外，还需关注覆盖率FH和重复率FR两个指标：

(11)

(12)

式中：H为已覆盖的栅格数；R为重复覆盖的栅格数；T′为总栅格数。

在对比试验算法选取方面，由于BFP算法[11]是CCP问题中最为经典且应用广泛的路径规划方式，且基于GBNN的栅格法路径规划方式若不考虑裂缝走向将退化为BFP算法，故选取BFP算法与本文设计的AFDP算法对3幅长裂缝图像进行处理后进行结果对比。

分别对图像进行栅格化处理后，对得到的栅格网络进行路径规划。其中算例1是较为简单的单条裂缝，不涉及有连接点的情况，算例2是较为复杂的交叉裂缝，会涉及有连接点的情况。算例3是较为模糊的水下裂缝图像。试验结果如图8～13和表2所示。

图8 AFDP算法对算例1的处理结果

图9 BFP算法对算例1的处理结果

图10 AFDP算法对算例2的处理结果

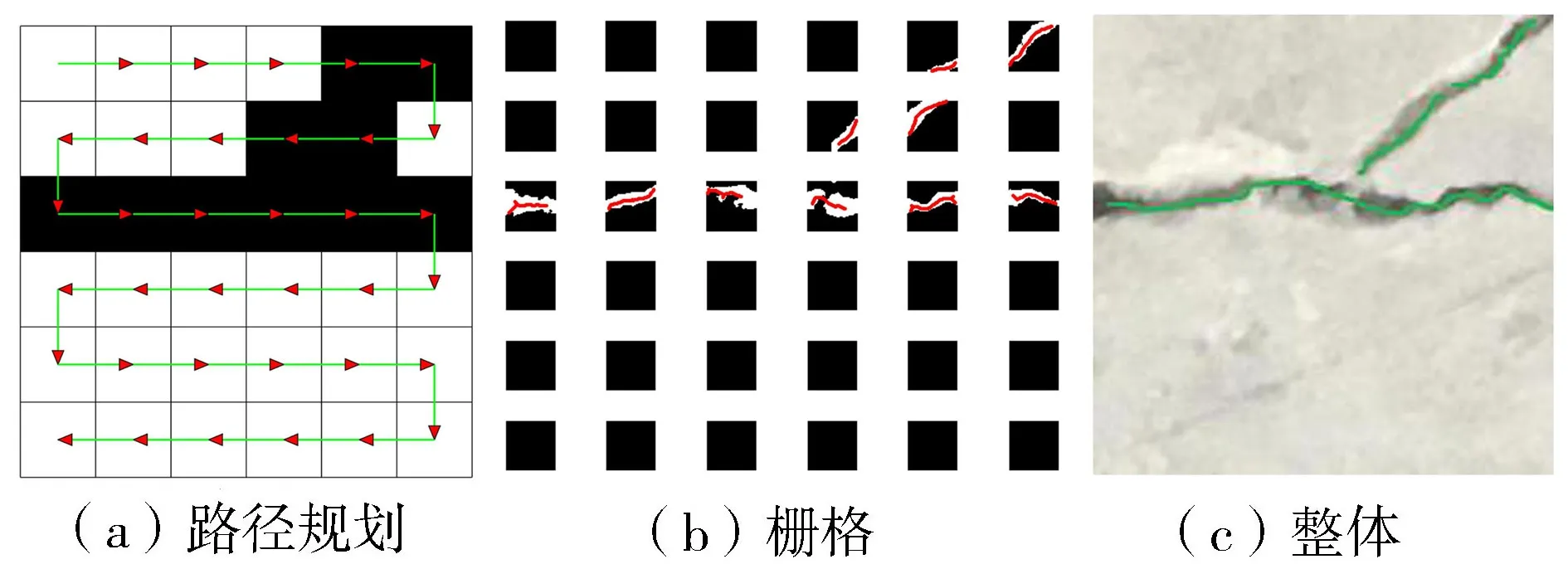
图11 BFP算法对算例2的处理结果

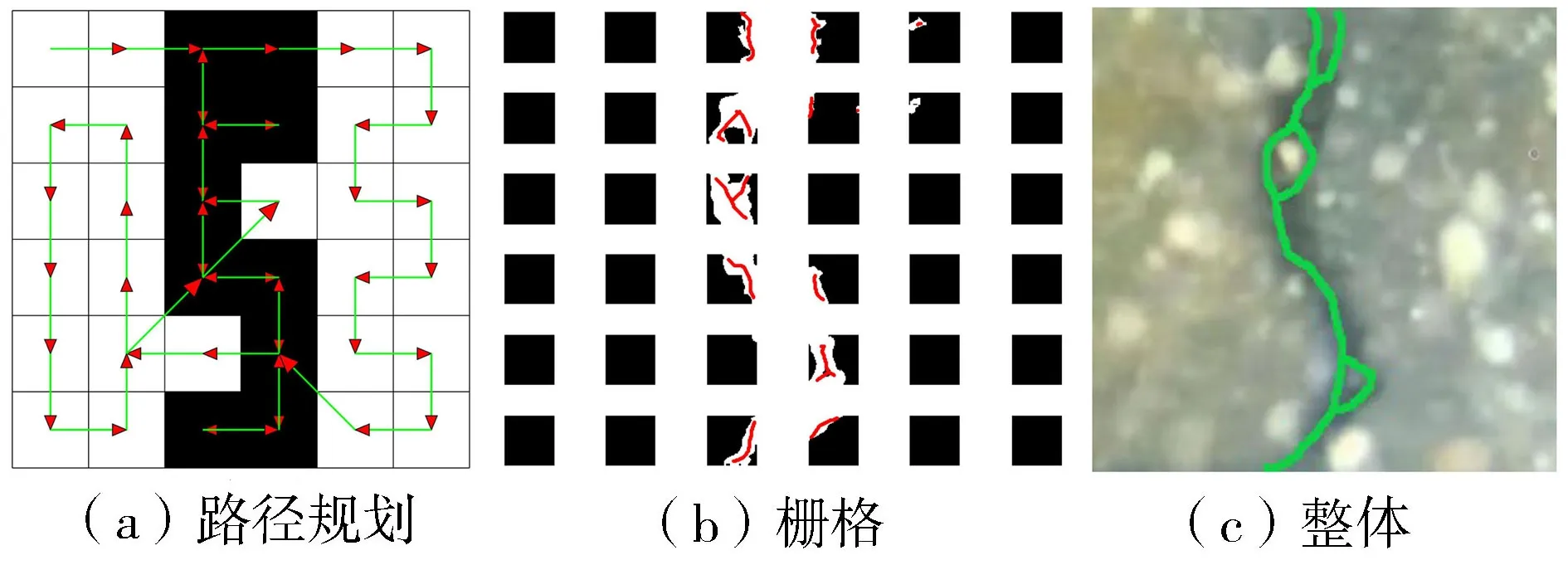
图12 AFDP算法对算例3的处理结果

图13 BFP算法对算例3的处理结果

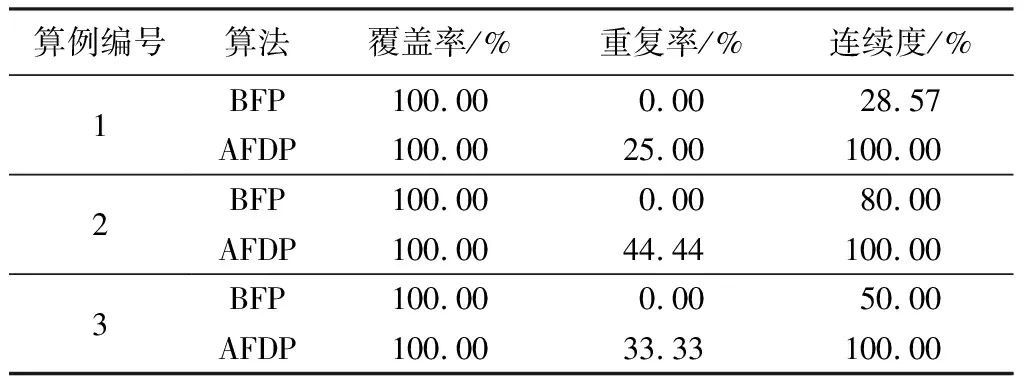
表2 仿真试验结果

据仿真试验结果所示，AFDP算法虽“牺牲”了一定的重复率，但能在保证对检测对象完全覆盖的前提下，对长裂缝图像进行完全连续的扫描，连续度较BFP算法所规划的路径有较大的提升。

3 结 语

本文基于GBNN基本原理设计了一种自治水下机器人的AFDP算法。算法对裂缝走向进行标识，并计算出其指向的栅格，并将指向结果通过活性增益的方式应用到路径决策中。仿真试验结果证实了AFDP算法能够在保证对检测对象全覆盖的前提下，提高对长裂缝扫描的连续度。AFDP算法有望应用于自治水下机器人水下坝面表观裂缝检测工作中，提高长裂缝局部图像信息获取的连续性，对后期长裂缝局部图像的拼接工作提供帮助和支持，以掌握长裂缝的整体信息。