中高速磁浮直线发电机感应电动势影响分析

杨 晨，何云风，张 蕾

(中车株洲电机有限公司，湖南 株洲 412001)

0 引 言

随着高铁发展对于车辆运行速度提高的不断追求，应用磁悬浮技术的车辆相对依靠轮轨黏着力的传统车辆具有较好的高速运行优势，有能耗低、噪声小、振动小、起动制动快、爬坡能力强、维护量少等优点，应用前景非常广阔[1-3]。

为了满足高速运行时磁浮列车的大功率电能传输，中高速磁浮列车均采用长定子直线同步电机结构，其电机定子沿轨道安装于地面，并由地面供电系统直接进行供电，而车载设备则可由内置悬浮电磁铁中的直线发电机在车辆达到一定运行速度以上时感应发电来供电，该种结构可以实现车辆的非接触供电，取消类似受电弓和车载逆变器等设备，减重同时能够保证磁浮列车高速供电的可靠性和安全性[4-5]。

针对直线发电机的感应发电，国内外研究较少。文献[6]采用电磁场有限元法并引入了“滑动表面”模型计算了感应电动势的大小及波形。文献[7]详细分析了定子绕组产生的一阶、二阶齿谐波发电的原理，继而分析了两种不同直线发电机绕组连接方式的感应电动势差异。文献[8]通过解析法导出了感应电动势的计算公式，并利用有限元分析了电机主要参数的变化对感应电动势的影响。文献[9]基于发电线圈的数学模型和数值计算编制自动计算程序以优化结构设计。文献[10]通过高速常导磁浮列车直线电机模拟实验台和二维电磁场，分析了直线发电机的各条发电特性的波形、大小、频率及时间相位差。文献[11]则对直线发电系统的升压斩波器的功能、性能指标进行了分析研究。

总的来说，缺少对悬浮电磁铁上各个直线发电机之间感应电动势的分析。

本文将针对直线发电机的非接触感应发电，简单介绍了直线发电机的基本工作原理，理论推导了感应电势的表达式，利用有限元仿真分析定子磁场、车辆运行速度、气隙、车辆载荷等对其各个直线发电机的感应电动势影响。

1 直线发电机的工作原理

中高速磁浮列车用长定子直线同步电机二维横截面结构如图1所示。直线电机定子沿轨道全线铺设，倒置固定于轨道下方，定子绕组为波绕组；直线电机动子，即悬浮电磁铁，安装于车辆底部，成抱轨结构。

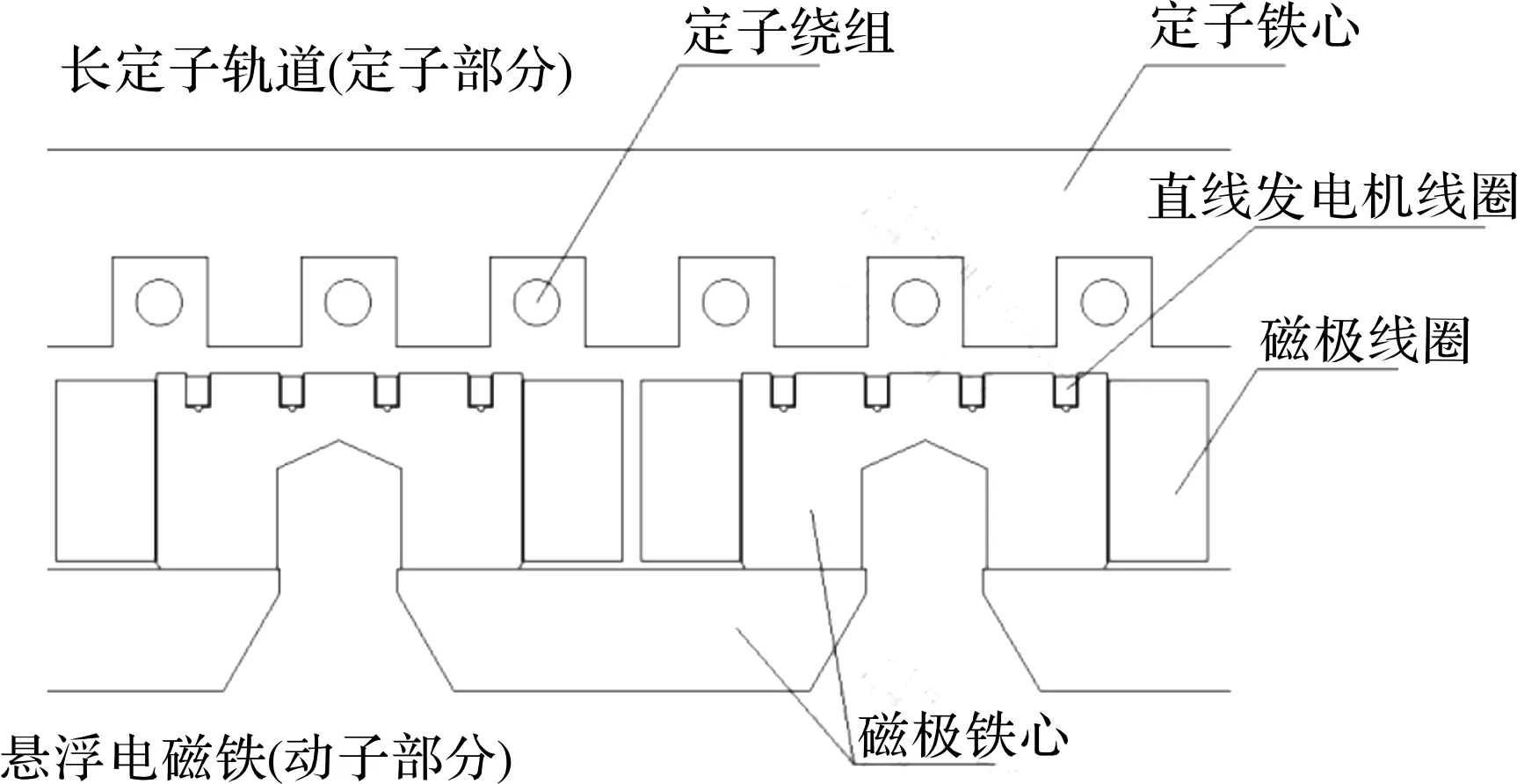
图1 中高速磁浮列车长定子直线同步电机结构图

标准悬浮电磁铁一般包含12个磁极，沿直线排列，通直流电励磁后呈N、S极性交替排布。除两端的2个端磁极外，另外10个磁极铁心均内嵌有2个的发电线圈，串联组成1个直线发电机，即单个悬浮电磁铁有10个独立的直线发电机，如图2所示。

图2 悬浮电磁铁的三维对半结构

定子磁场和悬浮电磁铁磁场均通过悬浮电磁铁铁心、气隙、定子铁心形成闭合磁路。当磁浮列车运行时，由于定子齿槽效应的影响导致气隙大小呈现周期性变化，此时气隙磁场除了与定子电流频率相同的基波外，还有定子齿槽引起的6倍基波频率的谐波及其它高次谐波，而直线发电机的感应电势主要由6次谐波引起[12]。

2 理论分析

长定子直线电机为直线同步电机，但为了削弱齿槽效应对电磁力的影响，其定子极距和悬浮电磁铁极距设计为不相等的电机结构。

气隙磁密主要由磁极磁场和定子磁场决定，但由于每个磁极与定子相对位置不同，则导致每个磁极处气隙磁密受定子磁场影响均不一样。

在车辆运行时，每个磁极内嵌的直线发电机由于定子齿槽导致气隙周期性变化，穿过闭合发电线圈的磁通也随着周期性变化，位置与定子齿对着时磁通最大，与定子槽对着时磁通最小。

2.1 电磁铁中间位置

以悬浮电磁体的中间两个磁极为例进行分析。悬浮电磁铁与定子的相对位置的特殊两种状态，即图3所示的磁极铁心发电线圈环绕的齿与定子齿对应的状态，图4所示的与定子槽对应的状态。

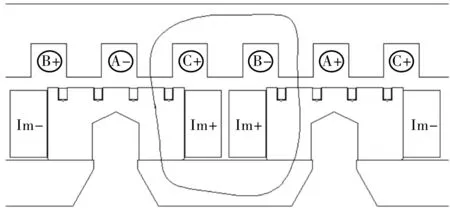
图3 电磁铁中间位置处两个磁极初始位置

假设条件：(1)忽略磁极的漏磁；(2)忽略轨道定子铁心和磁极铁心的磁阻。定子的三相交流电流为

IA=imsin(ωt+ω)
IB=imsin(ωt+φ-120°)
IC=imsin(ωt+φ+120°)

(1)

式中，im为交流电流的最大值，ω为电源角速度，t为时间，ψ为电源初始相位。

根据图3的闭合磁路，有公式：

2H0δ1=2NI+IC0-IB0
Φ0=nμ0H0S

(2)

式中，H0为t0时刻气隙磁场强度，δ1为气隙大小，μ0为空气的相对磁导率，S为气隙的有效截面积，Φ0为t0时刻磁通，IBo为t0时刻IB的电流值，ICo为t0时刻IC的电流值，n为发电线圈匝数，N为磁极线圈匝数。

图4 移动一个齿宽距离后两个磁极位置

根据图4的闭合磁路，有公式：

2H1(δ1+h)=2NI+IA1+IC1-IB1
Φ1=nμ0H1S

(3)

式中：H1为t1时刻气隙磁场强度，h为定子铁心槽深，Φ1为t1时刻磁通，IA1为t1时刻IA的电流值，IB1为t1时刻IB的电流值，IC1为t1时刻IC的电流值。

根据式(2)和式(3)，该单个发电线圈的感应电势为

(4)

当式(4)中ωt0=0，ωt0=30°，ψ=90°，则：

(5)

由式(5)可得，在中间处磁极的直线发电机感应电动势与定子磁场无关。

2.2 电磁铁端部位置

端部两个磁极在t0时，初始位置如图5所示。

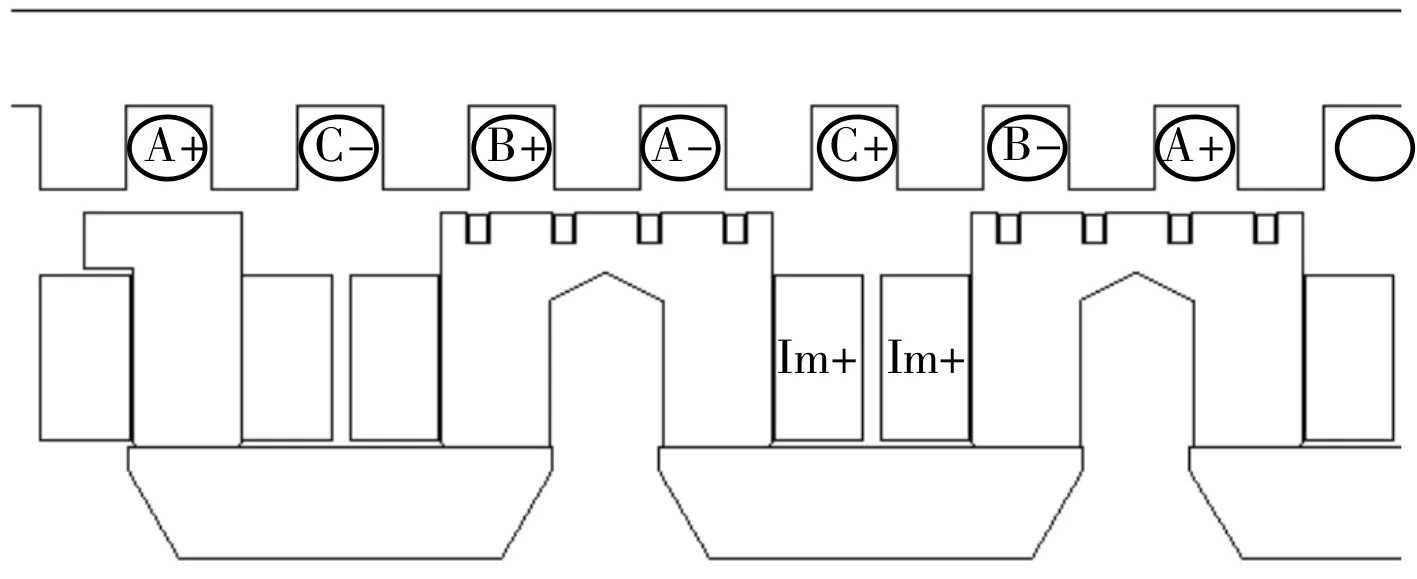
图5 电磁铁端部位置处两个磁极初始位置

当悬浮电磁铁运动34 mm距离后，即t2时刻达到发电线圈最大磁通位置，如图6所示；再运动一个齿距43 mm后，即t3时刻达到发电线圈最小磁通位置，如图7所示。

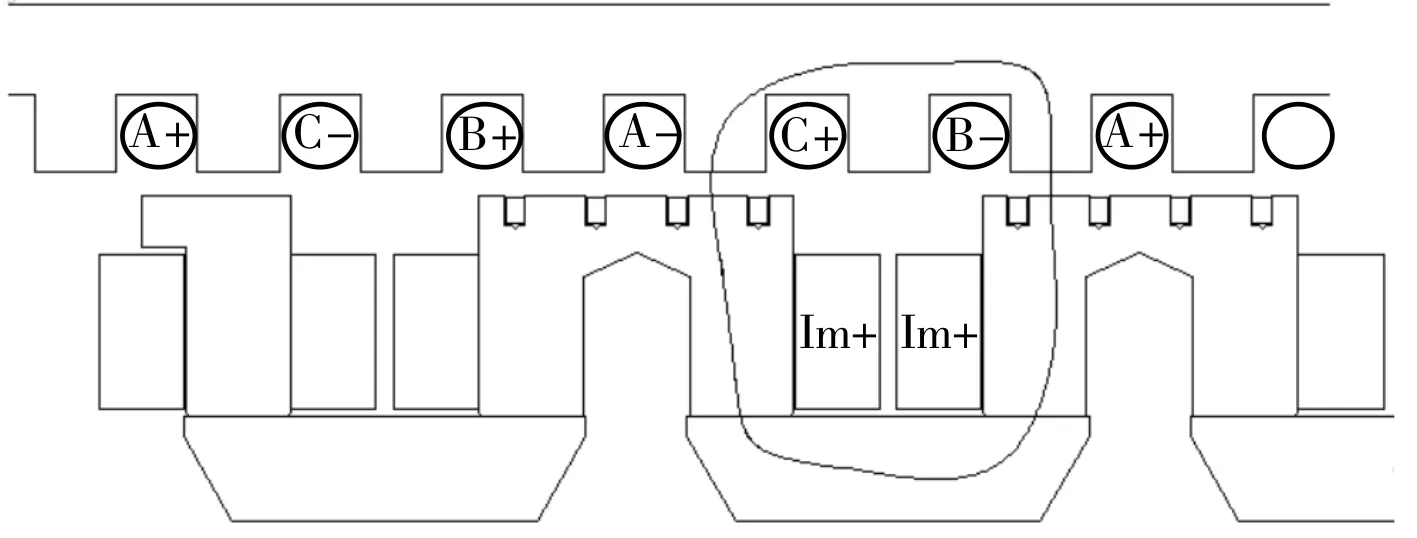
图6 磁通最大时磁极与定子相对位置

图7 磁通最小时磁极与定子相对位置

参考式(4)，该单个发电线圈感应电势为

(6)

式中,ωt2=0，ωt3=30°，ψ=90°。假设I=30 A，im=1.414*1800 A，其它参数根据直线电机结构，则：

(7)

由式(7)可得，在端部磁极的发电线圈感应电势与定子磁场相关，不能够忽略其影响，其对端部磁极的直线发电机的感应电势起到增加或者减小的作用。

3 有限元仿真分析

因长定子直线电机复杂结构结构，其定子与动子均有齿槽，气隙磁场分布比较复杂，通过有限元仿真软件Ansys能比较直观的得到各个直线发电机的感应电势波形及电动势大小。

因此，利用Ansys建立二维动态电磁场仿真模型，分析定子磁场、定子电流、气隙、载荷等因素对直线发电机感应电势的影响。

3.1 定子磁场对感应电动势的影响

3.1.1 定子电流为1800 A时

当定子电流为1800 A，频率为100 Hz时，从悬浮电磁铁的左侧到右侧，10个直线发电机的感应电势波形如图8和图9所示。

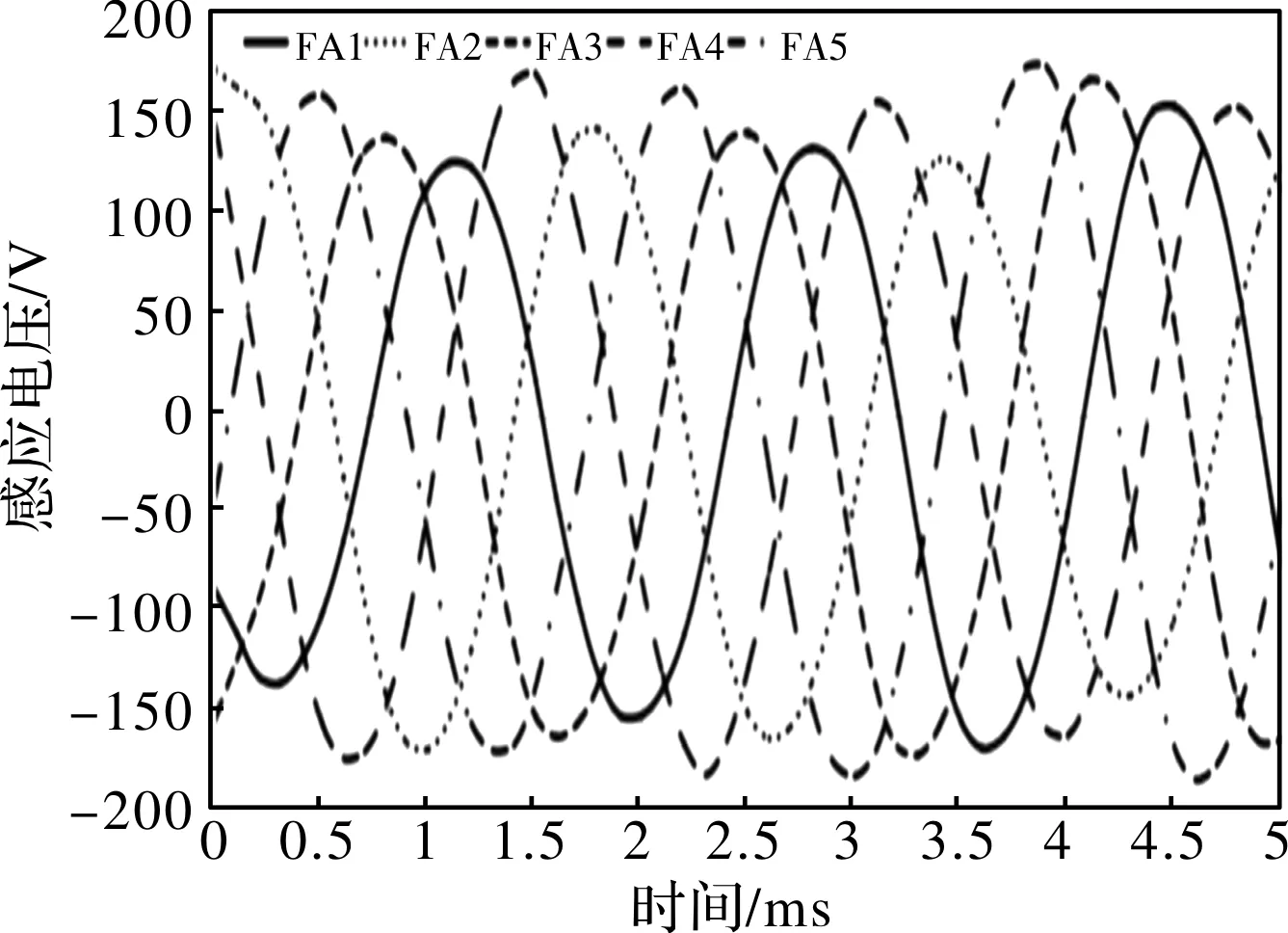
图8 左侧5个直线发电机的感应电势波形图(定子电流1800 A)

图9 右侧5个直线发电机的感应电势波形图(定子电流1800 A)

由图8 和图9可得，左侧5个直线发电机感应电动势小于右侧5个直线发电机，应该是定子磁场对于左侧磁极所产生气隙磁场起到弱磁作用，而右侧起到增磁作用的原因。这是因为定子极距与动子极距不相同，导致每个磁极磁场与定子磁场相对位置关系不一样。

对左侧第一个直线发电机FA1的波形做FFT分析(选取了4个周期)， 得到图10所示的频谱图，其感应电势由一系列谐波组成，其基波频率为600 Hz，基波电压的峰值为154.5 V，则该FA1线圈感应电压的峰值为155.7 V。

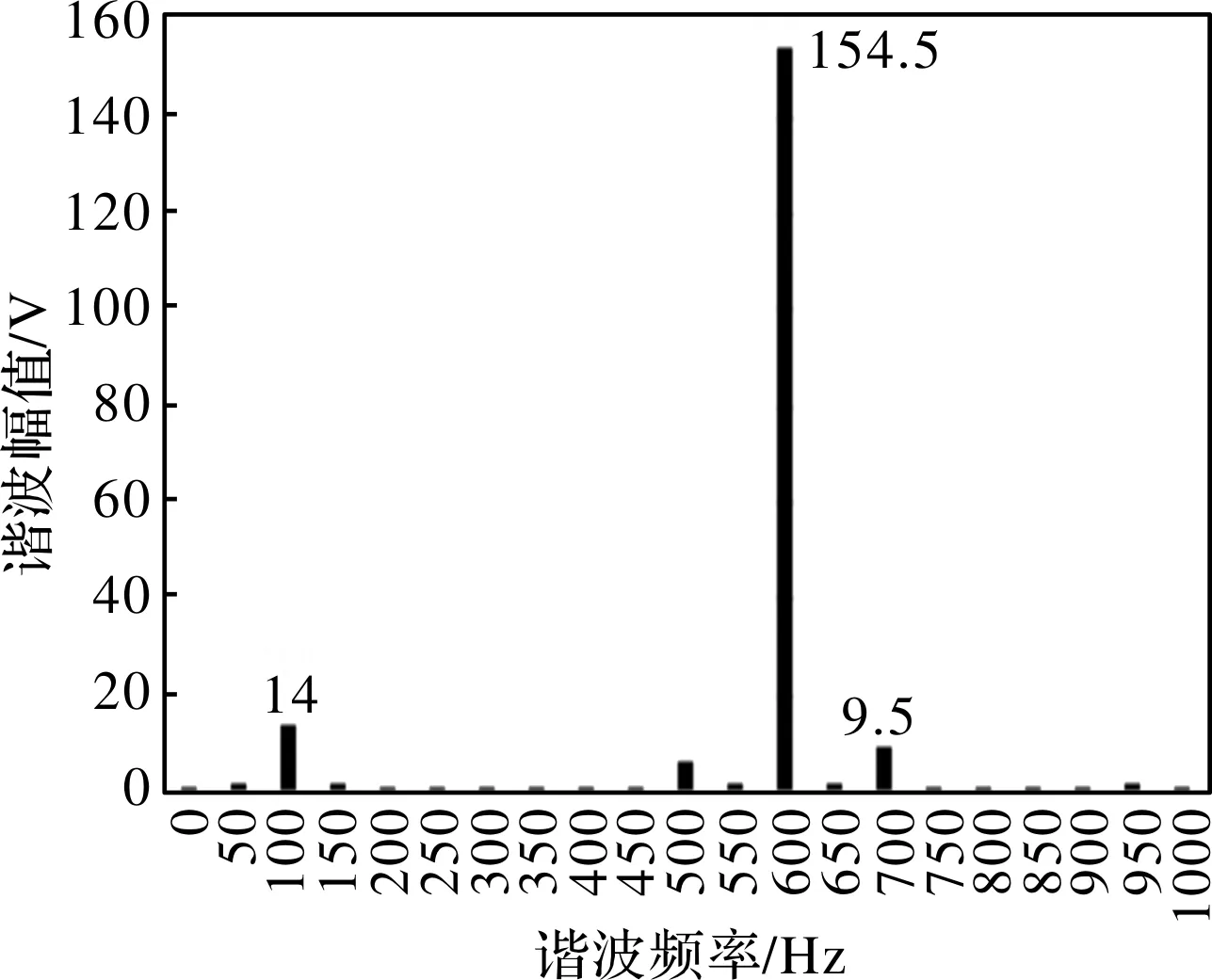
图10 FA1直线发电机的感应电势频谱图(定子电流1800 A)

对其它直线发电机感应电势频谱分析，得到其对应的感应电动势峰值如表1所示。

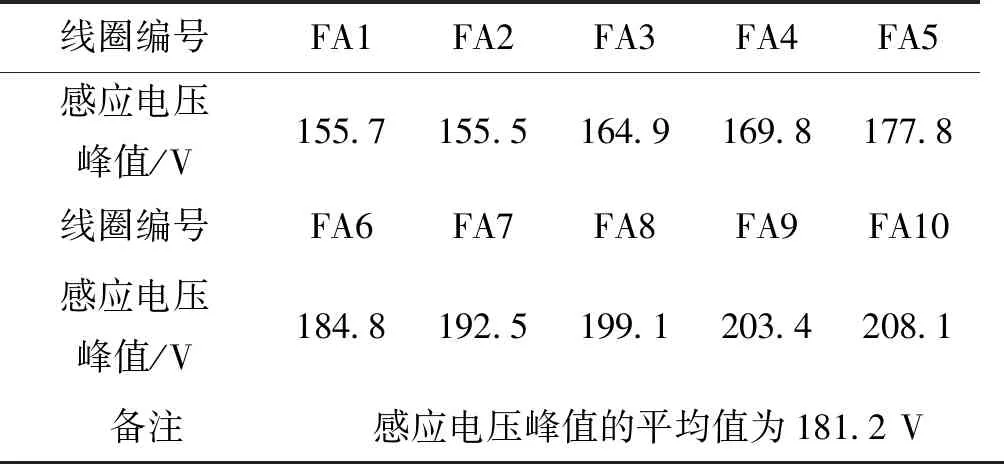
表1 不同直线发电机的感应电动势(定子电流1800 A)

3.1.2 定子电流为0 A时

定子电流为0 A时，仅动子磁极通入电流，因此，发电线圈感应电动势只与动子磁场相关。

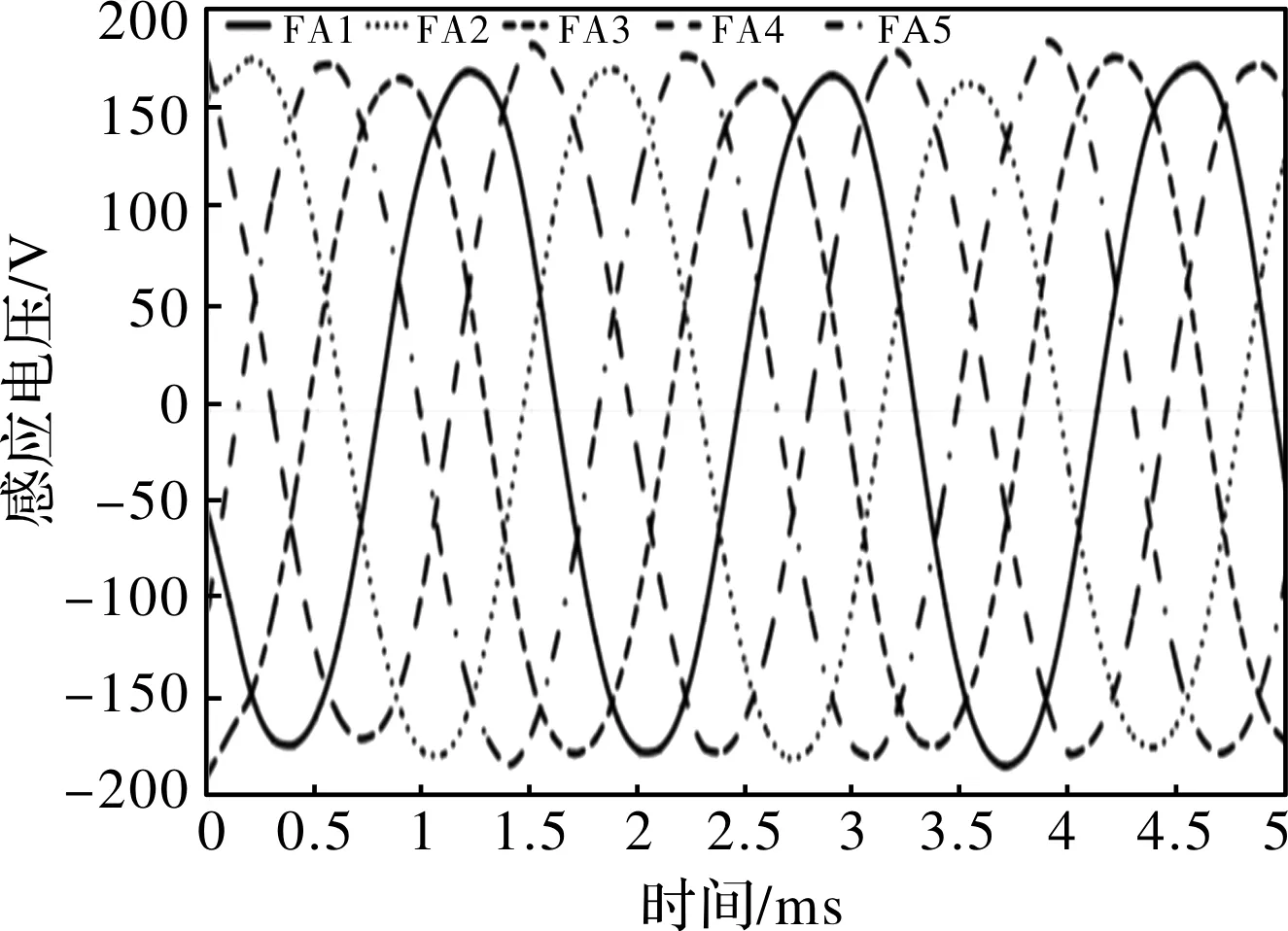
图11 左侧5个直线发电机的感应电势波形图(定子电流0 A)

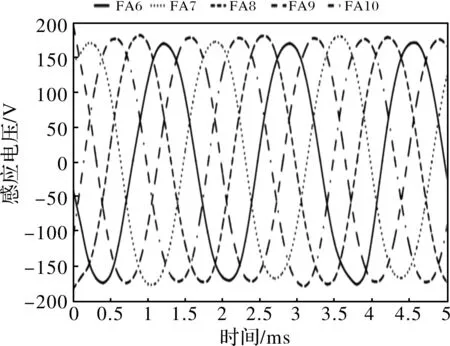
图12 右侧5个直线发电机的感应电势波形图(定子电流0 A)

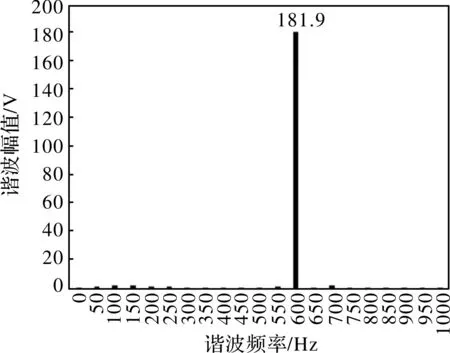
图13 FA1直线发电机的感应电势频谱图(定子电流0 A)

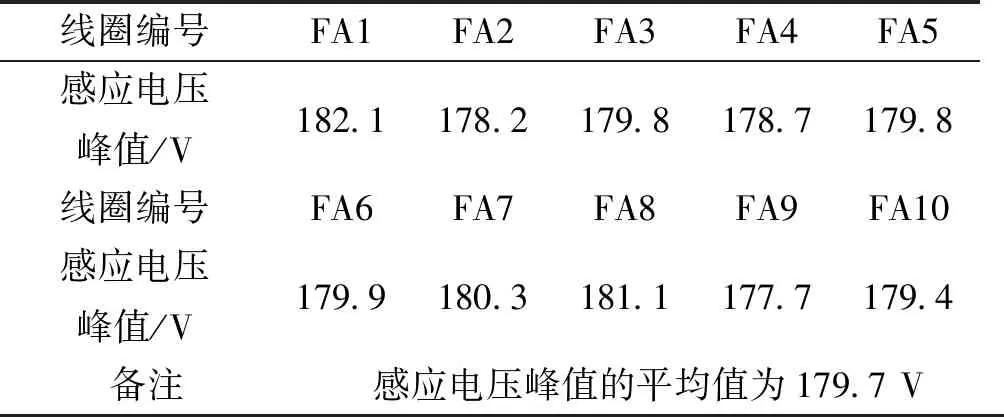
表2 不同直线发电机的感应电动势(定子电流0 A)

由表2可得，仅动子通电工况下所得各个直线电机的感应电动势大小相差较小，且感应电压峰值的平均值大小与表1的定子动子均通电工况基本一致。

3.1.3 结果分析

根据表1和表2的各个直线发电机感应电势大小对比分析，位于中间位置的FA5和FA6磁极的内嵌直线发发电机受定子磁场影响很小，而从中间往两侧，受影响依次增大，最外端FA1和FA10直线发电机受定子磁场影响最大。

有限元仿真结果与理论分析结论保持一致，说明不同位置的直线发电机受定子磁场影响均不同，即其感应电动势大小均不同。

3.2 定子电流对感应电动势的影响

前面节分析了定子磁场对直线发电机感应电势的影响，该节分析定子磁场的强弱对直线发电机感应电势的影响。通过定子电流分别为1300 A、1500 A、1800 A三种情况仿真分析，电流频率和磁极励磁电流均保持相同。各个直线发电机的感应电势如表3所示。

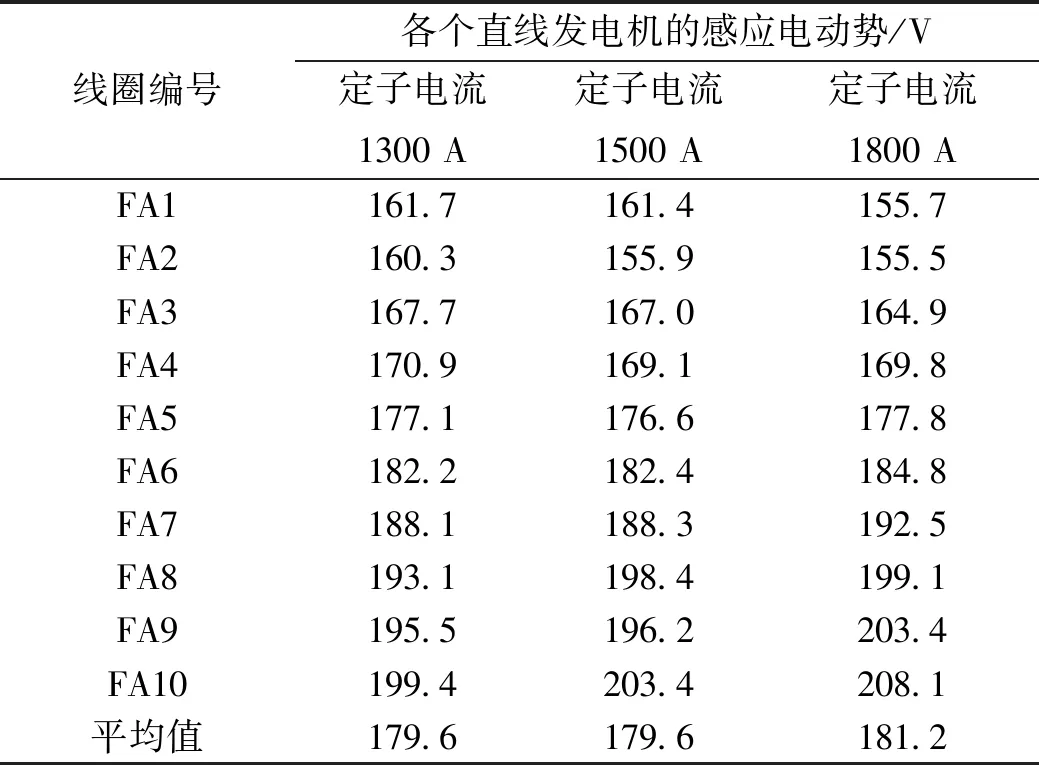
表3 定子电流大小不同情况下的直线发电机感应电动势

由表3可得，中间位置磁极内嵌的直线发电机感应电势受定子电流影响小，而左侧端部磁极的直线发电机的感应电动势随着定子电流增大依次减小，右侧端部磁极的直线发电机感应电动势随着定子电流增大依次增大。

3.3 车辆运行速度对感应电动势的影响

考虑不同运行速度时发电线圈感应电势，采用定子无电流的有限元模型，仿真得到不同速度对应的感应电势平均值，结果如表4所示。

表4 不同车辆速度对应的直线发电机感应电动势

由表4可得，直线发电机感应电动势峰值的平均值与车辆速度之比例大概为0.968，且随着速度增大而增大。根据资料，上海磁浮线直线发电机的空载电压为0～350VAC，频率为0 Hz～1615 Hz。表中，500 km/h速度对应电压峰值为483.5 V，其有效值为341.9 V，说明仿真结果比较准确。

3.4 气隙对感应电动势的影响

车辆正常运行时，气隙受轨道平整度影响是在时时波动，而此时车辆重量不变，气隙变化则磁极励磁电流也会实时调整。因此仿真分析了机械间隙分别为8 mm、9 mm、10 mm的工况直线发电机感应电动势，结果如表5所示。

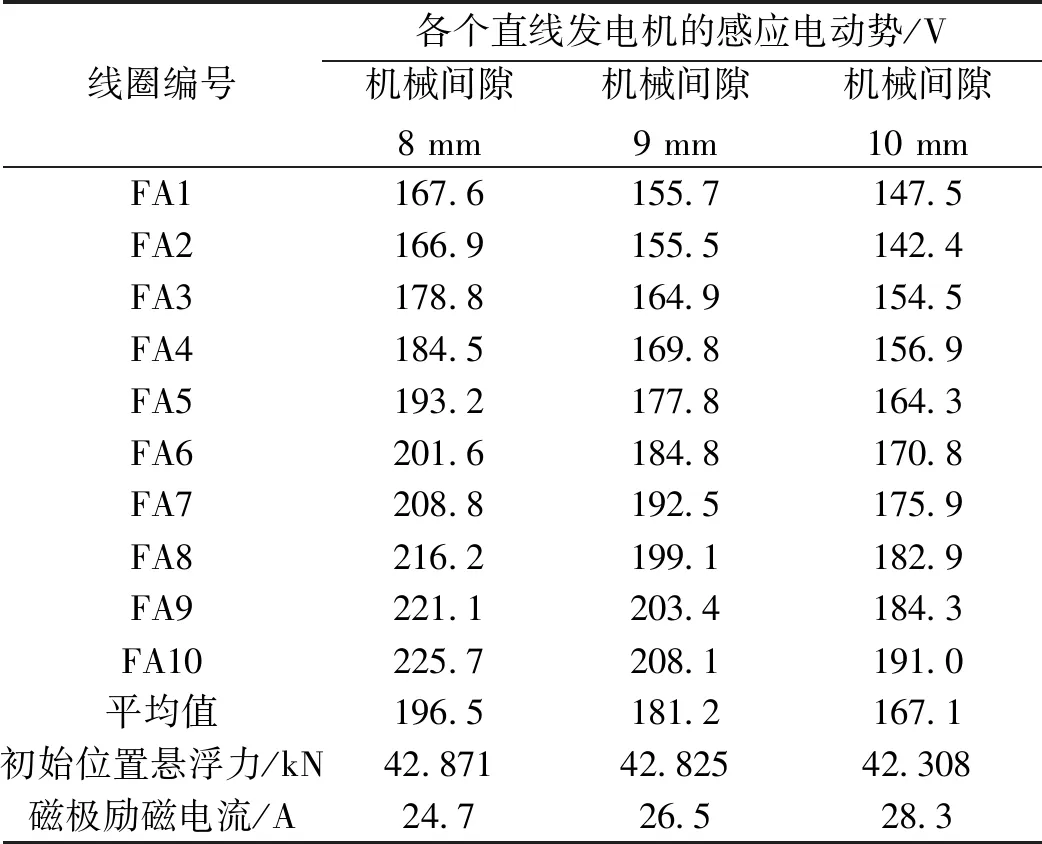
表5 不同机械间隙时直线发电机感应电动势

由表5可得，在车重不变的情况，即悬浮电磁铁所产生悬浮力不变，当气隙增大时，各个直线发电机的感应电势相应减小。

对于悬浮力不变的不同气隙工况，即I/δ为常数，将该式代入式(5)或者式(6)可知，感应电动势与气隙大小成反比关系，即该仿真结果与理论分析相符。

3.5 载荷对感应电动势的影响

车辆运行时，由于站点载客变动导致车辆重量发生变化，悬浮电磁铁磁极励磁电流也会相应调整。因此仿真分析了不同载荷工况时直线发电机感应电势值，结果如表6所示。

表6 不同车辆载荷时直线发电机感应电动势

由表6可得，从AW0到AW3载荷，随着车辆总重量增加，悬浮电磁铁励磁电流也增大，相应地气隙磁密也增大，因此直线发电机的感应电动势也增大。

4 结 论

本文介绍了安装于中高速磁浮长定子直线同步电机动子——悬浮电磁铁中直线发电机的感应发电原理，通过等效磁路的方式分析了两个特殊位置处直线发电机的感应电动势表达式，仿真分析了定子磁场、定子电流、车辆运行速度、气隙、车辆载荷等各个影响因子对不同位置的直线发电机感应电动势的影响，并得出以下结论：

(1)不同位置处直线发电机的感应电动势大小均不相同。沿运动方向，不同位置处直线发电机电动势值依次增大，中间位置的直线发电机受定子磁场影响最弱，两端位置的直线发电机受定子磁场影响最强。

(2)定子电流增大，中间位置的直线发电的感应电动势变化较小，而两端位置的直线发电机的感应电动势随着电流增加而相应增大或者减小。

(3)车辆运行速度越快，则直线发电机感应电动势越大，且电压峰值的平均值与车辆速度成近似线性关系，比例大概为0.967 V/(km/h)。

(4)车重不变，直线发电机的感应电动势随着气隙增大而减小。

(5)车辆载荷增加，即气隙磁场增大，直线发电机的感应电动势也随着变大。

以上分析结论可为中高速磁浮列车直线发电机系统的设计提供一定的理论参考。