一种多振子电磁式人体动能收集器研究

吕磊豪，杨 静，张国平，王 超，盛浩云

(1.中国人民解放军陆军勤务学院军事设施系，重庆 401331；2.中国人民解放军32733部队临汾军事代表室，山西 临汾 041000)

0 引 言

随着电子设备的微型化、集成化发展，越来越多的低功耗电子设备的出现，微能源技术的应用范围越来越广泛，人们日渐重视微能源技术的发展。微能源技术作为从外界环境中获取能量的技术，具有清洁、高效、可再生等特点。利用能量收集技术将外界环境中的能量转换为电能是解决微机电系统(Micro-Electro-Mechanical System，MEMS)等低功耗电子设备供电的可行方法[1]。

人体在活动中消耗巨大的能量[2]，在进行快跑时功率可达1630W。如果能加以利用，将是一种具有广阔前景的可再生能源。近年来，人体动能主要通过压电、电磁、摩擦电和静电等[3]能量转换方式转化为电能，为微型电子设备供电。虽然各种转换方式都有其特点，但电磁式能量收集结构因为其制作简单，收集功率大、使用寿命长、振动响应频率低[4]等优点，仍然是人体动能收集的重要方式。

为了提高电磁式人体动能收集器的输出功率，增加谐振频带，降低能量收集频率，使之更适应人体低频运动状态，大量学者展开了广泛研究。Miah A.Halim[5]等人提出了一种手摇式电磁能量收集器，通过机械冲击将人体的低频振动转换为高频振动，在5 Hz频率的激励下可收集2.15 mW的能量。Kangqi Fan等[6]人提出了一种单稳态电磁能量收集器，所提出的收集器具有单稳性，当激励水平越增大时，收集器工作频率会向低频移动。在9Hz频率的激励下的功率收集1.15 mW。K Pancharoen等[7]人提出了一种基于磁体阵列的磁悬浮电磁振动能量收集器，通过磁体阵列和磁悬浮等结构来扩展操作带宽，提高装置的功率输出，在行走和跑步过程中，装置置于髋关节时能量输出分别为5.35 μW和41.36 μW。Lin-Chuan Zhao等[8]人设计了提出了一种带有磁性轨道的电磁能量采集器，利用多重磁场的合理布置，形成均匀的圆形低势轨道。在频率为10 Hz，振幅为20 mm的激励时收集到0.33 mW的能量。吴子英等人[9]提出了附加非线性振子的双稳态电磁式振动能量捕获器。数值仿真表明：附加非线性振子的双稳态振动发电系统的响应幅值及功率密度均明显高于单一双稳态振动发电系统。

尽管电磁式能量转换结构已经较为完善，但现有能量收集器谐振频率大多仍然较高，在收集低频人体运动产生的能量时功率仍然较小，输出特性还有待提高。为了增大低频人体运动时能量收集的功率，本文设计了一种多振子电磁式人体动能收集器，减小了谐振频率，提高了低频人体运动时收集的能量。

1 能量收集器结构及物理模型

1.1 结构设计

本文设计的多振子电磁式人体动能收集器模型结构如图1所示。收集器由上、下端磁体振子、中心磁体(悬浮磁体)振子、三个线圈、上、下两端的弹簧和一个abs圆柱型空心管构成。上、下两个轴向充磁的永磁体振子和两端的弹簧相连接，中间反向充磁的永磁体振子在上下两个磁体的作用下悬浮在管中形成悬浮振子，其中悬浮振子由两个永磁体和两片黑色垫片组合而成。此外，在悬浮振子表面包裹油性薄膜来降低振子与管壁之间的摩擦，减少能量损失。两端的弹簧由上下两个端盖固定，其中弹簧和磁铁与上下端盖之间均为粘性连接。在受到振动激励时，上中下三个永磁体振子均在激励的作用下做上下往复运动，通过线圈内磁通量变化产生感应电势，完成从机械能到电能的转换。

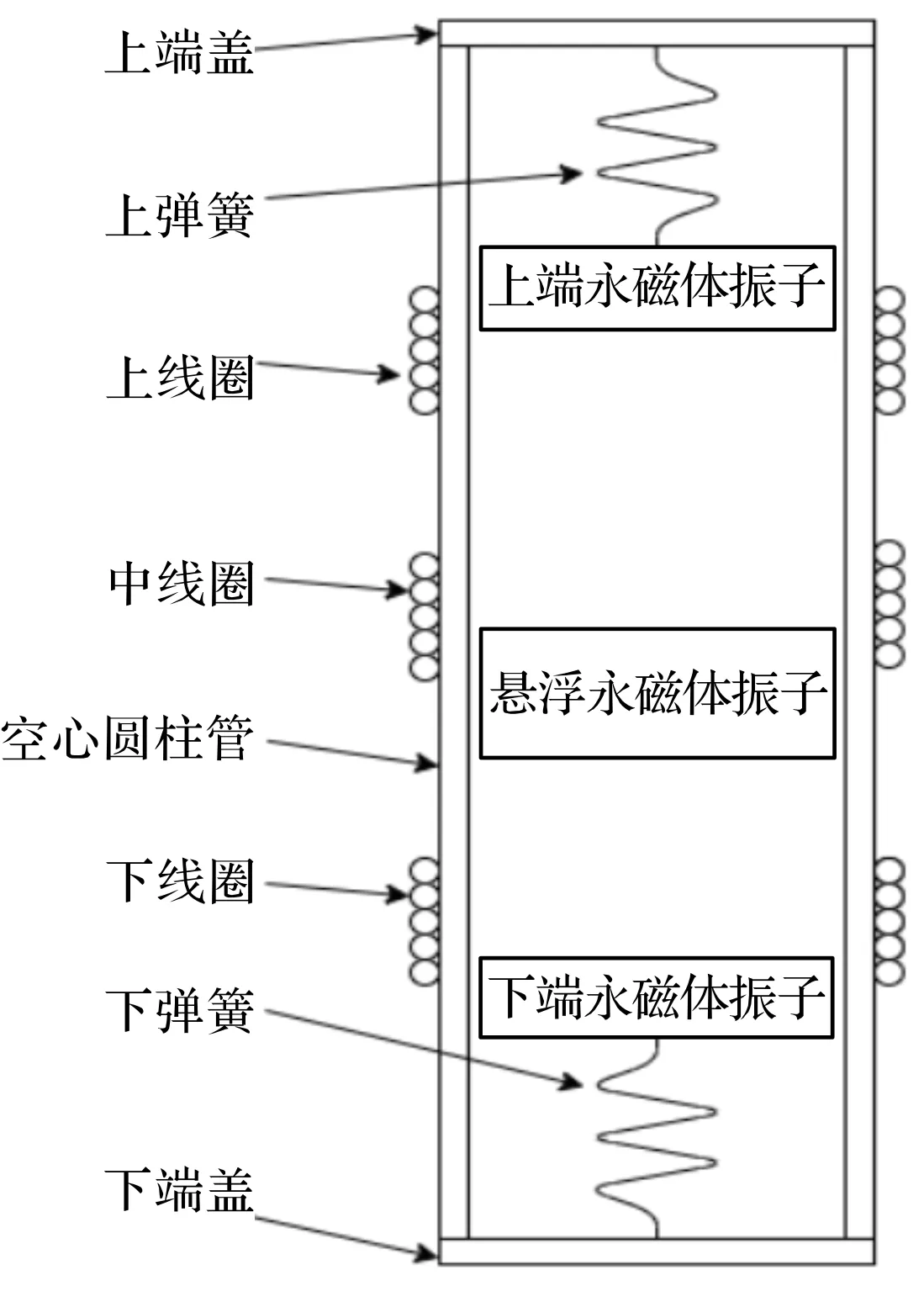
图1 多振子电磁式人体动能收集器结构图

1.2 系统物理模型

该多振子电磁式人体动能器物理模型如图2所示。为了方便能量收集器的建模，将收集器下端盖外表面圆心作为笛卡尔坐标系的原点，x1(t)、x2(t)、x3(t)分别是质量块m1、m2、m3的绝对振动位移，z(t)为激励源简谐振动位移，设z(t)=A0sinωt,A0为振幅，ω为频率，则ui(t)=xi(t)-z(t)为振子相对位移。令向上运动为正方向，多振子电磁人体动能收集器机电耦合振动微分方程[10]为

(1)

式中，mi、ci(i=1,2,3)分别对应上、中(悬浮振子)、下振子质量和阻尼系数。k1、k3分别为上下两端弹簧的刚度系数，k2为悬浮振子系统磁弹簧等效刚度系数。Fm1、Fm2、Fm3分别为上中下振子受到磁力的轴向分量。

(2)

式中，γ1、γ2、γ3分别为各振子系统等效电磁耦合系数。Ri、RLi、Lci、Ii(i=1,2,3)分别为上中下线圈内阻、负载电阻、电感和输出电流。

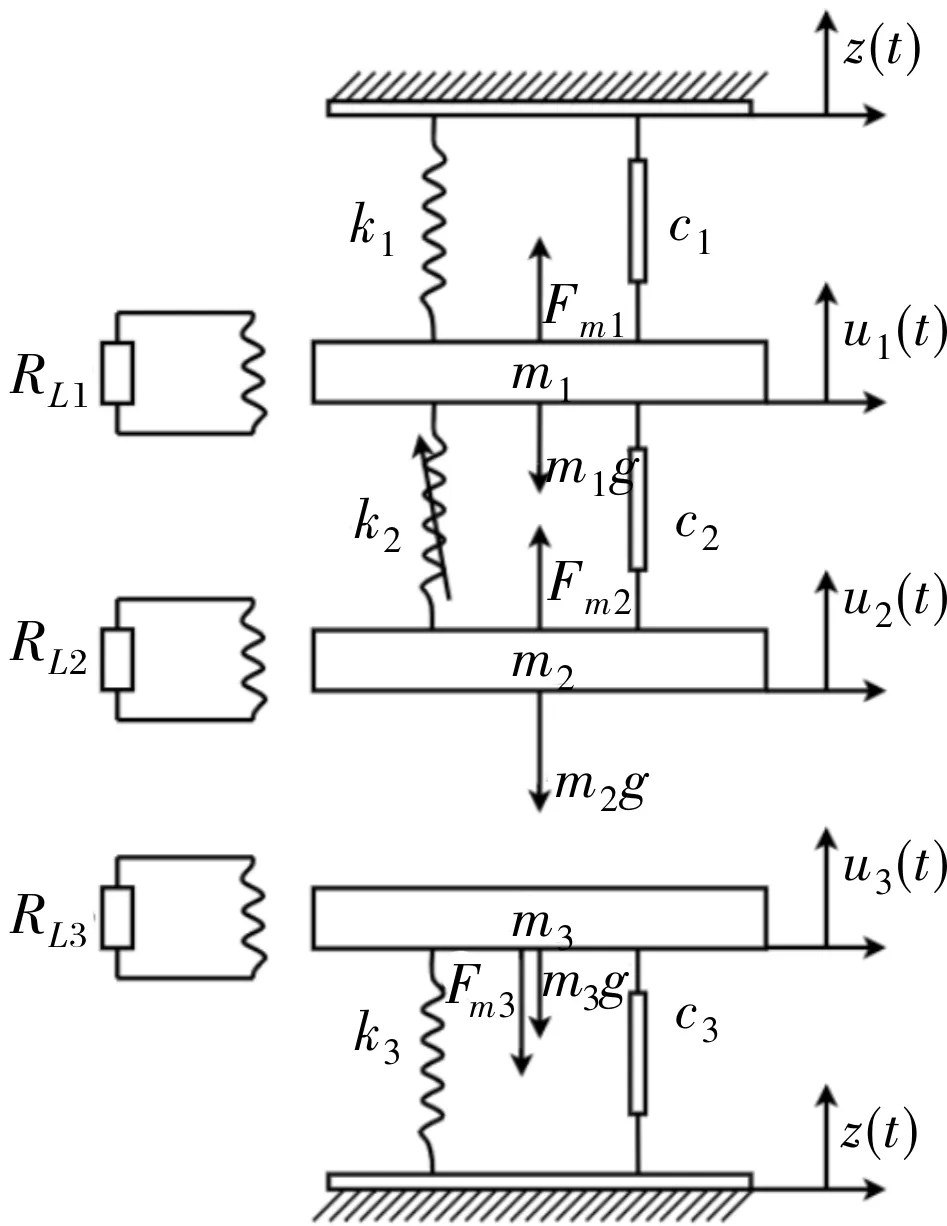
图2 动能收集器物理模型图

当收集器受到外界激励时，各振子将在管内做上下往复运动，此时永磁体振子之间受到相互的磁力作用。对于中心磁体m2(悬浮磁体)，受到的磁力主要来自上、下两个磁体m1、m3的排斥作用，悬浮振子受到的磁力大小为

Fm2=Fm1-Fm3

(3)

为了得到不同距离时永磁体受到的磁力大小，对圆柱型磁体在不同距离时的磁力大小进行实验测量，结果如图3所示,由图3(a)可得，在距离为0.116 m时磁力约为0 N，所以在考虑两端永磁体受力时忽略了另一端永磁体带来的磁力作用。因此，上端永磁体振子受到的磁力大小为Fm1，下端永磁体受到的磁力大小为Fm3。根据实验测量，中心磁体m2(悬浮磁体)所受磁力大小如图3(b)所示。

图3 永磁体振子受力大小曲线

从图3(b)可以看出悬浮振子受力与位移大致满足线性关系，可根据胡克定理得到悬浮振子的磁弹簧弹性系数k2[11]：

(4)

2 磁场仿真

使用Ansys Electromagnetics Suite 18.0建立磁体有限元仿真模型，得到初始位置网格划分图和磁感应强度云图，如图4所示，其中悬浮振子距上、下端振子初始距离分别为69 mm和42 mm，各振子均采用厚度5 mm，半径15 mm，矫顽力HC=-890 kA/m，剩余磁感应强度Br为0.25 T的圆柱形永磁体。

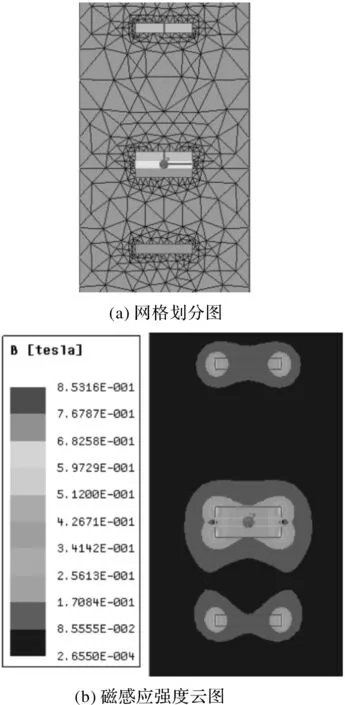
图4 初始位置磁场分布图

对于该能量收集器，线圈的感应电势主要由穿过线圈平面磁通量的变化率决定，而电磁力的大小与磁场强度的轴向分量有关。使用Ansys Electromagnetics Suite 18.0中的场计算器分别对轴向磁感应强度Byi和磁通量Φi(i=1,2,3)分别为上、中(悬浮振子)、下振子的轴向磁感应强度和线圈的磁通量。进行仿真计算，为下一步Simulink系统仿真提供磁场参数。永磁体振子轴向磁感应强度和线圈平面磁通量与振子相对位移的关系曲线如图5、图6所示。

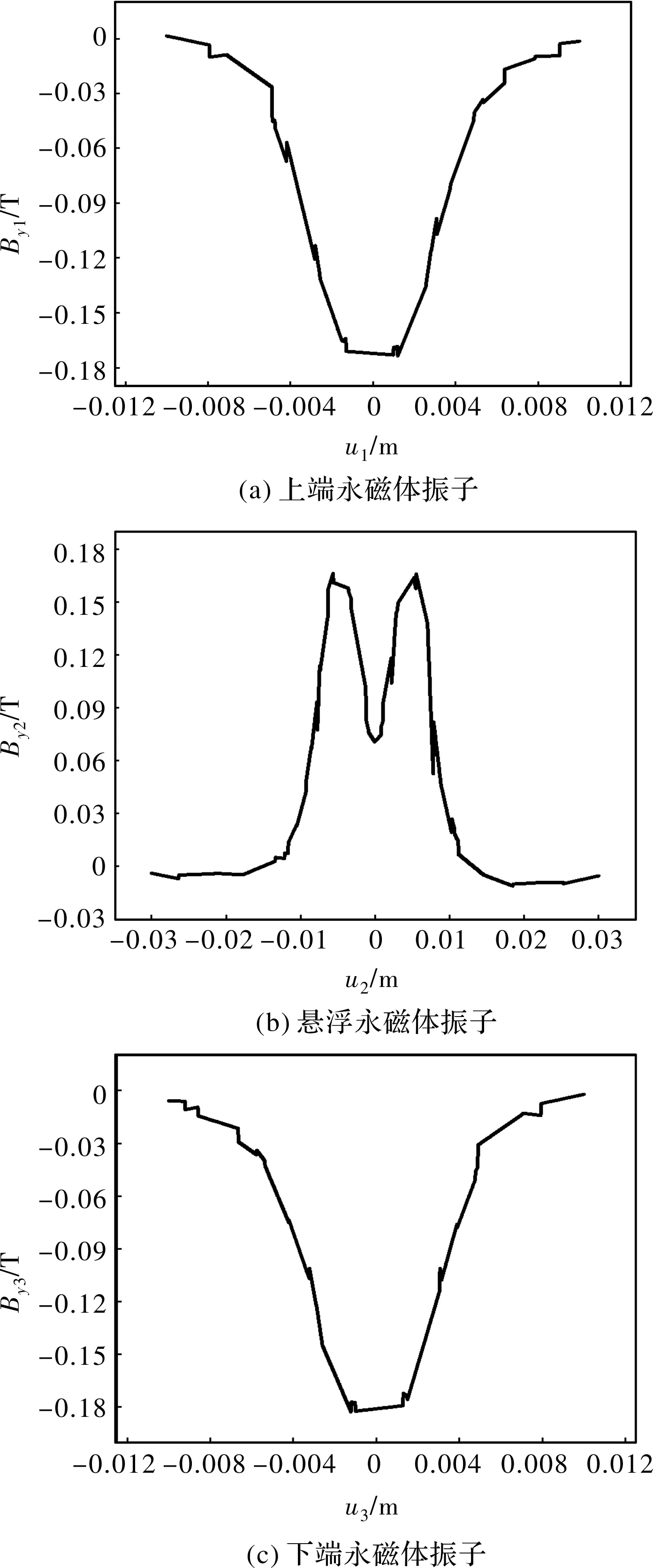
图5 永磁体振子轴向磁感应强度随距离变化曲线

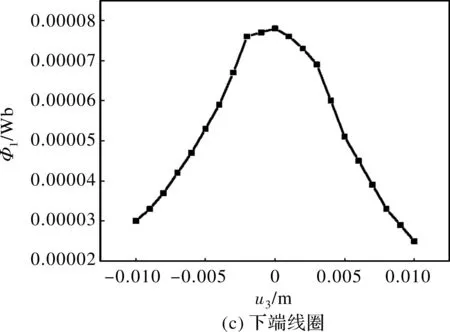
图6 线圈平面磁通量与距离的关系曲线

3 系统仿真

3.1 建立Simulink系统仿真模型

对式(1)建立的电磁式能量收集器振子的运动微分方程进行拉氏变换，可以得到能量收集器在工作时的各振子位移的s域函数为

(5)

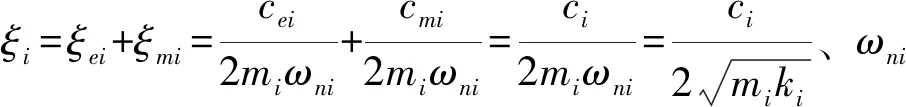
(6)

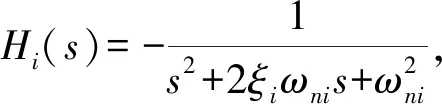
(7)

对于能量收集装置，根据电磁感应定律，线圈产生的电动势可以表示为[12]

(8)

当装置接入负载时，线圈中流过电流，会与永磁体产生电磁力，电磁力表达式为

(9)

根据式(5)～式(9)利用Simulink进行系统模型仿真，并将表1的参数带入仿真模型中，得到仿真结果。该电磁式能量收集器Simulink仿真模型如图7所示。参数如表1所示。

图7 Simulink系统仿真模型

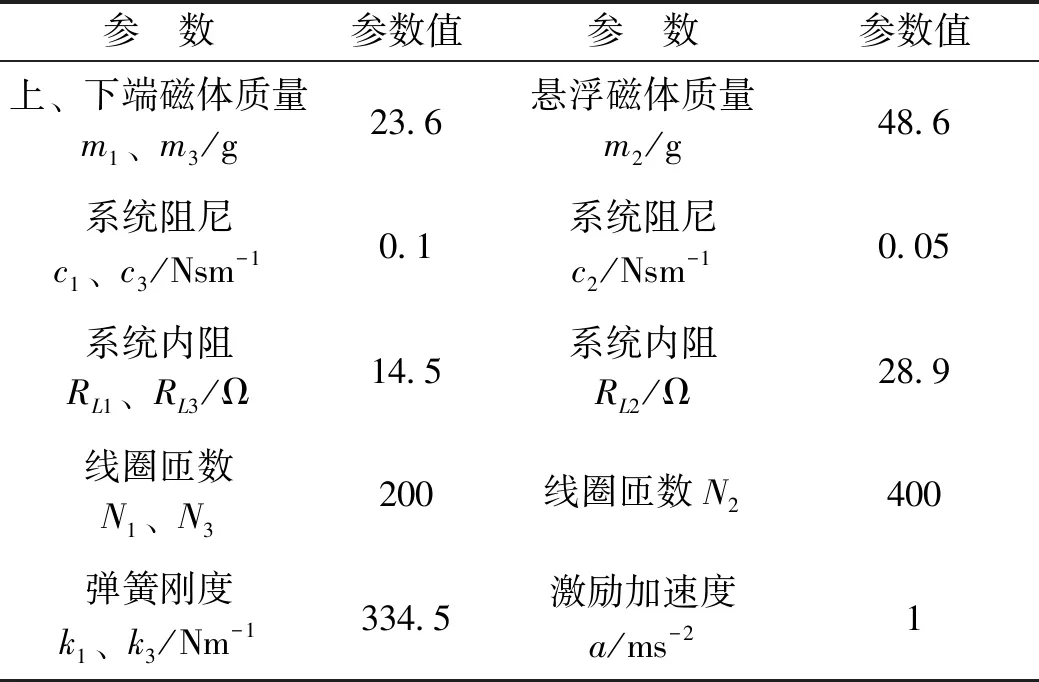
表1 多振子电磁式人体运动能收集器系统参数

3.2 仿真计算

通过Simulink系统仿真计算了1～25 Hz不同频率激励时能量收集器空载输出电压Voci和振幅Ai的大小，其中(i=1,2,3)分别对应上、中(悬浮振子)、下振子。如图8所示，由图8(a)、图8(c)可知，上、下端振子系统约在激励频率为19 Hz时达到谐振频率，其系统空载电压Voc1、Voc3最大分别为0.032 V、0.075 V,振幅最大值分别为0.356 mm、0.349 mm。因受到磁力的大小不同，产生的电压幅值存在差异。如图8(b)所示，悬浮振子系统大约在激励频率为5 Hz时达到谐振频率，开路电压Voc2可达1 V,振幅最大值约为10 mm。各系统在谐振频率激励下的空载电压波形曲线如图9所示，图9(a)中输出电压波形在0 V电压处出现小幅度抖动，为悬浮振子轴向磁感应强度By2曲线出现波动导致。

图8 空载电压和振幅随激励频率变化曲线

图9 共振激励频率下的空载电压波形

为了得到最优负载的大小，对该装置5 Hz、19 Hz两个谐振频率点外接负载时的输出功率进行仿真实验，因为激励频率较低，所以在仿真时忽略了电感的大小。输出功率随负载电阻变化的曲线如图10、图11所示。由图10可得，当激励频率为5 Hz时，悬浮振子系统最优负载RL2为29 Ω左右，最大瞬时功率为7.3 mW。由图11可得，当激励频率为19 Hz时，上、下端振子系统最优负载大小RL1和RL3均为15 Ω左右，最大瞬时功率P1和P3分别为18.2 μW,93.9 μW。

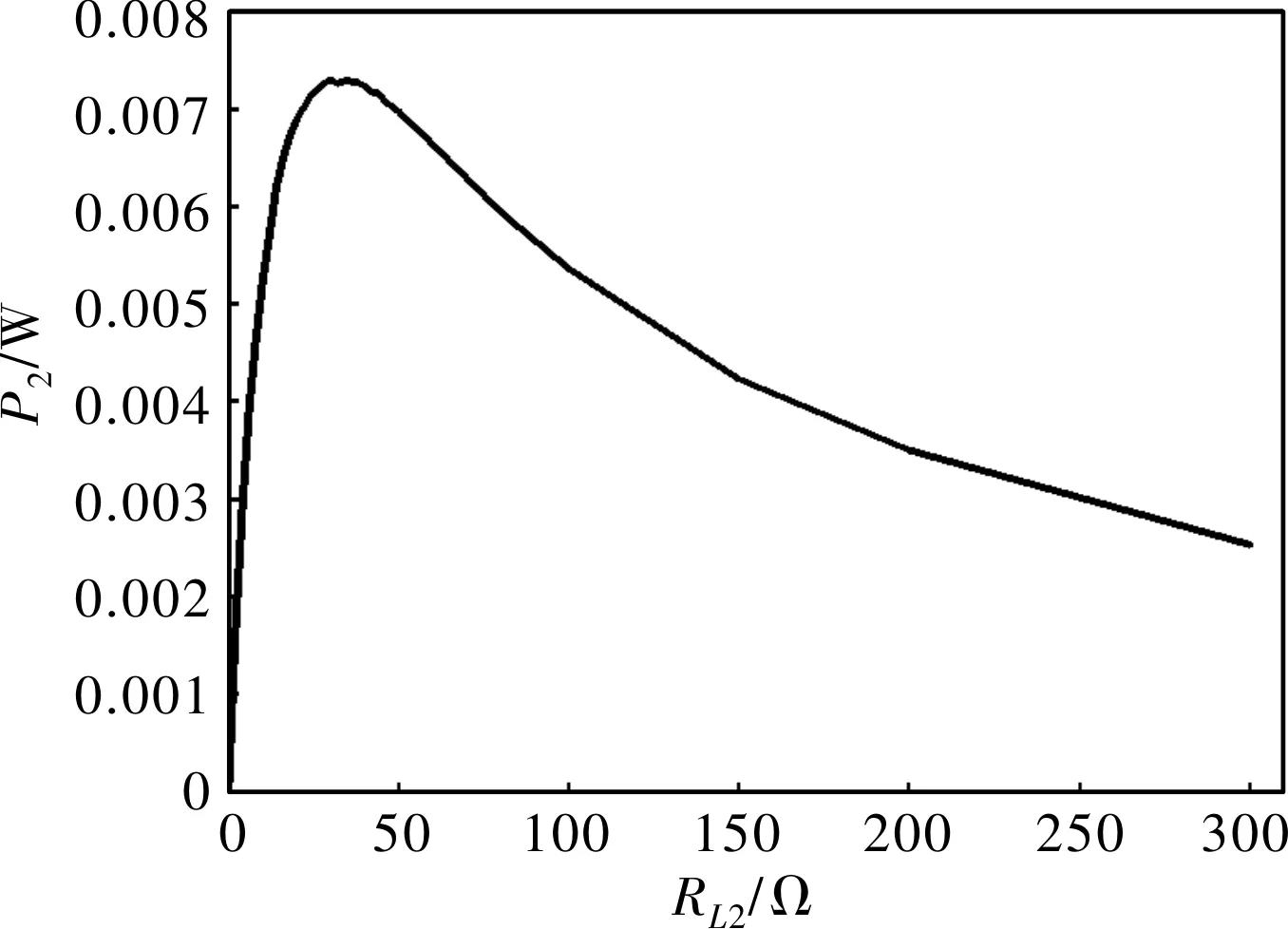
图10 5 Hz激励频率时悬浮振子系统瞬时功率随负载变化曲线

图11 19 Hz激励频率时瞬时功率随负载变化曲线

由文献[13]可知，人体运动时身体各部位得加速度远大于1 m/s2，为了更加贴合人体运动实际，对不同加速度时2～5 Hz频率下悬浮振子系统空载电压进行仿真，如图12所示。由图12可知，加速度与空载电压基本呈正比关系。在激励加速度为10 m/s2时，2～5 Hz频率下空载电压Voc2分别可达0.73 V、1.16 V、3.41 V和8.2 V。

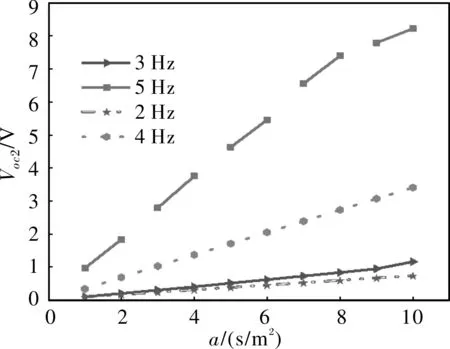
图12 不同加速度时2～5 Hz频率下悬浮振子系统空载电压曲线

4 实验与分析

4.1 实验样机制作

所设计的能量收集器样品如图13所示，采用abs材料制作样品外壳，在减少装置重量时保证结构的强度。该收集器模型总高度为170 mm，总质量为121.3 g，圆柱管内外径分别为31 mm和37 mm，弹簧初始长度25 mm，永磁铁尺寸为30×5 mm，黑色垫片尺寸为30×2 mm。另外，为了更好的收集能量，据文献[5]研究，线圈初始位置应与磁体重合40%。因此由下至上分别在28～43 mm、74.4～99.4 mm、123～138 mm处设置长分别为15 mm、30 mm、15 mm的凹槽，以便于线圈位置的固定。

图13 能量收集器样机和组成部件

4.2 人体动能收集实验结果与分析

将收集器置于身高为1.7 m，体重为65 kg的实验者手掌、背包侧袋(如图14所示)，在实验过程中尽量保持收集器与地面垂直放置，减少磁体与管壁的摩擦，利用UT4062C示波器测量收集器总的空载电压Voc。在实验时得知，在1～5 Hz时上、下端振子系统输出电压远小于悬浮振子系统，所以在进行实验时暂不考虑上、下端输出电压。即总的空载电压Voc为悬浮振子系统空载电压Voc2。如图15所示为实验者分别以3～12 km/h的速度运动时装置的空载电压峰值大小曲线。由图15可知，空载电压峰值随运动速度的增加而增大，在6 km/h时有较为显著的提升，原因是当实验者速度为6 km/h时，实验者由步行变成跑步，收集器受到的加速度有较大的增强。当速度达到12 km/h时，空载电压峰值Vm在手掌和背包侧袋处分别达到1.23 V、0.97 V。由于装置在背包侧袋受到摩擦增大和不规则的晃动使振子加速度减小，所以空载电压峰值较位于手掌时稍低。

图14 装置的佩戴方式

图15 不同速度下空载电压峰值变化曲线

当实验者以10 km/h和6 km/h的速度运动时，手掌和背包侧袋产生的空载电压波形如图16、图17所示。

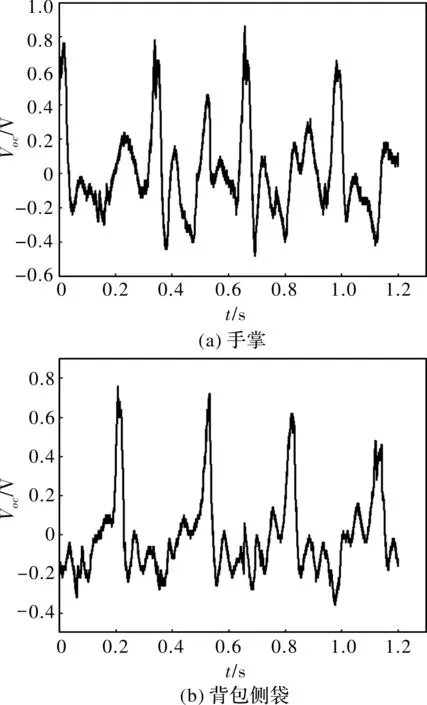
图16 10 km/h速度下装置在不同位置的电压波形图

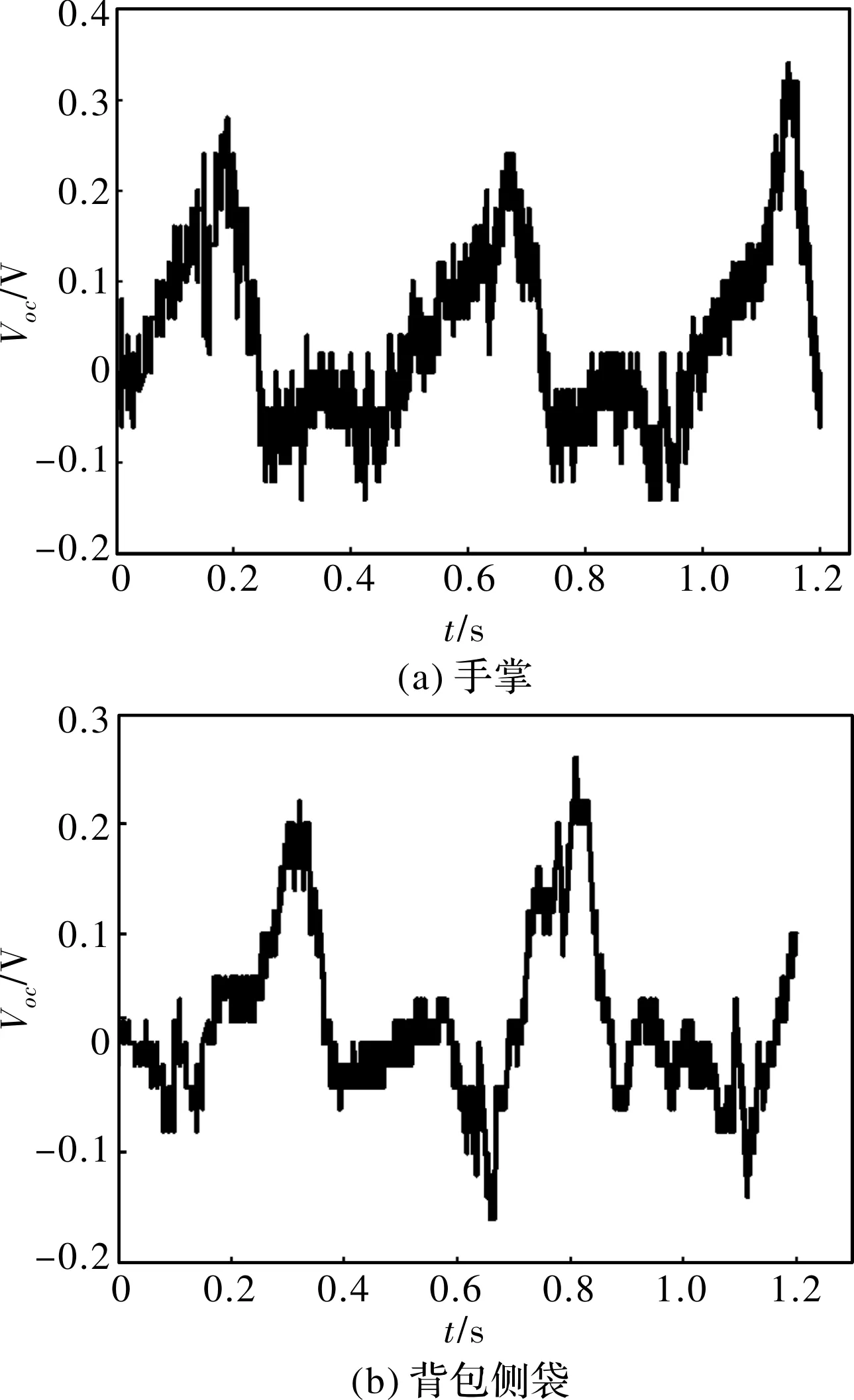
图17 6 km/h速度下装置在不同位置的电压波形图

由图16可知，实验者以10 km/h的速度运动时，在手掌、背包侧袋处空载电压分别为0.82 V、0.78 V，能量收集器工作频率约为3.3 Hz。由图17可知，实验者以6km/h的速度运动时，在手掌、背包侧袋处空载电压分别为0.315 V、0.248 V，能量收集器工作频率约为2Hz。运动时收集器受到加速度约为5～7 m/s2，空载电压大小与图12仿真结果大致相符。当负载电阻为29 Ω，在10 km/h的速度运动时，手掌和背包侧袋收集的最大瞬时输出功率分别为6.47 mW、5.13 mW。收集功率与文献[6]相比提高了460%～560%。在6 km/h的速度运动时，收集的最大瞬时输出功率分别为0.78 mW、0.496 mW。

5 结 语

为了更好的收集人体运动时产生的机械能，为低能耗便携式电力电子设备提供电能，提出了一种多振子电磁式人体动能收集器，通过仿真结果可得该收集器存在5 Hz、19 Hz两个谐振频率和较好的低频运动能量收集功率，达到较为理想的状态。由人体运动实验可得，当实验者将收集器置于手掌和背包侧袋处以10 km/h运动时，可产生的瞬时最大输出功率为6.47 mW和5.13 mW，当实验者以6 km/h运动时，可产生的瞬时最大输出功率为0.78 mW和0.496 mW。根据实验数据可知，该多振子电磁式人体动能收集器在收集低频人体运动时有较好的输出特性，相比文献[5-8]有一定程度的提升。在后续研究中可通过调整上、下端弹簧刚度来改变系统的谐振频率，使收集器更适应人体运动状态，进一步增加人体动能收集效率。