装配式建筑PC构件车辆调度优化
2022-11-10蒲坤俏
蒲坤俏, 万 鹏,2*
(1.青岛理工大学 管理工程学院, 山东 青岛 266525;2.青岛理工大学 智慧城市建设管理研究中心, 山东 青岛 266525)
0 引 言
以现浇为主体的传统建造模式施工效率低下,存在严重的资源浪费和环境污染问题,与我国倡导的绿色发展理念相背离。
近年来,政府大力支持装配式建筑发展,以降低资源环境压力,提高劳动生产效率。
装配式建筑所需的预制构件(Precast Concrete, PC)是工厂采用标准化方式生产,可减少不必要的材料浪费,更加节材环保,且减少了施工现场人员的配备,在用工成本和安全生产方面都有较大改进[1]。为了控制装配式建筑建造成本,刘炜[2]通过对比分析传统现浇模式及装配式建筑的成本构成,得出装配式PC构件的增量成本构成。
其中,PC构件制作人工成本、结构增量、购置税、装运存卸等成本较高,具有较大的优化空间。而PC构件配送成本的高低与车辆配送方案有较大关系,若对配送方案进行合理配置,可在一定程度上提高配送效率,降低配送成本。
目前,国内外针对装配式建筑PC构件配送成本优化的研究相对较少。Chan W T等[3]针对预制构件生产调度问题,提出一种流水车间排序模型,并使用遗传算法求解。Zhou Z等[4]设计了一种基于贪婪策略的改进遗传算法,并应用于云环境中的任务调度优化。段海宁等[5]通过构建基于车辆油耗成本、人工成本及车辆租赁成本的成本优化模型,并改进粒子群算法,得到最优成本下的车辆配送方案。但该模型未考虑工地的时间窗约束。邵必林等[6]考虑到配送过程中可能产生的时间等待成本,并基于时间窗约束构建配送成本优化模型,最后得到最优成本下的车辆调度方案。胡晓晨[7]在此基础上,将车辆运送过程中的道路交通阻抗因素考虑在内,并引入传统路阻函数(BPR)模型。但该模型是通过分析美国一些低饱和流量道路所得,当城市道路处于饱和或者过饱和状态时,模型的拟合精度较差[8]。
综合上述分析,文中在模型构建时考虑多车型、时间窗及道路交通拥堵情况,构建PC构件配送成本优化模型,设计遗传算法进行求解,并进行算例测算,验证该模型的有效性。
1 问题描述与条件假设
1.1 问题描述
假设有1个预制厂F和S(>2)个施工工地,预制厂配备有专门的运输车辆,根据载重量不同,分为λ种车型。预制厂需要根据工地配送需求,在各工地要求的时间窗(TEs,TLs)范围内送达。在此过程中,要求设计一套合理的配送方案,使得配送总成本最小。
1.2 条件假设
为了便于研究,将实际生活中的问题转化成可以求解的数学模型,做出以下假设:
1)配送车辆的行驶路线是提前规划好的最佳路线,即运输距离是已经确定的。
2)同一车型的车辆在仓库的装车时间、同一工地的卸车时间均相同。
3)在仓库装车时,同一构件一次只能向一辆车装车。
4)在工地卸车时,一次只允许一辆车进行卸车。
5)所有配送车辆在工地卸车完成后均需在第一时间返回预制厂,并等待下一批次的配送任务。
6)配送车辆不会出现中途故障停车现象,只会因道路交通拥堵产生等待时间。
7)配送车辆的油耗量只与其载重量、运输距离和时间有关,且成正比例关系。
2 模型构建
2.1 参数推导
车型为λ的车辆单次可运载构件数量
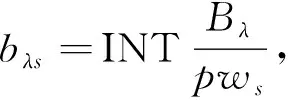
(1)
式中:INT----取整函数;
Bλ----λ车型载重量;
pws----单件构件重量。
车型为λ的车辆完成工地S所有订单需求量的配送总车次数
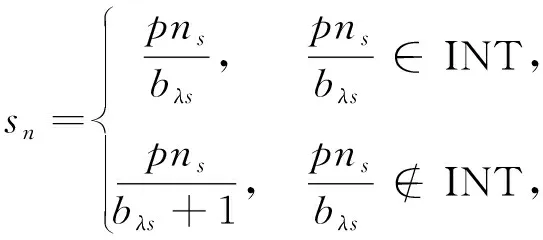
(2)
式中:pns----工地S所需构件总数量。
预制构件配送流程中涉及到的时间参数如图1所示。
各时间参数推导如下:
1)车辆因前一车次正在装车,而需等待的时间为
WBTsn=STsn-STsn-1-BTλ,
(3)
式中:STsn----当前车次发车时间;
STsn-1----前一车次发车时间;
BTλ----装车时间。
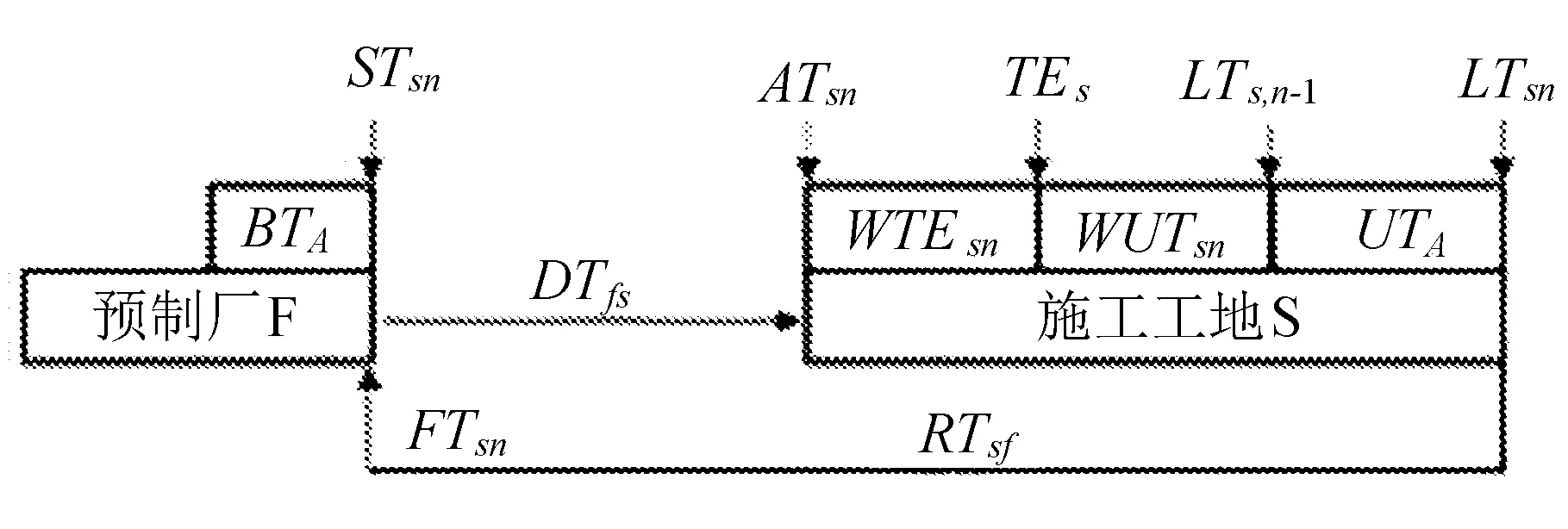
图1 预制构件配送流程时间参数
2)假设车辆在满载时的平均行驶速度为V1,则当交通畅通无阻的情况下,从预制厂F运输到施工工地S所需的时间为
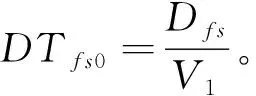
(4)
为使模型更具实际应用价值,文中考虑了车辆行驶过程中的道路交通阻抗因素。采用基于百度交通大数据计算得出的拥堵指数作为衡量城市道路交通拥堵程度的指标,更加符合不同城市的实际拥堵情况。拥堵指数计算公式为
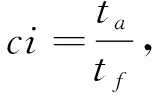
(5)
式中:ci----拥堵指数;
ta----实际通行时间;
tf----自由通行时间。
根据式(5)可以看出,实际通行时间为自由通行时间与拥堵指数的乘积,进而可求得存在道路交通阻抗因素的影响时,配送车辆从预制厂行驶至施工工地S的实际运输时间为
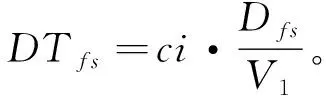
(6)
3)车辆到达工地的时间点
ATsn=STsn+DTfs。
(7)
4)车辆因到达工地的时间早于时间窗约束TEs而需要等待的时间
WTEsn=TEs-ATsn。
(8)
5)车辆到达工地时,因前一车次正在卸车而需要等待卸车的时间
WUTsn=LTs,n-1-ATsn,
(9)
式中:LTs,n-1----前一车次的离开时间。
6)车辆在工地的总等待时间
WTsn=p·WTEsn+q·WUTsn,
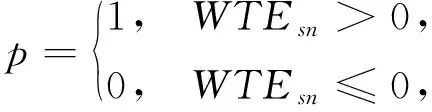
(10)
7)车辆离开工地的时间点
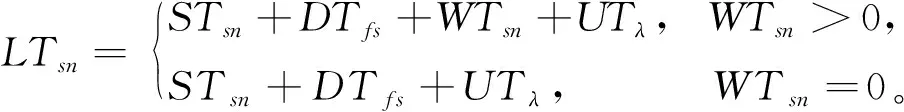
(11)
8)假设车辆返回时的空载运输速度为V2,则当存在道路交通拥堵情况时,从工地S返回到预制厂F所需的时间为
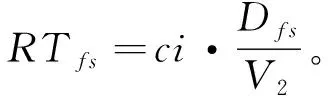
(12)
9)车辆返回预制厂的时间点
FTsn=LTsn+RTfs。
(13)
2.2 配送总成本
预制构件的配送成本可分为固定成本和可变成本。其中,固定成本主要包括配送车辆的租赁费、维护管理费、折旧费、人工费等;可变成本主要包括燃油成本,因仓库等待装车、工地等待卸车,在运输途中因交通阻抗因素导致的等待时间等产生的时间等待成本,以及未按照施工工地要求的时间窗约束配送的时间惩罚成本[9-10]。
2.2.1 固定成本
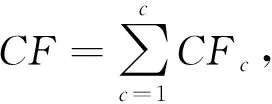
(14)
式中:CF----总固定成本;
CFc----单辆车固定成本;
c----车辆数。
2.2.2 燃油成本
假设每百公里油耗量为O(L),车辆平均时速为V(km/h),则行驶一百公里所需的时间t=100 km/h,单位时间油耗量为O/t。单位时间燃油成本为
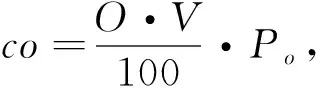
(15)
式中:Po----燃油价格。
总燃油成本
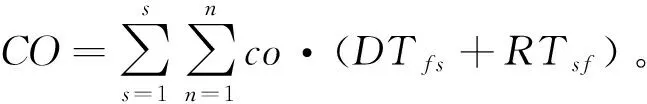
(16)
2.2.3 时间等待成本
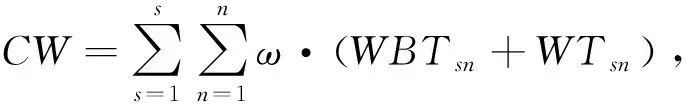
(17)
式中:ω----时间等待成本系数。
2.2.4 时间惩罚成本
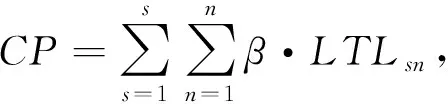
(18)
式中:β----时间惩罚成本系数。
2.2.5 配送总成本
配送总成本主要包括配送车辆固定成本CF、总燃油成本CO、时间等待成本CW和时间惩罚成本CP等。配送总成本可表示为
CT=CF+CO+CW+CP=
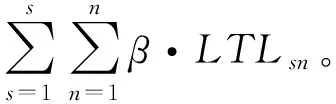
(19)
2.3 车辆调度成本优化模型构建
基于配送总成本最低的预制构件配送车辆调度优化模型
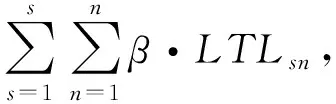
(20)
s.t.
STsn≥FT,
(21)
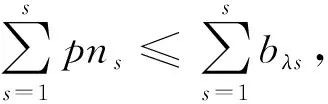
(22)
STsn-STs,n-1≥BTλ,
(23)
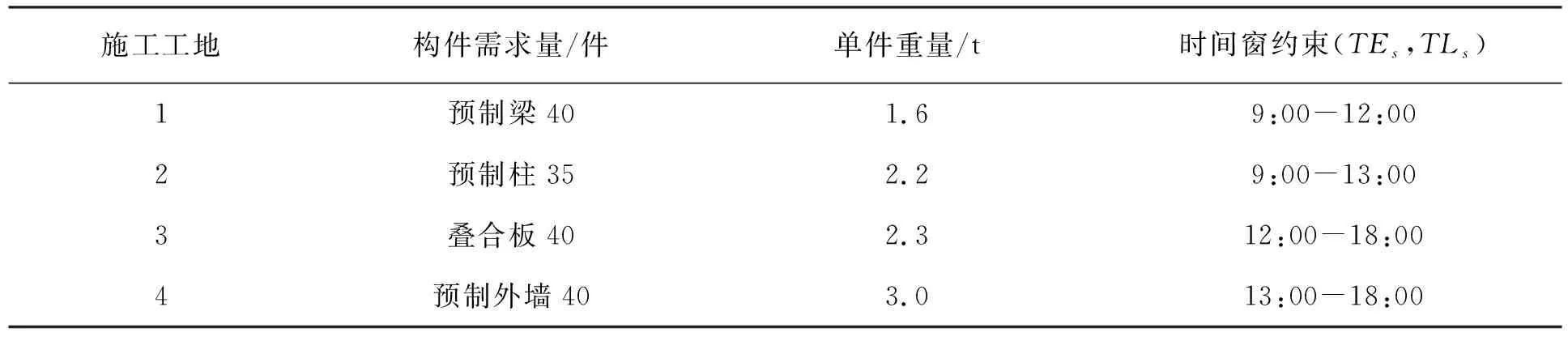
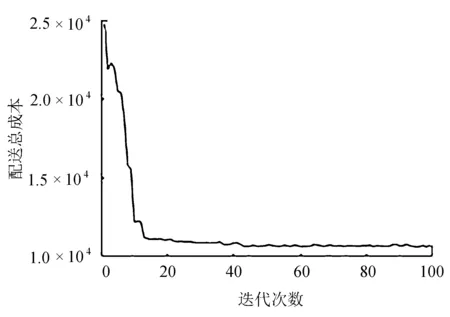
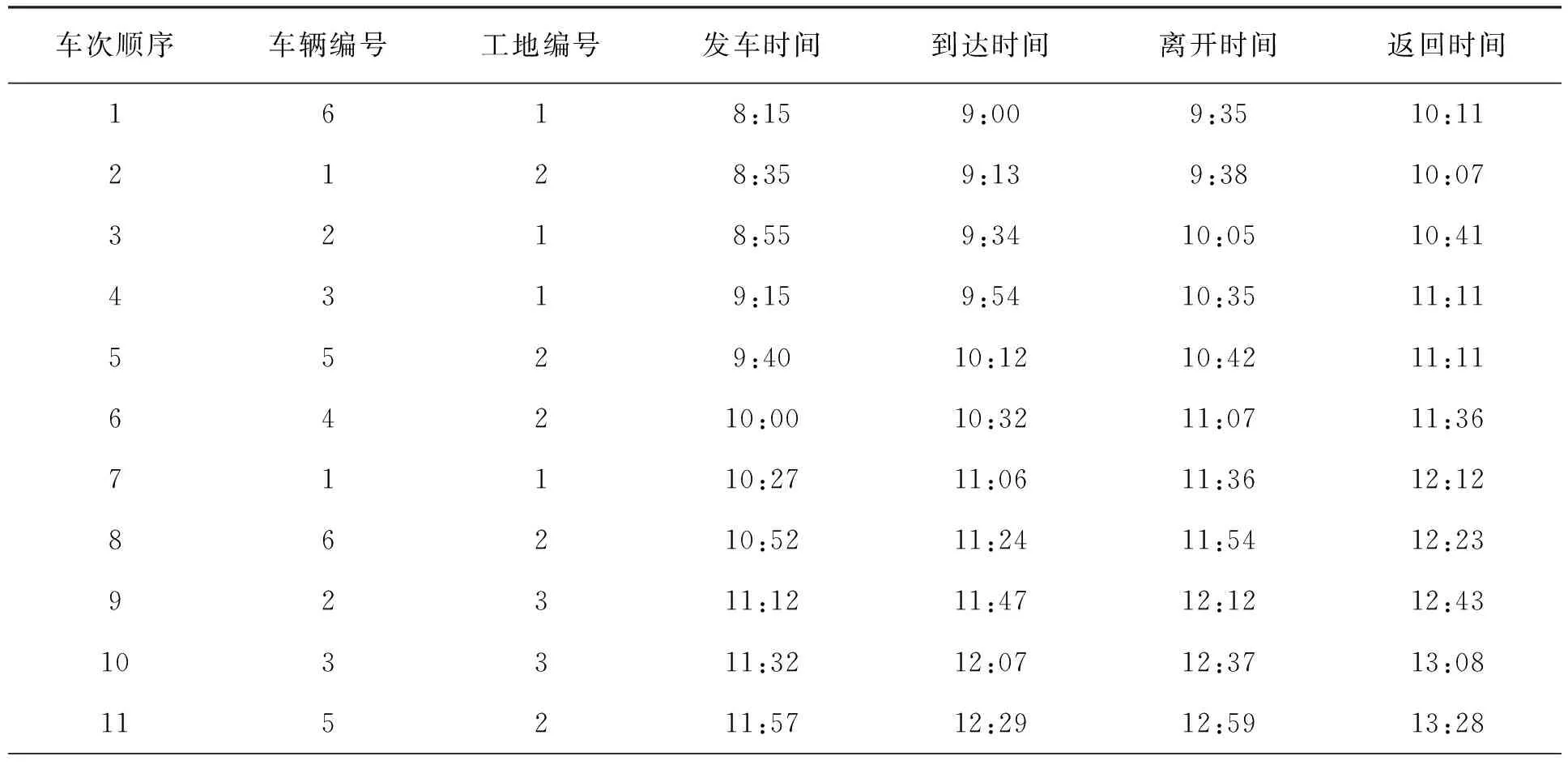
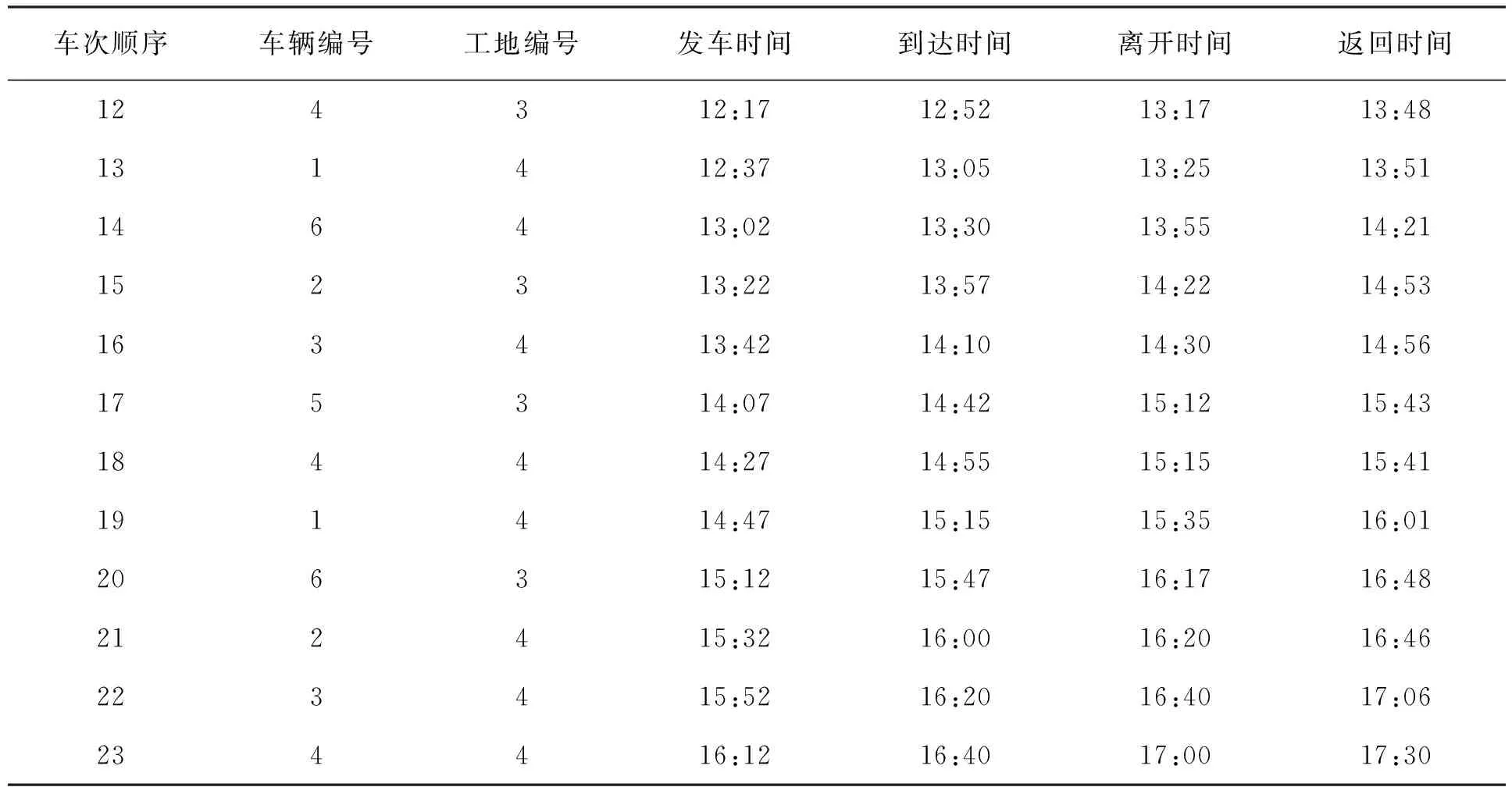
C (24) 式(21)表示车辆首次发车时间应晚于预制厂开始工作的时间FT;式(22)表示预制厂的配送数量满足各工地对构件的需求量;式(23)表示前后两车次发车时间间隔不小于配送车辆的装车时间;式(24)表示预制厂的可配送车辆数小于各工地的总配送车次。 PC构件配送车辆调度优化问题是NP难问题,设计遗传算法对该问题进行求解。遗传算法模仿生物进化过程进行寻优,算法简单高效[11]。首先,对需要解决的问题进行相应的染色体编码,每条染色体便是待解决问题的一个初始解。然后,生成随机种群,根据所研究问题的目标函数设置对应的适应度函数,以此来淘汰种群中的劣势个体。经过选择、交叉、变异等遗传操作来提高种群中染色体的适应度,从中寻找适应度最高的个体[12-13]。 遗传算法具体求解流程如图2所示。 图2 遗传算法求解流程 3.2.1 初始种群编码 将解向量编制成长度为所有工地需求车次之和的染色体。假设有3个施工工地,编号为1、2、3,工地需求车次依次为3、4、3,则染色体长度为10,染色体基因为0-1间的随机数,染色体结构实例如图3所示。 图3 染色体结构实例 将染色体解码后的发车顺序为:2→1→2→3→2→1→1→2→3→3。 3.2.2 适应度计算 由于文中以PC构件配送成本最小为目标,因此,适应度函数取配送总成本的倒数表示 (25) 式中:fi----第i个个体的适应度值; CTi----第i个个体对应的配送总成本,CTi越小,适应度值越大。 3.2.3 选择 分别计算各染色体的适应度值,采用轮盘赌方法选择最优个体。 3.2.4 交叉 染色体采用浮点数编码,因此选择算数交叉,根据两个个体的线性组合生成新个体。 3.2.5 变异 当交叉操作不能产生新个体时,通过变异算子打破局部收敛。 3.2.6 算法终止 算法达到最大迭代次数后,则输出此时的最优解。 选取青岛市某PC构件制造厂作为研究对象,此预制厂主要生产预制梁、柱、叠合板等,且生产数量满足目前签订的4家施工工地的订单需求。 施工工地需求量及时间窗约束见表1。 表1 施工工地需求量及时间窗约束 预制厂目前使用租赁运输车辆进行配送,由于成本与规模的限制,预制厂当天可用于配送的车辆有6辆,根据载重量分为两种车型,在进行配送车辆调度时,可在两种车型中选择并自由匹配,以期达到最低的配送成本。车辆满载时的时速为50 km/h,空载时的时速为55 km/h,柴油当时的市场价格为6.8 元/L。两种车型的相关参数信息分别见表2和表3。 表2 车辆基本信息 表3 不同车型油耗及单位时间燃油成本 配送车辆按照提前规划好的最佳配送路线对施工工地进行配送,配送过程中可能会遇到交通拥堵的状况,该市非高峰期平均拥堵系数为1.08,高峰期(7:00-9:00, 17:00-19:00)平均拥堵系数为1.25。 根据预制厂至施工工地的距离,不同车型的性能参数,以及道路拥堵指数等信息,计算出预制厂至施工工地的运输时间及返回时间,计算结果见表4。 表4 预制厂至施工工地距离及时间信息 4个施工工地对应的单位时间惩罚成本系数β为16元/min,单位时间等待成本系数ω为2.5元/min。 将上述工地需求信息及车辆信息输入到根据模型编写好的代码中,采用Matlab软件进行求解。设置遗传算法的相关参数为:种群规模N=50,交叉概率Pc=0.9,变异概率Pm=0.05,算法达到最大迭代次数100次后终止运行,并输出最优结果。 遗传算法最终计算得出的最低配送总成本为1.065 8万元,未优化前的总成本为1.159 4万元,优化后的方案成本降低8.07%,节省936元。系统运行得到的总成本收敛图如图4所示。 由图4可以看出,此算法具有良好的收敛性能,对模型的求解效果较好。 图4 配送成本收敛图 根据遗传算法求解模型程序命令窗口中输出的结果,对应整理可以得到总配送成本最低时的车辆出车顺序,以及每车次的发车时间,配送车次时间表见表5。 表5 配送车次时间表 续表5 由表5计算结果可以看出,第1车次为编号6的Ⅱ型车8:15出发,发往施工工地1,到达工地的时间刚好为时间窗约束的开始时间9:00,卸车时间花费35 min,10:11返回预制厂;该车辆第二次发车时间为10:52,发往工地2。第2车次为编号1的Ⅰ型车8:35出发,发往施工工地2,到达工地的时间为9:13,卸车时间花费25 min,10:07返回预制厂;该车辆第二次发车时间为10:27,发往工地1,到达工地的时间为11:06。其他情况不再一一列举。 文中从施工工地的视角出发,绘制车辆到达施工工地的时间分布图,如图5所示。 图5 车辆到达时间分布图 通过对比各车次的到达时间与施工工地的时间窗约束可以发现,除工地3的第一车次车辆到达时间略早于工地最早接车时间外,其余车次均在时间窗范围内,说明该调度方案完全满足施工工地对于预制构件送达及时性的要求。 该配送时间表在满足施工单位时间窗要求的前提下,同时考虑了多车型及运输途中的道路交通阻抗情况,派往各工地的发车顺序及时间节点清晰明了。 通过本模型还可输出对应车次的燃油成本、时间等待成本和时间惩罚成本。该模型有利于配送管理人员进行科学的调度管理,避免凭借经验进行车辆安排及一味满足各施工工地需求,而忽略配送过程中额外成本支出的情况,具有良好的适用性。 针对我国装配式建筑PC构件配送成本优化问题,从预制厂的角度出发,综合考虑各施工工地的时间窗约束、道路交通阻抗、多种车型等因素,构建由固定成本、燃油成本、时间等待成本以及时间惩罚成本等四部分组成的预制构件配送总成本优化模型,并设计遗传算法进行求解。通过算例分析,验证了模型和算法的有效性,模型可以有效地反映出PC构件在实际配送过程中的各类成本支出,能够得到配送总成本最低时的配送车辆调度方案及清晰的配送时间表。从而为预制厂的车辆调度工作提供决策依据。3 遗传算法模型
3.1 遗传算法原理
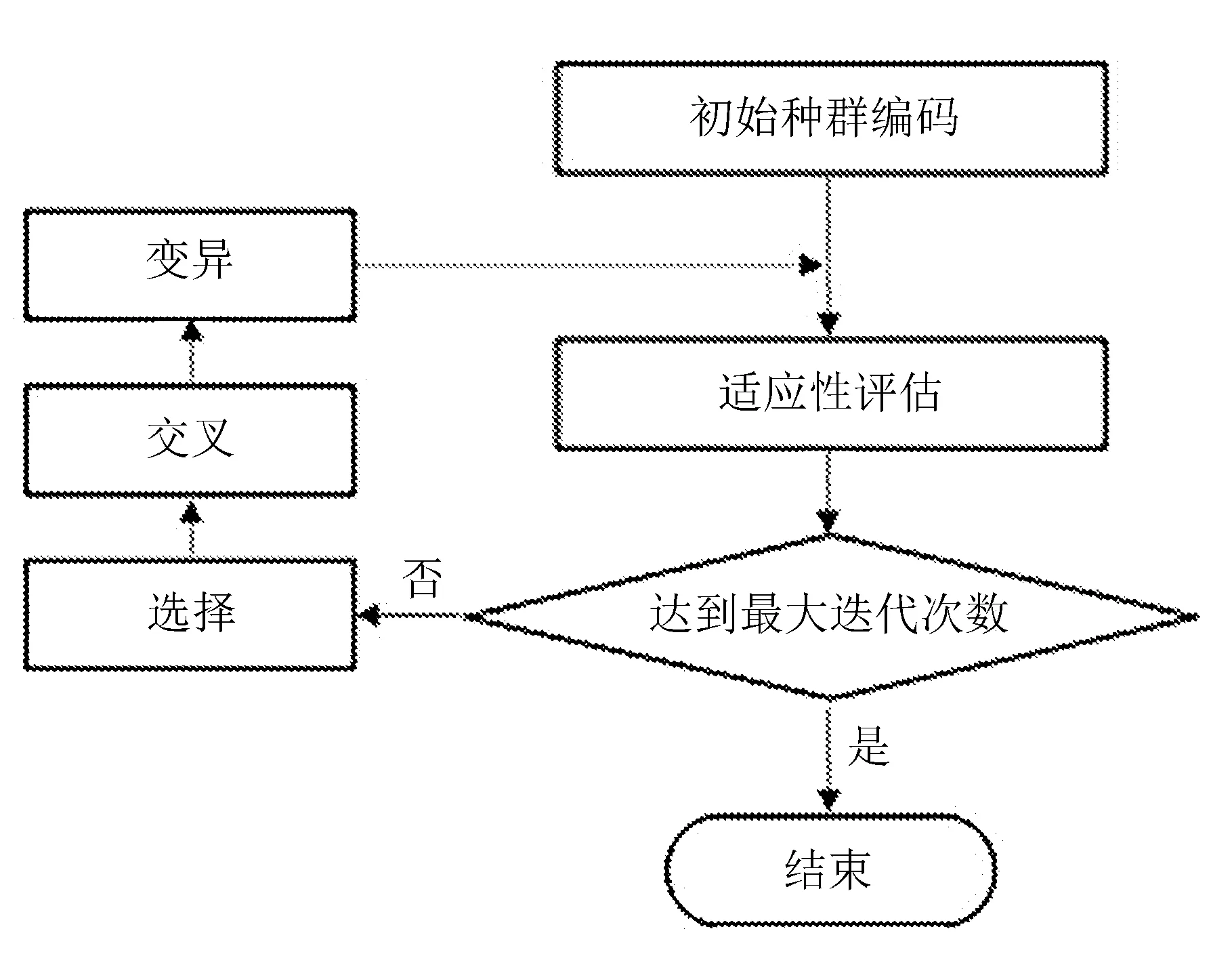
3.2 遗传算法求解步骤

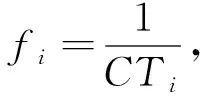
4 算例分析
4.1 算例信息描述



4.2 遗传算法求解

5 结 语
