神经网络多因子选股模型
2022-11-10刘梦尧逄焕利
刘梦尧, 逄焕利
(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)
0 引 言
据统计,截止2020年3月,在上海、深圳、香港、纽约等全球15个交易所上市的中国公司总计7 343家,相比2019年初,新增上市公司382家。总市值达105.71万亿,同比增长超过30%。而投资者也越来越多,量化投资进一步引起了投资者的广泛关注,投资者在七千多家公司中去选择能使自己获得收益的股票,也促使了选股模型的进一步发展。
多因子选股模型是投资者和投资机构应用最广泛的选股模型,这也使得多因子模型不断发展和完善。现今大数据时代,股票和股票因子数据密度越来越大,对其处理需要合理高效的技术。而深度学习高度依赖数据,数据量越大,表现就越好,深度学习中的神经网络算法更能在处理大数据,解决复杂性问题上具有独特优势。
多因子选股的核心思想在于市场影响因素是多重的,并且是动态的,但是总会有一些因子在一定时期内能发挥稳定的作用。量化实践中,由于不同市场参与者或分析师对于市场的动态、因子的理解存在较大差异,因此构建出各种不同的多因子模型。
具有代表性的研究有:张伟楠等[1]使用财务数据构建一个多因子选股模型,在支持向量机分类上进行预测优化,模型利用支持向量机性质提高预测精度,结合技术分析优化了策略的收益,为多因子选股和交易提供了新的研究视角。王伦等[2]为了获取股票市场更高的超额收益,提高股票涨跌预测准确率,将gcForest(深度森林)算法引入了股票投资市场,建立基于gcForest多因子量化投资策略,研究表明,gcForest算法在股市行情平稳和上涨时期都较其他算法有明显的优势。葛橹漠等[3]围绕多量价因子选股模型,通过因子计算、特征处理、单因子分析以及基于XGBoost机器学习的日频滑动窗口模型搭建,计算出XGBoost模型对股票预测的准确度和前100只股票的收益情况,结果表明,基于XGBoost机器学习模型选出的股票组合相对等权重的多因子选股模型有明显的改进。杨妥等[4]提出融合情感分析和SVMLSTM特征提取模型的股指预测方法,以提高股指预测精度,将SVM和LSTM方法相结合建立SVMLSTM模型,提取影响股指波动的情感极性特征、涨跌趋势特征以及股票技术指标特征,进而弥补影响股指波动的存在因素,实现股指预测。
神经网络因其对非线性趋近的函数有很好的处理能力,同时有良好的性能与容错能力,能够弥补传统多因子模型难以处理非线性因子关系的不足,文中利用神经网络非线性、学习、自组织和自适应性等多种特点,有效弥补了传统金融计量模型的短处,取得了可观的超额收益。
1 主流多因子模型概述
1.1 多因子模型的基本概念
在我国公募基金市场中,许多的量化投资基金都是基于多因子模型设立的,在实践中有非常广泛的应用。多因子模型就是对风险和收益关系进行量化表达,通过寻找影响股票涨跌的共性,寻找市场运行规律,利用数据量化的方法,挖掘能够对股票价格变动作出解释和预测的因子,进而构建模型,将其应用到选择股票和管理风险中。
1.2 主流多因子模型
1.2.1 Fama-French三因子模型
在多因子模型被提出之前,CAPM是资产定价的第一范式。然而,自20世纪70年代以来,学者们逐渐发现按照某种风格“打包”的股票能够战胜市场,其中有Basu发现的盈利市值比效应和Banz发现的小市值效应等,但它们并没有形成合力。因此CPAM仍是主流。直到Fama E F等[5]整合了之前被提出的多种异象,指出可以建立一个三因子模型来解释股票回报率。模型认为,一个投资组合(包括单个股票)的超额回报率可由它对三个因子的暴露来解释,这三个因子是:市场资产组合(Rm-Rf)、市值因子(SMB)、账面市值比因子(HML)。
模型公式为
E[Ri]-Rf=βi,MKT(E[RM]-Rf)+
βi,SMBE[RSMB]+
βi,HMLE[RHML],
(1)
式中:E[Ri]----股票i的预期收益率;
Rf----无风险收益率;
E[RM]----市场组合预期收益率;
E[RSMB],E[RHML]----分别为规模因子(SMB)和价值因子(HML)的预期收益率;
βi,MKT,βi,SMB,βi,HML----个股i在相应因子上的暴露。
Fama三因子模型的构建步骤如下:
1)选择已经上市,并且上市时间超过2 a的股票,同时剔除上一年年报中所有者权益为负的股票。
2)将入选股票按每年6月的普通股市值从大到小排序,大于50%分位的归到B组,其余归到S组。按照上年末的账面市值比的大小排序,按30%、70%两个分位,分成三组 L(L,<30%)、M(M,[30%,70%])、H(H,>70%)。将所有既在B组,又在L组的股票分到BL组中,以此类推,将所有股票都分别分到 BL、BM、BH、SL、SM、SH这6个组中,见表1。

表1 股票市值分组表
3)将股票在每年6月份,分别按市值、账面市值比大小分成5组,交叉取交集,得到25组股票组合,每个组合计算市值加权月收益率序列。重复以上过程,得到三因子收益率,以及25组组合的月收益率,将这25组组合的收益率逐组与三因子收益率进行时间序列回归,并检验其结果。
实验证明,三因子模型可以很好地解释股票的平均收益,而且回归分析的截距接近于0(Alpha接近于0),这意味着市场因子、规模因子和账面市值比因子三者一起可以很好地解释股票市场中的收益。此模型被提出后就逐步取代了CAPM成为资产定价的第一范式。
1.2.2 Carhart 四因子模型
随着市场交易实践和研究的不断深入,研究者又发现市场中的动量现象无法用三因子模型解释。1997年,卡哈特(Carhart M M)[6]认为研究股票收益应在Fama和French的三因子模型基础上加入动量效应,构建四因子模型,模型公式为
E[Ri]-Rf=βi,MKT(E[RM]-Rf)+
βi,SMBE[RSMB]+
βi,HMLE[RHML]+
βi,MOME[RMOM],
(2)
式中:E[RMOM]----动量因子的收益率;
βi,MOM----个股i在动量因子上的暴露。
Carhart 四因子模型在Fama三因子模型的基础上,每月末将所有股票按t-12到t-1这11个月的总收益排序,并通过做多排名前30%,同时做空排名后30%的股票构建动量因子。在计算因子收益率时,多空两头内的股票均采用等权重配置。
实验证明,考虑动量因子之后,回归精确度有所提高。Carhart四因子模型弥补了三因子模型对市场“趋势效应”解释不足的问题,更全面地评价基金业绩,并且更有效地衡量基金的超额收益能力具有一定的学术地位和实践意义,使投资者能够简明直观地看到目标基金的收益和风险来源。
1.2.3 Fama-French五因子模型
2015年,Fama E F等[7]在Fama-French三因子模型的基础上,添加了盈利和投资两个因子,提出了新的五因子模型,模型公式为
E[Ri]-Rf=βi,MKT(E[RM]-Rf)+
βi,SMBE[RSMB]+
βi,HMLE[RHML]+
βi,RMWE[RRMW]+
βi,CMAE[RCMA],
(3)
式中:E[RRMW],E[RCMA]----分别为盈利因子和投资因子的预期收益率;
βi,RMW,βi,CMA----分别为个股i在这两个因子上的暴露。
Fama五因子模型的构建与Fama三因子模型类似:
1)完成股票筛选后,选取因子截面数据。
2)市值规模的分组点为中位数,前50%为小规模组(S),后50%为大规模组(B),账面市值比的分组点都为第30个和第70个百分位数,前30%为低账面市值比组(L),中间40%为中账面市值比组(N),后30%为高账面市值比组(H),将市值和账面市值比两个指标交叉, 可把全体股票分成SH、SN、SL、BH、BN、BL这6个组合。重复上述步骤, 可把全体股票分成 SR、SN、SW、BR、BN、BW、SC、SN、SA、BC、BN、BA这12个组合, 其中,营运利润率前30%为盈利疲软组(W),中间40%为盈利中等组(N),后30%为盈利稳健组(R);投资前30%为投资保守组(C),中间40%为投资中等组(N),后30%为投资激进组(A),接下来计算上述各组合每一期的市值加权平均收益率。
3)分25组回归的时候,计算组合收益率采用流通市值加权平均法计算的组合收益率。
结果显示该模型增加了企业的盈利能力因子与投资风格因子,提出了五因子模型,并通过实证检验发现,在美国股票市场上五因子模型比三因子模型对股票收益率有更好的解释能力。这两个因子在理论上同样有对有价证券收益率的显著影响。
Fama-French五因子模型以其简洁优美的表述,以及精炼的概括性受到了广泛应用,但其对有价证券的研究也仅限于企业的基本面因素,并未考虑其他因素对有价证券收益的影响。
2 基于神经网络的多因子模型构建
2.1 数据准备工作
2.1.1 数据的获取
量化投资研究需要大量高质量的数据,因此,一个可靠的数据来源十分重要。目前,国内各大量化交易平台均提供了较为丰富的数据,投资者在平台进行研究时可以免费调用平台数据,文中使用聚宽量化投资中的数据来进行研究。
2.1.2 数据的预处理
因子数据是多因子选股模型的数据基础,只有高质量的因子数据才能保证研究的准确性和有效性,所以在模型构建前需要对数据进行预处理,以避免金融数据行业偏向等问题对实证研究结果的客观性产生影响。
2.1.3 中性化处理
对因子进行中性化是要消除行业、市值因素对因子测试结果的影响,如果不剔除行业和市值的影响,可能会导致选出来的股票集中在某个行业和某种市值范围内,进而导致不能有效地分散风险。文中采用因子值为因变量,行业因子和市值因子分别为自变量构建线性回归方程

(4)
构建上述回归方程后,取残差项εi作为新的因子值。同理,在进行完行业中性化后,再进行市值中性化

(5)
式中:λi----残差项,即经过行业中性化、市值中性化的新的因子值。
2.2 单因子测试
每个因子都不可能保证持续的有效性,因此需要对因子进行测试,表现好的因子保留,不好的剔除,文中将使用IC法、分层回溯法两种方法对因子进行测试。
2.2.1 IC法
IC值是因子在t期的暴露度与t+1期的资产收益率之间的相关系数,即

(6)
式中:ri----资产在t+1期的收益率;
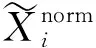
IC法用来检验因子对于收益预测能力的强弱。
正向因子的IC值序列如图1所示。
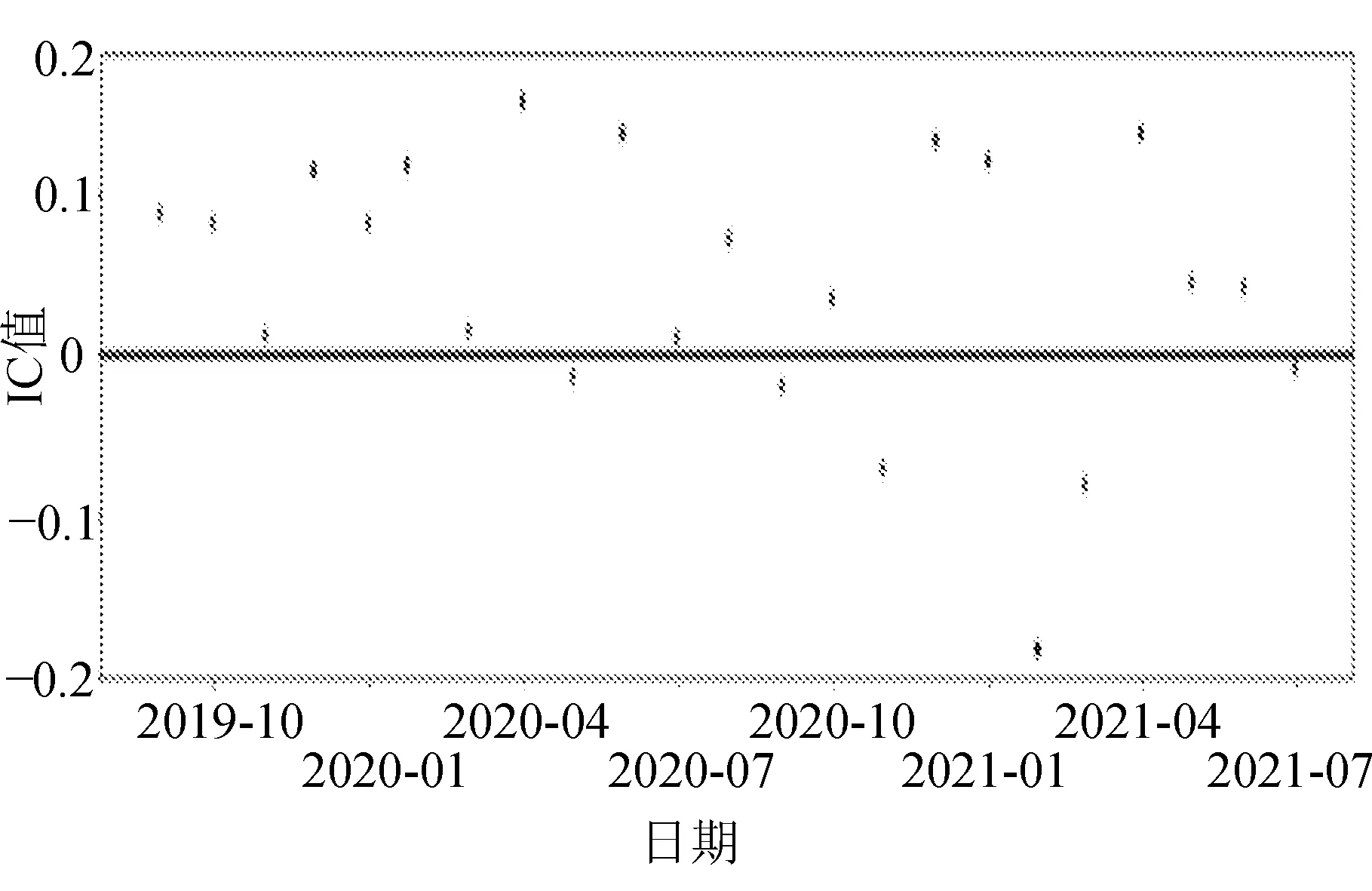
图1 total_asset_growth_rate因子IC值序列
图中上方深色点多余下方深色点,代表该因子为正向因子,表示该因子与收益率是正相关,深色点越多,代表该因子的收益预测能力更强。
反向因子的IC值序列如图2所示。
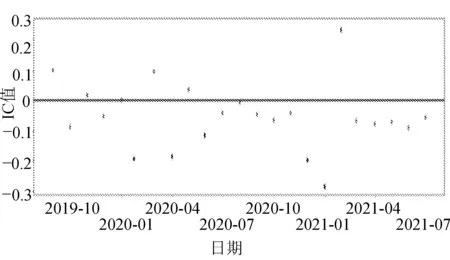
图2 fifty_two_week_close_rank因子IC值序列
图中下方深色点多余上方深色点,代表该因子为反向因子,表示该因子与收益率呈负相关,同样深色点越多,代表该因子的预测能力更强。
2.2.2 分层回溯法
分层回溯法可以观察因子收益率的单调性。具体方法在t期,根据因子值对股票(资产)进行排序,将结果五等分,用五等分的结果构建投资组合,计算这五个投资组合在t+1期的收益率;然后在t+1期再次根据因子值进行股票的排序,将结果五等分,之后根据五等分的结果构建投资组合,计算五个投资组合在t+2期的收益率,以此类推。观察五等分之后的收益率情况,如果五个投资组合的收益率递减或者递增的规律性越强,则该因子的效果越好。
total_profit_growth_rate因子分组组合表现如图3所示。
图中五组投资组合收益率的递增效果明显,表示该因子的分组能力突出,且该因子与收益率呈正相关。
经过上述因子筛选过程后,选取了选股能力和分组能力相对较好的因子18个,见表2。

图3 total_profit_growth_rate因子分组组合表现

表2 因子表
2.3 基于神经网络的多因子模型
神经网络是通过不同的层次架构将神经元进行连接运算,从而完成各类复杂的分类与拟合任务。神经网络具有普适性、自适应、泛化等优势,可以通过中间层的设计逼近任意的非线性函数,并且通过对带有标签的实例数据提取相应规则,可以很好地对数据中噪声数据进行处理,从而较好地应对生活中的复杂问题。
神经网络的网络结构如图4所示。
图中,输入向量为
X=(x1,x2,x3,…,xn)T,
即为股票的因子数据。
隐含层向量为
Z= (z1,z2,z3,…,zn)T。
输出层输出向量为
Y= (y1,y2,y3,…,yn)T,
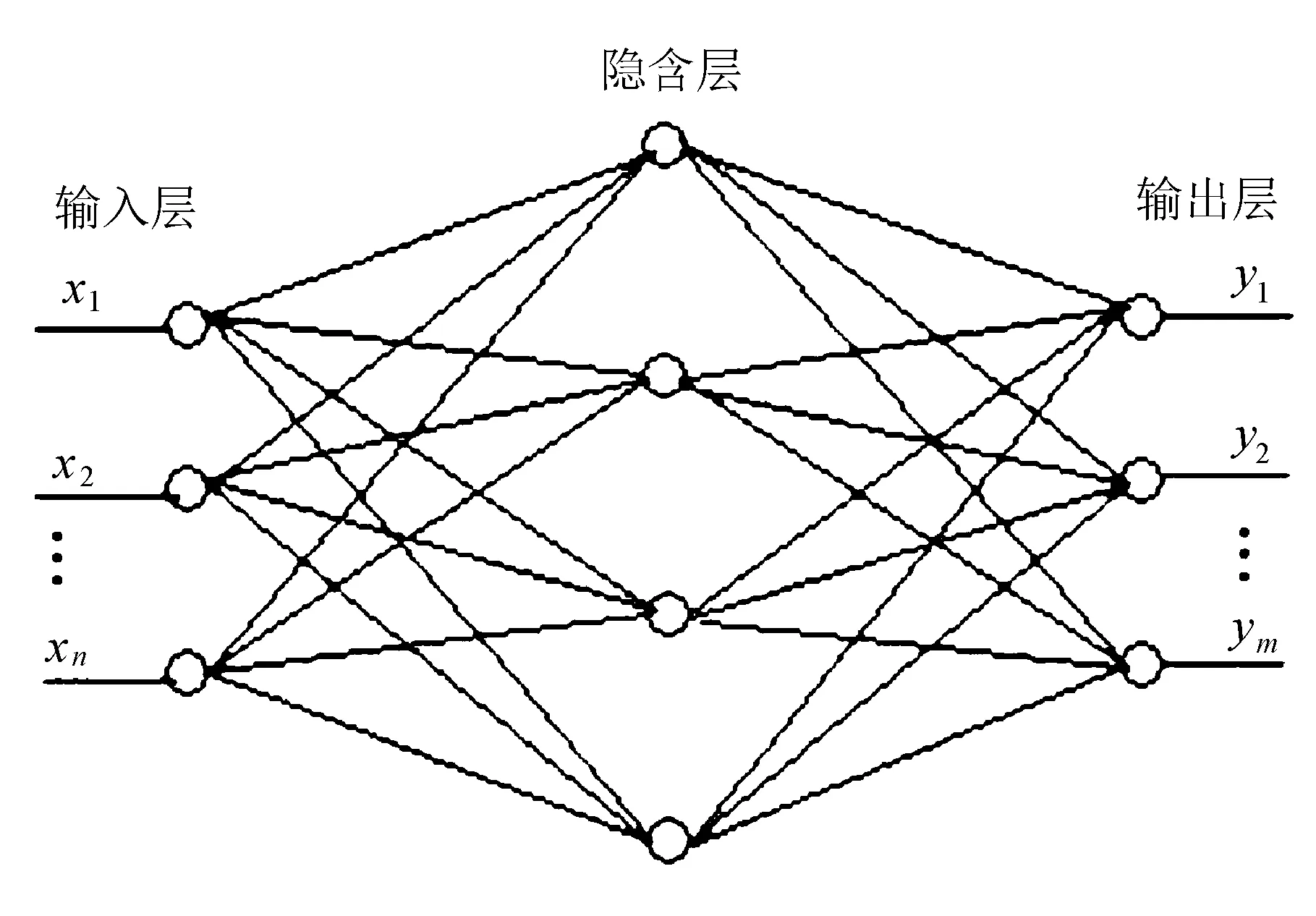
图4 神经网络结构
即对股票的预测结果(上涨或下降)。将输入层与隐含层之间的链接权重矩阵定为W1,隐含层到输出层之间的权重矩阵定为W2。
根据神经网络预测结果,每日买入上涨概率前5%的股票,见表3。
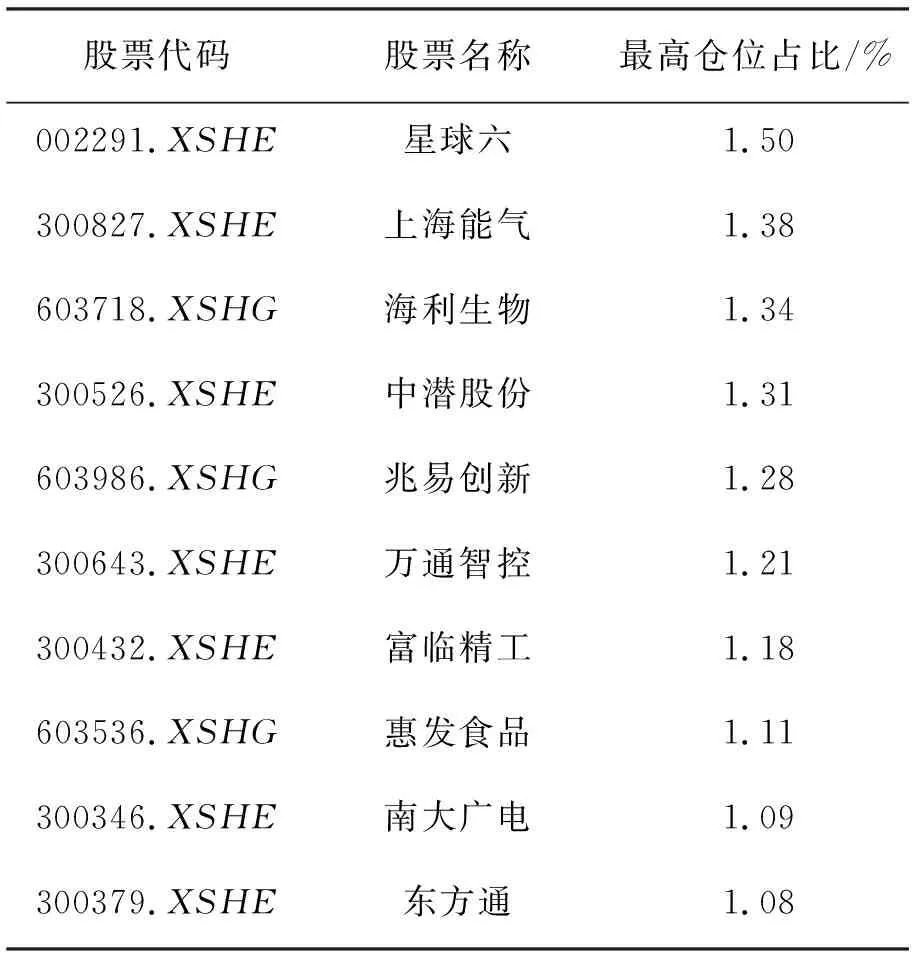
表3 前10大持仓股票
2.4 回测结果分析
根据上述基于神经网络的多因子模型选出的股票,得到回测结果见表4,
由表4可知,在回测期间,也就是2019年8月至2021年8月,沪深300指数的累计收益率为60.82%。

表4 策略收益表现
相较于基准收益率,基于神经网络的多因子选股模型构建的投资组合收益曲线如图5所示。
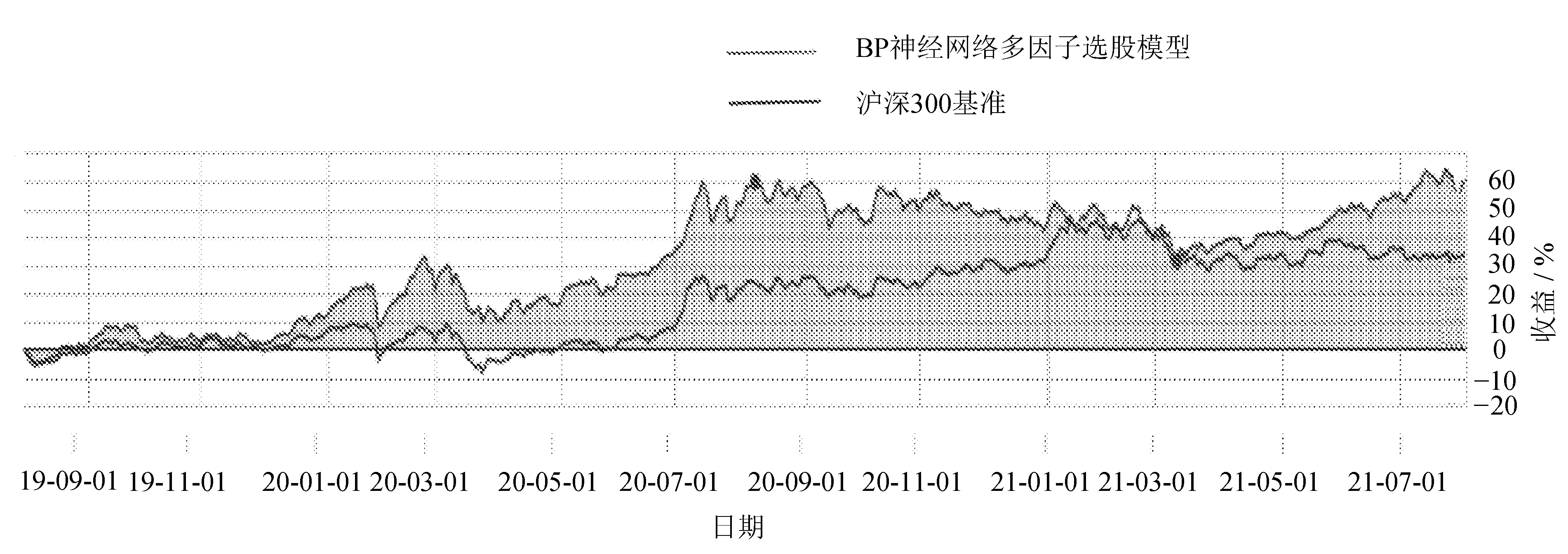
图5 策略收益图
从图5可以看出,文中构建的选股模型获得了60.82%的累计收益率,相较于基准收益率,获得了28.21%的超额收益率。该策略的阿尔发值为0.158,表示该策略的超额回报率为0.158;贝塔值为0.942,表示文中策略对大盘变化的敏感性为0.942;夏普比率为1.004,也就是说,在承担相对于基准指数的总风险获得的超额收益为1.004,即该策略的回报率大于其风险;索提诺比率为0.866,即每承担一单位的下行风险,该策略将会获得0.866的超额回报率;信息比率为1.224,说明该策略在承担主动风险所获得的超额收益为1.224 7;最大回撤为17.30%,表示投资者在策略面对风险时的承受能力较好。该投资组合相较于基准组合的胜率为62.6%。
3 结 语
利用IC法、分层回溯法选取了18个有效因子,使用IC_IR加权法对因子进行加权,并构建了基于神经网络的量化多因子选股模型。文中在选取有效因子时,除了考虑部分基本面因子,还考虑了动量因子和技术因子,使策略面对风险和市场波动时具有一定的调整能力。实证分析,文中构建的策略获得了28.21%的超额收益,且具有一定的抵抗风险和市场波动的能力,由此可知,根据神经网络预测出的股票组成的投资组合可以获得更高的收益,神经网络在量化选股模型上值得进一步研究。
