基于关系矩阵的传递闭包求解方法＊

郭丽君

(兰州博文科技学院电信工程学院，甘肃 兰州 730101)

0 引言

二元关系是离散数学集合论中的重要概念，在计算机学科的相关专业中应用极为广泛，如数据库、数据结构、语法分析理论等，很多相关理论和研究判定方法都是建立在关系传递闭包运算的基础上[2-6]，因此关系的传递闭包运算也成了很多学者争相研究的对象[7-13]，已有理论虽然已经得到了一些很好的结果，但方法仍略显繁琐和复杂，使得学生在理解的过程中存在困难。通过利用关系的关系矩阵，不用对关系中的有序偶做过多的判断和对比，也不必对元素进行筛选和删除，仅使用矩阵的简单运算，给出了传递闭包运算较为简单的方法，使得学生在学习的过程中易理解、易接受，且在此基础上进一步通过计算机编程的方法求解较庞大的关系的传递闭包有了理论依据。

1 基本定义和定理

定义1设R 是集合X 上的关系，若R ⊆R＇且R＇是传递的，若另有R ⊆R＇＇且R＇＇是传递的，则必有R＇ ⊆R＇＇，此时称R＇是R的传递闭包，记为t(R)=R。

定义2设定义在集合X={a1,a2,…,an}上的关系R，定义其关系矩阵为A=(aij)n，其中

定义3设R是集合X上的关系，定义Rn=R◦R◦…◦R（符号＂◦＂表示关系R的复合运算）。

定理1[1]设R是集合X上的关系，则R的传递闭包

定理2设R 是有限集合X 上的关系，且 ||X=n,则R的传递闭包t(R)=

2 主要结论

定理3设R 是集合X 上的关系，且 |X |=n，A为关系R的关系矩阵，必存在正整数k＜n，使得A(k)=O（零矩阵）或A(k+1)=A(i),i=1,2,…,k，则关系R 的传递闭包对应的关系矩阵为

即A＇对应的关系R＇=t(R)。

另一方面，令Xi={ai}，分以下三种情况讨论。

⑴当Xi≠Xj，且有(ai,aj),(aj,ai)∉R 时，由于Rn=R◦R◦…◦R，在关系的复合过程中，元素是递减的状态，必存在正整数k＜n，使得Rk=∅，即A(k)=O（O为零矩阵）。

⑵ 当Xi≠Xj，且 有(ai,aj),(aj,ai)∈R 时，由 于(ai,aj)◦(aj,ai)=(ai,ai)，而(ai,ai)◦(ai,aj)=(ai,aj)，因 此必存在正整数k＜n，使得A(k+1)=A(i),i=1,2,…,k。

⑶ 当Xi=Xj时，必存在正整数k＜n，使得Rk={(ai,ai)}，Rk+1=R，即A(k+1)=A。

因此t(R)对应的关系矩阵为

A＇=A(+)A(2)(+)…(+)A(k),k＜n

证明完毕。

例1设集合X={a,b,c,d}，定义集合X 上的关系R={(a,b),(a,c),(b,c),(b,d)}，通过关系矩阵求R 的传递闭包。

解：根据公式⑴先写出关系R 的关系矩阵A，依次求出A(2),A(3)：

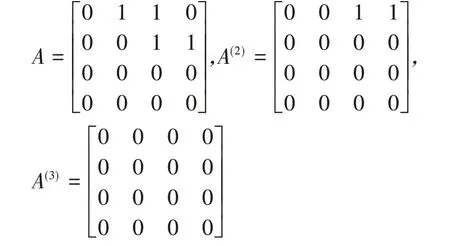
由于A(3)=O，因此计算可以终止，由公式⑵可得

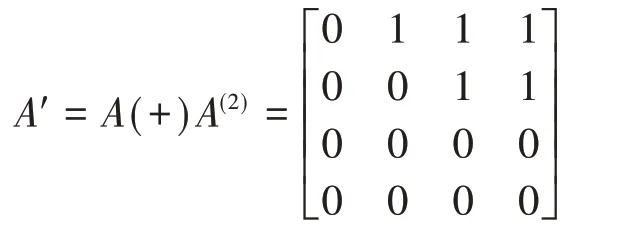
由此得到关系矩阵A＇对应的关系R＇={(a,b),(a,c),(a,d),(b,c),(b,d)}即为关系R的传递闭包。

例2设集合X={a,b,c,d}，定义集合X 上的关系R={(a,b),(c,b),(b,c),(c,d)}，通过关系矩阵求R 的传递闭包。

解：根据公式⑴先写出关系R 的关系矩阵A，依次求出A(2),A(3)：

显然A(4)=A(2)，因此计算可以终止，由公式⑵可得

由此得到关系矩阵A＇对应的关系R'={(a,b),(a,c),(a,d),(b,b),(b,c),(b,d),(c,b),(c,c),(c,d)}即为关系R的传递闭包。

例3设集合X={a,b,c,d}，定义集合X 上的关系R={(a,b),(c,a),(b,c)}，通过关系矩阵求R的传递闭包.解：根据公式⑴先写出关系R 的关系矩阵A，依次求出A(2),A(3)：

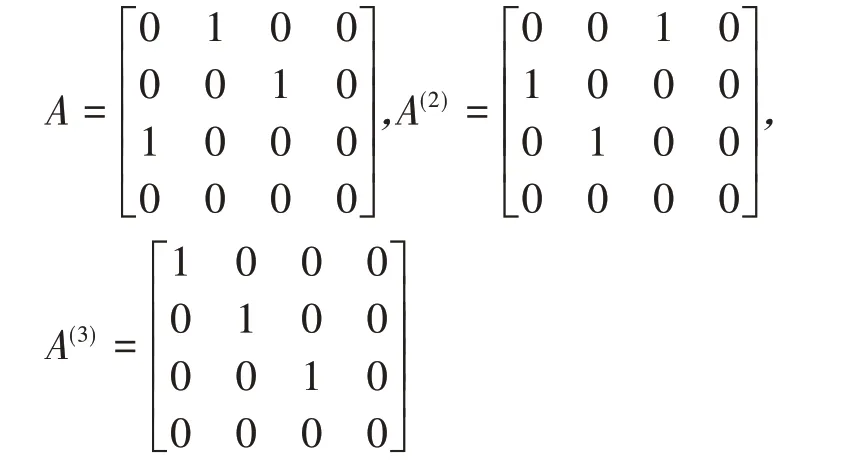
此时A(4)=A，因此计算终止，由公式⑵可得

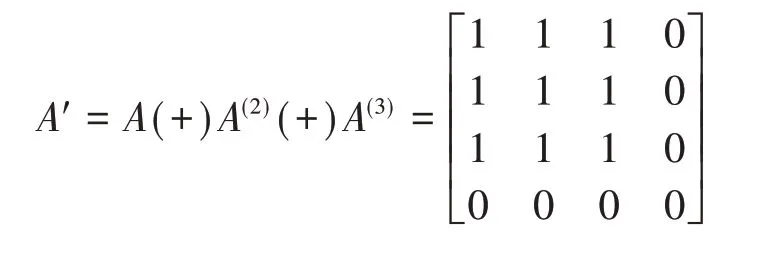
矩阵A＇对应的关系R'={(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)}即为关系R的传递闭包。

3 算法分析

通过写出关系R 的关系矩阵，利用矩阵运算的方法得到关系R 的传递闭包所对应的关系矩阵，进而写出传递闭包的过程，这显然比现有的传递闭包运算方法要简单的多，更易操作。同时，利用计算机编程去解决更复杂的关系也得以实现。另一方面，在计算一个关系的传递闭包时，还要考虑关系自身的性质，若关系R 自身具备传递性，则t(R)=R，利用该方法求关系的传递闭包时，不用验证关系R 的性质，对于满足传递性的关系来说该方法仍然适用。

具体给出算法如下：

⑴写出关系R 的关系矩阵A（A中仅有0,1 两个元素）；

⑵ 使用布尔和与布尔乘的方法计算继续计算A(k),k=2,3,…,n（A(k)中仅有0,1两个元素）；

⑶当A(k)=O或A(k+1)=A(i)，i=1,2,3,…,k时结束；

⑷计算A＇=A(+)A(2)(+)…(+)A(k)；

⑸输出A＇即为关系t(R)的关系矩阵，计算结束。

4 结束语

通过使用关系矩阵求解关系的传递闭包，在主要结论定理3 的证明中分三种情况对关系进行了讨论，通过三个对应情况下的例题进行了佐证。与现有的方法相比，该方法在求解过程中不用对关系中的有序偶做过多的判断和对比，也不必对元素进行筛选或删除，求解方法简单易懂，可对学习关系闭包运算的师生带来一定启发，同时为进一步利用计算机编程来求解关系的传递闭包提供了理论依据。