Quantum Remote State Preparation Based on Quantum Network Coding

Zhen-Zhen Li,Zi-Chen Li,Yi-Ru Sun,＊,Haseeb Ahmad,Gang Xu and Xiu-Bo Chen

1School of Information Engineering,Beijing Institute of Graphic Communication,Beijing,102600,China

2School of Computer Science and Information Engineering,Zhejiang Gongshang University,Hangzhou,310018,China

3Information Security Center,State key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing,100876,China

4Department of Computer Science,National Textile University,Faisalabad,37610,Pakistan

5School of Information Science and Technology,North China University of Technology,Beijing,100144,China

6Advanced Cryptography and System Security Key Laboratory of Sichuan Province,China

Abstract:As an innovative theory and technology,quantum network coding has become the research hotspot in quantum network communications.In this paper,a quantum remote state preparation scheme based on quantum network coding is proposed.Comparing with the general quantum remote state preparation schemes,our proposed scheme brings an arbitrary unknown quantum state finally prepared remotely through the quantum network,by designing the appropriate encoding and decoding steps for quantum network coding.What is worth mentioning,from the network model,this scheme is built on the quantum k-pair network which is the expansion of the typical bottleneck network—butterfly network.Accordingly,it can be treated as an efficient quantum network preparation scheme due to the characteristics of network coding,and it also makes the proposed scheme more applicable to the large-scale quantum networks.In addition,the fact of an arbitrary unknown quantum state remotely prepared means that the senders do not need to know the desired quantum state.Thus,the security of the proposed scheme is higher.Moreover,this scheme can always achieve the success probability of 1 and 1-max flow of value k.Thus,the communication efficiency of the proposed scheme is higher.Therefore,the proposed scheme turns out to be practicable,secure and efficient,which helps to effectively enrich the theory of quantum remote state preparation.

Keywords:Quantum remote state preparation;quantum network coding;quantum k-pair network

1 Introduction

In 2000,quantum remote state preparation (RSP) was first proposed by Lo[1].RSP enables the senders to prepare known states for remote receivers with the assistance of entangled resources[2,3]and classical communications[4,5].With so many years of development,RSP has already made significant advances in theories[6-8]and applications[9-11].In these researches,respect to the different target state,such as Bell state[12],GHZ state[13],W state[14],cluster state[15]and so on,various kinds of RSP schemes have been proposed.In addition,respect to the different implementation techniques,such as deterministic RSP[16],joint RSP[17]and controlled RSP[18],several schemes have also been proposed.

However,with the development of quantum communication and the requirement for multi-user’s quantum communication,point-to-point communication mode will necessarily toward to the direction of network communication.Thus,the research of RSP over the quantum network have become a meaningful task.In quantum network communications,as a breakthrough technology,quantum network coding(QNC)can effectively improve the quantum communication efficiency and quantum network throughput as compared to the traditional technology of routing.Since the first QNC scheme proposed by Hayashi et al.[19]in 2006,a series of QNC schemes have been put forward in theories[20-23]and applications[24-26]over the past decade.By QNC,the intermediate nodes are allowed to encode the received information and ultimately the destination nodes can recover the original unknown quantum state by decoding.Therefore,it is reasonable to believe that if combining RSP and QNC,the problem of quantum state preparation over quantum networks can be solved effectively.

In this paper,a novel RSP scheme based on QNC is proposed.This scheme is assisted by the resource of prior entanglement and classical communication,and the specified encoding or decoding operations are performed at the corresponding nodes.In terms of the quantum state,an arbitrary unknown quantum state possessed by the source nodes are finally prepared at the sink nodes;in terms of the success probability,this scheme can always achieve the success probability of 1;in terms of the network model,the quantum k-pair network as an expansion of the typical bottleneck network—butterfly network[27-29]in QNC is constructed to propose the scheme.Thus,the proposed scheme can effectively improve the communication efficiency and is more applicable to the scenarios of largescale quantum networks,which can enrich the theory of quantum remote state preparation over quantum network.

The remainder of this paper is organized as follows.In Section 2,preliminaries including notations,quantum k-pair network,quantum operators and quantum measurements are presented.In Section 3,the specific RSP scheme based on QNC is proposed.In Section 4,the performance analyses including correctness,security,practicability and achievable rate region are discussed.At last,some concluding remarks are given in Section 5.

2 Preliminaries

2.1 Notations

The following notations will be used throughout this paper:

⊕:The addition module d;⊗:The tensor product of vector space.

Cd:The d-dimension complex field;Zd:The integer ring with respect to addition ⊕module d.

σx:The Pauli operator over 2-dimension space;X/R:The Pauli operator over d-dimension space.

2.2 Quantum K-Pair Network

Let us consider a directed acyclic graph(DAG)G=(V,E),where V is the set of nodes and E is the set of edges that connect pairs of nodes in V.K pairs of nodes(s1,t1),(s2,t2),...,(sk,tk)constitute a subset of V.Next,a directed acyclic network(DAN)N is deemed a quantum network if it comprises a DAG G and the edge quantum capacity function c :E →Z+.The quantum k-pair network N explored herein is shown in Fig.1.

Figure 1:Quantum k-pair network N

In this figure,the solid lines represent the quantum physical channels and the arrows indicate the transmission direction of the quantum information.Let H=Cddenote a Hilbert space.According to the task of the quantum RSP and QNC,one needs to make a quantum state|Ψ〉S1,...,Sk∈H⊗ksupported on the source nodes s1,...,sk(in this order)remotely prepared at the sink nodes t1,...,tk(in this order)through N,under the condition that c(e) ≡1,e ∈E,i.e.,each edge of N can transmit no more than one qudit state over H.For i ∈{1,2,...,k},each quantum register Siis possessed by the source node si,while the quantum register Tiis possessed by the sink node ti.A RSP scheme based on QNC over the quantum k-pair network refers to the corresponding protocol,which contains certain quantum operations for all nodes in V that enable the above preparation to be accomplished successfully.

2.3 Quantum Operators

2.4 Quantum Measurements

3 A Quantum Remote Preparation Scheme Based on Quantum Network Coding

3.1 Protocol Specification

3.2 Example:The Butterfly Network Over H=C2

For the quantum k-pair network N illustrated in Fig.1,when k=2,the network becomes the typical bottleneck network—butterfly network as shown as Fig.2.This subsection describes the techniques developed in the previous descriptions using the example of the butterfly network over Hilbert space H=C2.

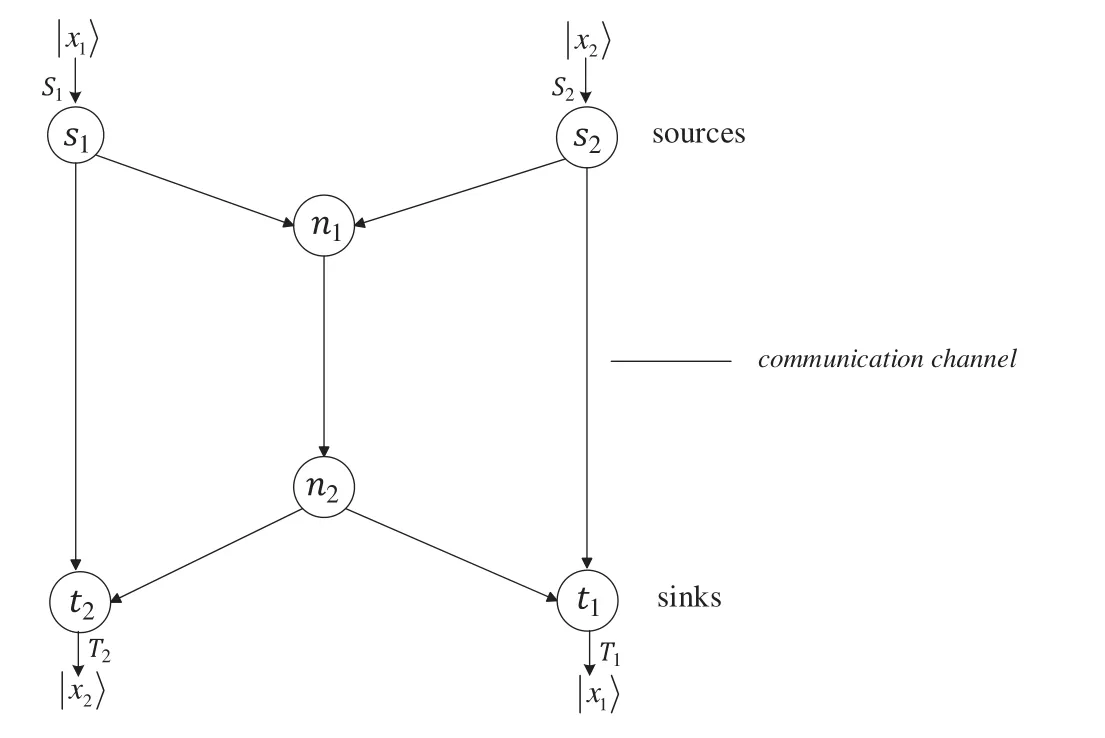
Figure 2:Quantum butterfly network

Hereafter,we proceed to the specific steps of the RSP scheme based on QNC.For step 1-step 4,it can be considered as the encoding process and the object is to make the particles in the quantum registers mutually entangled.The corresponding schematic diagram of quantum circuit can be shown in Fig.3.

Figure 3:Schematic diagram of quantum circuit for steps 1-4

According to the specific calculations,after Step 1-4,the quantum states of the of the whole system becomes

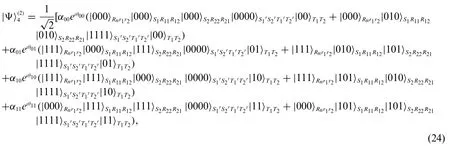
Then,For Step 5-Step 9,it can be considered as the decoding process and the object is to remove the particles in the unnecessary quantum registers.The corresponding schematic diagram of quantum circuit can be shown in Fig.4.

Figure 4:Schematic diagram of quantum circuit for steps 5-9

According to the specific calculations,the quantum states of Step 5-9 are detailed as follows:

4 Scheme Analysis

4.1 Correctness

The correctness of the proposed RSP scheme based on QNC can be verified by the specific steps.From Section 2,in the Step 1-4,the particles at every network node are entangled to the whole quantum system by applying relevant quantum encoding operations.The resulting quantum state after the entanglement of each time is presented specifically.In the Step 5-9,by applying relevant quantum measurements called decoding operations,all the unnecessary particles are disentangled from the whole quantum system and leave alone the certain particles on the sink nodes.The resulting quantum state after the disentanglement of each time is also presented specifically.Thus,after all the encoding and decoding steps,the final quantum state at the sink nodes formedIs exactly equal to the initial source state |Ψ〉S=,at the source nodes.Therefore,according to all the calculating procedure and numerical results,the correctness of the proposed RSP scheme is verified.What is worth mentioning,in this proposed scheme,the probability of successful preparation can always reach 1.

4.2 Security

In the existing RSP schemes[12-18],the quantum state desired to be prepared remotely is known for the senders,i.e.,the amplitude coefficient and the phase coefficient is known.However,in many actual scenarios,if the senders are not honest,then the final quantum state prepared remotely is likely to be mistaken.In this paper,the proposed RSP scheme is based on QNC,which means that the senders do not need to know the desired quantum state and finally it can be prepared remotely.Therefore,the security of the proposed RSP scheme here is higher.

4.3 Practicability

In the existing RSP schemes[12-18],the point-to-point communication mode is used.With the development of quantum communication,quantum network communication containing more users has become a necessity.In this paper,the proposed RSP scheme based on QNC is established over the quantum k-pair network which is the typical bottleneck network model.Using this scheme,the quantum network congestion can be solved effectively and the communication efficiency is higher.Thus,the proposed scheme can be more applicable to the scenarios of large-scale quantum networks.

4.4 Achievable Rate Region

5 Conclusions

In this paper,we propose a novel RSP scheme based on QNC over the quantum k-pair network.In terms of the quantum state,an arbitrary unknown quantum state is finally prepared at the sink nodes;in terms of the success probability,this scheme can always achieve the success probability of 1;in terms of the network model,the quantum k-pair network is the expansion of the typical bottleneck network—butterfly network.Thus,the proposed scheme can effectively improve the security and communication efficiency,and is more applicable to the large-scale quantum networks,which can enrich the theory of quantum remote state preparation.

Acknowledgement:We express our heartfelt thanks to the Beijing Institute of Graphic Communication for funding this study,as well as to the State Key Laboratory of Networking and Switching Technology for offering technical support.

Funding Statement:This work is supported by the National Natural Science Foundation of China(Grant Nos.61370188,62176273,61962009),the Scientific Research Common Program of Beijing Municipal Commission of Education(KM202010015009,KM202110015004),Initial Funding for the Doctoral Program of BIGC(27170121001/009),the Open Foundation of State key Laboratory of Networking and Switching Technology(Beijing University of Posts and Telecommunications)(SKLNST-2021-1-16),the Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province (Grant No.SKLACSS-202101) ,the Fundamental Research Funds for Beijing Municipal Commission of Education,Beijing Urban Governance Research Base of North China University of Technology,and the Natural Science Foundation of Inner Mongolia(2021MS06006).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.