误差系数对变分同化的质量影响研究*
2022-11-09蒋金利诸雪征韩朝帅李广峰
蒋金利 诸雪征 顾 进 韩朝帅,2 马 岩,3 李广峰
(1.陆军防化学院 北京 102205)(2.军事科学院防化研究院 北京 102205)(3.武警四川总队机动第二支队 康定 626000)
1 引言
数据同化算法是一种最初来源于数值天气预报,为其提供初始场的数据处理技术,现已广泛应用于大气海洋领域。在积分描写动力系统演变过程的数学模式的同时,不断吸收观测资料,给出系统状况的整体估计,且观测资料仅仅通过少量的观测站便可获取,大大降低经济成本,并有效提高了数值天气预报的准确度与可靠性。
国外早在1922年,Richadson就首次将同化的思想用于数值天气预报的主观分析中[1]。当时他将观测数据以手工的方式插值到网格点,以此作为预报的初始场,因为方式过于简单,未做其他误差处理,导致最后预报失败。我国在该领域最早的研究是1958年顾震潮学者提出数值天气预报不是简单的初值问题[2]。20世纪60年代我国著名气象学家丑纪范创造性地提出将变分法和泛函分析引入数值天气预报领域,该理论比国外同行的研究早了近十年。
目前主流的数据同化算法主要分为两类(按照算法与模型之间的关联机制分类):
1)以卡尔曼滤波、集合卡尔曼滤波等算法为代表的顺序数据同化算法。
2)以三维变分、四维变分等算法为代表的连续数据同化算法。
其中,自从20世纪90年代以来,随着计算机性能的大幅度提升,变分同化算法在实际应用中得到快速发展,尤其是在数值天气预报领域,已经被国际上多个业务中心作为业务算法进行使用[3]。中国国家气象局[4],美国国家大气研究中心[5~6],英国国家天气预报中心[7]以及欧洲中尺度天气预报中心[8]都将变分同化算法作为核心业务算法实现了业务化。在数值天气预报领域的成功实践证明了变分同化算法的可行性和正确性。目前同化算法除了气象领域之外,在海洋[9~11],大气污染物预测[12~15],地质土壤[16~18]等领域都得到了较大的发展。
2 变分同化基本原理
假设n维向量xt表示某一物质扩散的真实状态,n维向量xb表示背景场状态,m维向量y表示观测向量,H表示观测算子,是观测值与真实状态之间的纽带函数。同时,我们用εb表示背景场的误差,εo表示观测场的误差,那么我们便可以得到:
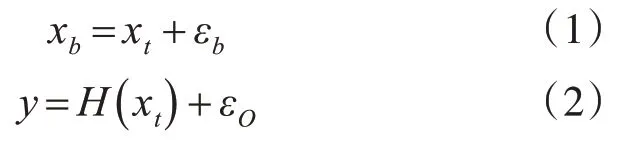
假设误差准确,且估计无偏,那么εb、εo的数学期望为0,则背景误差协方差矩阵为

观测误差协方差矩阵为

在数据同化中,我们一般认为背景与观测是两个相互独立的事件。假设Pb(x)表示背景场的概率分布,Po(x)表示观测值的概率分布,且两者相互独立,那么这两个概率分布的乘积就是它们的联合概率密度函数,也就是我们所求分析场的概率分布,即:
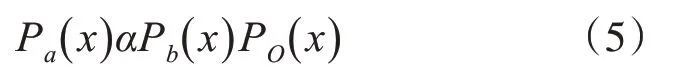
根据最大似然估计原理,极大似然估计值就是使Pa(x)取得最大值时的变量值,也就是所求的分析值。在实际应用中,如果不知道实际的气象条件,扩散状态,一般假设为各向同性,其概率则要服从高斯分布,概率密度函数也应为高斯函数,则:
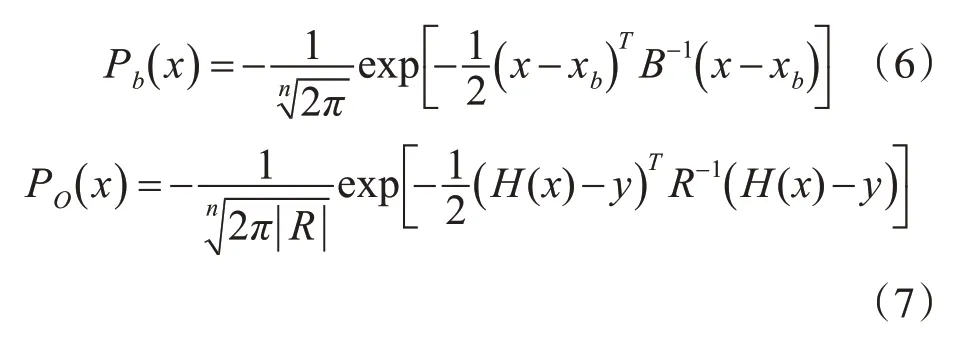
两者的概率密度相乘,便可以得到分析值的概率密度函数。由于我们所要求的是使联合概率密度函数取极大值时的函数值,并不是为了去极大值。所以,一般来说,为了简单计算,我们一把将联合概率密度函数取对数值。同时,消去负号,使求极大值问题转变为求极小值问题,也是简便计算的常用方法之一。以此为基础,构造出的目标函数为
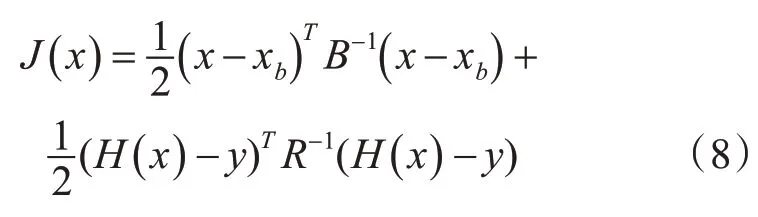
上式的含义是表示分析场与背景场的距离以及分析场与观测场的距离。该函数的值越小,说明距离越小,说明分析值与观测值之间的“距离”越小。
式中:x表示分析值,xb为背景场,B为背景误差协方差,R为观测误差协方差,y为观测值,H为观测算子。
3 误差协方差矩阵
误差是整个同化过程中不可避免的。数学角度看,可以把同化过程理解为最小化误差的过程。误差在同化开始前主要体现在背景误差协方差矩阵B上。由于实际的操作过程中,不管是所设定的背景场数据,亦或是由各种型号的侦察装备所得到的观测场数据,甚至是模型本身都不是绝对准确的,都是有误差的。但是由于很难确定“真值”xtrue到底是多少,就无法得知背景误差和观测误差到底是多少。同时当误差一直存在于同化的整个过程中时,整个分析过程都是带有误差的,这个分析误差是上述三种误差在同化过程中相互作用的结果。
一般情况,误差协方差矩阵假设观测误差与背景误差不相关,即:

式中:εb为背景误差;εo为观测误差,T为矩阵转置。
在实际分析中,这也是完全合理的假设,背景场参量与观测场参量相互独立。
3.1 背景误差协方差矩阵
背景误差协方差矩阵表示预报误差的概率分布函数,是一个高斯型的函数分布。同化系统所产生的分析场参量大概只有15%来自观测资料,而剩余的85%均来自背景场[19]。在物理意义上,背景场是同化前该地域的状态场,它将同化循环中的观测数据不断融合进最新的分析场。
背景误差协方差矩阵在同化中具有很重要的作用:首先它具有信息传递的作用,尤其是在观测资料短缺的地区,分析增量的形状几乎完全由协方差决定,矩阵的相关性决定了从观测点到周围空间的信息传播;其次具有信息平滑的作用,在观测资料稠密地区,它的相关性也决定了信息的平滑程度;它还能体现各个参量之间的平衡关系,比如高度位势和风场之间的平衡。
与卡尔曼滤波数据同化方法[20~21]不同的是,变分法理论上并不能很好地处理背景误差协方差矩阵B,因此背景项的设立就显得尤为重要[22~23]。
变分公式中的B是这样定义的:
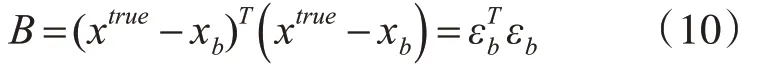
式中xtrue代表真值,εb为背景误差,很多时候B矩阵也表示为
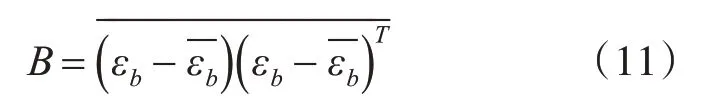
不难看出,B矩阵是正定对称矩阵,而且特征值均为非负值。
假设背景误差为向量(e1,e2,e3),其背景误差协方差矩阵可写成:
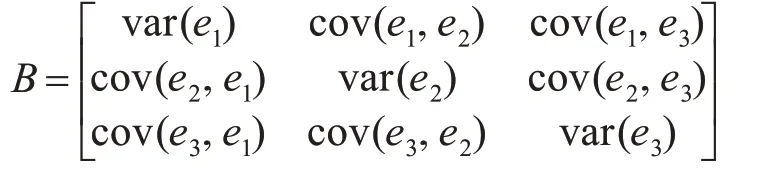
3.2 观测误差协方差矩阵
观测误差协方差矩阵包含关于观测误差的统计信息。对观测系统来说,不同位置上的观测误差在统计上是相互独立的。观测误差一般包括观测算子、仪器和代表性误差。
观测算子误差主要是因为对两种不同种类的数据之间联系的理解不足导致,主要出现在非直接观测中。
代表性误差一般来源于两方面:一是模型不完美,得不到完全准确的测量;二是有限的模型分辨率,这类误差的减小可以利用高密度观测,提高模式分辨率。
仪器误差是出厂时带有的,一般会带有数据参数,考虑设备老化等实际情况可以对参数进行适当调整。除此之外,也鲜有好的解决办法。
一般而言,对R的处理较简化,在观测之间相互独立情况下,将其简化为对角矩阵,方便计算。
4 变分同化误差系数影响分析
在变分同化模块中,同化质量受到多种不同因素的影响,其本身各类参数的影响最大。在上一节的基础上,通过数据模拟方法[24]分析背景场参量和观测场参量对同化质量的影响。
简单起见,在同一高度层进行仿真试验,只考虑同一种化学物质一个平面层内的连续扩散,不考虑不同观测设备所获取的数据格式的不统一,简化观测算子为单位矩阵或单位向量。
设定统一的试验先验条件:界定危害区域为10km×10km,风向为0°,风速固定为3m/s,大气稳定度为D级,扩散参数以GB/T为准,迭代次数1000次。假定同化窗口0时刻为扩散发生4小时之后,以模型首次预报值加上随机误差生成背景场,以模型后续预报值作为真值,将预报值加上20%随机误差生成观测值。
4.1 背景误差系数对同化的影响分析
保证以上条件不变,设定观测均方差为1,选取算法为四维变分数据同化算法,简单分析背景场对同化结果的影响。
首次试验,设定初始背景协方差矩阵为二维单位矩阵,同化结果走势如图1所示。
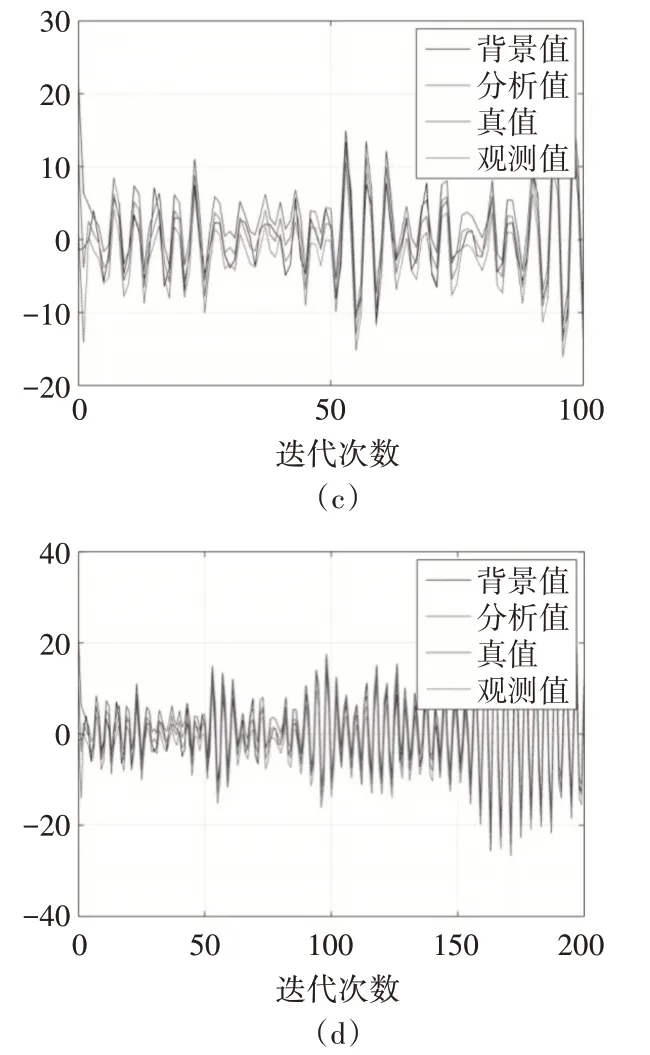
图1 首次试验同化结果图
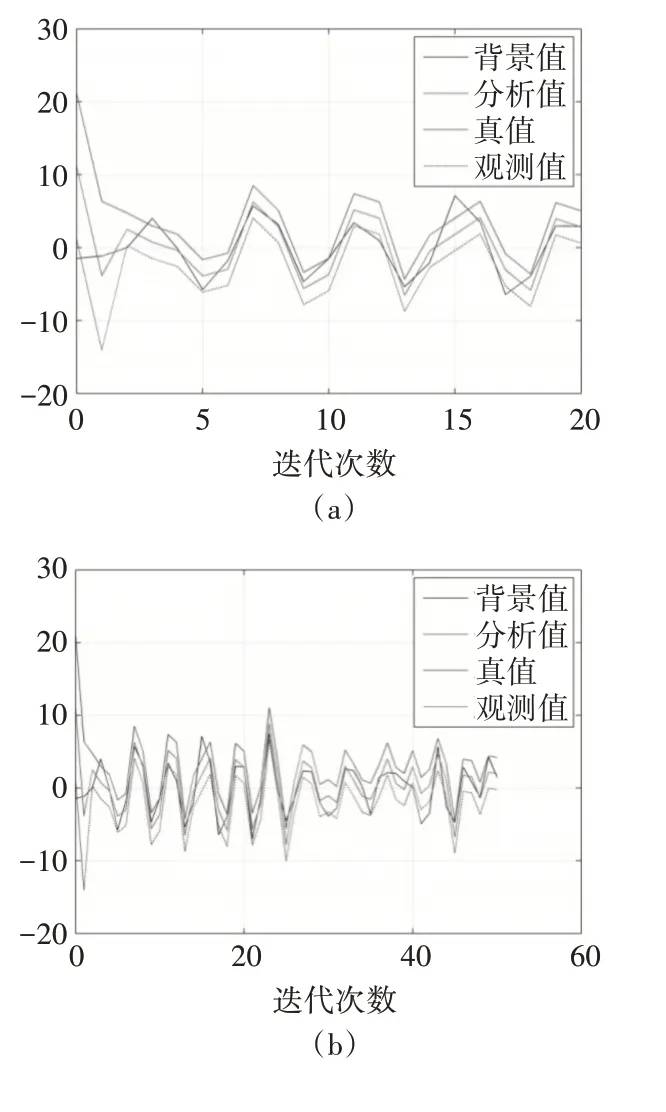
图中可以看出,在20次迭代的时候,分析值明显比观测值和背景值更加接近真值,起到同化效果。随着迭代次数的不断增多,各条曲线间的差异便不是那么容易可以看出来了。在200次迭代的同化图中,不难看出,基本已经达到了同化效果,并且具有收敛性。这与图2的误差以及方差走势图也是相一致的。
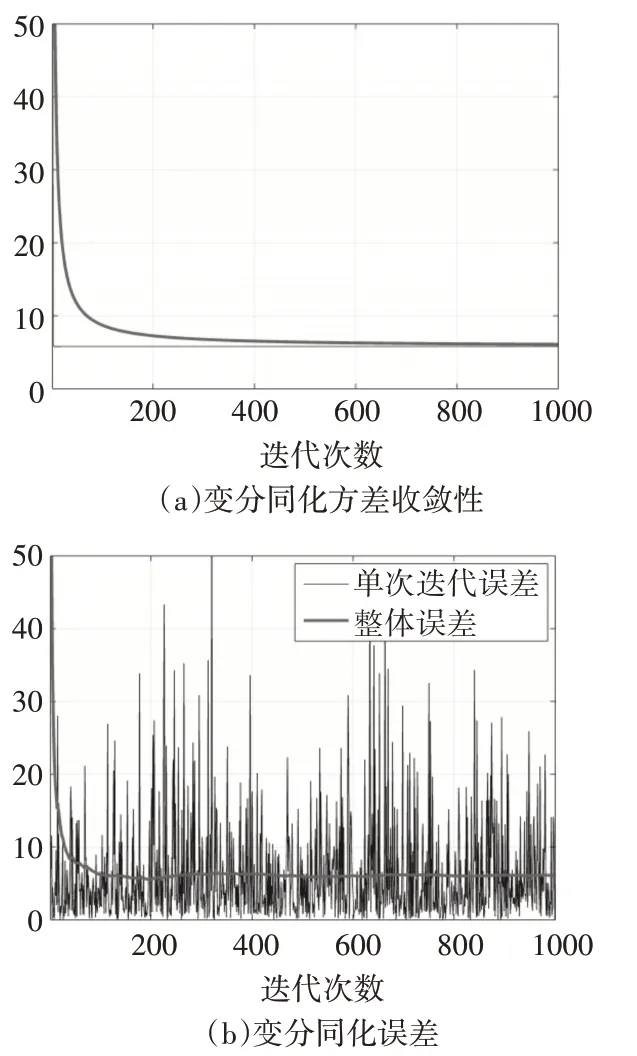
图2 首次同化误差变化图
从图中可以明显看出在200次迭代后,误差及方差基本收敛。
第二次试验,调整初始背景场误差系数,设置为首次的0.5倍大小,再次进行数值模拟试验。结果如图3所示。
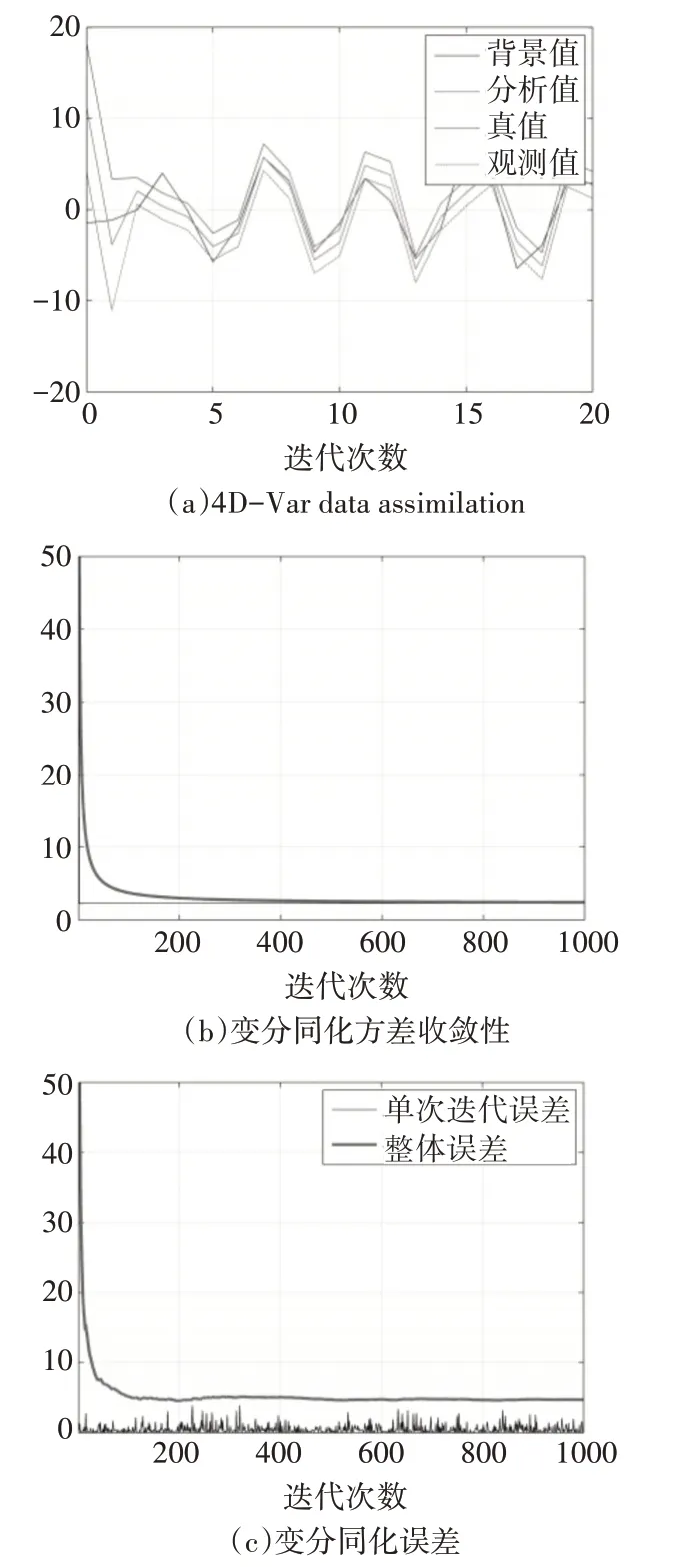
图3 第二次背景参数影响分析试验
从第二次的试验结果可以看出,背景初始误差的变化会导致同化精度提高,但是并不影响同化的误差以及方差的收敛性。
第三次试验,调整背景场误差系数,设置为首次的0.2倍大小,再次进行数值模拟试验。结果如图4所示。
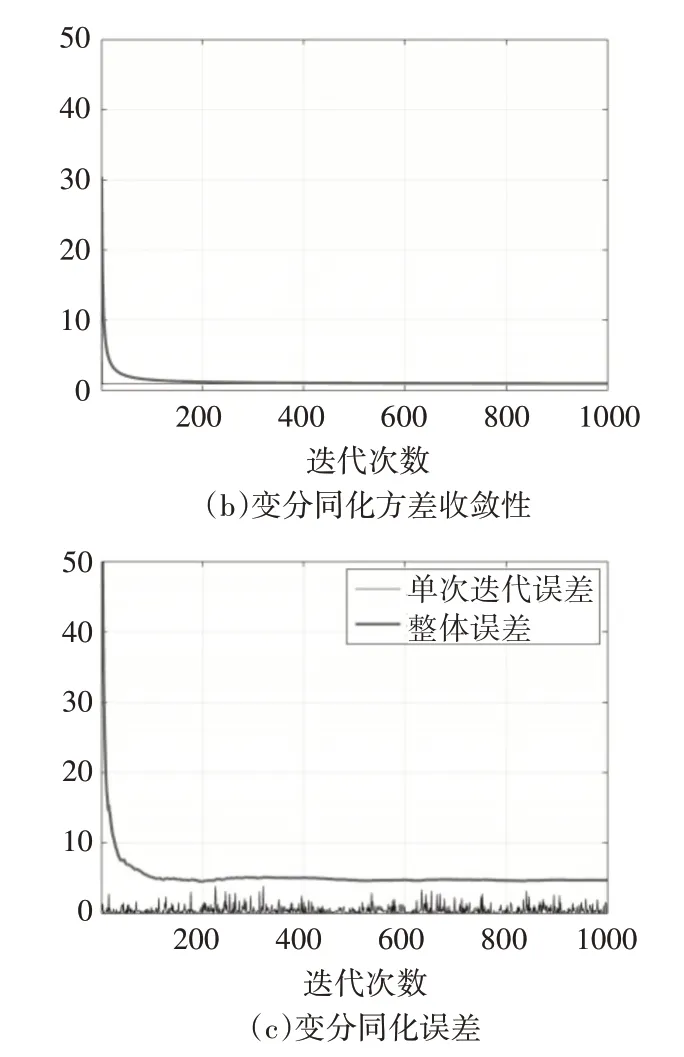
图4 第三次背景误差系数影响分析试验
从第三次试验的同化结果可以看出,背景误差系数的改变会影响初始同化的精度,但是不会影响同化过程的收敛性。
图5是三次背景场参数试验同化效果对比图。
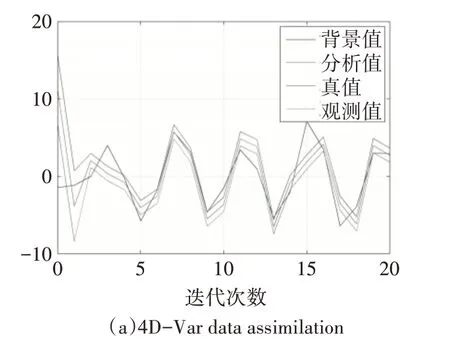
由图5可以看出,改变初始的背景场误差系数,会对同化的效果和精度产生影响。当背景误差系数减小的时候,同化精度会有提高。
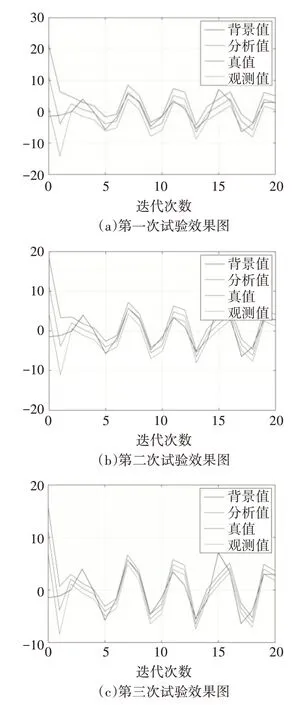
图5 背景误差系数分析试验对比图
但是,从以上三次试验分析来看,背景场误差系数对同化结果造成影响的同时,并不会影响整个同化窗口内的收敛性,三次试验基本都在200次迭代之后开始收敛。
4.2 观测误差系数对同化的影响分析
保持初始设置条件不变,选取算法为三维变分同化算法,设置B为对角矩阵,对角线元素为误差方差,设定其为固定值0.4。这次试验分析同化后的两个小时内的同化情况。
由于观测误差协方差矩阵R为对角阵,首次试验设定观测误差均方差为0.1。
试验结果如图6所示。
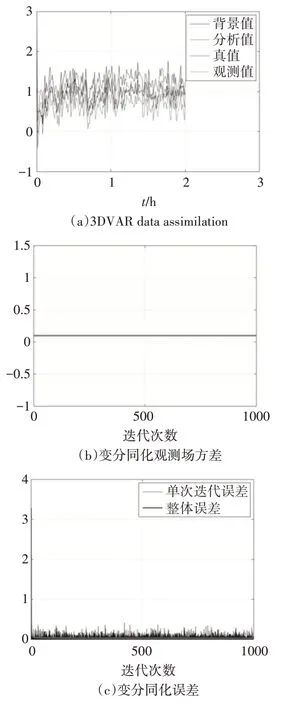
图6 首次观测参数影响分析试验
从首次试验的结果来看,由于背景误差系数设定为固定数值,所以整体试验的收敛性较好,基本20次迭代后已成收敛状态。同时,由于观测误差协方差矩阵的性质为对角矩阵,且对角线元素也已经设置,所以观测场方差的图形是一条直线。
第二次试验,保持其他参数不变,上调观测误差系数为0.25,结果如图7所示。
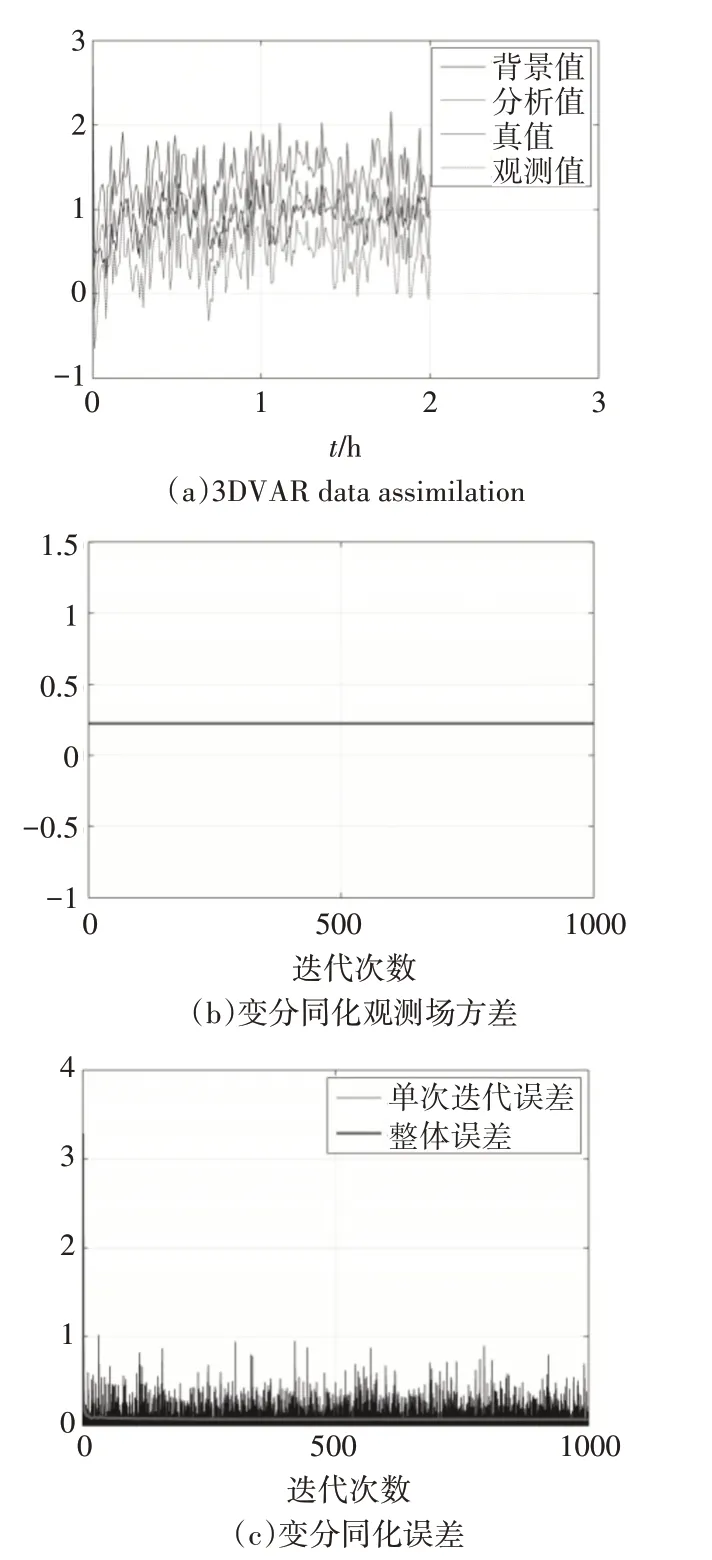
图7 第二次观测参数影响分析试验
就第二次的试验结果来看,误差系数加大,同化的稳定性加大,同化的波动加大,但是收敛性并没有改变。
第三次试验,保持其他参数不变的基础上,上调观测误差参数为0.30,结果如图8所示。
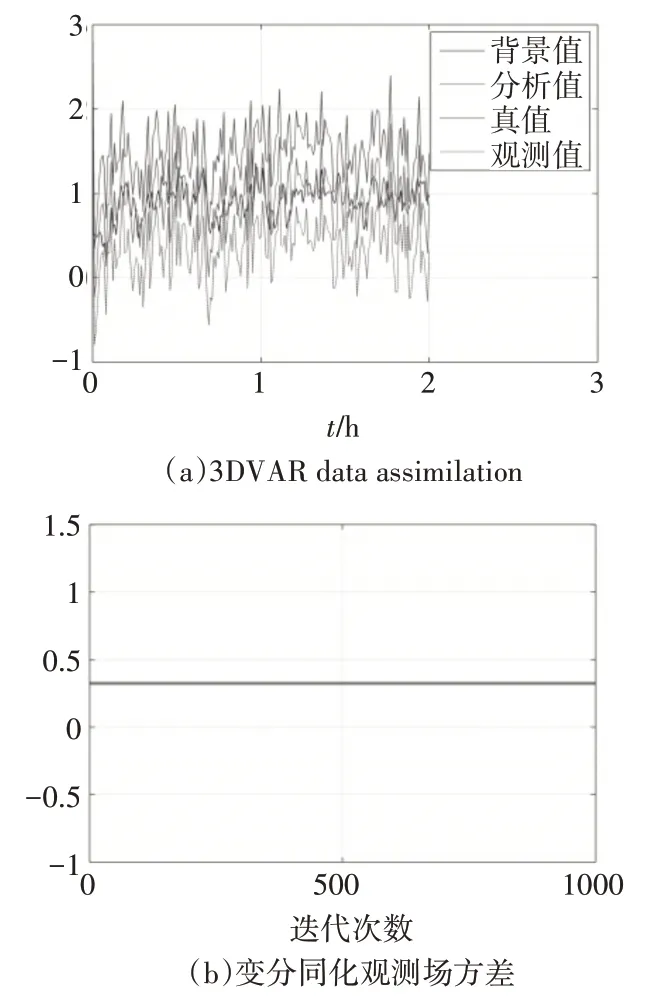
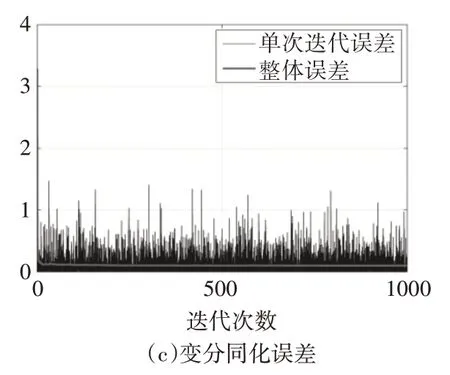
图8 第三次观测响参数分析试验
第三次同化的结果来看,同化窗口内波动加大,收敛性不变。
图9是三次同化效果的对比图。
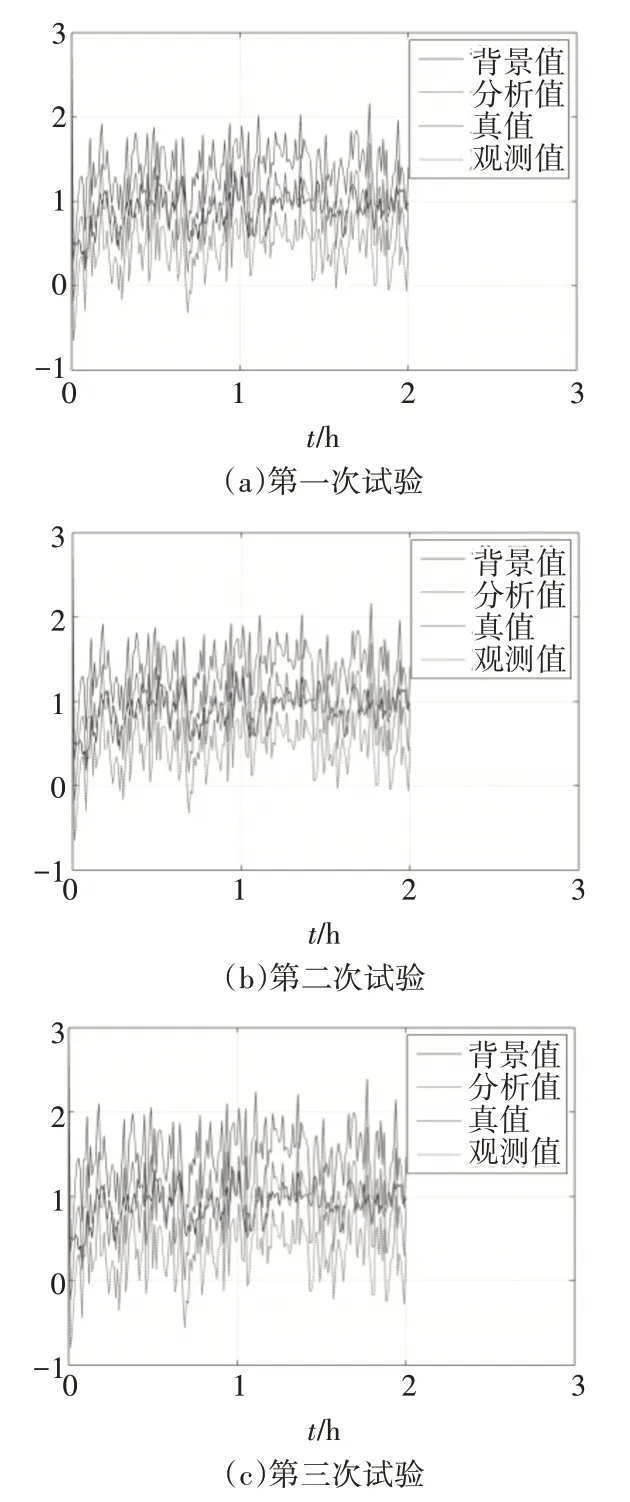
图9 观测参数分析试验对比图
对比来看,观测参数的变化会影响同化的质量,误差越大,波动越大,效果越差。同时,参数改变不影响收敛性。
5 结语
通过对两种不同的误差参数的试验结果来看,背景误差系数和观测误差系数的改变会影响同化的质量,误差系数越大,同化窗口内的波动越大,效果越差,这也是符合常识认知的;但是,通过对比发现,背景场参数变化对同化的影响程度要高于观测参数的影响,这也是为什么在实际工作中,认为背景场更加重要的原因;本研究的结果也进一步表明,不管是背景参数还是观测参数的改变,误差系数的大小都不影响同化的整体收敛性。
