织金县暴雨强度公式的研究和分析

2022-11-09赵庭飞柯莉萍张东海施倩雯

气象水文海洋仪器 2022年3期

赵庭飞，柯莉萍，张东海，秦霞，杨洋，施倩雯

(1.织金县气象局，织金 552100；2.威宁县气象局，威宁 553100；3.贵州省气候中心，贵阳 550002；4.金沙县气象局，金沙 551800)

0 引言

全球气候变暖导致极端强降雨时常发生，城市内涝现象日益明显[1]。在“6.28”织金县特大暴雨事件中，过程降雨量刷新了本站1958年以来历史记录，县城降雨量达181 mm，县城上游金凤最大降雨量达306 mm，织金县城出现严重城市内涝，城镇内涝造成6.02万人受灾，织金县城主干道的积水有1 m多深。近年来，织金县城市建设的规模逐渐发展扩大，住房密集，混凝土覆盖层显著增加，雨水不透水，城市雨水蓄水调节能力减小，洪水灾害风险评估低，导致内涝灾害频发[2]，对正常生产模式产生重大的影响。

朱思诚等专家建议，要想解决现代城市洪涝日益突出的问题，要进一步加强排水基础设施的建设，并适当提高排水系统管道建设的设计标准。根据要求，城市建设雨水系统的设计必须按照雨水分离系统的标准进行，但其相关经费的预算直接与雨水设计流量的可靠性密不可分，因此合理的选择暴雨强度计算公式直接关系到设计流量计算。根据调查显示，织金县目前没有合适本地的暴雨强度公式，因此文章结合历年来降雨情况，从实际出发，本地化研究分析织金县暴雨强度公式。

1 资料与方法

1.1 资料来源及样本建立

利用织金县国家基本气象站1991—2020年逐分钟降雨资料，采用年最大值法[3]，选取5 min，10 min，15 min，20 min，30 min，45 min，60 min，90 min，120 min，150 min，180 min共11个时段年最大降雨量，建立合适的暴雨强度公式统计样本。

1.2 暴雨强度公式拟合方法

在频率分布函数中选取Pearson-3型函数、Cubei型函数和指数函数[4]，对统计样本数据进行修正。最终确定最优函数对数据样本不同重现年份的计算式进行参数拟合，得出重现期、暴雨强度和降雨历时三者之间的关系。使用最小二乘法对非线性的计算式进行处理，从而对暴雨强度公式的各个参数进行拟合，并通过拟合参数误差分析的结果判断是否满足所规定的精度要求。

2 样本资料的理论频率分布曲线调整

利用中国气象局采用的降雨强度计算系统，利用Pearson-3分布曲线、指数分布曲线和Cubei分布曲线对样本数据进行修正，最终通过判断准确性确定最优的频率分布曲线，给出重现期P、降水强度i和降水持续时间t之间的关系(图1)。从图1可以看出，通过调整Pearson-3分布的变差系数和偏态系数，理论频率曲线与实际频率曲线基本重合。

图1 Pearson-3型分布曲线

根据图1拟合结果，计算出Pearson-3型函数拟合的绝对误差为0.076 mm/min，相对误差为6.59%。由表1计算出指数分布曲线拟合的绝对误差为0.080 mm/min，相对误差为6.22%。由表2计算出Cubei分布曲线拟合的绝对误差为0.067 mm/min，相对误差为4.98%。比较精度检验结果，Cubei分布曲线优于Pearson-3型和指数分布曲线，因此选择匹配效果较好的Cubei分布曲线进行调整。根据Cubei分布曲线的调整结果，表3给出了重现期P、降水强度i和降水历时t的关系。从表3可见，同一个降水历时中，降水强度i随着重现期P增加逐渐增大。

表1 指数分布曲线参数表1)

1)指数函数：X=a×lnT+b，X表示某一段时段内的降雨强度，a为离散参数，b表示上升或者下降。

表2 Cubei分布曲线参数表1)

1)Cubei分布公式为X=-a×(ln(ln(P/(P-1)))+b，X表示某一段时段内的降雨强度，a表示尺度参数，b表示位置参数。

表3 重现期、降雨强度、降雨历时(P-i-t)表

3 暴雨强度公式的推求

3.1 单一重现期暴雨强度公式的推求

根据2014年国标版降雨强度公式定义，使用Cubei分布曲线来延长资料样本[5]，求解参数推求降雨强度公式，得到单一的重现期暴雨强度公式，求解结果见表4。

表4 织金县单一重现期暴雨强度公式

注：t为降雨历时/min，取值为5～180 min。

3.2 区间参数公式的拟合

根据表4中的暴雨强度公式可知，只能确定某一固定重现期的暴雨强度，而任意重现期的降雨强度却无法获得，为了解决这一问题，引入暴雨强度区间公式[6，7]。

根据目前研究暴雨强度公式通用的区间参数公式，将重现期1～100 a分为1～10 a和10～100 a两个区间，利用单一重现期暴雨强度公式拟合方法，求得1～100 a区间内任意一个重现期的暴雨强度公式，求解结果见表5。

表5 织金县暴雨强度区间参数公式

3.3 暴雨强度总公式

使用Cubei函数延长资料样本，采用最小二乘法[8-11]求解出暴雨强度总公式。暴雨强度总公式拟合结果：

(1)

式中，q为设计暴雨强度(升/秒/公顷)；P为重现期；t为降雨历时(min)，取值为5～180 min。

通过暴雨强度总公式绘制降水曲线，从图2降水量随时间的变化曲线可知：在某一固定的重现期内，降水量随着降水时间的增加而增加；不同的降水时段，在50 a前，降水量随着重现期的增加而增加；在50 a后，降水量随着重现期的增加，不同时段逐渐趋于某一个值，不再增加。

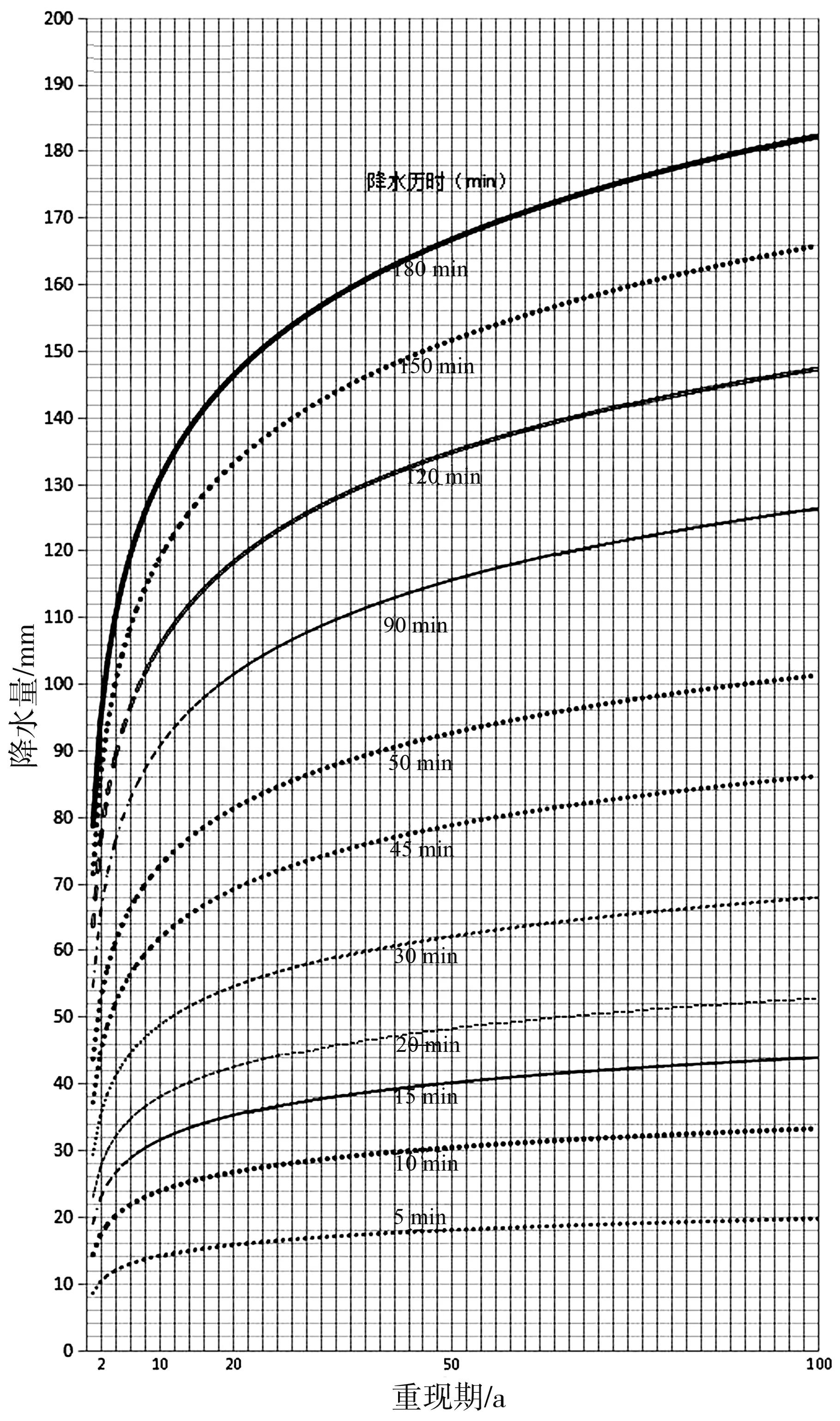
图2 织金县降水变化曲线

4 暴雨强度公式的误差检验

为保证计算结果的准确性，对降雨强度计算结果的准确性进行了检验，对重复周期为2～20 a的降雨强度和计算出的降雨量的绝对误差进行了检验。强度理论值与实测值计算取平均值，相对误差与GB50014-2006《室外排水设计规范》规定的精度进行比较。一般降雨强度区域的绝对方差不超过0.05 mm/min，高降雨强度区域的相对均方差不超过5%。

在2～20 a计算的区间公式降雨强度的绝对方差为0.048 mm/min，相对方差为3.27%。同时，计算总公式的绝对方差为0.067 mm/min，相对方差为4.98%，符合国标建议的误差标准。由此可见，暴雨强度区间公式比暴雨强度总公式更有优势。