载人登月近距离交会制导策略分析
2022-11-09王晓磊解永春王高阳
刘 涛, 王晓磊, 解永春, 王高阳, 李 骥, 杨 巍
(1.北京控制工程研究所, 北京 100190; 2.空间智能控制技术国家级重点试验室, 北京 100190)
1 引言
Apollo 计划将人类送上月球,开创了载人深空探测的序幕[1]。 2004 年,美国又提出星座计划(Constellation Program),宣布将再次登上月球,并建立月球基地[2]。 虽然该计划于2010 年被终止,但标志着载人登月以及建立月球基地等成为月球探测的未来发展方向。 目前,美国正在实施月神计划(Artemis Program),准备在建设近直线Halo轨道(Near-Rectilinear Halo Orbit)空间站的基础上,于2024 年让人类重新踏上月球[3]。
中国则通过嫦娥系列探测器历时13 年圆满完成无人月球“绕、落、回”探测任务。 在月球建造基地并以此作为中转站,将为实施载人深空探测提供极大的便利。 而实施月球轨道交会对接可大幅减小从地球或月面发射航天器的规模,有效降低对起飞运载能力的要求。 因此,月球轨道交会对接技术是实施载人登月以及载人深空探测的支撑性技术之一。
交会对接任务可分为2 个阶段:①远距离交会将追踪器从入轨初始轨道导引到相距数十公里近距离交会段要求的预定轨道,设计重点是实现快速性;②近距离交会则指从相距数十公里直至对接的过程,设计重点是控制精度和安全性[4]。 近距离交会制导是整个交会对接策略设计的核心。 受制于复杂的空间环境和有限的地面测控支持能力,相较于近地轨道任务,载人登月在任务类型、快速性、自主性和安全性等方面,都有全新要求。 而与无人月球探测任务不同,载人登月涉及多种交会对接任务类型,尤其需要适应近圆和椭圆等不同轨道;此外,确保航天员安全是载人任务的第一要务,必须设计应急交会方案以提高安全性。
本文针对载人登月交会的上述特点,通过对月球轨道环境下不同交会制导律的性能进行比较,对近距离交会制导策略进行分析研究,提出兼具通用性和高性能要求的交会制导策略,为工程实践提供参考。
2 交会制导律
在近距离交会策略设计中,通过设定若干停泊点,由追踪器在停泊点间进行转移,逐步接近目标器。 为便于轨控求解,交会制导仅将停泊点位置作为制导目标,抵达停泊点后再进行目标速度控制。
目前,可用于近距离交会段的交会制导律主要包括:基于绝对轨道参数的LAMBERT 制导、基于相对轨道参数的C-W 制导、视线制导以及T-H制导等,其中LAMBERT 制导和T-H 制导可用于椭圆轨道目标交会。 LAMBERT 制导基于航天器绝对轨道动力学模型进行设计,求解较为复杂,但具有通用性强的优势,可兼顾远程交会和近程交会轨控,并可应用于椭圆轨道和近圆轨道交会。美国Apollo 工程和航天飞机任务均采用LAMBERT 制导进行交会轨道控制;T-H 制导是一种基于椭圆轨道近距离线性化相对动力学模型的制导律,其计算量较C-W 制导大,且求解过程中需要利用到目标航天器的轨道真近点角。 目前,还没有T-H 制导应用于工程实践的报道;C-W 制导是一种基于圆轨道近距离线性化相对动力学模型的制导律,由于其求解简单,且仅需利用目标器轨道角速度,因而在各国的交会对接飞行任务中得到广泛使用[3];视线制导是一种基于球坐标系相对动力学模型的制导律。 由于球坐标间的耦合较为严重,所以视线制导多应用于停泊点接近末端的交会轨控,其优势在于可依据接近距离逐步施加减速控制,进而提高交会过程的稳健性。 视线制导已在俄罗斯和中国的交会对接飞行任务中得到使用[4]。
2.1 LAMBERT 制导
航天器交会问题可以归结为LAMBERT 问题,即给定航天器的初始位置r1和终端位置r2以及转移飞行时间Δt, 确定飞行轨道。 对于LAMBERT 问题的求解,一般的思路是选择独立的迭代变量,根据飞行时间定理建立控制方程组,迭代计算以获得一定精度的解。 对LAMBERT 问题的研究方兴未艾,对应的算法有多种。 本文采用Battin 普适迭代算法设计LAMBERT 制导。
Battin 普适迭代算法以x作为独立的迭代变量,对应的方程组如式(1)所示[5]:
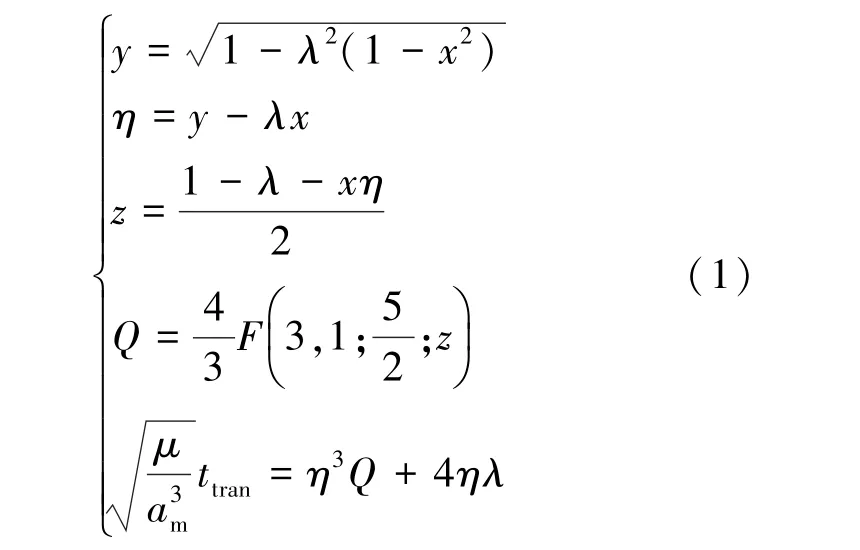
采用New-Raphson 方法进行数值求解得到x,迭代函数如式(2)、(3)所示:
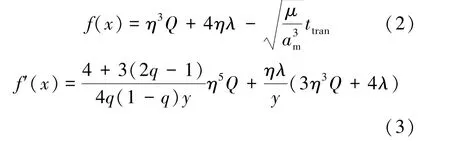
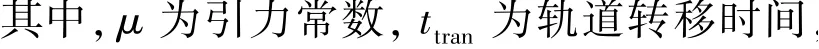

LAMBERT 制导基于二体轨道动力学进行设计,轨道摄动会对制导精度产生不利影响。 为此,Thompson 等[6]提出以二体轨道LAMBERT 制导解作为初值,采用精确轨道动力学外推进行制导结果预测,据此进行制导目标修正,形成预测迭代LAMBERT 制导算法。 该算法在提高制导精度的同时,会带来计算量的大幅增加,这对实际星载应用造成了困难。

2.2 T-H 制导
T-H 制导是一种基于椭圆轨道近距离线性化相对动力学模型的制导律。
所采用轨道坐标系OoXYZ的定义为:原点Oo为航天器的质心,OoX轴为位置方向且背离月心,OoZ轴指向轨道角速度方向,OoY轴与OoZ、OoX轴构成右手系。
依据二体轨道得到相对动力学模型,并对引力加速度差采用Taylor 分解,且仅保留一阶项,得到如式(6)所示的相对动力学模型:
以目标器轨道真近点角为自变量,可以求解得到相对状态,满足式(7):

即
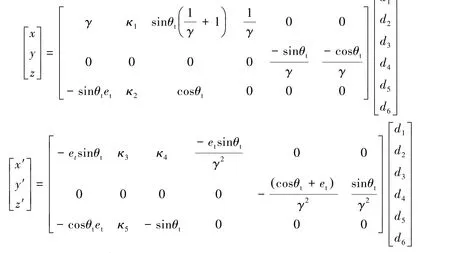
其中,et为目标器轨道偏心率,d,κi,γ的具体形式见文献[5]。
采用状态转移方程得到任意时刻的相对状态与初始状态间的关系,见式(8):
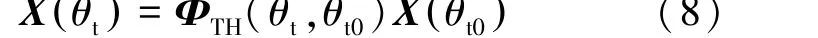


2.3 C-W 制导
在目标器轨道系(VVLH 系)中,C-W 方程的具体形式见式(11)[4]:
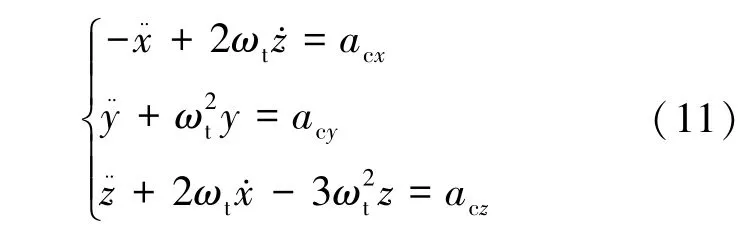
其中,ωt为目标航天器轨道角速度,aci(i=x,y,z) 为追踪器控制加速度。
以相对位置和相对速度为状态量,可以求解得到转移方程式(12):

3 寻的段交会制导分析
寻的段为近距离交会过程的初始阶段,追踪器通常从距离目标器后下方数十千米处开始抵达目标器附近的停泊点。 本文以Apollo11/12 所采用的寻的段交会策略为例[1],对采用不同制导律的交会轨道控制性能进行比较分析。
Apollo11/12 在所执行的月面起飞交会对接任务中采用了共面椭圆交会方案(Coelliptic Rendezvous)。 经远程导引阶段后,轨道为共面、同心的椭圆轨道,并且具有如下特性[7]:①目标器和追踪器半长轴at,ac和偏心率et,ec满足atet=acec;②轨道高度差满足at-ac=ΔH,ΔH为设计值;③轨道拱线方向重合。 具体设计中,寻的段初始轨道高度差设定为28 km;在首脉冲设计中,Apollo 采用了推力视线指向策略,即首脉位置对应的视线角为26.6°,转移时间对应目标器掠过的相位角为130°,这使得首脉冲指向恰好沿着视线方向,从而避免调姿[8]。 寻的段飞行过程中施加了2 次中间修正脉冲,脉冲间隔约为15 min。
分析中,轨道动力学计算中采用LP165P 引力摄动模型,考虑70 阶非球形引力摄动以及地球和太阳三体引力摄动。 初始轨道参数如表1 所示(目标器初始偏心率et在0.001~0.03 间遍历)。

表1 寻的段初始轨道Table 1 Initial orbit elements of the homing phase
LAMBERT 制导中需要对目标器轨道进行外推计算,设定星载算法考虑20 阶非球形引力摄动以及地球和太阳引力摄动。
仿真结果见表2~表5 以及图1~图3,可以得出:①偏心率小于0.005 时,C-W 制导精度和燃料消耗性能优于T-H 制导;反之,则T-H 更优;此外,T-H 制导在偏心率小于0.001 时性能欠佳,应避免使用。 ②不同偏心率时,LAMBERT 制导误差变化很小,燃料消耗最优,但其制导精度并无优势。③LAMBERT 制导基于二体绝对轨道模型设计,未考虑摄动影响,这是其制导误差的主要来源。 若动力学采用二体轨道时,则LAMBERT 制导的精度非常高(表5);而T-H 和C-W 制导基于相对动力学模型设计,近距离时两航天器轨道摄动接近,差分后轨道摄动项残留很小,制导模型精度更高,这是其精度相对LAMBERT 制导高的原因。
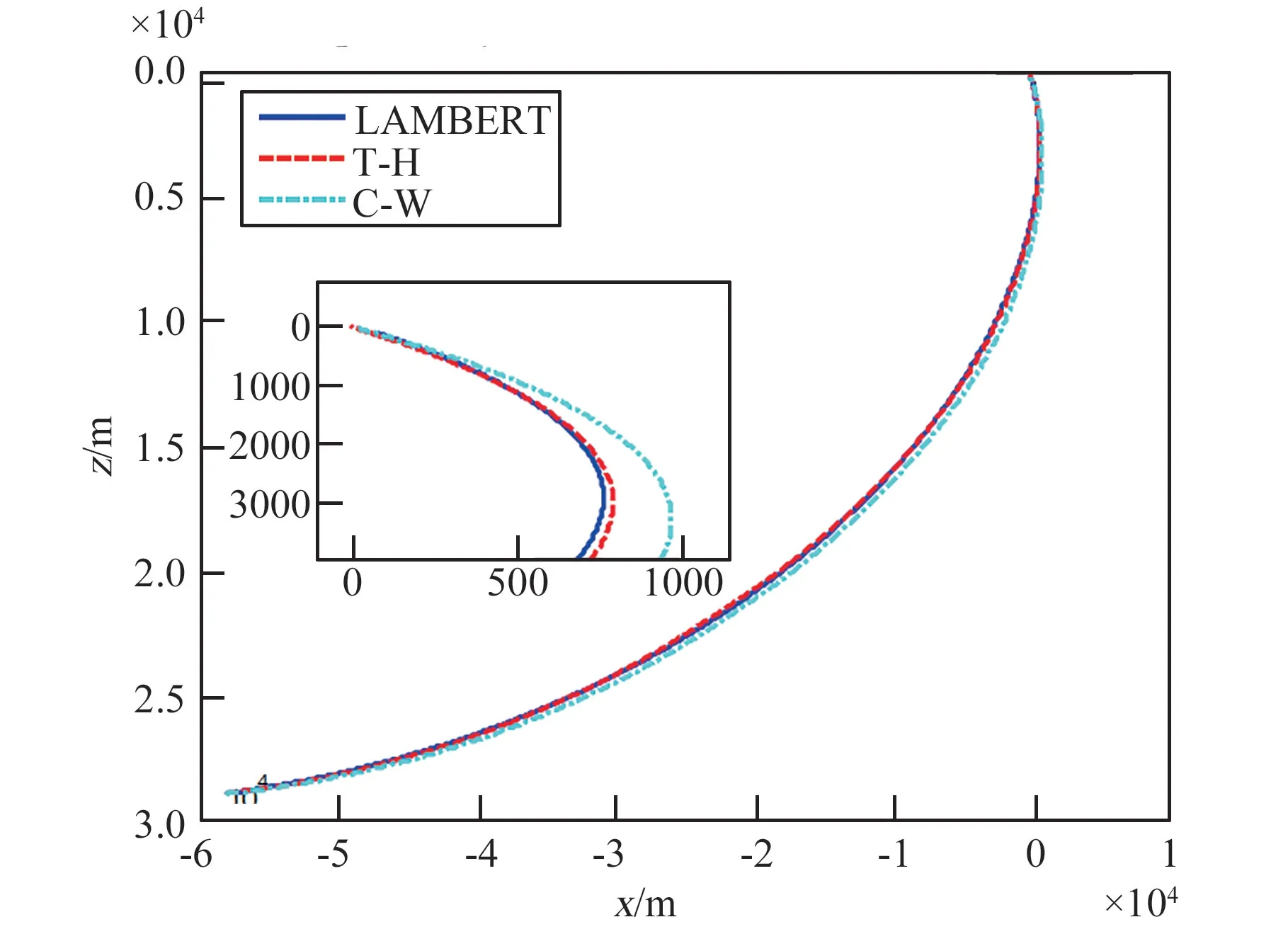
图1 寻的段交会飞行轨迹(e=0.01)Fig.1 The flight trajectory in homing phase (e=0.01)

图3 寻的段不同偏心率时的制导总速度增量Fig.3 Total velocity increment of the homing phase under different eccentricities
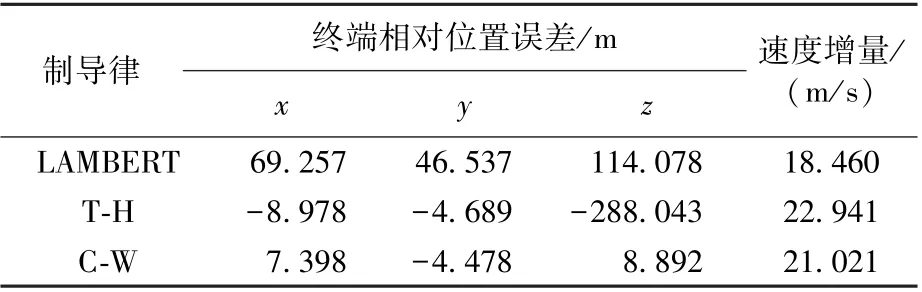
表2 寻的段e=0.001 时的制导结果Table 2 Guidance result of the homing phase (e=0.001)
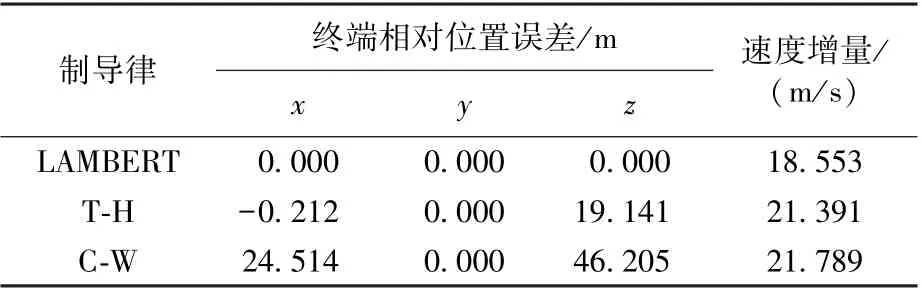
表5 寻的段e=0.01 时的制导结果(二体轨道)Table 5 Guidance result of the homing phase with two body orbit (e=0.01)
LAMBERT 制导的优势在于可适用于不同偏心率工况,性能稳定且燃料消耗最优;劣势为由于未考虑轨道摄动,制导精度相对较低;而C-W 制导更适用于小偏心率工况,大偏心率时其性能下降较快;T-H 制导则在偏心率大于0.005 时性能优于C-W 制导,但是其在小偏心率时性能欠佳。
综合分析,寻的交会的目标位置通常较目标器还有一定距离,可以容忍一定制导误差。 LAMBERT 制导的通用性好,精度也满足工程设计要求,综合性能相对更优。
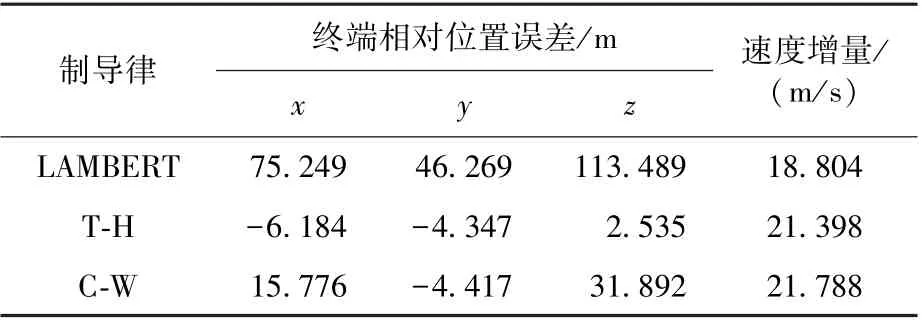
表3 寻的段e=0.01 时的制导结果Table 3 Guidance result of the homing phase (e=0.01)

表4 寻的段e=0.03 时的制导结果Table 4 Guidance result of the homing phase (e=0.03)

图2 寻的段不同偏心率时的制导终端位置偏差Fig.2 Guidance position deviation in homing phase under different eccentricity
4 接近段交会制导分析
接近段为近距离交会过程的第二阶段,追踪器通常从距离目标器数千米处经过停泊点间的转移(可以包括绕飞)直至捕获数百米处的对接走廊止。 以下以目标器-V-BAR 处5 km 停泊点转移至0 m 过程为例,对采用不同制导律的交会性能进行比较分析。 初始轨道参数如表6 所示(et在0.001~0.03 间遍历)。
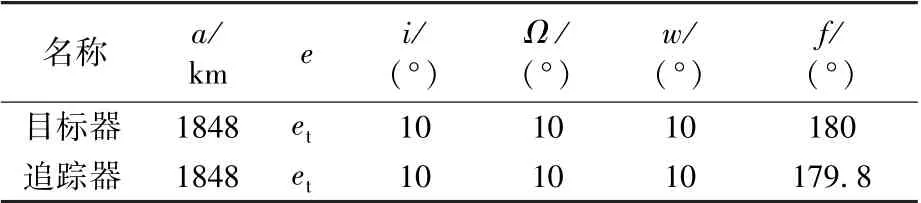
表6 接近段初始轨道设定Table 6 Initial orbit elements of the approaching phase
仿真结果见表7~表9 以及图4 ~图6。 可以得出:①偏心率小于0.01 时,C-W 制导性能优于T-H 制导;反之,则T-H 更优;②不同偏心率时,LAMBERT 制导误差变化很小,但其制导精度和燃料消耗均无优势。
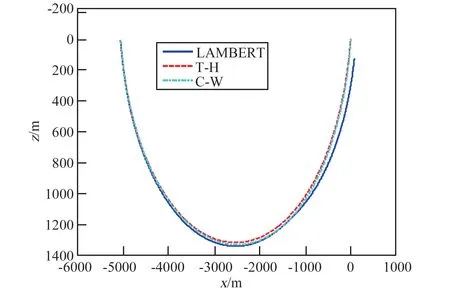
图4 接近段飞行轨迹(e=0.01)Fig.4 The flight trajectory in approaching phase (e =0.01)
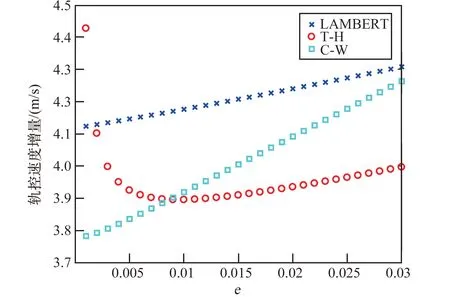
图6 接近段不同偏心率时的制导总速度增量Fig.6 Total velocity increment of the approaching phase under different eccentricities
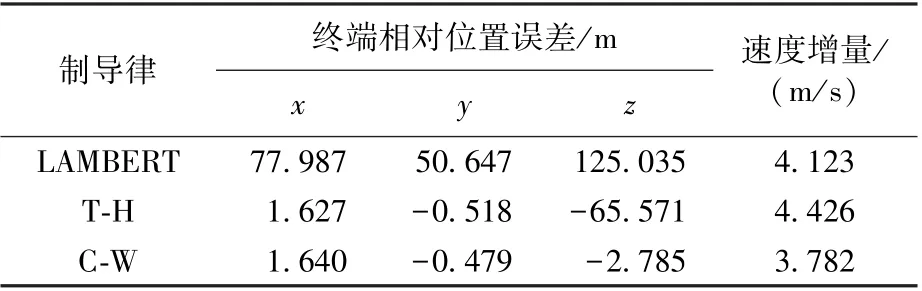
表7 接近段e=0.001 时的制导结果Table 7 Guidance result of the approaching phase(e=0.001)
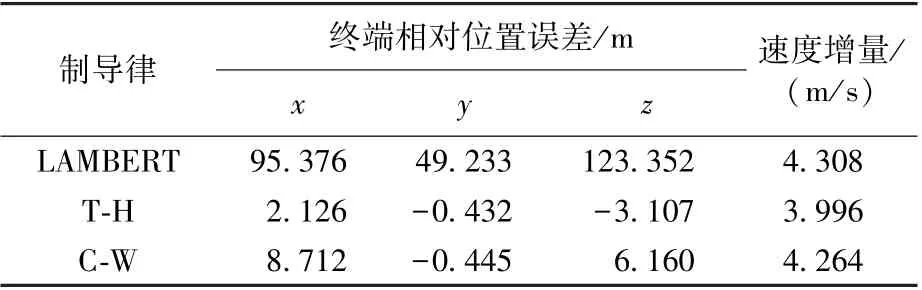
表9 接近段e=0.03 时的制导结果Table 9 Guidance result of the approaching phase (e =0.03)
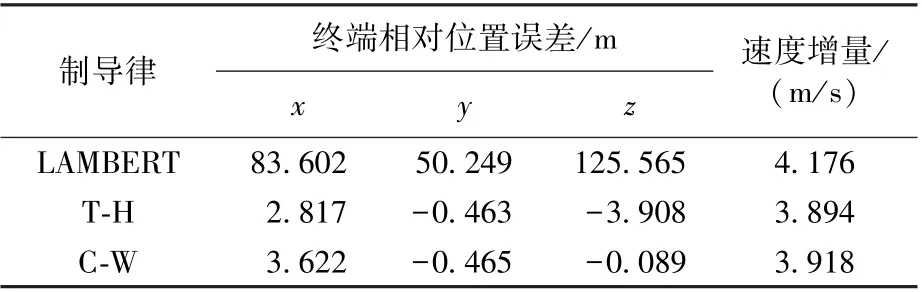
表8 接近段e=0.01 时的制导结果Table 8 Guidance result of the approaching phase (e=0.01)
LAMBERT 制导的优势在于可适用于不同偏心率工况,性能稳定,但是制导精度明显较低;而C-W 制导更适用于小偏心率工况,大偏心率时其性能有一定下降;T-H 则在偏心率大于0.01 时性能优于C-W 制导,但是其在小偏心率时性能欠佳。
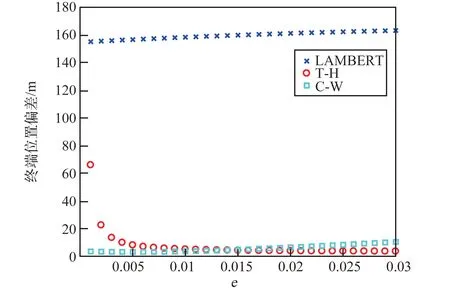
图5 接近段不同偏心率时的位置偏差Fig.5 The guidance position deviation in approaching phase under different eccentricities
综合分析,LAMBERT 制导精度较差并不适合接近段使用;T-H 制导则在小偏心率时性能下降过大,通用性欠佳;而C-W 制导则具备通用性,虽然精度有一定下降,但是仍满足工程应用要求,综合性能相对更优。
5 近距离交会制导策略设计
载人登月交会制导方案设计需要兼顾正常交会和应急交会,必须适应近圆和椭圆等不同轨道类型,满足快速性、自主性和安全性要求。 同时,由于星载计算资源有限,这就要求交会制导方案兼具通用性并确保制导精度。
可以看到,LAMBERT 制导因未考虑轨道摄动,其制导精度并不具优势。 但是LAMBERT 制导可适应不同轨道类型,具备良好的通用性。 因此,在对制导误差容忍度相对较高的寻的段,可将LAMBERT 制导作为主份方案。
在接近段,由于相对距离较近,对制导精度的性能要求更为严格,制导精度更高的T-H 制导和C-W 制导更为适用。 虽然T-H 制导在椭圆轨道时性能优异,但是在近圆轨道时其性能下降显著,兼容性较差。 而C-W 虽然在椭圆轨道时性能会下降,但是通过增加修正频次,对应的增加一定燃料消耗,可确保精度满足任务要求;其次,考虑到深空任务自主定轨难度大,相较于T-H 制导中需要利用目标器轨道真近点角,C-W 制导仅需利用目标轨道角速度,这对定轨精度要求要低得多;再次,C-W 制导求解更加简单,也更利于星载制导算法设计。 可见,C-W 制导的兼容性和制导精度综合性能在接近段更具优势。
综上分析,采用分段使用LAMBERT 制导和C-W 制导的综合制导策略,是载人登月任务近距离交会的可行方案。
表10 给出了不同目标器轨道偏心率时,近距离综合制导策略的终端位置误差和轨控速度增量,图7 给出了交会轨迹。 偏心率越大则终端位置误差越大,同时轨控速度增量也越大。 但是,终端位置误差均小于20 m,而轨控速度增量的散布也小于1 m/s。
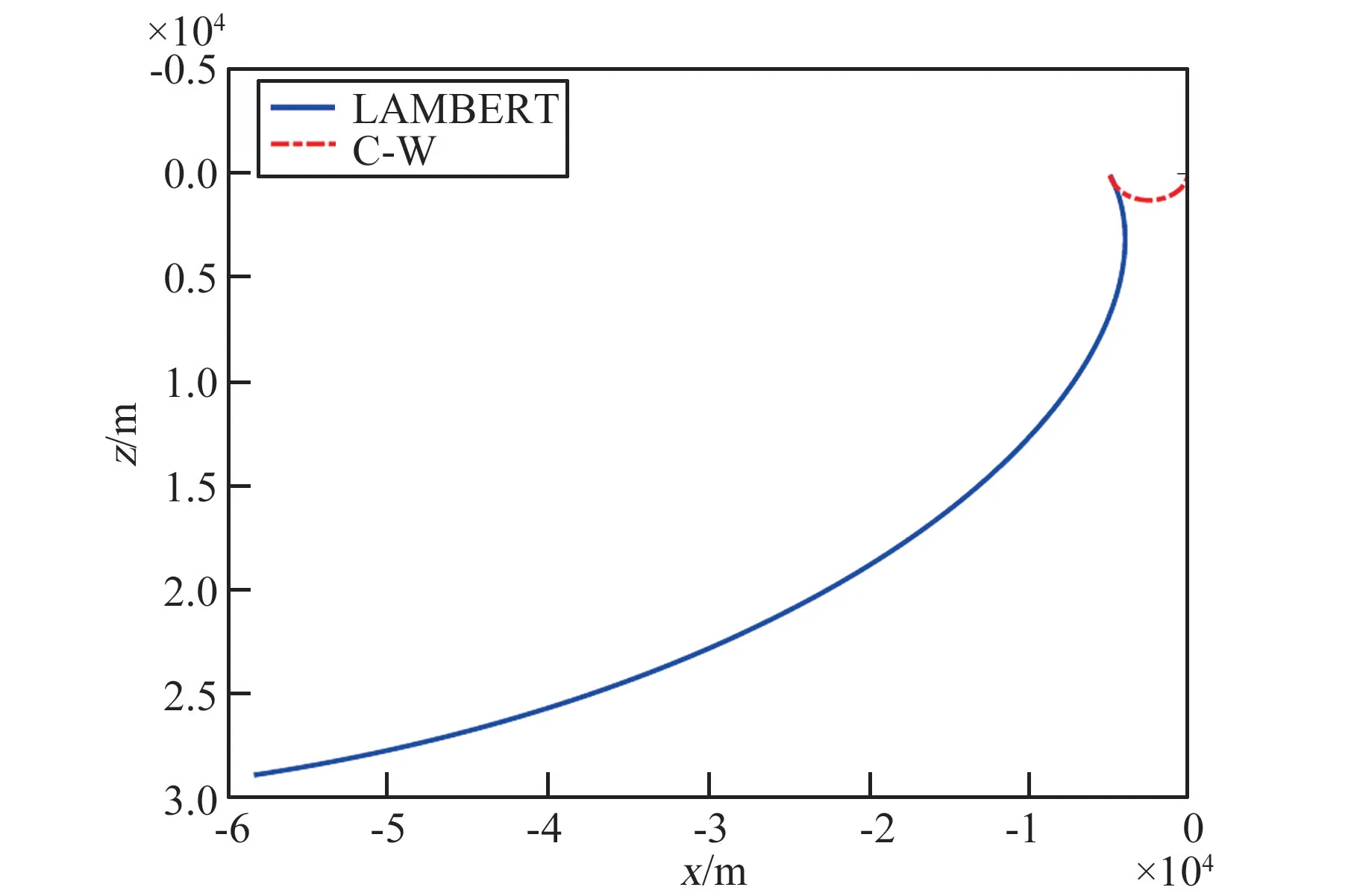
图7 近距离交会飞行轨迹(e=0.01)Fig.7 Flight trajectory of the near-range rendezvous phase (e=0.01)
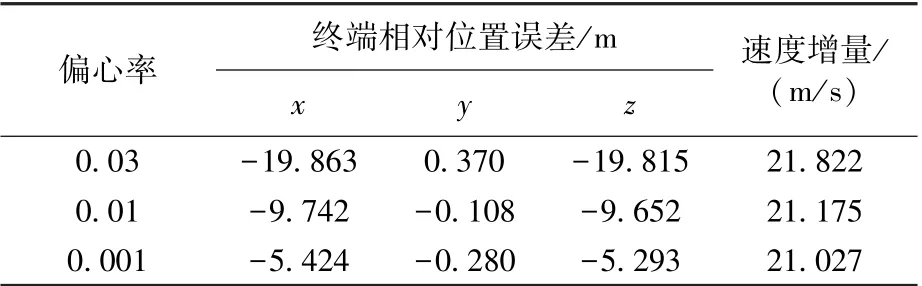
表10 近距离交会段综合制导结果Table 10 Guidance result of the near-range rendezvous phase
可见,采用分段使用LAMBERT 制导和C-W制导的综合制导策略,在不过多增加燃料消耗的同时,可适应不同目标器轨道。
6 结论
本文针对载人登月交会需要适应近圆和椭圆等不同轨道,同时对快速性、自主性和安全性要求极高的特点,通过月球轨道环境下就不同制导律性能进行分析比较,对近距离交会制导策略进行设计。 研究表明:在寻的段交会任务中,LAMBERT 制导的通用性好,精度也满足工程设计要求,综合性能更具优势;而在接近交会任务中,CW 制导的通用性更好,综合性能更优。 因此,合理采用LAMBERT 制导结合C-W 制导分段使用的综合制导策略是载人登月任务近距离交会的可行方案。
随着深空自主导航精度的提高和星载计算能力的不断提升,采用LAMBERT 制导、C-W 制导、T-H 制导,设计性能更为优越的近距离交会综合制导策略将成为可能,后续会继续深入研究。
