数据挖掘中的分类算法研究

文/孟磊 刘静萍

当前，我们所处的时代是数据爆炸式增长的时代，来自于社会生产、工程、医疗、商业及科学研究领域的数据每天都在增长。这些数据类型多样、数据量巨大、价值密度低、增长速度快, 只有对这些数据进行合理的组织和分析才能发掘其背后的应用价值[1]。数据挖掘的诞生就是为了对海量数据进行分析、分类并提取有价值的信息，为研究者做出进一步预测和判断提供数据基础[2]。分类是数据挖掘中一个重要的研究领域，其研究内容是在一群已经知道类别标号的样本中，训练一种分类器，让其能够对某种未知的样本进行分类。分类算法的分类过程就是建立一种分类模型来描述预定的数据集或概念集，通过分析由属性描述的数据库元组来构造模型。分类的目的就是使用分类器对新的数据集进行划分，其主要涉及分类规则的准确性、过拟合、矛盾划分的取舍等。解决分类问题的方法很多，单一的分类方法主要包括：决策树、贝叶斯、神经网络、K近邻、支持向量机和基于关联规则的分类等，另外还有用于组合单一分类方法的集成学习算法，如Bagging和Boosting等。

常用分类算法分析

从大量历史数据中挖掘并找出隐含的规律是分类算法的特性之一，可用于预测或者分析。更具体地说，分类是构建一个函数，输入样本数据，输出可期望的结果。分类的目标是使学到的函数很好地适用于“新样本”，而不仅仅是在训练样本上表现得很好。学到的函数适用于新样本的能力，称为泛化能力。

朴素贝叶斯分类

朴素贝叶斯分类(NBC)是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法。先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的输出Y。

设有样本数据集D={d1,d2,…,dn}，对应样本数据的特征属性集为X={x1,x2,…xd}，类变量为Y={y1,y2,…,ym}, 即D可以分为ym类别。其中x1,x2,…xd相互独立且随机，则Y的先验概率为Pprior=P(Y), Y的后验概率为Ppost=P(Y|X)，由朴素贝叶斯算法可得，后验概率可以由先验概率Pprior=P(Y)、证据P(X)类条件概率P(Y|X)计算出：

朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为下式：

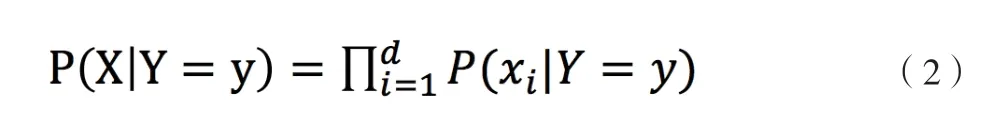
由以上两式可以计算出后验概率为：

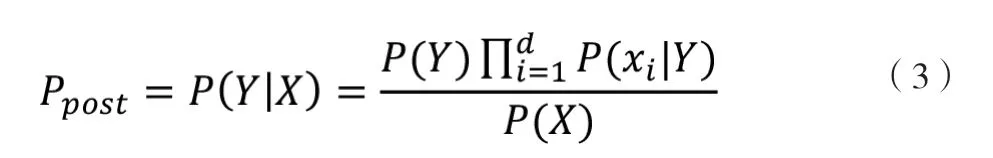
由于P(X)的大小是固定不变的，因此在比较后验概率时，只比较上式的分子部分即可。因此可以得到一个样本数据属于类别yi的朴素贝叶斯计算：

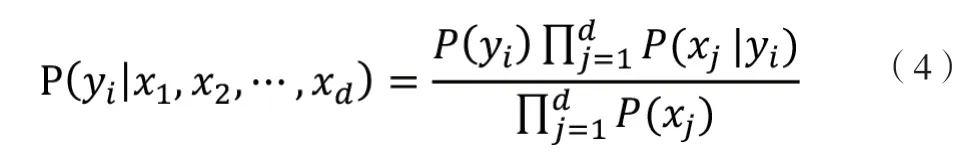
朴素贝叶斯方法的特点是结合先验概率和后验概率，既避免了只使用先验概率的主观偏见，也避免了单独使用样本信息的过拟合现象。朴素贝叶斯发源于古典数学理论，有着坚实的数学基础。该算法是基于条件独立性假设的一种算法，当条件独立性假设成立时，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。该算法的优点是：逻辑简单，易于实现，算法所需估计的参数很少；算法对缺失数据不太敏感，具有较小的误差分类率；算法性能稳定，健壮性比较好。缺点是：在属性个数比较多或者属性之间相关性较大时，NBC模型的分类效果相对较差；算法是基于条件独立性假设的，在实际应用中很难成立，故会影响分类效果。

K近邻

K近邻(K-Nearest Neighbor，KNN)分类算法是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：在特征空间中，如果一个样本附近的K个最近（即特征空间中最邻近）样本的大多数属于某一个类别，则该样本也属于这个类别。

如图1所示，有两类不同的样本数据，分别用红色的小正方形和绿色的圆形表示，而图正中间的蓝色的菱形所标示的数据则是待分类的数据。也就是说，现在，我们不知道蓝色的数据是从属于哪一类（红色小正方形或者是绿色圆形）。下面，我们就要解决这个问题：给这个蓝色的菱形分类。

图1 K近邻算法示意

如果K=3，蓝色菱形最近的3个邻居是1个绿色圆形和2个红色小正方形，少数从属于多数，基于统计的方法，判定蓝色的待分类点属于红色的正方形一类。如果K=6，蓝色菱形最近的5个邻居是2个红色正方形和3个绿色的圆形，少数从属于多数，基于统计的方法，判定蓝色的待分类点属于绿色的圆形一类。

因此，我们看到，当无法判定当前待分类点是从属于已知分类中的哪一类时，依据统计学的理论看它所处的位置特征，衡量它周围邻居的权重，而把它归为或分配到权重更大的那一类。这就是K近邻算法的核心思想。该算法的优点是：算法简单，有效适用于样本容量比较大的类域的自动分类；主要依靠周围有限的邻近的样本，而不是依靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。缺点是：算法计算量较大，算法需要事先确定K值；算法输出的可解释不强；算法对样本容量较小的类域很容易产生误分。

支持向量机

支持向量机（Support Vector Machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的学习算法就是求解凸二次规划的最优化算法。

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，如图2所示。对于线性可分的数据集来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。

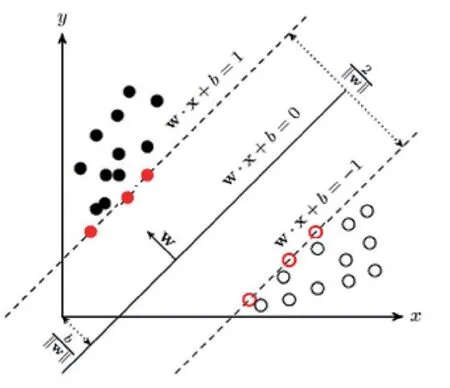
图2 SVM算法示意

在分类问题中给定输入数据和学习目标X={X1,X2,…XN}，y={y1,y2,…,yN}，其中输入数据的每个样本都包含多个特征并由此构成特征空间而学习目标为二元变量表示负类和正类。若输入数据所在的特征空间存在作为决策边界的超平面，将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1。

则称该分类问题具有线性可分性，w, b参数分别为超平面的法向量和截距。满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：

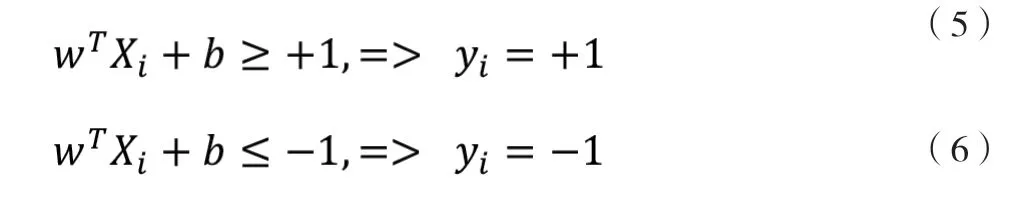
所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离被定义为边距，位于间隔边界上的正类和负类样本为支持向量。

SVM算法是建立在统计学习理论基础上的机器学习方法，通过学习算法，SVM可以自动寻找出对分类有较好区分能力的支持向量，由此构造出的分类器可以最大化类与类的间隔，因而有较好的适应能力和较高的分准率。该算法的优点是：有很高的分准率和泛化性能；能很好地解决高维问题，对小样本情况下的分类问题效果较好。缺点是：对缺失数据敏感，对非线性问题没有通用解决方案，得谨慎选择核函数来处理。

分类器的创建

分类算法在生产和生活中有很多应用场景，如：日常事务[3][4]、医疗[5]、交通运输[6]、建筑工程[7]、金融[8]等领域。分类算法的应用极大地提高了相关领域的工作效率，节省了大量的人力资源。本节阐述了朴素贝叶斯、K近邻和SVM三种算法在日常生活中的应用。

对数据集进行分析

要在程序中使用这些数据集，需要了解数据的详细信息。通常数据集由数据集名称、实例个数、属性个数、属性名称和分类名称构成。本文的实验部分选用了UCI数据集中的三种，分别是红酒数据集、鸢尾花数据集和乳腺癌数据集。这三组数据集都可以用来做分类测试，其属性如表1所示。

表1 数据集属性表

以鸢尾花数据集为例，数据集打开后可以看到文本的排列：每行5个数以逗号分隔，共150行，每行的前4列分别对应4个属性值，而最后一列为每个数据所属类别。

生成训练数据集和测试数据集

在创建分类算法模型时，需要对模型进行评判，否则无法知道模型的分类是否准确。因此必须将数据集分为两个部分：一部分称为训练数据集，用以学习数据的特征属性，这部分数据需要人工标定，为数据生成标签；另一部分称为测试数据集，用来检验模型的性能如何，不需要人工标定。

Python中的 scikit-am机器学习库中，有一个 train_test_split 函数，可以把数据集拆分成训练集和测试集。其工作原理是： train_test_split函数将数据集进行随机排列，在默认情况下将其中75%的数据及所对应的标签划归到训练数据集，并将其余25%的数据和所对应的标签划归到测试数据集。

使用分类算法建模

对分类算法建模可以用Python中scikit-learn机器学习库中的分类器，也可以自己编程建模。本节采用朴素贝叶斯算法，以红酒数据集作为测试集和训练集进行建模，来说明算法的建模过程，如图3所示。

图3 朴素贝叶斯分类的流程

对新样本分类进行预测

分类模型建好之后，就可以用于对新的样本分类进行预测。不过在此之前，最好先用测试数据集对模型进行打分，这就是创建测试数据集的目的。测试数据集不参与建模，但是可以用模型对测试数据集进行分类，然后和测试数据集中的样本实际分类进行对比，当吻合度越高，模型的得分会越高，说明模型的预测越准确，满分是1.0。

Python仿真结果分析

本文的实验部分选择了三种算法和三组数据集，将不同的数据集分成训练集和测试集，用训练集来构建分类器，并用测试集来验证分类器的准确率。

表2是三种算法在三种数据集上的分类准确率情况。

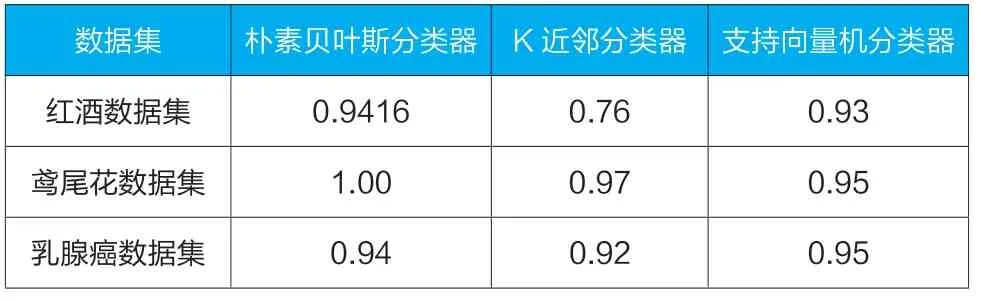
表2 三种算法的分类准确率

从表2中的数据可以看到，三种算法在数据集的分类上准确率都较高。其中高斯朴素贝叶斯分类器在符合正态分布的数据集上分类准确率最高；K近邻分类器分类准确率对数据集的依赖性最强，也即模型的泛化能力是最弱的；本文中支持向量机分类器的内核为RBF（径向基函数）内核，在三种算法中分类效果最为稳定，模型的泛化能力是三种分类器中最强的。

本文通过对数据挖掘分类算法中的三种经典算法，朴素贝叶斯算法、K近邻算法和SVM算法的深入研究和对比发现：朴素贝叶斯依据概率论的原理建模，算法逻辑简单，易于实现，对缺失数据不太敏感，具有较小的误差分类率，但是在属性个数比较多或者属性之间相关性较大时，NBC 模型的分类效果相对较差。K近邻算法是最简单的分类算法，缺点是算法计算量较大，需要事先确定K值。SVM算法有很高的分准率和泛化性能，能很好地解决高维问题，对小样本情况下的分类问题效果较好，缺点是对缺失数据敏感，对非线性问题没有通用解决方案，得谨慎选择核函数来处理。本文的实验部分选用了三组数据集来验证三种算法的分类准确率，实验结果表明,三种算法都能很好地解决分类问题，但都有一定的局限性，在具体应用中需要根据算法在特定数据集上的优势和劣势选择相应的算法去解决。