Budyko假设在灌区耗水估算的适用性
2022-11-09林一凡霍再林汪超子张成龙韩振中崔静
林一凡,霍再林*,汪超子,张成龙,韩振中,崔静
▪水土资源与环境▪
Budyko假设在灌区耗水估算的适用性
林一凡1,霍再林1*,汪超子1,张成龙1,韩振中2,崔静2
(1.中国农业大学水利与土木工程学院,北京 100083;2.中国灌溉排水发展中心,北京100054)
【目的】验证Budyko假设在农业灌区的适用性,为准确估计灌区实际耗水提供新方法。【方法】基于全国282个大中型灌区2010—2017年的灌溉量、降水量、潜水蒸发量及实际蒸散发量,验证了Budyko假设对农业灌区耗水估算的适用性,对比分析不同气候条件下的估算准确性。【结果】Budyko假设框架下考虑灌溉水及潜水蒸发量的傅抱璞公式能够较好地估算灌区年度耗水,估算与实测之间的相对误差小于21.7%。比较而言,该公式在种植结构和灌溉制度较为稳定的湿润区具有更好的适用性。同时,受气象条件、灌区输配水条件、土壤质地、作物种植结构等要素的影响,Budyko水热耦合模型的参数具有显著的区域分布特征,表现为随湿润程度增加而增大。【结论】Budyko假设在全国农业灌区年耗水量估算中具有很好的潜力。
Budyko假设;灌区;耗水;气候
0 引言
【研究意义】灌区是全球农业生产的重要载体,也是重要的耗水主体。作为水循环和能量平衡联系的纽带,灌区耗水在陆面水热耦合中起到重要作用。同时,准确估算灌区耗水,对于区域水资源规划与管理具有重要的意义。【研究进展】灌区耗水受到气象条件、灌溉用水、土壤条件及作物种植等多因素影响,在时空上具有很强的差异性。一般来说,年尺度灌区耗水可采用水量平衡、过程模拟等方法来确定[1]。其中水量平衡由于其结构简单及普适性强,成为灌区耗水的重要计算方法。苏联学者Budyko提出流域实际蒸散发受到陆面水分供给()、能量供给(0)间平衡关系影响,即Budyko假设[2]。多年来,许多学者根据气象数据、径流数据以及水量平衡原理,拟合得到了不同形式的水热耦合平衡方程,证明了Budyko假设的成立[3-6],并成功应用于流域耗水估算及水平衡分析。传统的Budyko水热平衡方程需满足如下假设:其一是流域为自然且封闭,降水是流域内蒸散发的唯一来源;其二是在较长的时间跨度和较大的空间范围内,流域内的蓄水量变化可以忽略不计。近年来针对较小时间尺度和非稳态的情况,众多学者引入了包括地下水埋深、土壤水储量及灌溉水量在内的一系列变量,极大地拓宽了Budyko假设的适用范围[7-11]。不同于流域,灌区受灌溉活动影响,其水热平衡关系较为复杂。韩松俊等[12]验证了新疆绿洲灌溉农业区水热平衡关系满足Budyko假设。Simons等[13]采用Budyko公式计算了巴基斯坦印度河流域灌区耗水量。针对地下水浅埋灌区,陈航等[14]提出了考虑灌溉和潜水蒸发的灌区尺度Budyko理论框架,并成功应用于内蒙古河套灌区。【切入点】受灌区水文气象、土壤条件、灌排条件、种植结构等影响,Budyko假设在不同气候区灌区的适用性还不明确。【拟解决的关键问题】本文以我国不同气候区的282个大中型灌区(2010—2017年)为研究对象,验证了Budyko假设在农业灌区的适用性,分析了不同气候区实际蒸散发估算精度的差异,并在此基础上分析不同气候条件下模型参数的分布特征。
1 材料与方法
1.1 研究数据
1.1.1 灌区数据
本研究选取全国范围内282个大中型灌区2010—2017年间的数据,数据来源于中国灌溉排水发展中心,具体数据包括灌区有效灌溉面积、灌溉水利用系数(全国灌溉水利用系数测算结果)、毛灌水量及地下水埋深,其中灌溉水利用系数为灌入田间可被作物吸收利用的水量(净灌溉用水量)与灌区从水源取用的灌溉总水量(毛灌溉用水量)的比值。根据干湿指数()将全国划分为干旱区(<0.20)、半干旱区(0.20≤<0.50)、半湿润区(0.50≤<1.00)和湿润区(≥1.00)4个气候区。其中,西北地区大部分为干旱区,半干旱区包含内蒙古和青海新疆一带,半湿润区主要分布在华北和东北地区,湿润区包含我国南方地区和部分东北地区。

表1 不同气候区样点灌区的基本数据统计
本研究选择由中国气象数据网提供的气象日数据集V3.0中的839个国家级气象站点,并通过GIS定位连接到邻近的大中型样点灌区,研究时段为2010—2017年,所用气象数据包括降水量、逐日最高和最低气温、日照时间、2 m高度风速、相对湿度等。潜在蒸散发0的计算采用FAO-56推荐的Penman-Monteith公式[15]。
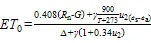
式中:0为参照作物腾发量(mm);n为作物表面上的净辐射(MJ/(m2·d));为土壤热通量(MJ/(m2·d));为平均气温(℃);2为2 m高处的风速(m/s);s为饱和水汽压(kPa);a为实际水汽压(kPa);sa为饱和水汽压差(kPa);Δ为s-关系曲线的切线斜率(kPa/℃);为湿度计常数(kPa/℃)。
1.1.2 灌区实际年耗水数据
一般来说,灌区年耗水量难以准确获得。研究中灌区年耗水由灌区遥感耗水数据得到。由于研究中缺少确切的灌区实际边界图,难以获得灌区准确范围内的遥感耗水,研究中采用灌区等效面积内的农田耗水作为灌区耗水。利用GIS以灌区位置为圆心构建与灌区面积相等的圆形缓冲区代替灌区边界,结合2015年中国土地利用现状遥感监测数据提取灌区中耕地的栅格以提取灌区耗水。本研究从MOD16A3数据集(来源于NASA数据中心:https://ladsweb.modaps.eosdis.nasa.gov/)中提取得到2010—2017年各灌区分辨率为500 m的年实际蒸散发值。如图1所示,通过对比灌区水量平衡与遥感提取得到的灌区,可发现二者对比整体结果较好,为143.7 mm/a,为18.1%,2可以达到0.631。进一步分析发现,部分干旱半干旱区灌区遥感耗水小于水量平衡计算的灌区耗水。这可能是由于干旱半干旱区作物非生长季大定额的盐分淋洗或保墒灌溉(秋浇、冬灌、春灌)通过水量平衡计算时高估了灌区耗水量。考虑到上述情况,研究中采用灌区遥感耗水年内统计值作为灌区年耗水量。

图1 全国样点灌区2010—2017年MOD16-ET与水量平衡ET的对比结果
1.2 研究方法
Budyko根据流域水量和能量平衡,指出流域蒸散发()同时受降水()和潜在蒸散发(0)2个因素的控制,即Budyko假设,满足的边界条件为:在极端干燥条件下,实际蒸散发将消耗全部供水量;在极端湿润的条件下,潜在蒸散发都将转化为潜热,实际蒸散发为0[2]。
对于灌区而言,在假设年土壤水储量可忽略不计的前提下,水分供给量包括降水量和毛灌溉量,地下水埋深较浅的灌区还存在潜水蒸发gw。本文将供水量(、、gw)之和定义为灌区等效降水量e[16],其中潜水蒸发(gw)采用阿维里扬诺夫公式求得[17]。由于灌区地势相对平整,除灌溉引水及排水外,本文假设水平方向与灌区外水量交换忽略不计。傅抱璞从流域水文气象的物理意义出发,根据微分方程理论给出了符合Budyko假设边界条件的含参数的2种完全等价的解析形式[3]。应用于灌区尺度的傅抱璞公式可以拓展为:
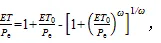
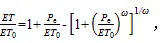
式中:为水热耦合控制参数,反映灌区特征对水量分配的综合影响。如图2所示,Budyko框架应用于灌区时,由于引入灌水量和潜水蒸发量后,等效降水量e增大,减轻了灌区的水分亏缺程度,区域干旱指数0e减小;且由于灌区存在渠道下渗和深层渗漏,实际耗水小于灌区可供水量,灌区蒸散发比e较于同等条件下的自然流域而言往往减小。将Budyko模拟的值和实测值之间的误差值最小化后,即可求得相应参数值。

注自然条件下的等效降水量Pe为实际降水量P。
2 结果与分析
2.1 ET/Pe与ET0/Pe关系分析
为评估引入灌溉水量和潜水蒸发量的Budyko假设在农业灌区上的适用性,首先验证传统仅考虑降水量的Budyko假设能否在灌区适用。如图3所示,仅考虑降水量为灌区可供水量时,蒸散发比和干旱指数0的关系总体上不符合Budyko曲线的变化趋势。其中,在干旱区,>1,这一结果表明干旱区灌区的降水量不能满足灌区作物生产需求,作物生长主要依赖灌溉。对于个别灌区,较小的降水量作为分母导致的比值明显增加。随着湿润程度的增加,半干旱区和半湿润区降水量能够满足作物需水要求的灌区逐渐增加,湿润区降水量已经基本满足灌区作物需水要求,因此基本全部分布在Budyko假设的边界范围内。
如图3所示,将灌溉量和潜水蒸发量引入可供水量后,修正后的蒸散发比e和干旱指数0e表现出减小的趋势,并且均处于Budyko假设的边界范围内。各气候区蒸散发比和干旱指数间均表现出正相关关系,且随着湿润程度的增加,实际蒸散发与0间正相关关系逐渐增强,这与Budyko假设中湿润区主要受到能量限制,干旱区主要受到水量限制的分析相一致。同一气候区内各灌区由于灌排条件、土壤条件、作物种植结构等差异,所表现出的水热平衡关系有所差别,但一般来说在一定范围内波动。
2.2 Budyko假设在灌区耗水估算应用评价
为了验证Budyko假设框架下傅抱璞公式在灌区尺度的适用性,本研究使Budyko曲线估算的灌区年值与灌区遥感值二者误差最小化求得各灌区参数的拟合值,并通过计算各灌区相对误差和均方根误差量化其拟合精度(表2)。结果表明,应用于不同气候条件下的典型灌区时,前文提出的灌区水热关系与Budyko曲线均具有较好的一致性(图4),提出的灌区Budyko框架可以用于分析灌区耗水与潜在蒸散发量及有效水量之间的关系。对于本研究中所涉及的样点灌区而言,估算的逐年误差较小(=9.6~119.3 mm,=1.6%~21.7%),表明使用修正后的傅抱璞公式能够较为合理地对灌区实际蒸散发量进行估算,拟合精度较高。

表2 不同气候区参数ω拟合值及拟合精度统计

图4 不同气候分区内典型灌区的Budyko曲线关系
进一步来看,Budyko曲线在不同气候农业灌区的应用结果有所差别(图5和图6)。Budyko曲线对灌区年估算的相对误差由湿润半湿润区的1.6%~16.0%增加为干旱半干旱区的2.1%~21.7%。从Budyko曲线在区域上应用效果来看,在半湿润区内部,东北地区灌区模拟与遥感之间的相对误差为5.2%,华北地区模拟值与遥感值之间的相对误差则达到8.0%。比较而言,南方灌区植被条件好,尽管由于整体耗水大而引发Budyko曲线对其灌区年耗水估算的绝对误差较大,但Budyko曲线对该区域年度估算精度较其他区域高。
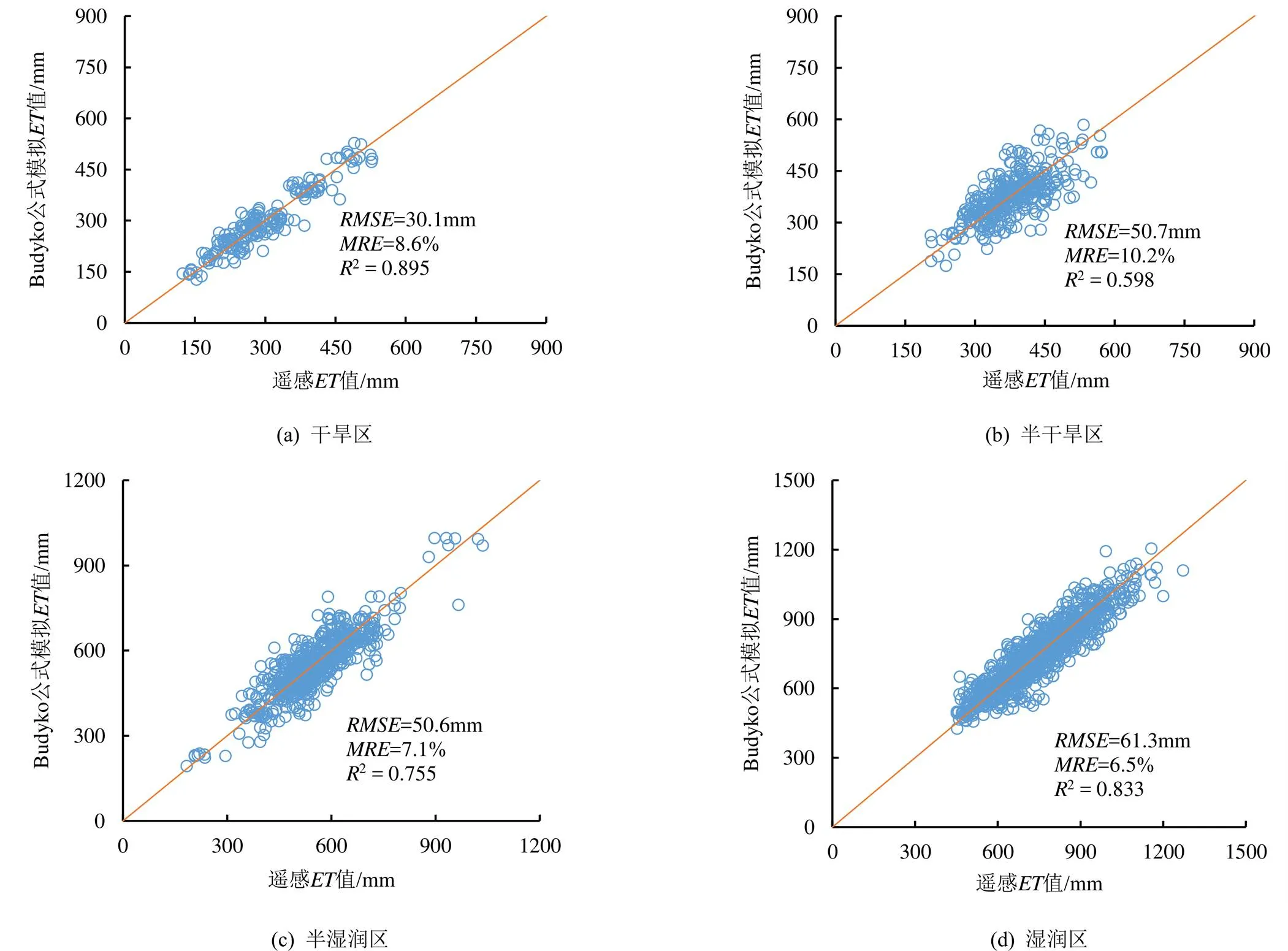
图5 不同气候农业灌区逐年遥感ET与Budyko曲线估算ET的关系
2.3 灌区Budyko公式中参数ω的分布特点
全国灌区Budyko曲线参数在1.12~3.61之间波动(表2),且具有明显的区域分布特征(图7),随着区域湿润程度的增加,参数有所增大。对于所研究的样点灌区来说,参数均值由干旱区的1.28增加为湿润区的2.09。
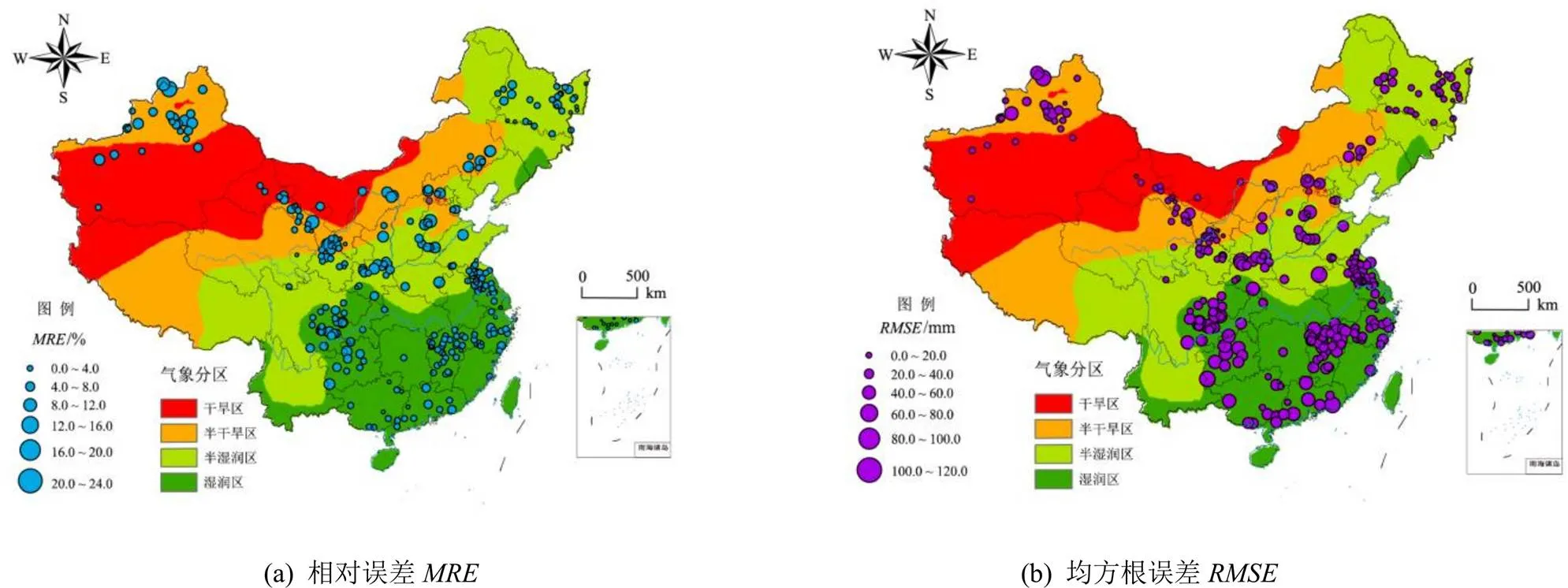
注 (a)、(b)图均基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1569的标准地图制作,底图无修改。

注 (a)图中“×”代表不同气候条件下ω拟合的平均值,“·”代表异常值,横线从上至下分别代表最大值、上四分位值、中值、下四分位值以及最小值;(b)图基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1569的标准地图制作,底图无修改。
3 讨论
Budyko假设下的傅抱璞公式对于不同气候区的灌区拟合精度存在一定的差异,干旱区灌区的拟合精度与湿润区相比较差,这是由于干旱半干旱区在作物非生育期的灌溉量占全年灌溉量的比例相对较大,但该部分灌溉不能够直接影响作物实际蒸散发,同时非生育期的灌溉量难以与气候条件变化同步,因此作物耗水占可供水量的比例与干旱指数的关系在年际间波动较大。同一气候区内部分灌区相对误差较大,可能与灌区在2010—2017年推行节水改造和种植结构改变有关。东北地区和华北地区灌区的拟合精度差异可能同样与当地灌区种植结构改变引起的年际间下垫面变动情况有关:东北灌区以水稻种植为主,种植结构较为单一,下垫面因子在年际间改变不大,而华北地区种植结构较为复杂,下垫面在年际间变动较大。
大量在自然流域中对水热耦合参数的研究表明随着湿润程度增加,水热耦合参数逐渐减小[18-20]。然而,本研究发现随着湿润程度增加,农业灌区Budyko曲线水热耦合参数逐渐增加。这可能是由于受到人类活动影响,灌区处在非稳定的状态[14]。具体而言,干旱半干旱区灌区的参数值与自然流域相比明显减小,这是由于该区域灌溉水中包括的冬春作物非生育期大定额盐分淋洗灌溉与作物耗水没有明显关系[21-23]。值得注意的是,在此种灌溉制度影响下,即使处于极干旱气候条件,灌区实际蒸散发也不能达到水量限制上限(/e=1)。而湿润半湿润区灌区引入灌溉水量后,虽然/e的值有所增加,导致灌区参数减小,但因为降水量已经基本能满足灌区蒸散发要求,灌溉仅起到调节降水和补充作物需水的季节性亏缺的作用,所以影响并不显著。进一步来说,参数是与灌区特征有关的无量纲参数,越大,表示有利于作物耗水的条件越多。通常来说,灌区植被覆盖度越高、土壤蓄水能力越强、节水设施及灌溉管理措施越完善则灌区的参数越大。具体而言,可以通过对灌区植被覆盖度、土壤性质、渠系衬砌率等进行统计,明确参数与上述因素的关系,获得其经验表达式。
在农业灌区应用Budyko曲线时,考虑到95%的灌区都分布在坡度小于5°的平原地带,因此忽略了水平方向水量交换对于灌区耗水的影响。然而对于水网复杂、地势复杂的灌区而言,忽略灌区与周边环境之间的侧向水分交换量,可能会对灌区的可供水量的计算存在一定的影响,继而对灌区水热耦合参数的估算产生影响。此外,因为缺少灌区的具体边界线,因此只能选择灌溉排水发展中心提供的灌区经纬度作为灌区中心构建圆形缓冲区,同时使用了土地利用类型为耕地的遥感数据进行校正,尽量确保提取到的数据为灌区耕地,但是由于灌区上下游实际耗水之间存在一定的差异,因此也会对后续计算产生一定的影响。
总体来说,Budyko假设能够适用于全国不同气候条件下的样点灌区,拓展后的傅抱璞公式对资料不足或无资料农业灌区的年耗水估算等具有潜在的应用价值。值得注意的是,本研究忽略了部分灌区与其外围区域水量的交换所导致的年际之间灌区水储量的变化,会对灌区水热平衡计算引起误差,后续相关研究可通过量化灌区水储量变化来提升Budyko曲线的适用性;同时,农业灌区参数与下垫面因素及灌区设施水平的关系有待于深入研究,以便于进一步扩大Budyko曲线在灌区耗水估算中的应用范围。
4 结论
1)验证了增加灌溉量和潜水蒸发量作为可供水量的Budyko假设条件下的傅抱璞公式在农业灌区的适用性。拓展后的傅抱璞公式能够较好地反映农业灌区的实际蒸散发,估算与实测之间的相对误差均小于21.7%,均方根误差小于119.3 mm。
2)不同气候区农业灌区实测点与Budyko曲线拟合程度有所区别,受到农业种植条件、灌区工程条件、灌溉用水等影响,湿润区和东北地区的拟合精度整体上优于干旱半干旱区,Budyko假设在湿润灌区的应用效果明显好于干旱灌区应用效果。
3)受到非生育期灌水的影响,Budyko假设下傅抱璞公式描述灌区下垫面特征的参数在1.12~3.61之间波动,且随着湿润程度的增加逐渐增大。
[1] DÖLL Petra, SIEBERT Stefan. Global modeling of irrigation water requirements[J]. Water Resources Research, 2002, 38(4): 1-8.
[2] BUDYKO Mikhail Ivanovich. Climate and Life[M]. San Diego, California: Academic, 1974, 508.
[3] 傅抱璞. 论陆面蒸发的计算[J]. 大气科学, 1981(1): 23-31.
FU Baopu. On the calculation of the evaporation from land surface[J],Chinese Journal of Atmospheric Sciences, 1981(1): 23-31.
[4] CHOUDHURY Bhaskar Jyoti. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model[J]. Journal of hydrology (Amsterdam), 1999, 216(1/2): 99-110.
[5] PORPORATO Amilcare, DALY Edoardo, RODRIGUEZ-ITURBE Ignacio. Soil water balance and ecosystem response to climate change[J]. Am Nat, 2004, 164(5): 625-632.
[6] ZHANG Lu, HICKEL Klaus, DAWES Warrick, et al. A rational function approach for estimating mean annual evapotranspiration[J]. Water Resources Research, 2004, 40(2): 1-14.
[7] WANG Xusheng, ZHOU Yangxiao. Shift of annual water balance in the Budyko space for catchments with groundwater-dependent evapotranspiration[J]. Hydrology and Earth System Sciences, 2016, 20(9): 3 673-3 690.
[8] ZHANG Xu, DONG Qianjin, ZHANG Quan, et al. A unified framework of water balance models for monthly, annual, and mean annual timescales[J]. Journal of Hydrology, 2020, 589: 125 186.
[9] HAN Pengfei, ISTANBULLUOGLU Erkan, WAN Li, et al. A New Hydrologic Sensitivity Framework for Unsteady‐State Responses to Climate Change and Its Application to Catchments With Croplands in Illinois[J]. Water Resources Research, 2021, 57(8): 1-28.
[10] 韩松俊, 胡和平, 田富强. 基于水热耦合平衡的塔里木盆地绿洲的年蒸散发[J]. 清华大学学报(自然科学版), 2008, 48(12): 2 070-2 073.
HAN Songjun, HU Heping, TIAN Fuqiang. Annual evapotranspiration in oases of the Tarim basin based on a coupled water-energy balance[J]. Journal of Tsinghua University (Science and Technology), 2008, 48(12): 2 070-2 073.
[11] MILLY Paul Christopher Damian. Climate, soil water storage, and the average annual water balance[J]. Water resources research, 1994, 30(7): 2 143-2 156.
[12] HAN Songjun, HU Heping, YANG Dawen, et al. Irrigation impact on annual water balance of the oases in Tarim Basin, Northwest China[J]. Hydrological Processes, 2011, 25(2): 167-174.
[13] SIMONS Gijs, BASTIAANSSEN Wim, CHEEMA Muhammad Jehanzeb Masud, et al. A novel method to quantify consumed fractions and non-consumptive use of irrigation water: Application to the Indus Basin Irrigation System of Pakistan[J]. Agricultural Water Management, 2020, 236: 106 174.
[14] CHEN Hang, HUO Zailin, ZHANG Lu, et al. New perspective about application of extended Budyko formula in arid irrigation district with shallow groundwater[J]. Journal of Hydrology, 2020, 582: 124 496.
[15] ALLAN Richard G, PEREIRA Luis S, RAES Dirk, et al. Crop evapotranspiration guidelines for computing crop water requirements[R]. Rome: FAO Irrigation and Drainage Paper 56, 1998.
[16] 陈航. 基于Budyko水热耦合平衡理论的灌区耗水对变化环境响应研究[D]. 北京: 中国农业大学, 2020.
CHEN Hang. Study on the response of water consumption to changing environment in irrigation district based on Budyko Hypothesis[D]. Beijing: China Agriculture University, 2020.
[17] 阿维里扬诺夫. 防治灌溉土地盐渍化的水平排水设施[M]. 娄溥礼, 译. 北京: 中国工业出版社, 1963.
AVERYANOV. The level drainage facilities to control the irrigation salinization[M]. Translated by LOU Puli. Beijing: China Industry Press, 1963.
[18] WANG Tingting, SUN Fubao, LIM Wee Ho, et al. The predictability of annual evapotranspiration and runoff in humid and nonhumid catchments over China: Comparison and Quantification[J]. Journal of Hydrometeorology, 2018, 19(3): 533-545.
[19] LI Yangzhong, LIU Changming, YU Wenjun, et al. Response of streamflow to environmental changes: A Budyko-type analysis based on 144 river basins over China[J]. Science of the Total Environment, 2019, 664: 824-833.
[20] 赵香桂, 黄生志, 赵静, 等. 干旱与湿润区流域时变水热耦合参数的归因对比分析[J]. 生态学报, 2021, 24(41): 9 805-9 814.
ZHAO Xianggui, HUANG Shengzhi, ZHAO Jing, et al. Comparative analysis of the attribution of time-varying water-heat coupling parameters in arid and humid basin[J]. Acta Ecologica Sinica, 2021, 24(41): 9 805-9 814.
[21] 郑金丰, 陈永新. 干旱地区发展节水农业与土壤盐碱化防治[J]. 中国农村水利水电, 2000(10): 26-27.
ZHENG Jinfeng, CHEN Yongxin. Development of water-saving agriculture and soil salinization control in arid areas[J]. China Rural Water and Hydropower, 2000(10): 26-27.
[22] 王智慧, 王志慧. 土壤盐碱化防治措施概述[J]. 内蒙古水利, 2016(1): 71-72.
WANG Zhihui, WANG Zhihui. An overview of soil salinization control measures[J]. Inner Mongolia Water Resources, 2016(1): 71-72.
[23] 唐浩瀚. 盐渍化土壤成因分析及修复改良措施探讨: 以甘肃为例[J]. 甘肃科技, 2018, 34(3): 41-42.
TANG Haohan. Analysis of the causes of salinized soils and discussion of restoration and improvement measures: Gansu as an example[J]. Gansu Science and Technoloye, 2018, 34(3): 41-42.
Considering the Budyko’s Assumption to Estimate Evapotranspiration from Irrigation Districts in China
LINYifan1, HUOZailin1*, WANG Chaozi1, ZHANG Chenglong1, HANZhenzhong2, CUIJing2
(1. Collge of Water Resources & Civil Engineering, China Agricultural University, Beijing 100083, China;2. Irrigation and Drainage Development Center, Beijing 100054, China)
【Objective】The Budyko’s assumption is that evapotranspiration is limited by water in semi-arid regions and by energy in wet regions. This paper applied it to estimate evapotranspiration from irrigated agricultural lands in China. 【Method】The results calculated using the Budyko equation were tested against irrigation, precipitation, groundwater evaporation and real evapotranspiration measured from 2010 to 2017 from 282 irrigation districts across China. Based on these data and results, we analyzed the accuracy of the Budyko equation for cropped lands under different climatic conditions. 【Result】The Budyko equation and the Fu's equation, both considering irrigation and groundwater evaporation, are adequate to estimate evapotranspiration from irrigated cropped lands. The mean relative error between the estimatedand the measuredis less than 21.7%. Overall, the estimatedis more accurate for humid areas, where the planting structure and irrigation are less prone to fluctuation and change, than for other areas. Impacted by meteorology, water supply and distribution, soil texture and planting structure in irrigation districts, the parameterin the Budyko curves varies spatially and increases, in general, with humidity. 【Conclusion】The Budyko equation works well for estimating annual evapotranspiration from irrigated cropped lands in China.
Budyko framework; irrigation districts; evapotranspiration; climate
林一凡, 霍再林, 汪超子, 等. Budyko假设在灌区耗水估算的适用性[J]. 灌溉排水学报, 2022, 41(10): 82-89.
LIN Yifan, HUO Zailin, WANG Chaozi, et al. Considering the Budyko’s Assumption to Estimate Evapotranspiration from Irrigation Districts in China[J]. Journal of Irrigation and Drainage, 2022, 41(10): 82-89.
S271
A
10.13522/j.cnki.ggps.2022162
1672 - 3317(2022)10 - 0082 - 08
2022-03-28
国家自然科学基金重点项目(52130902)
林一凡(1997-),女。硕士研究生,主要从事灌区耗水规律研究。E-mail: linyifan1997@126.com
霍再林(1977-),男。教授,博士,主要从事水文水资源及农业高效用水的研究。E-mail: huozl@cau.edu.cn
责任编辑:赵宇龙
