基于本地差分隐私的K-modes聚类数据隐私保护方法

张少波，原刘杰，毛新军，朱更明

（1.湖南科技大学计算机科学与工程学院，湖南湘潭 411201；2.国防科技大学复杂系统软件工程重点实验室，湖南长沙 410073）

1 引言

聚类是一种常用的数据挖掘方法，它按照某种特定标准将数据集分割为不同的簇，使得同一个簇中数据相似性较高［1］.K-means是聚类中的经典算法，其实现简单且聚类高效，它只适用于处理数值型数据集，而对分类型数据的聚类通常使用K-modes算法［2，3］.目前，聚类分析在数据分析、服务推荐等多个领域发挥着重要的作用，但聚类数据中通常包含大量的个人敏感信息，如对客户数据进行聚类分析可为不同类型的客户提供个性化服务，但攻击者从这些信息中能推测出用户的兴趣爱好［4～6］.因此在使用聚类对用户数据分析过程中，迫切需要保护用户的个人隐私.

差分隐私［7］是采用严格数学定义的隐私保护模型，它可以量化用户隐私保护程度，并且能抵御攻击者发起的背景知识攻击和合成攻击［8，9］.目前差分隐私已广泛应用于数据挖掘、数据发布、位置服务等领域的隐私保护［10～12］，而且它与随机扰动、数据交换等隐私保护技术相比［13，14］，在聚类分析数据隐私保护方面具有明显的优势［15～17］.差分隐私具有强健的隐私保护能力，但它需要一个可信第三方对数据进行处理，而由第三方造成的数据泄露事件却层出不穷，如谷歌，雅虎和微软等公司的数据意外泄漏事件，这不仅造成了用户隐私信息的泄露，还严重损害了公司声誉.因此，现实中很难找到完全可信的第三方.针对该问题，本地差分隐私（Local Different Privacy，LDP）在保证数据可用性的前提下，通过在用户端对数据进行扰动，实现了对用户隐私的去第三方保护，并且它与差分隐私同样采用了严格数学定义的隐私保护模型［18］，因此它已成为隐私保护领域中解决此类问题的重要方法.

目前，国内外学者已提出一些本地差分隐私算法，其中RAPPOR算法是频数统计的经典算法［19］，它误差小，数据可用性高，但它需要候选属性值已知.针对RAPPOR的不足，文献［20］在其基础上对字符串进行映射，实现了无需候选属性值已知的频数统计.针对集值数据的频繁项查询问题，文献［21］提出了包含两阶段机制的LDPMiner算法，文献［22］在其基础上进一步研究，提出了具有更高查询精度的SVIM（Set-Value Item Mining）算法.不同于频率估计方法，文献［23］通过数据离散化操作实现了在［-1，1］区间中的均值估计，然而该方法的输出结果是两个固定值，这会导致估计值偏离［-1，1］区间.针对该问题，文献［24］将［-1，1］区间中的任意值扰动到受约束区间［-C，C］，然后在此区间内计算该扰动值的边界.此外，本地差分隐私在空间范围查询，众包数据收集等领域也得到了广泛应用［25，26］.虽然本地差分隐私可以有效应对第三方隐私泄露问题，但将它应用于聚类分析数据隐私保护时，仍然存在如下挑战：（1）如何降低噪声在聚类更新质心过程中的影响.如果直接根据收集到的扰动数据对用户进行分簇，然后再基于扰动数据计算每个簇的质心，则会进一步放大噪声的影响.（2）如何以较小的噪声误差和通讯开销完成聚类.如果用户将自身所有数据扰动并汇报，则所需的通讯开销以及聚类结果的噪声误差会较大.针对上述挑战，本文提出一种基于本地差分隐私的K-modes聚类数据隐私保护方法（Local Different Privacy K-modes，LDPK）.该方法首先对数据随机采样，然后采用本地差分隐私技术在用户端对采样数据进行扰动，最后通过服务端与用户端的交互迭代完成聚类.本文主要贡献如下：

（1）构建了一个基于本地差分隐私的K-modes聚类数据隐私保护框架.引入本地差分隐私技术在用户端对数据进行扰动，并通过服务端与用户端的交互迭代，实现了对聚类过程中用户数据的去第三方隐私保护.

（2）为提高聚类结果的质量并降低通讯开销，在使用本地差分隐私技术扰动前，对数据进行随机采样，避免因隐私预算分割导致的聚类质量降低以及发送全部数据带来的通讯开销较高问题.

（3）理论分析证明了方法的隐私性和可用性，真实数据集上的实验结果表明，该方法在满足本地差分隐私机制的前提下，有效保证了聚类结果质量.

2 本地差分隐私与K-modes聚类

2.1 本地差分隐私

针对第三方存在泄露用户隐私的风险，本地差分隐私直接在用户端对数据进行扰动，它能满足用户对个人隐私保护的更高要求.本地差分隐私的形式化定义如下：

定义1假设n名用户都至少拥有一条记录，其隐私保护算法为M、定义域为Dom、值域为Rnm.如果任意两条记录t(t∈Dom)和t'(t'∈Dom)，经M处理后得到相同输出结果t*(t*∈Rnm)的概率满足式（1），则M满足ε-LDP.

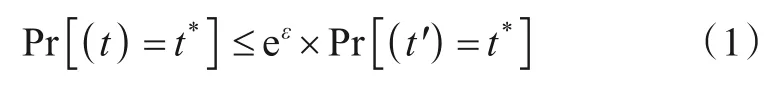
定义1中的ε是隐私预算，其值大于0.它表示用户数据的隐私保护强度，ε越小，隐私保护程度越高，但相应的数据可用性就会降低，因此在具体应用中要从多个角度权衡ε的取值.同时从定义1可看出，本地差分隐私通过控制任意两条记录输出结果的相似性来保护数据隐私.经过本地差分隐私处理后，从输出结果逆推出输入数据是非常困难的.

2.2 K-modes聚类

K-modes算法由K-means扩展而来，主要应用于分类型数据的聚类.它采用Hamming距离衡量两个点之间的间距［27］，并通过计算属性值的众数来确定簇的质心.K-modes算法的具体步骤如下.

步骤1：确定需要划分的簇数k，从数据集中随机选择k个点作为起始质心.

步骤2：分别计算数据集中每个点与每个质心的距离，并将点划分给距离最近的质心.

步骤3：得到k个簇后，通过计算各个属性值的众数，然后确定每个簇的新质心.

步骤4：重复步骤2和步骤3，直到相邻两次的聚类结果不再发生变化.

3 K-modes聚类数据隐私保护方法

3.1 问题描述

假设存在用户集U={u1，u2，…，}un和属性集M={A1，A2，…，Ad}.每个用户ui(1≤i≤n)都拥有一个d维属性元组mi={a1，a2，…，ad}，aj(1≤j≤d)是Aj的某个属性值.K-modes算法的目标是将用户划分为k个簇C={c1，c2，…，}ck.在分簇过程中通常包含一些用户敏感信息，而采用可信第三方对聚类数据进行隐私保护的方法，却很难找到绝对可信的第三方来防止用户隐私数据泄露.表1为本文中使用的重要符号.

表1 符号说明

3.2 具体实现方案

本文提出了一种基于本地差分隐私的K-modes聚类数据隐私保护方法，其整体框架如图1所示.用户ui向服务端发送数据时，为避免隐私预算分割并降低通讯开销，先对数据进行随机采样，然后采用本地差分隐私算法对采样数据进行扰动，最后将得到的扰动数据发送给服务端.

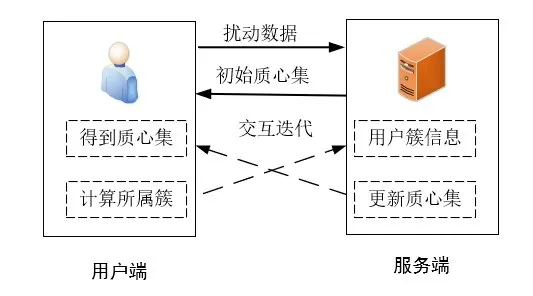
图1 基于LDP的K-modes聚类框架

上述过程无需第三方对数据进行隐私预处理，确保了用户的隐私不受不可信第三方的威胁.服务端在收集到所有用户的扰动数据后，依据属性集信息确定初始质心集V={ν1，ν2，…，νk}，并将其发送给所有用户.用户ui从服务端接收到质心集后，根据自身真实数据mi计算出距离最近的质心νy(1≤y≤k)，然后依据质心νy确定所属的簇cy并汇报.服务端收到用户的簇信息后，结合扰动数据求解新的质心集.最后重复上述的交互过程不断进行迭代，直到各个簇中的质心在相邻两次迭代中不再发生变化.

3.3 用户端数据处理

用户端的每个用户ui都拥有一个真实数据集mi={a1，a2，…，}ad，LDPK采用目前本地差分隐私技术中高精度的最优一元编码算法［28］对其进行扰动.该算法在扰动前要对数据进行编码，以a1为例，设它对应的属性A1为“民族”，则属性域大小|A1|为56，用一个长度为56的比特字符串b={0，0，…，0}表示该属性域.每个民族对应b中一个比特位，设a1为汉族，而汉族对应第x个比特位，故将第x个比特位设为1，得到比特字符串b={0，…，1，0}.对mi中每个属性值aj都按照上述过程编码，以x表示属性值对应的比特位，以w(1≤w≤|bj|)表示x的取值范围，编码如式（2）所示：

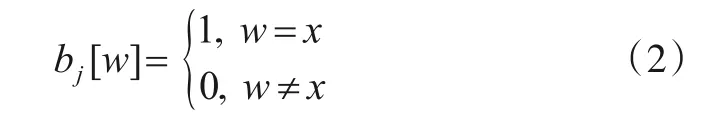
编码完成后得到比特字符串Bi={b1，b2，…，bj，…，bd}，然后对Bi进行随机采样，并对采样值bj采用式（3）进行扰动.

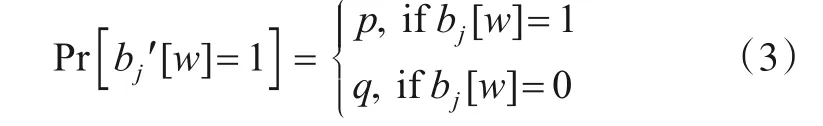
算法1数据扰动输入:用户ui的数据mi={a1，a2，…，}ad,隐私预算ε;输出:扰动后的值(j，bj');1. 将mi={a1，a2，…，}ad编码为Bi={b1，b2，…，bd};2. 从Bi中随机采样bj,同时设置b'j={0，0，…，0},|b'j|=|bj|;3. FOR w=0 to|bj|-1 do 4. IF bj[w]=1 5. Pr[bj'[w]=1]=1/2 6. IF bj[w]=0 7. Pr[bj'[w]=1]=1 eε+1 8. Return(j，bj')

在之后的迭代过程中，服务端先计算出质心集合V={ν1，ν2，…，νk}，并发送给所有用户.然后每个用户ui根据自身的真实数据mi计算出距离最近的质心νy.最后再依据质心νy确定所属的簇cy，并将其汇报给服务端.

3.4 服务端求解质心

服务端从所有用户收集到扰动数据B'={b1'，b2'，…，bd'}后，首先从属性集中随机选取k个d维属性元组作为初始质心发送给用户，然后依据扰动数据和用户返回的簇信息计算出新的质心集V={ν1，ν2，…，νk}.其具体步骤如下：

（1）根据每个用户汇报的cy，将所有用户划分为k个簇C={c1，c2，…，ck}.|cr|(1≤r≤k)表示簇中的用户人数，因用户对数据进行了采样，故簇中每个属性对应的用户人数变为|cr|d.为便于计算，后续以|cr|'表示|cr|d.

（2）计算每个簇中各个属性值的频率.以簇cr中的属性Aj为例，统计对应扰动数据b'j的每个比特位得到S={s1，s2，…，sl}，sl(0≤l＜|b'j|)表示b'j中第l个比特位为1的个数，再结合其他数据计算出Aj每个属性值的估计频率t'.

（3）服务端在计算出各个簇中所有属性值的频率后，选取每个属性中频率最高的属性值，以它们的集合作为该簇的质心，最终得到新的质心集V={ν1，ν2，…，νk}.服务端质心求解的具体过程如算法2所示.

算法2计算迭代质心输入:用户簇C={c1，c2，…，}ck,每个簇的数据B'={b1'，b2'，…，bd'},p,q;输出:新的质心集合V={ν1，ν2，…，}νk;1. FOR C from r=1 to k do 2. From b1'to bd'do 3. 统计每个比特位得到S={s1，s2，…，sl}4. FOR i=0 to l-1 do 5. t'i=si-|cr|'×q|cr|'×( )p-q 6. Return a=Max(t')对应的属性值7. Return νr={a1，a2，…，ad}8. Return V={ν1，ν2，…，}νk

服务端最后向用户发送新的质心集，并根据从用户收集到的簇信息不断重复上述过程，直到各个簇中的质心在相邻两次迭代中不再发生变化.

3.5 隐私性和可用性分析

本文提出的LDPK方法中只有算法1需要隐私预算，因此只要算法1满足本地差分隐私的定义，则LDPK方法同样满足该定义.

引理1算法1满足本地差分隐私的定义.

证明设存在属性Aj的两个属性值x1和x2，由它们的扰动结果bj'可得：

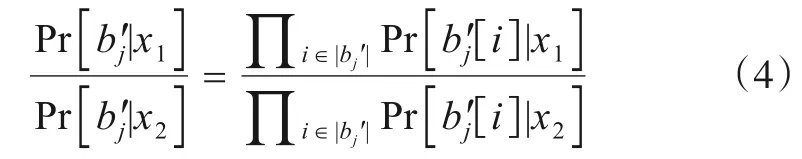
因bj'中每个比特位都是独立扰动，故式（4）只在x1和x2处不同，可以得出：

对于式（5），当bj'中的x1位置为1，x2位置为0时，它右侧的比值达到最大：

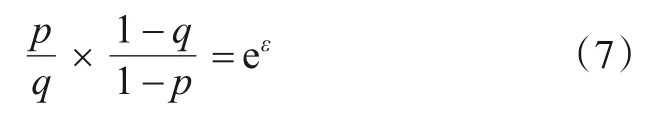
因此，算法1满足本地差分隐私的定义.

服务端在更新质心时，由于没有收集用户的真实数据，它不能计算出每个属性值的真实频率t，只能得出估计频率t'.为了降低噪声的影响，我们希望计算出的t'满足无偏性.因此，需要通过如算法2的步骤5所示来计算t'.

引理2通过算法2的步骤5计算出的估计频率t'满足无偏性.

证明假设t与t'分别为簇cr中某属性值a的真实频率与估计频率，g与g'分别为a的真实频数和估计频数.设a'为a对应的比特位，s是扰动数据中a'为1的个数.

由于服务端无法获得a的真实频数g，为了求解t'，需要计算估计频数g'.因用户以两种概率对每个比特位进行响应，故|cr|'个用户对a'的响应结果构成了满足二项分布的|cr|'个0/1序列.根据该二项分布，构造相应的似然函数：

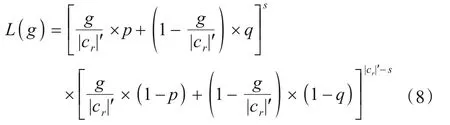
对式（8）两侧取对数并对g求导即可求出它的极大似然估计g'：

对于求解出的g'可以证明其满足无偏性：

因g'满足无偏性，故可求出无偏估计频率t'：

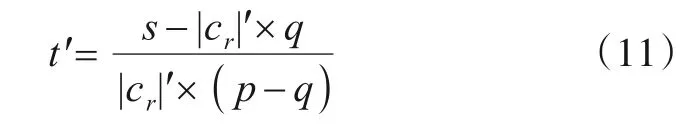
对用户数据直接扰动存在的聚类质量降低和通讯开销较高问题，LDPK方法通过对数据采样，使用户在发送扰动数据时只需发送采样值，大大降低了通讯开销.但为了降低扰动数据中噪声的影响，需要较大的数据量，而采样使任意属性值对应的用户总数变为实际值的1/d，因此需要对采用这两种方式得到的扰动数据的可用性进行分析.

引理3对用户数据采样相比于分割隐私预算可以提高扰动数据的可用性.

证明设有n名用户的数据是d维属性元组，隐私预算为ε，其某个属性值的估计频数为g'，f为它对应的比特位，s是扰动数据中f为1的个数，真实频率为t.若不采样且该属性值获得全部ε，则由式（9）可得g'的方差为：

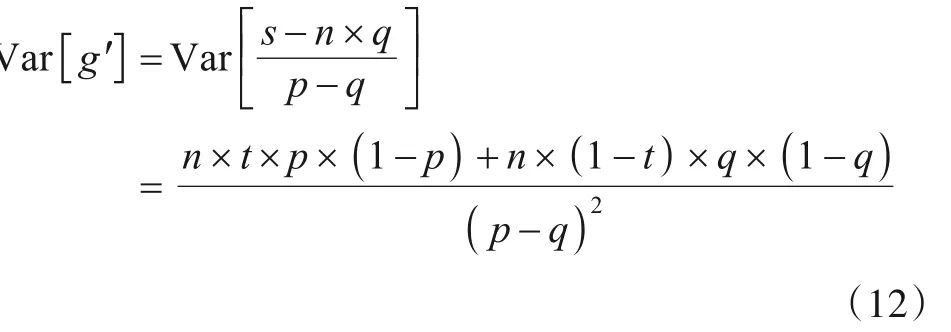
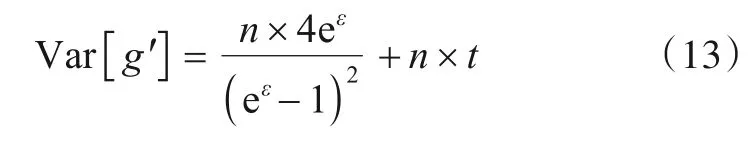
式（13）中n×t为属性值的真实频数，它是一个常数，为了便于计算将其省略.同时又因两种方法中属性值对应的用户数目不同，导致无法直接比较它们的方差，故对式（13）进行如下转换：

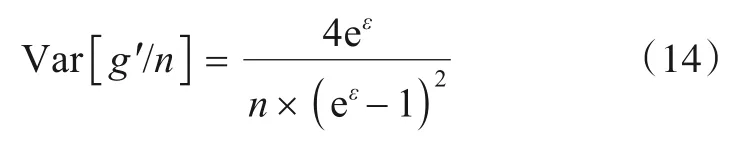
对d维属性随机采样使得属性值对应的用户数变为n/d，其方差以η1表示：

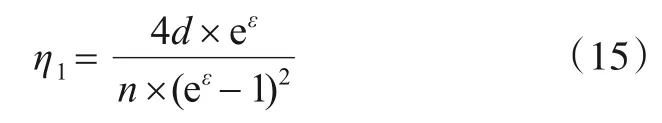
对隐私预算分割使得每个属性获得的隐私预算变为ε/d，其方差以η2表示：

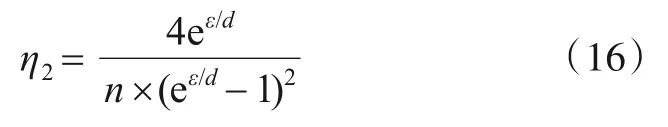
如果采用随机采样得到的扰动数据可用性优于隐私预算分割，那么η2和η1应当满足η1＜η2，而它们之间的大小关系如下：

由上文可知隐私预算大于0.因此，对于式（17）结果的左侧部分可以得出：

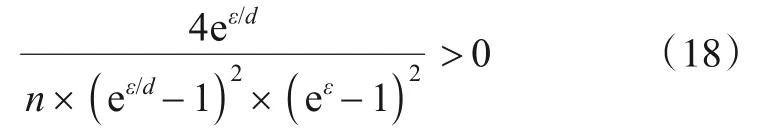
定义y=eε/d，将它代入式（17）的结果部分.同时又因式（18）大于0，故将式（17）结果的左侧部分舍去以简化运算，则式（17）可化简为：

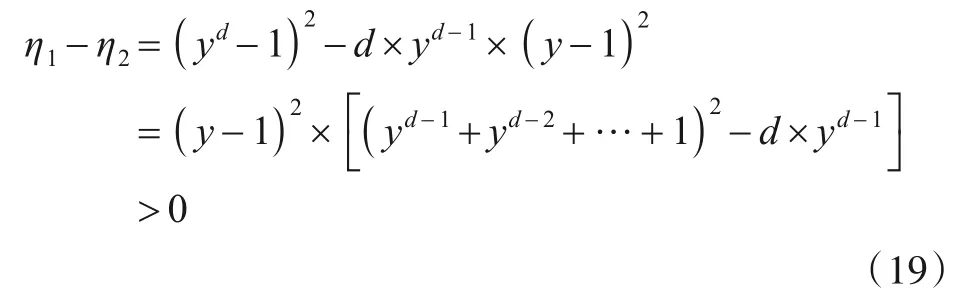
由式（19）可知η1＜η2，因此对用户数据随机采样相比于分割隐私预算，可以提高扰动数据可用性.

4 实验结果分析

实验主要采用两个真实数据集，一个数据集来自IPUMS网站的公开数据，从中选取了USA的5万条普查数据，如表2所示，每条记录包含5个分类属性.另一个是隐私保护研究领域常用的UCI数据库中Adult数据集，经过删除其中的无效记录后共有30162条记录，如表3所示，每条记录分别选取6个分类属性.

表2 USA普查数据集属性

表3 Adult数据集属性

实验的硬件环境为：Intel（R）Core（TM）i5-7300HQ CPU@2.50 GHz 2.50 GHz，8.00 GB内存.软件环境为：Microsoft Windows 10.采用PyCharm开发平台，以Python编程语言实现.

实验采用准确率AC（Accuracy）和熵E（Entropy）作为聚类质量评价指标，以无隐私保护下的K-modes聚类结果作为真实值.评价指标如式（20）和式（21）所示：

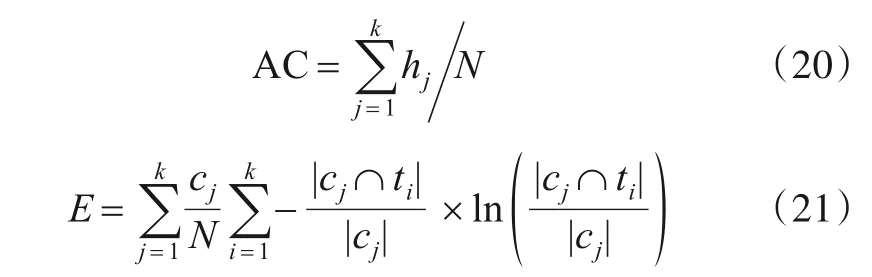
其中k是聚类簇数，hj是采用隐私保护算法得到的聚类簇中正确聚类的数据个数，N是数据集的大小，ti是无隐私保护下得到的聚类簇，cj是采用隐私保护算法得到的聚类簇.实验研究相关参数对LDPK算法性能的影响并与现有差分隐私保护下的K-modes算法［17］（Different Privacy K-modes，DPK）进行对比.聚类簇数k取3，同时为了降低初始质心选择和扰动数据中噪声对结果的影响，每个实验进行300次，结果取平均值.

4.1 参数变化对LDPK性能的影响

改变隐私预算ε，其他参数保持不变，分析隐私预算大小对LDPK性能的影响.由图2可知随着ε的增大，聚类结果的准确率随之提升，熵随之降低，其原因在于扰动数据中的噪声添加量取决于ε的值.ε越小，扰动数据中添加的噪声越多，则聚类结果质量越低.ε越大，扰动数据中添加的噪声越少，则聚类结果质量越高.

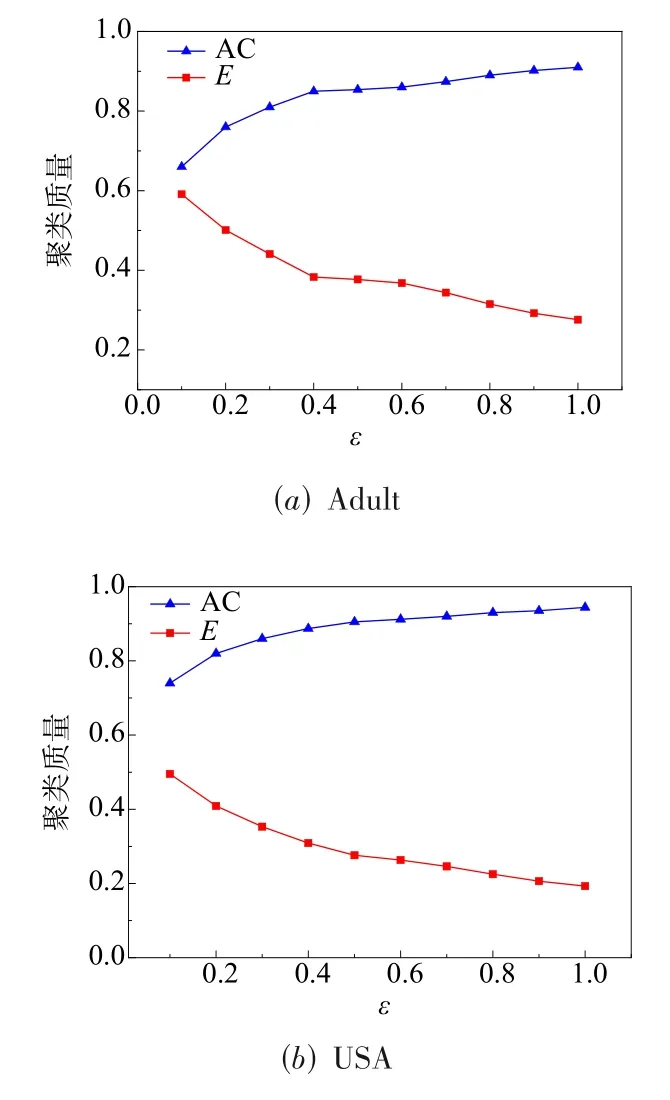
图2 隐私预算ε对算法性能的影响

将隐私预算ε设置为1.0，其他参数保持不变.从数据集中随机抽取不同数目的记录，分析数据集大小N对LDPK性能的影响.由表4和表5可知随着数据集的增大，聚类结果的准确率随之增加，熵随之降低，其原因在于本地差分隐私中每个用户以一定的概率汇报真实值，而根据大数定理，同等条件下实验重复次数越多，随机事件的结果越接近其真实频率.因此数据量越大，响应随机性的影响越小，聚类结果的质量也就越高.

表4 Adult大小对AC和E的影响

表5 USA大小对AC和E影响

4.2 算法性能对比

改变隐私预算ε，其他参数保持不变，对比LDPK与DPK的聚类结果质量.由图3可知，DPK的聚类结果质量略优于LDPK，其原因在于DPK依靠第三方对真实数据进行隐私处理，可以更好的控制噪声添加，所以聚类结果的质量较高.但LDPK的聚类结果质量与DPK相比差距不大，这表明通过对用户数据的随机采样以及服务端与用户端的交互迭代，LDPK有效保证了聚类结果的质量.同时与DPK相比，LDPK不需要任何第三方对真实数据进行隐私预处理，避免了第三方泄露用户隐私的风险，提高了用户数据隐私的保护程度.

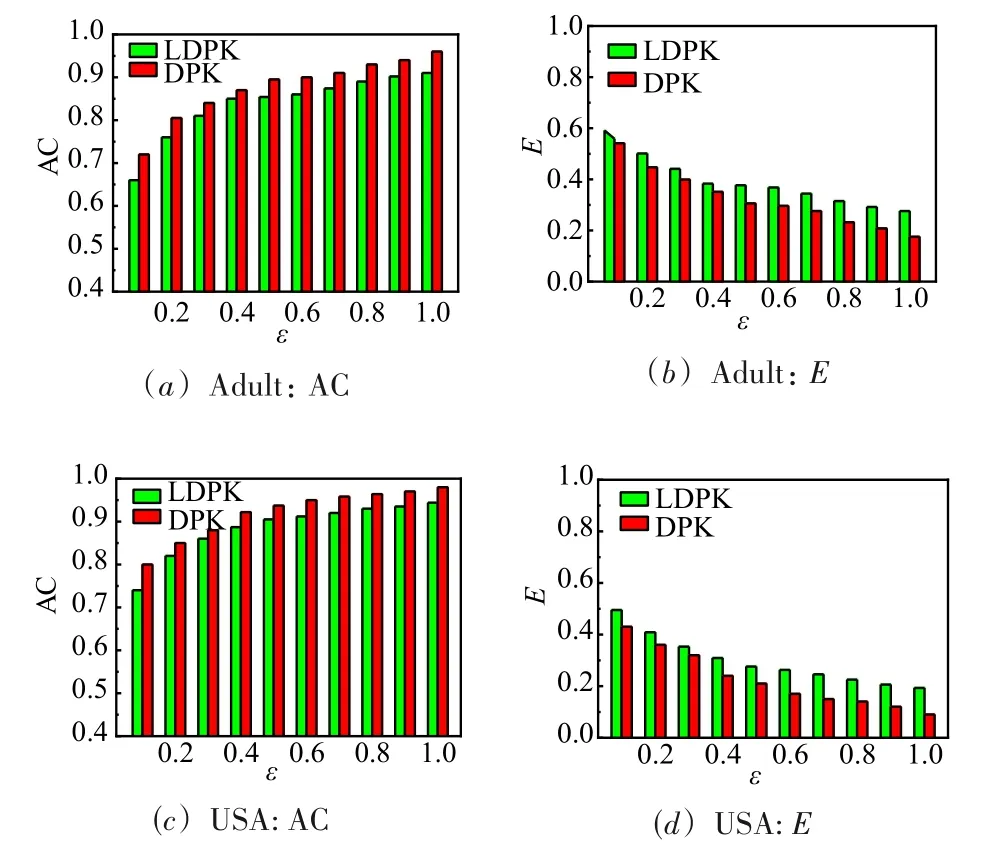
图3 性能对比

5 结语

针对K-modes聚类数据中用户敏感信息的隐私保护问题，当前主要依靠基于可信第三方的隐私保护方法，但实际应用中该第三方也存在隐私泄露风险.本文提出了一种本地差分隐私下的K-modes聚类数据隐私保护方法.该方法结合本地差分隐私和随机采样技术在用户端对数据进行扰动，使得整个聚类过程中服务端都无法获得用户的真实信息，同时它基于去第三方思想，避免了第三方泄露用户隐私的风险.在真实数据集上的实验结果表明，该方法在满足本地差分隐私机制的前提下，有效保证了聚类结果的质量.

本文提出的方法使用户所有数据受到同等程度的隐私保护，但有些数据不需要很强的隐私保护度.因此在未来工作中，我们将尝试对用户数据敏感度分级，允许服务端直接收集敏感度较低的数据，而对敏感度较高的数据采用本地差分隐私进行保护，以满足用户对不同敏感度数据的个性化隐私保护需求.