军用装备滚装船配载问题研究*

齐玉东 宋 冰

（海军航空大学 烟台 264001）

关键字 军用装备；滚装船；配载

1 引言

为应对国家安全威胁，必须做好两栖登陆作战准备。两栖登陆作战中海上投送是作战的初始阶段和首要环节，而装载方案的好坏将直接影响到海上投送的速度、安全及成本。传统的船舶装载方案由人工编制，主要依赖于经验和基本原则。急需对装载问题进行较为系统的研究，利用信息化技术，研究科学可行的配载方案，以提高方案编制的效率。

滚装船是最适应部队实施海上输送的船型，由于其实现了装备车辆在水平方向的滚动开进，能够快速提高部队的装载卸载速度［1］。除部分海军制式登陆舰船外，某些民用大型滚装船也具有较强的装载能力。例如军民两用大型滚装船“渤海翠珠”号，排水量达3.6万吨，可装载大小车辆300余辆［2］。据了解，我国大中型民用滚装船的数量较为可观，在战时若以军用登陆舰船为骨干，民用滚装船为重要补充，充分发挥民船的“第二海军”作用，则可迅速提高我海上投送能力，具有重要的现实意义。

当前，国内外学者对军事装备在民用滚装船上装载的研究还不多。文献［3］通过分析装载的主要流程，设计了一种借助线性规划求解的船运装配载系统。文献［4］研究滚装船的装载特点，建立了综合考量船舶安全性、装载速度以及成本收入情况的多目标模型，并使用贪婪算法对问题进行仿真解算。文献［5］提出了可以对船舶装配载方案计划进行效能评分的优化算法，并利用该算法实现了对装配载计划的选择打分。文献［6］讨论了军事重装备在民用船舶上装载的可行性。因此，本文以军用装备在民用滚装船上的装载为研究内容，提出了相关配载的模型和算法。

2 配载问题描述与分析

本文所述的配载问题可以描述为：给定一系列需要装载的军用车辆以及可供装载的民用滚装船，通过合理安排军用重型车辆的数量和位置，在保证最大载重量和船只稳性安全的前提下，使得船舱甲板利用率、所装载装备价值最大化。根据滚装船的相关资料和文献，确定问题的相关数据和约束条件［7］。

2.1 车辆舱及载车线

通常多层的滚装船的船舱内都会拥有较大的装载空间，每个船舱的地面都是划分清晰的一条条车道，也称载车线，车辆在车道线上依次排开进而实施装载。车道线通常在附近预设底座、地铃等设备用于车辆或者货物的捆绑加固，防止车辆装备在海上航行中发生位移造成事故。因此，在配载时可以将载车线的长度作为主要的影响因素，装备的配载转换为求解装备位于具体哪条载车线上和在载车线上的具体位置。如图1所示。

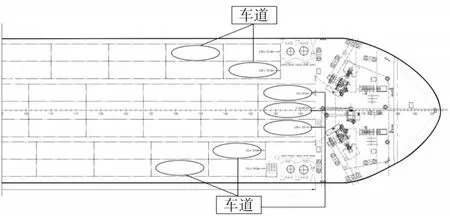
图1 “渤海珍珠”号客滚船主甲板车道布置示意图

2.2 军用装备

滚装船上所装载的军用装备主要包括坦克、步战车、自行火炮、运输车等，在具体配载时可以简化为大小不等的矩形。

2.3 车辆间距要求

为保证车辆装载安全，装备间还应保持一定间距，根据相关技术标准，轮式装备前后距离应不少于1.2m，左右间隔不少于0.5m。履带装备及自行火炮前后距离应不少于1.5m，左右间隔不少于0.5m。一是防止航行过程中装备发生位移产生碰撞，二是确保有足够的空间进行装备捆绑加固［8］。

2.4 船舶载重和稳性要求

为保证船舶海上输送的安全，需重点关注以下三个方面的装载状态：一是载重量要求。所有装载车辆装备的质量之和不得超过船舶的装载能力。二是船舶的稳性要求。船舶在横倾状态下，横向的水压以及装载货物会产生较大的横向力矩，从而引起船舶横向倾斜。因此在计划方案时，车辆应当左右和前后尽量均衡分布，在方案制定完成后还要进行数据验算，保证船舶的稳定性和强度满足设计要求。三是甲板强度要求。由于军事装备的重量较大，要提前计算甲板强度是否能满足装备的装载要求。

2.5 装备数量限制

在具体的装载实践中，每种装备的数量并不是无限的，一般来说会有最大数量限制。具体情况需要结合实际进行分析。

3 配载数学模型

3.1 变量定义

首先将模型中涉及的符合进行定义和说明。

表1 变量说明

3.2 考虑船舱的最大利用率

这种情况是在敌情威胁不大时，根据任务需要，确定某种船型后只考虑船舱的最大利用率，也就是要求装载尽可能多的装备，使得总载车线的利用率以及载重利用率最大。

定义船舱载车线利用率函数：

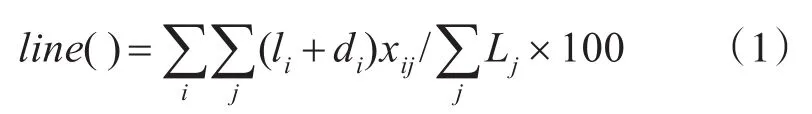
定义船舱载重量利用率函数：

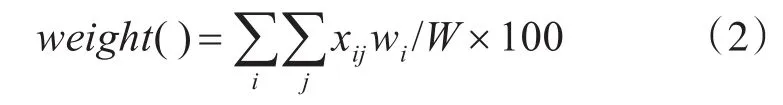
通过多目标规划的加权系数法［9］，目标函数可以表示为

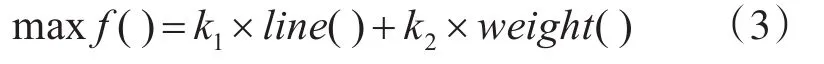
其中k1，k2为权重因子，通常根据具体情况由经验确定，其权重之和为1，目标函数值越大越好［10］。

约束条件为

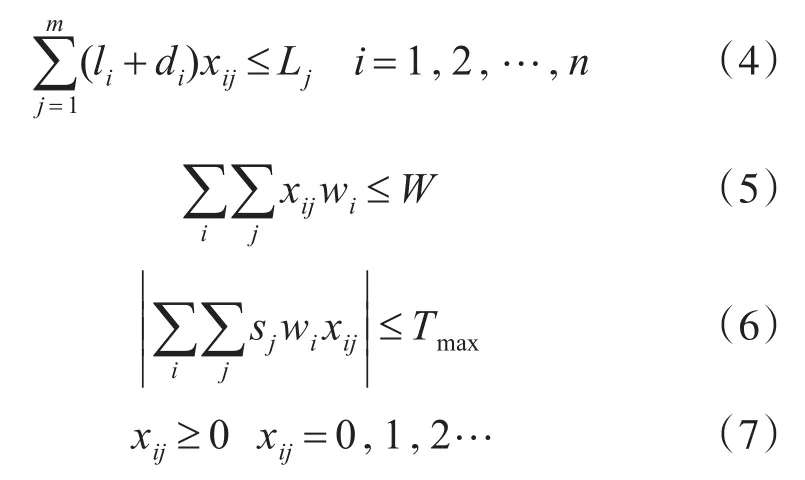
式（4）为载车线长度约束，表示每条载车线上各种车型的长度加上车间隔之和不能超过该条载车线总长度；式（5）为质量约束，表示装备总质量不能超过船舱最大载重；式（6）是横倾力矩约束，表示各型装备的总横倾力矩不能超过船舱的最大横倾力矩；式（7）表示载车线上装备的数量是不小于0的整数。

3.3 考虑所装载装备的战斗力价值因素

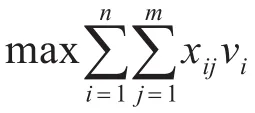
4 配载算法

本文所涉及的配载问题需要解决两个问题：一是确定装载装备的类型、数量；二是确定装备在船上的具体位置。该问题也是一种组合优化问题，是在特定的空间范围内得到满足最优目标函数的分布方式，由于组合优化问题是NP难问题，在大规模问题中全局最优解较难取得，通常使用优化算法求得近似最优解。常用的包括模拟退火算法、遗传算法、蚁群算法等［11］。本文采用遗传算法求解该问题，算法流程图如图2所示。

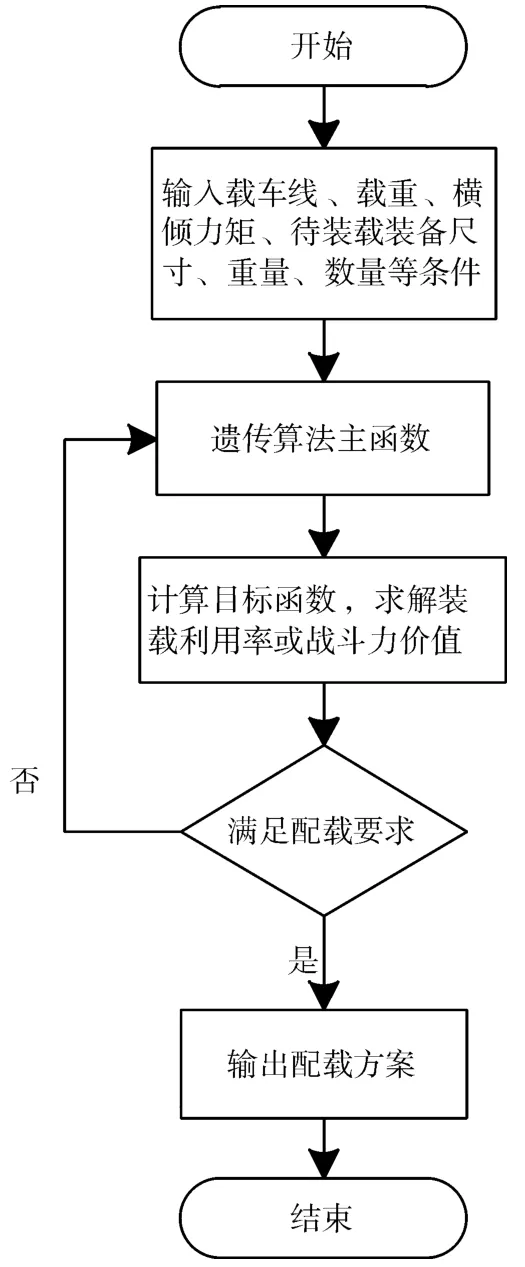
图2 算法流程图

5 实例分析

某部现有一批待运装备，计划运用某型客滚船进行运输。船舱共有3条载车线，长度分别为90，105，85m，最大载重1000t，最大横倾力矩1000kN·m。本文设定装备间距为0.75m，装备的具体参数见表2。

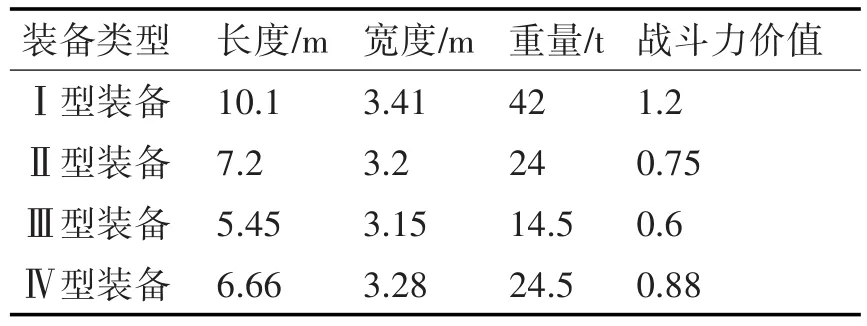
表2 装备部分参数

5.1 考虑船舱的最大利用率

假设每种待装载装备的数量没有限制，权重系数k1为0.8，k2为0.2。使用遗传算法仿真，相关参数的制定对算法的结果将产生较大影响，为获得最佳参数组合，通常需要多次实验才能得到最佳参数［12］。本文参数设置为初始种群大小为200，交叉概率为0.8，变异概率为0.2，迭代次数为300，在Matlab中求解得出优化的配载方案为Ⅰ型装备18辆、Ⅱ型装备7辆、Ⅲ型装备1辆、Ⅳ型装备3辆、载车线使用率99.78%、载重量利用率84.33%，满足配载需求，实验结果见表3。

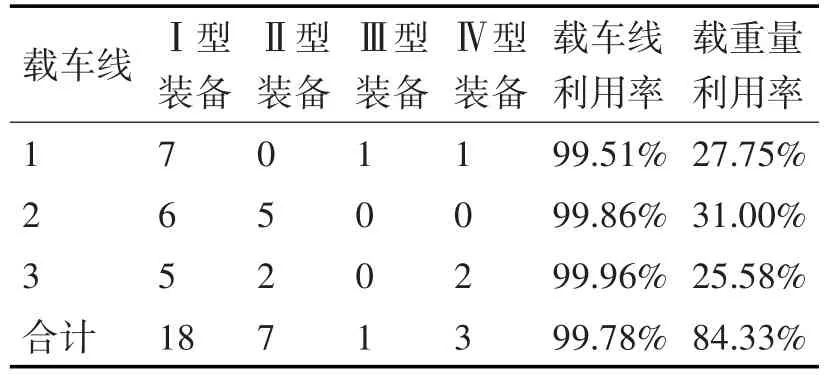
表3 仿真实验结果

5.2 考虑所装载装备的战斗力价值因素

情况一：每种装备的数量没有限制。

在Matlab中使用遗传算法求解得出优化的配载方案为Ⅰ型装备0辆、Ⅱ型装备0辆、Ⅲ型装备1辆、Ⅳ型装备36辆。结果见表4。

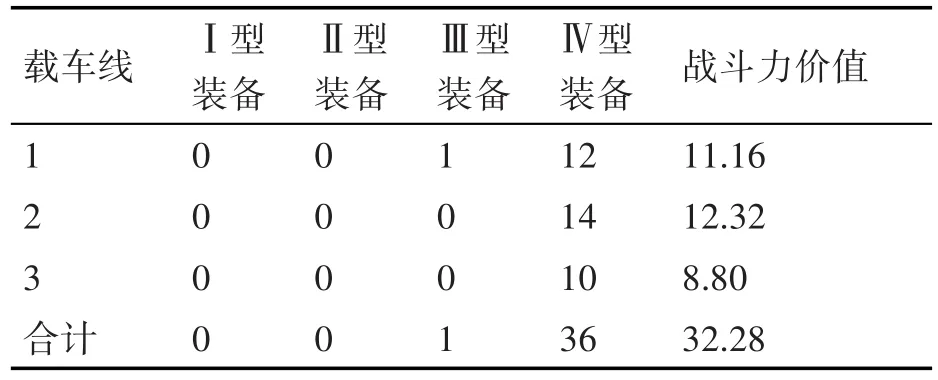
表4 情况1计算结果

根据计算结果，可以看出在战斗力价值影响下，由于每种装备数量不受限制，算法优先安排单位长度价值最高的Ⅳ型装备进行配载。

情况二：装备的数量有限制。

假设Ⅰ装备至Ⅳ装备最多分别装载15、20、20、15辆。增加条件约束后在Matlab中使用遗传算法求解得出优化的配载方案为Ⅰ型装备15辆、Ⅱ型装备0辆、Ⅲ型装备2辆、Ⅳ型装备14辆。结果见表5。

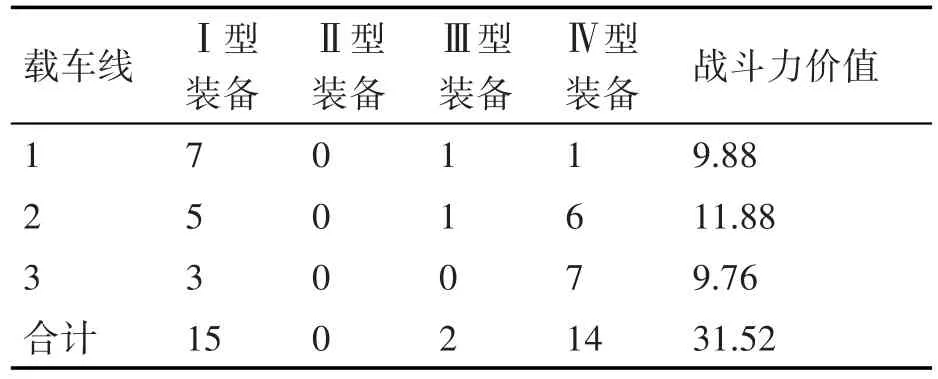
表5 情况2计算结果

综上，该模型和算法可以实现较为准确的实现配载安排，实际装载时，可根据计算结果，按照每条载车线上每种装备数量依次装载即可满足要求。

6 结语

军事装备的船舶配载是海上投送中的一项重要工作。本文通过分析军用装备在民用滚装船上的装载的基本要求，提出了相关配载的模型，并利用遗传算法求解结果。实验表明，该方法对提高部队船舶配载方案的编制效率、提升运输安全具有指导意义。但本文研究的算法还不够深入，对算法效率的优化改进是下步研究的主要方向。