输电线路工程三绳索吊升张力控制技术研究
2022-11-08周威宋泽明胡春华何成郝玉靖
周威,宋泽明,胡春华,何成,郝玉靖
(1.中国电力科学研究院有限公司,北京 100192;2.国网新疆电力有限公司电力科学研究院,新疆 乌鲁木齐 830011)
传统输电线路组塔施工中多采用落地平臂及摇臂抱杆[1-3]或流动式起重机[4-5]进行作业,组塔施工过程中的物料[6-8](如电动扭矩扳手、螺栓紧固件、组塔辅材)吊升,一般是将起吊绳索绕过抱杆顶部的起重滑车后,地面人员操控机动绞磨牵拉绳索进行起吊,起吊过程中辅以人力牵拉缆风绳对被吊物吊升姿态进行控制[9-10]。起吊过程中被吊物受风力及自身惯性作用,运动轨迹及吊升位置无法被精确控制,被吊物与铁塔可能发生碰撞从而掉落或受损,导致安全事故的发生。为解决上述问题,降低环境、人为因素在作业中的不良影响,研制专用的自动吊升装置就显得十分必要。基于电力施工中张力放线作业施工工艺[11-13],提出了一种电力组塔施工用货物三绳索吊升张力控制方法。建立了三绳索吊升张力控制力学模型,通过该模型可计算不同质量货物在不同吊升高度下绳索张力值;采用伺服控制[14-15]方式,搭建了三绳索吊升伺服张力控制系统,通过将理论计算得到绳索张力值输入到伺服控制系统中,可精确控制被吊物吊升轨迹及位置,保证了物料的安全起吊。
1 三绳索吊升张力控制原理
三绳索吊升张力控制系统工作原理如图1所示,定滑轮(作业现场为起重滑车)安装在电力铁塔主塔腿顶部,吊升装置主要由中间伺服张力起吊装置及左右两侧伺服张力牵拉装置组成。中间伺服张力起吊装置绳索绕过顶部定滑轮与吊升货物相连,连接位置位于被吊物上端;左右两侧伺服张力牵拉装置绳索对称分布,固定于吊升货物下端两侧,吊升过程中左右两侧绳索张力牵拉使得货物脱离主塔腿,防止吊升过程中货物与电力铁塔发生碰撞。

图1 三绳索吊升系统组成Fig.1 Composition of three rope hoisting system
2 三绳索吊升力学模型
2.1 模型建立
以新疆750 kV输电工程ZGU1型双回路直线鼓型角钢塔(2053B号)为例,建立三绳索吊升力学模型,如图2所示。定滑轮位于电力铁塔主塔腿顶部,主塔腿长度S=80 m,主塔腿与地面垂线夹角θ=6.3°,以主塔腿顶部垂向地面作z轴,建立如图2所示坐标系xyz。

图2 三绳索吊升力学模型Fig.2 Three rope hoisting mechanical model
中间伺服张力起吊装置绳索张力为T1,左右两侧伺服张力牵拉装置绳索张力为T2、T3。T1由地面绕过定滑轮主要起到吊升作用;T2、T3位于地面左右两侧对称位置,张力方向由被吊物指向地面伺服张力牵拉装置,通过T2、T3向外侧牵拉被吊物使其在吊升过程中脱离主塔腿一定的位移,避免货物在起吊过程中与主塔腿发生碰撞,同时三绳索张力牵拉使得货物产生一定刚度,能够抵御外部环境载荷对吊物产生扰动。
吊升过程中,假定货物质心与主塔腿脱塔距离始终保持恒定l=0.6 m,即货物吊升运动轨迹与主塔腿平行。定滑轮坐标A(0,0,80×cos 6.3),货物坐标B(0,yj,zj),T2对应C点坐标(x1,y1,0),T3对应D点坐标(-x1,y1,0),L为吊升过程中地面到货物在主塔腿上的投影长度。
2.2 模型求解
假定吊升过程中货物质心始终与倾斜主塔腿距离保持在l=0.6 m,则货物坐标(0,yj,zj)可表示为:yj=(80-L)·sin 6.3+l·cos 6.3,zj=L·cos 6.3+l·sin 6.3。对T1、T2、T3分别沿x、y、z3个方向进行分解,假定T1位于yz平面且力的方向与主塔腿平行,沿y轴及z轴方向分力如下:
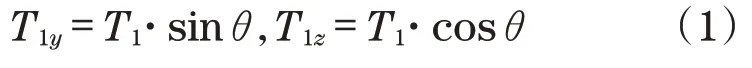
式中:θ为主塔腿与地面垂线夹角。T2沿x轴、y轴、z轴3个方向分力如下:

T2与T3对称分布且张力值相同,故T3在x轴、y轴、z轴3个方向分力值与T2在x轴、y轴、z轴3个方向分力值大小相同。其中T2x与T3x大小相等方向相反,T2y与T3y大小相等方向相同,T2z与T3z大小相等方向相同。T1牵拉装置位于y轴上,T2与T3位于xy平面且对称分布,如图3所示,则|x1|=R·cosγ,|y1|=R·sinγ。

图3 地面位置坐标Fig.3 Position coordinates on the ground
由上述可知,建立货物吊升过程中动态平衡方程如下:

式中:G为货物重力;m为货物质量;a为吊升过程货物加速度。
2.3 模型计算
T1对应起吊装置位于y轴即可,在主塔腿长度S一定时,匀速吊升过程中T1、T2、T3力值主要与地面装置安装半径R、安装角度γ、脱塔距离l、货物质量m相关联。在上述4个可变参数中选取1个为自变量,其余3个参数保持不变,通过在Matlab中构建方程组获得T1、T2、T3力值与可变参数关系。
假定安装角度γ=45°,货物质量m=100 kg,货物脱离主塔腿距离l=0.6 m。且R·sinγ>S·sinθ,即安装位置在y轴坐标大于主塔腿在y轴上投影坐标,则R>12.4 m。当安装半径R分别选取20 m、30 m、40 m、50 m时,T1、T2、T3力值分布如图4所示,伴随L增加三绳索张力值T均呈现单调递增趋势,伴随半径R增加,T1、T2、T3张力值均呈现减小。

图4 不同R下T1、T2、T3随L变化Fig.4 Variation of T1,T2,T3 with L under different R
假设安装半径R=30 m,货物质量m=100 kg,货物脱离主塔腿距离l=0.6 m,R·sinγ>S·sinθ,则90°>γ>17°。当安装角度γ分别选取30°、45°、60°、75°时,T1、T2、T3力值分布如图5所示,伴随L增加三绳索张力值T呈现单调递增趋势,伴随安装角度γ增加,T1、T2、T3张力值均呈现减小。
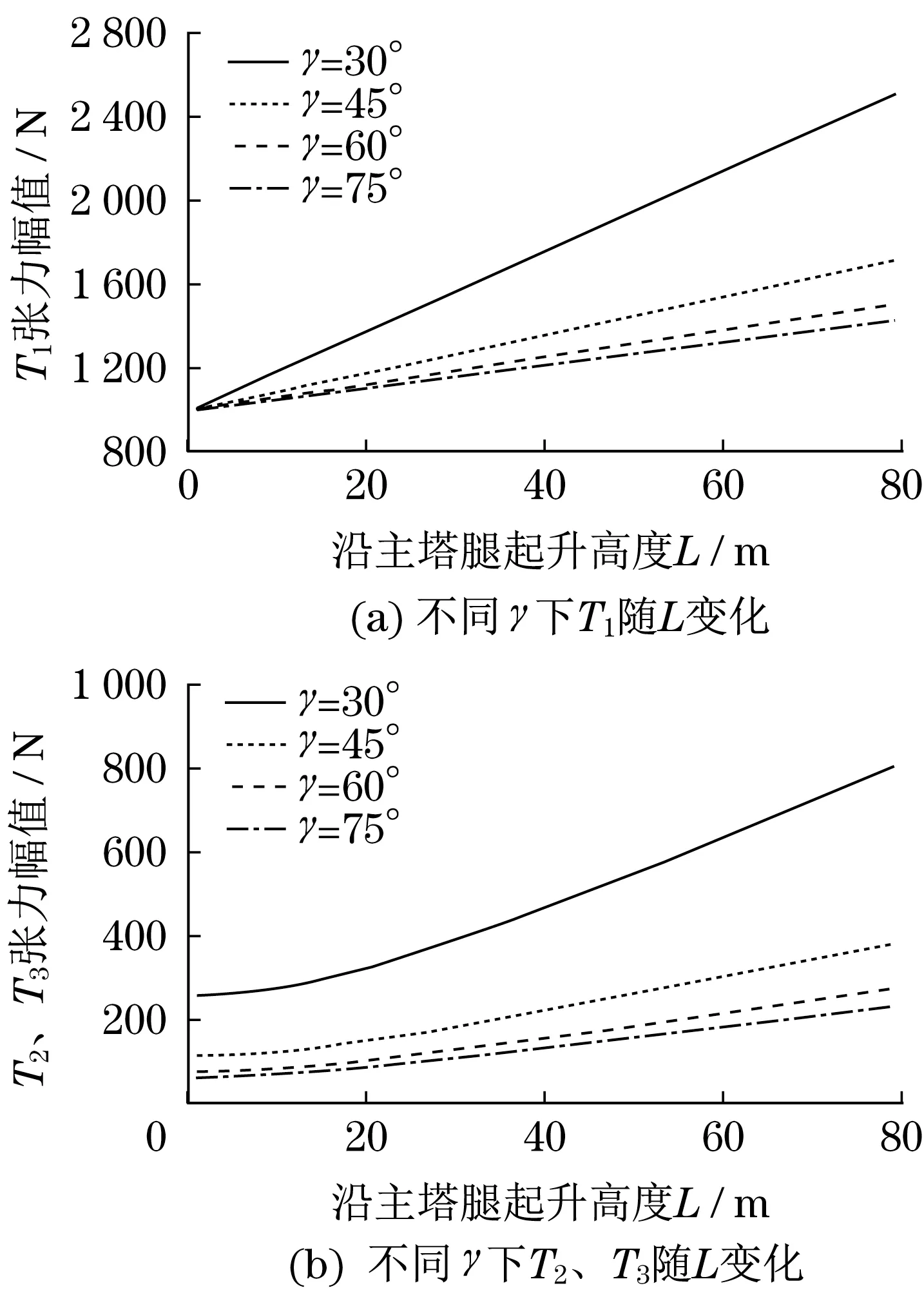
图5 不同γ下T1、T2、T3随L变化Fig.5 Variation of T1,T2,T3 with L under different γ
假设安装半径R=30 m,安装角度γ=45°,货物质量m=100 kg。当货物脱离主塔腿距离l选取0.6 m、1.0 m、1.4 m、1.8 m时,T1、T2、T3力值分布如图6所示,伴随L增加三绳索张力值T均呈现单调递增趋势,伴随脱塔距离l增加,T1、T2、T3张力值均增大,增大幅值较小,表明较小张力值增加可以产生较大的脱塔距离。

图6 不同l下T1、T2、T3随L变化Fig.6 Variation of T1,T2,T3 with L under different l
假设安装半径R=30 m,安装角度γ=45°,货物脱离主塔腿距离l=0.6 m。当货物质量m选取100 kg、200 kg、300 kg、400 kg时,T1、T2、T3力值分布如图7所示,伴随L增加三绳索张力值T均呈现单调递增趋势,伴随着货物质量m增大,T1、T2、T3幅值等比增大。

图7 不同m下T1、T2、T3随L变化Fig.7 Variation of T1,T2,T3 with L under different m
通过上述分析可知,任意工况下三绳索张力值T随着L的增加而增大,若保持货物吊升过程中脱塔距离l不变,当被吊物质量m、安装半径R、安装角度γ不同时,绳索张力值T均不同。当确定脱塔距离l后,不同质量m及不同安装半径R、安装角度γ下绳索张力值T随L的变化均可通过力学模型进行求解,该力学模型所求得的三绳索张力值T可作为伺服控制系统张力输入值。
3 试验验证
基于所建立的力学模型,搭建了三绳索吊升张力控制系统,并进行了室内试验验证。试验系统主要由中间伺服张力起吊装置、左右伺服张力牵拉装置、伺服张力控制柜、被吊物等组成。
室内吊升试验中,顶部定滑轮离地高度S=8 m,被吊箱体质量m=90 kg,顶部定滑轮与地面垂线夹角θ=6.3°的铅线作为脱塔基准,装置安装半径R=4.15 m,安装角度γ=45°,脱塔距离l=0.3 m。将上述参数代入到已建立的理论力学模型中进行计算,得到的T1、T2、T3数值如图8所示。将计算所得到的T1、T2、T3张力值通过人机操作控制界面进行输入,被吊物吊升过程位姿如图9所示。通过吊升试验可知,在整个起吊过程中,起吊及牵拉绳索张力值、被吊物作业位置及姿态与理论设定值保持一致,证明本文设计的三绳索吊升张力控制方法可靠,可进一步开展工程应用。

图8 模型计算张力值Fig.8 Tension value calculated by mechanical model

图9 三绳索吊升室内试验Fig.9 Three rope hoisting laboratory experiment
4 结论
(1)设计了一种输电线路组塔施工用三绳索吊升张力控制系统,该系统采用伺服控制模式,绳索张力值可根据被吊物质量及现场实际工况,在控制系统中进行设定,该系统保证了被吊物吊升过程中具有安全脱塔距离,实现了小型电力施工机具及材料吊升作业的自动化。
(2)基于张力控制原理,建立了三绳索吊升力学模型,不同质量货物在不同工况下的绳索张力值可通过该模型进行计算,计算值可保证被吊物按照预定轨迹进行吊升。
(3)基于理论及试验研究证实,本文设计的三绳索吊升张力控制方法,在货物吊升过程中其吊升轨迹及作业位置可控,电力组塔施工作业安全性得到提高,使得组塔施工作业更加智能化。
