基于自适应超螺旋滑模弹道跟踪控制方法

齐照辉, 张今, 王远卓,3, 王嘉, 徐梦荣, 张程

(1.航天飞行器生存技术与效能评估实验室, 北京 100089; 2.西北工业大学 航天学院, 陕西 西安 710072;3.北京航空航天大学 宇航学院, 北京 100191; 4.西安邮电大学 自动化学院, 陕西 西安 710121)

随着被攻击目标防御水平的提升，传统引战配合攻击目标的方式已经不能完全地摧毁目标。为解决上述问题，最好的制导控制思路是通过动能杀伤方式控制飞行器直接碰撞攻击目标[1]。对于非传统合作目标，常常需要以特定的弹道倾角在保证终端脱靶量条件下攻击目标[2]以达到最大毁伤效果。

近年来，国内外相关学者针对终端落角约束进行了大量的研究，归纳总结为以下3种：变系数比例制导控制落角、滑模变结构控制落角、最优控制落角。Lu等[2]在比例制导的基础上首创性地提出通过实时计算比例系数控制终端落角的方法；KUMAR等[3-5]提出了通过滑模变结构控制终端落角的思想；陈克俊等[6-7]通过最优控制的思想，在不考虑飞行速度变化的条件下提出了控制纵向终端落角的最优制导律。上述方法虽然对终端落角实现了一定程度的控制，但相对来说抗干扰能力差。

为解决上述问题，本文引入了滑模控制的思想。滑模控制对存在不确定性、干扰和未建模动态的系统具有较强的鲁棒性，尤其对末制导段强非线性系统具有较为良好的控制效果。Shtessel等[8]通过动态调整控制增益，提出了确保在有限时间内建立二阶滑模的方法。刘畅等[9]不仅利用李雅普诺夫函数证明了超螺旋制导律有限时间的稳定性，还给出了终端收敛时间的估计公式。Esfahani等[10]通过引入近似动态规划的方法提升了超螺旋滑模控制器的控制性能。但上述方法均没有将滑模控制器应用到标称轨迹的跟踪控制问题中。国内外文献表明，对标称轨迹进行弹道跟踪主要通过PID方法，但PID弹道跟踪法存在的问题是参数设定过于依赖经验。部分学者将LQR引入弹道跟踪控制问题中，Dukeman[11]提出了通过LQR跟踪标称状态(落角)的思想，但由于该方法采用的线性控制器与非线性模型存在较大的误差，故控制精度相对较低且抗干扰能力同样较差。

为解决上述问题，本文基于滑模非线性控制抗干扰的优点，结合基于两点边值问题建立的最优标称轨迹，提出了基于自适应超螺旋滑模跟踪控制方法用以对标称轨迹进行良好的跟踪。其中最优轨迹通过高斯伪谱法离散与非线性规划求解两点边值问题得到；滑模控制器采用自适应超螺旋算法用以实现对标称状态量的跟踪。

1 弹道跟踪模型构建与控制器设计

1.1 弹道跟踪控制模型建立

(1)

式中:V为导弹速度;θ为弹道倾角;x,y为2个方向的位置坐标;nx,ny为x方向和y方向的控制量[12]。g为重力加速度，取9.81 m/s2。

本文在进行跟踪控制器设计时，不考虑发动机推力特性，x方向位移由导弹速度决定，因此本文在进行跟踪控制器设计时，仅取弹道倾角θ和y方向坐标作为跟踪模型的状态变量，得到质点运动方程

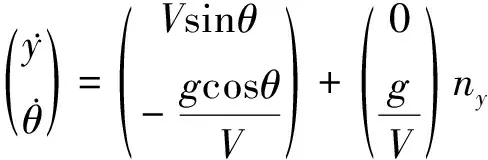
(2)

为实现对标称轨迹的跟踪控制，对上述跟踪问题，将实际弹道与标准弹道进行偏差计算，取偏差量为跟踪模型状态变量x，即

(3)

对(3)式求导，得[13]

(4)

式中,不受控变量V取相应时刻基准弹道上的状态值,用下标d标注。取过载偏差量Δny=ny-nyd为控制变量。令uy=Δny,上述模型可转化为

(5)

至此建立了弹道跟踪控制模型。

1.2 最优标称轨迹的建立

考虑到初始状态和终端状态((1)式中的4个状态)约束,最优标称轨迹的建立是一个典型的两点边值问题。性能指标选取为

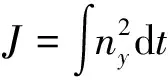
(6)

(6)式性能指标的选取,保证了标称控制指令较为光滑,不会出现抖振较大的现象,保证了工程实现的可行性。

最优标称轨迹的建立流程如下:考虑到微分方程中各状态数值相差较大的特性,对(1)式各状态进行归一化处理[14-15],以保证后续数值计算不会出现矩阵条件数较大(奇异)的问题,通过高斯伪谱法将微分状态方程离散,利用非线性规划方法得到最优标称轨迹,并利用数值验证最优性条件。

本文建立的标称轨迹如图1～2所示,可以看出整个标称轨迹较为光滑,没有出现控制量抖振较大的现象。需要注意的是:所建立的标称轨迹为开环的最优标称轨迹,故需要设计一种跟踪律对标称轨迹进行跟踪控制以保证终端状态满足要求。

图1 标称弹道轨迹

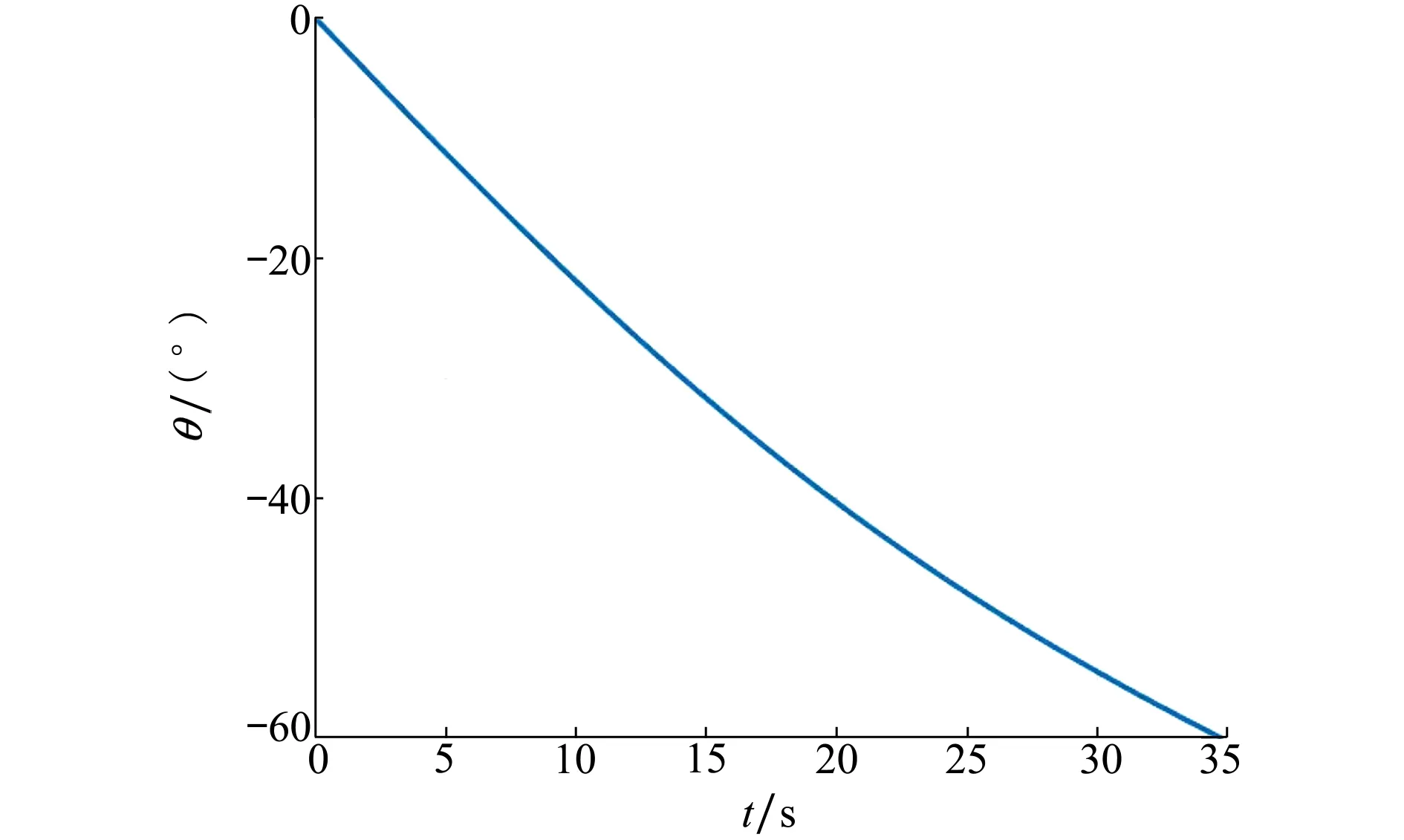
图2 标称轨迹弹道倾角

1.3 自适应超螺旋滑模算法

定义非线性系统跟踪问题为

y=s(x,t)

(7)

式中:x∈X⊂Rn为系统的状态变量;v∈U⊂R为控制器的输入,函数f(x)和g(x)是未知但有界的非线性函数,y是系统输出值。定义s(x,t)为滑模变量,通过设计使滑模变量s→0时,y→0。

滑模控制器的核心思想是当系统存在不确定性和外部扰动的情况下,设计系统控制输入v使滑模变量s在有限时间内收敛到0,进而使系统输出状态y趋于0。需要注意的是,滑模变量s的定义是基于控制目标y和其相对阶定义的[16]。假设系统的相对阶为1,对滑模变量s求导得到

(8)

式中,a和b为未知但有界的函数,满足|a|≤aM,0≤bm≤b≤bM。对于x∈X且t>0:aM,bm和bM为正常数。

基于上述假设,考虑到滑模控制的目标是设计控制输入v使滑模变量s在有限时间内趋于0,故使用如下的超螺旋算法[17]

(9)

式中,k1和k2为控制器增益,取值均大于0,w为中间参数,w(0)=0。当满足(10)式所述条件时

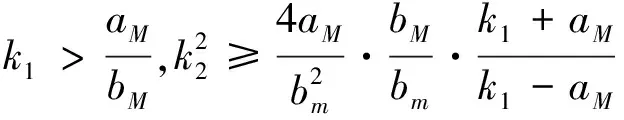
(10)

为解决上述问题,使用自适应增益的策略,使控制器增益随着控制精度的变化而变化:当控制精度满足要求时,通过减小增益降低滑模控制量的抖振;当控制精度较低时,通过增大增益来提高控制精度。本文采用自适应超螺旋控制器(adaptive super-twisitng,ASTW)[8,18]来解决导弹跟踪控制中的外部干扰问题,提高了控制精度。针对(9)式中增益k1和k2的自适应律设计如(11)式所示

(11)

式中,k1m,ε,χ,μ和k为正常数。此外,k1的初始状态k1(0)>k1m。上述自适应增益的设计思想为:

1) 如果|s|>μ,则控制精度低于由μ定义的期望精度值。此时控制器的增益较低,故根据(11)式,k1和k2应增大;

2) 如果|s|<μ,则控制精度较高。此时控制器的增益较大,故根据(11)式,k1和k2将减小;

3) 参数k为一非常小的正常数,其作用是保证k1为正。

上述方法的稳定性证明参考文献[8,18]。

1.4 跟踪控制器设计

针对(5)式,考虑到该问题通过ny控制高度y与弹道倾角θ,故该问题是典型的欠驱动问题,因此,本文设计滑模面为

s=βsigα(x1)+λ1x1+x2

(12)

式中,α∈(1,2),sigα(x1)=|x1|αsign(x1)。

对(12)式求导得到

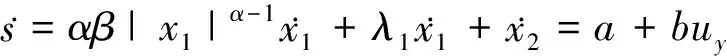
(13)

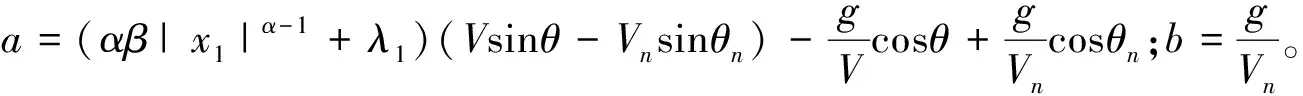
因为系统的相对阶假设为1，根据自适应超螺旋算法，本文设计的控制器为

(14)

式中，v同(9)式所示。为验证(14)式设计的控制器能满足滑模变量s趋近于0，将(14)式代入(13)式，(13)式可化为

(15)

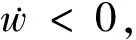
2 算例分析

2.1 模型验证

根据文献[13]可知，导弹的速度特性已知，故本文不考虑对导弹速度与x方向的位置进行控制，只对4个状态中的2个进行控制。初始和期望终端状态设定见表1。

表1 初始和期望终端状态设定

基于表1所述的两点边值问题，通过高斯伪谱法离散微分方程并通过非线性规划得到两点边值问题的最优解，标称轨迹如图3～6(图中蓝色虚线曲线)所示。

图3 导弹飞行轨迹 图4 导弹过载随时间的变化曲线图5 导弹弹道倾角随时间变化曲线

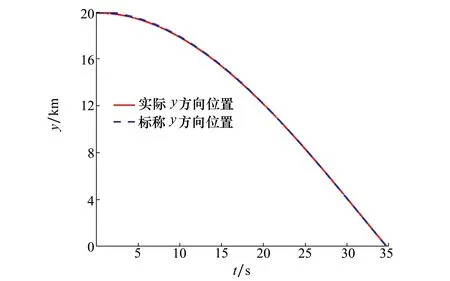
图6 导弹y方向位置随时间的变化曲线

根据上文所建立的标称轨迹，通过滑模超螺旋控制器控制导弹在存在初始状态偏差(y方向位置偏差100 m，初始弹道倾角偏差3°)的情况下对标称轨迹进行跟踪。

根据上文自适应参数的思想，超螺旋滑模控制器的参数设定如表2所示。

表2 控制器参数设定

控制器跟踪标称轨迹的结果如图3～6的实际曲线(图中红色曲线)所示。从图3可以看出跟踪轨迹不仅整体较为光滑，还对标称轨迹实现了良好的跟踪。从图4可以看出，在考虑控制限幅的情况下，控制量曲线很快收敛到标称控制曲线，整体跟踪控制量较为光滑，跟踪效果较好。图5和图6的跟踪曲线表明在存在初始状态偏差的情况下，实际状态很快收敛到标称状态。终端误差如表3所示。

表3 滑模弹道跟踪法终端误差表

从表3可以看出在存在初始状态偏差的情况下，终端状态误差值均较小。故所提出的基于标称轨迹的超螺旋滑模跟踪控制器具有较好的控制效果。

2.2 方法对比验证

为验证基于自适应超螺旋滑模弹道跟踪控制方法的优越性与先进性，需要与不同方法进行对比。文献中常通过PID或LQR对标称轨迹进行跟踪控制，故本文通过在标称轨迹离散点设计多个LQR控制器作为对比方法进行验证。

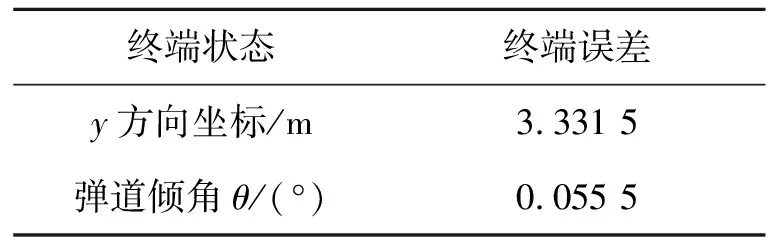
表4 LQR弹道跟踪法终端误差

相比于表3滑模弹道跟踪法所示的终端误差，从表4可以看出LQR弹道跟踪法高度误差较大，故LQR弹道跟踪法的精度相对较低，适用性相对较差。

2.3 蒙特卡罗仿真

为验证基于标称轨迹的超螺旋滑模跟踪控制器方法的抗干扰性能，本文通过蒙特卡罗法仿真验证了在存在不同初始状态偏差情况下的仿真效果。

本文随机生成满足正态分布的初始偏差状态值如表5所示。

表5 随机初始状态偏差设定

根据表5所示的随机初始状态偏差设定，本文通过不同次数(10,100,1000)的蒙特卡罗模拟验证方法的性能。模拟结果如图7～9所示。

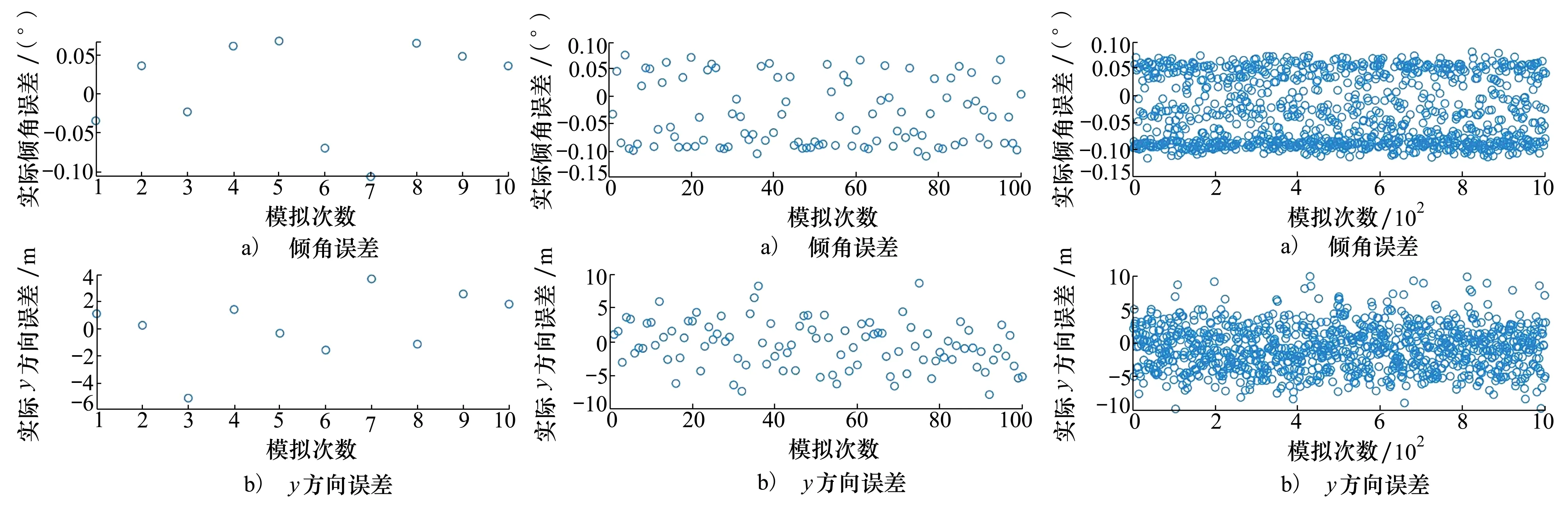
图7 10次蒙特卡罗模拟 图8 100次蒙特卡罗模拟 图9 1 000次蒙特卡罗模拟

从图7～9可以看出，2个终端状态的误差均较小且分布较为均匀。终端y方向误差基本控制在10 m以内，终端弹道倾角θ误差基本控制在0.15°内。

为了定量有效分析整体蒙特卡罗仿真数据的结果，计算实验数据的均值与方差如表6所示。

表6 仿真数据的均值与方差

从表6可以看出，2个状态误差的均值与方差均较小，能满足导弹控制终端位置与终端角度的要求。针对不同初始状态的偏差，所提出的基于标称轨迹的超螺旋滑模跟踪控制方法终端误差较小，抗干扰性能较好，体现了滑模超螺旋跟踪控制律的优越性。

2.4 仿真结果分析

在初始状态偏差不太大的情况下，基于自适应超螺旋滑模跟踪控制器跟踪效果较好(终端误差较小)且控制量相对较为光滑，稳定跟踪后没有出现控制量饱和的现象。

从蒙特卡罗法仿真的结果可以看出，该方法在不同初始状态偏差(干扰)下终端位置与角度误差均较小，控制效果良好，故该方法具有相对良好的抗干扰性能。

3 结 论

本文通过求解两点边值问题建立最优标称轨迹，结合滑模超螺旋控制器思想，提出了基于自适应超螺旋滑模跟踪控制器设计方法，实现了二维平面内标称轨迹的跟踪控制问题。本文的主要结论如下：

1) 本文通过高斯伪谱法离散微分方程,并通过非线性规划求解两点边值问题得到开环最优标称轨迹。因标称轨迹是最优的，故所提出的基于标称轨迹的超螺旋滑模跟踪控制方法具有接近最优的特性。

2) 由于超螺旋滑模跟踪控制律具有较强抵抗外界干扰的能力，在初始状态偏差不太大的情况下，滑模控制律可以控制导弹轨迹与制导指令曲线很快收敛到标称值。不同次数的蒙特卡罗模拟结果表明终端状态偏差的误差均较小，位置误差控制在10 m以内，倾角误差控制在0.15°内，整体控制效果较好。