面向重心、质量变化的自适应飞行控制律设计与半物理实时仿真验证
2022-11-08李煜刘小雄黄伟李珂澄明瑞晨章卫国
李煜, 刘小雄, 黄伟, 李珂澄, 明瑞晨, 章卫国
(1.西北工业大学 自动化学院, 陕西 西安 710129; 2.陕西省飞行控制与仿真技术重点实验室, 陕西 西安 710129)
作为飞机重要参数,重心变化直接影响飞机的稳定性和操纵性能,例如,运输机重装空投、战斗机导弹发射。重心的变化会导致飞机纵向和横航向通道间的耦合,当重心变化超出预定的安全范围,会降低飞机稳定裕度,更有甚者会造成飞行事故。因此,从控制的角度提高飞控系统对重心、质量变化的鲁棒性,对提高飞机安全飞行具有重要意义。
针对重心变化过程中的控制问题,张晶等[1]提出一种非线性滑模自适应控制方法,基于此方法设计的姿态控制律能够在重心变化下依旧达到预期动态性能。杨晓科等[2]以重装空投为背景,考虑飞机重心位置和质量的变化,借助干扰观测补偿的思想设计了姿态控制器,用于观测、补偿重心位置和质量变化的影响,进而保证重装空投过程中的飞机姿态满足任务需求。韩婵等[3]基于预估模型参考自适应控制设计了姿态控制律,提高了系统对重心偏移的适应能力。此外,Li等[4]基于角加速度估计的增量动态逆方法设计了鲁棒角速度控制器,仿真结果表明该控制器能够有效克服重心突变、缓慢变化对飞机的干扰,实现了重心变化下预期的角速度动态。
得益于自适应控制灵活的结构和优秀的鲁棒性,大多数学者都采用自适应策略来解决飞机扰动影响下的飞行控制问题。作为一种典型的自适应控制方法,Cao在2006年提出了一种L1自适应控制[5]。该控制方法解决了传统模型参考自适应控制中快速性与鲁棒性矛盾的问题,实现了快速自适应的同时保证系统对干扰的鲁棒性。该方法自提出以来,受到了国内外学者的广泛关注。得益于这些优点,L1自适应控制理论自提出以来得到了很好的发展[6-7],并且被应用于多种飞行控制领域中[8-10]。
考虑到飞机重心、质量变化的不确定性,本文结合反馈线性化方法对L1自适应控制进行改进,并基于改进后的非线性L1自适应控制方法设计鲁棒飞行控制器,以保证飞机重心、质量变化干扰下的鲁棒性和稳定性。此外,借助硬件在环(hardware in loop, HIL)飞行控制半物理仿真实验平台对本文设计控制律的性能进行验证。实验结果表明,本文提出的非线性L1自适应控制器提高了飞控系统的鲁棒性,能够有效克服重心突变对飞机产生的影响,并且在这过程中能够同时保证飞机的稳态和瞬态特性。本文的研究对于提高飞机的安全飞行具有一定的工程应用价值。
1 重心变化的飞行器建模
假设飞机是质量分布均匀的刚体,以地面系为惯性系,以牛顿第二定律为基础,结合微元法推导飞机在质量、重心变化时的线运动和角运动方程[1,11],其结果如下:
式中:m表示当前时刻飞机的质量;Ixx,Iyy,Izz和Ixy,Ixz,Iyz为当前时刻飞机的转动惯量和惯性积,具体表达如下
(3)
Δm表示飞机质量变化,下标0表示重心变化前的状态量。
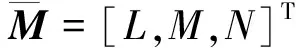
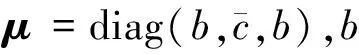
(1)式和(2)式表明重心偏移致使线加速度和角加速度相互耦合,使得飞机的动力学更加复杂。并且随着重心的偏移,纵向和横航向的角速度运动也相互耦合在一起。进一步整理(1)式和(2)式,角速度和线速度动态的矩阵形式为
式中

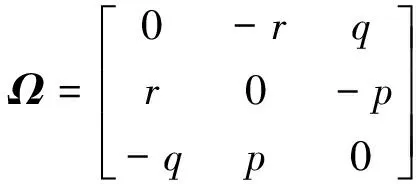
(8)
此外,侧滑角微分方程为
(9)
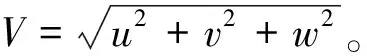
2 整体控制策略和方法
重心变化对飞机纵向和横侧向的力和力矩都产生影响。假设飞机质量和重心变化未知,将其对飞机的影响视为扰动。本文基于非线性L1自适应控制方法来设计飞行控制律,提高飞行控制系统的鲁棒性,进而克服重心、质量变化产生的扰动,使得飞机在重心变化下具有良好的控制性能。本文以F-16缩比战机为模型,具体参数参见表1。
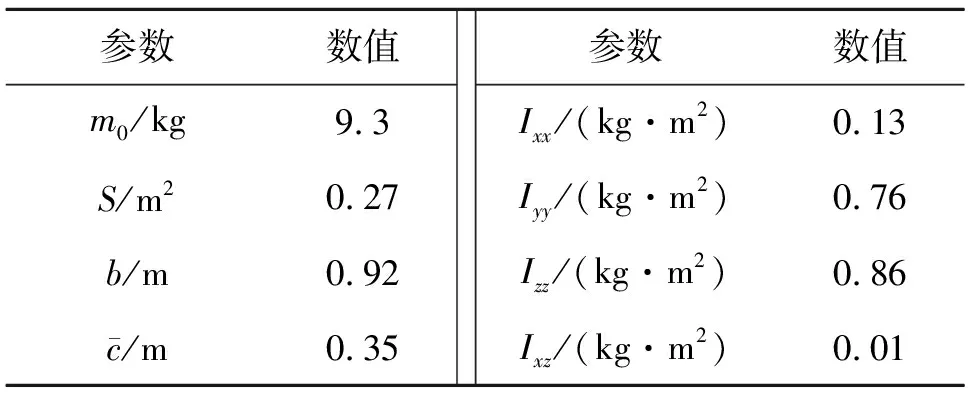
表1 F-16缩比飞机参数
操纵杆对应飞机的俯仰和滚转运动,油门杆控制飞机的飞行速度,脚蹬则用于消除飞机的侧滑角。由于响应速度的不同,采用级联控制策略实现对飞机侧滑角的控制,即侧滑角控制律生成偏航角速度指令,而角速度控制器根据偏航角速度指令给出舵面指令,最终实现侧滑角控制。
采用非线性L1自适应控制方法设计角速度控制律,进而提高飞控系统的鲁棒性。由于侧滑角动态与偏航角速度存在明显的显式关系,采用积分式动态逆控制策略设计侧滑角控制律。采用比例积分式控制策略设计速度保持控制律,进而克服因重心变化而对线速度产生的扰动,保证飞行时飞机速度的稳定。飞行控制系统整体框架如图1所示。
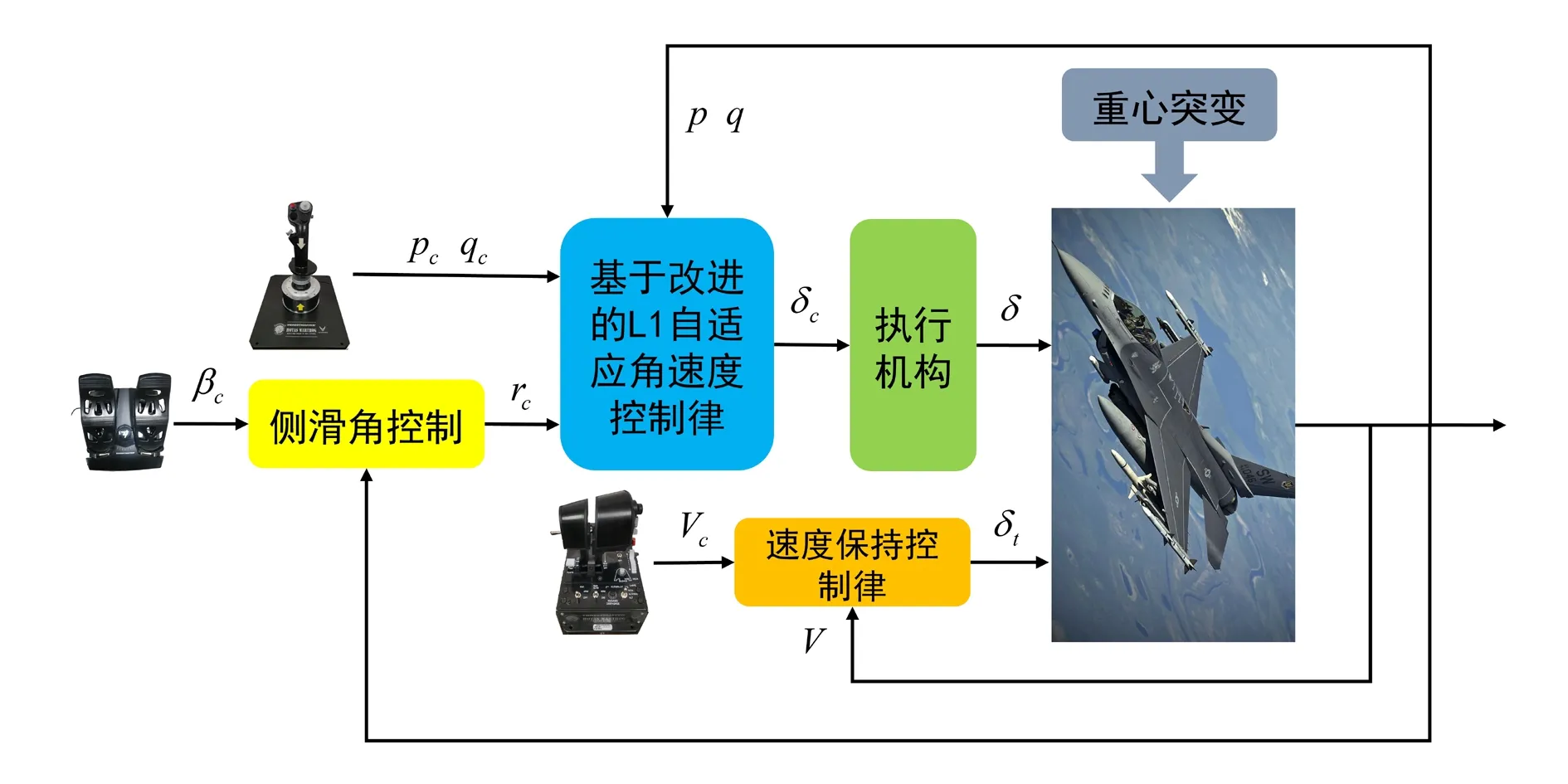
图1 整体控制框架
传统L1自适应控制往往是围绕单个状态点展开控制律设计。当系统状态偏离该点时,系统状态变化产生的非线性动态增量被L1控制器视为干扰,这在某种程度上会削弱控制器性能,从而降低控制器对外部干扰的鲁棒性。
模型的非线性动态可通过离线建模获得,因此引入反馈线性化来改进L1自适应控制系统,旨在通过非线性逆控制消除已知系统的非线性项,从而改善系统动态,达到简化系统动态的目标。而L1自适应控制用于克服未建模动态、模型不确定性以及外部扰动的干扰影响,进一步在飞行包线内提高系统的鲁棒性。
3 基于非线性L1自适应角速度控制
3.1 角速度控制律设计
角速度运动方程(6)可写成仿射非线性的形式,具体如下
(10)
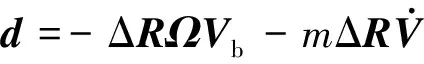
从结构上来看,非线性L1自适应控制器仍分为被控对象、状态预测器、自适应律以及带有低通滤波器的控制律4个部分。
根据(10)式,可将角速度运动方程重写为

(11)
式中,λ表示输入增益矩阵,通常满足λii∈[0,1],i=1,2,3。σG-1d表示与输入相匹配的扰动。
状态预测器根据控制输入来预测当前状态的期望动态,因而为系统提供参考,具体设计如下
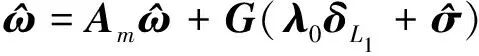
(12)

非线性L1自适应控制律设计如下
δ=δL1+(Gλ0)-1(Amω-f)
(13)
式中

kg=-G-1Am
(14)
式中,L-1[·]表示Laplace反变换。ωc表示角速度指令。kc为滤波器增益,与D(s)构成低通滤波器C(s)

(15)
滤波器中kc和D(s)的选择必须满足L1稳定条件[12]:存在ρr满足‖ω‖<ρr,那么kc和D(s)必须满足(16)式

(16)
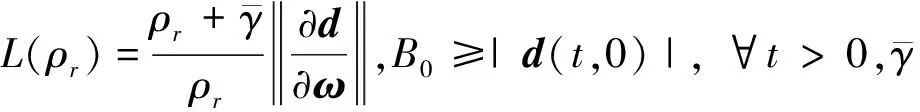
H1(s)(sI3-Am)-1G
H2(s)(sI-Am)-1G(1-C(s))
(17)
详细的证明过程参考文献[12]。非线性L1自适应控制继承了L1自适应控制的优点,能够解决传统自适应控制中鲁棒性与快速性矛盾的问题,即保证系统鲁棒性的同时,兼顾了系统响应的快速性。此外,非线性L1自适应控制能够消除已知与状态相关的非线性项,因而避免系统已知非线性对系统的影响,进一步扩大了控制器的适用范围。
基于分段常数的自适应律是一种结构简单、计算量小的自适应律,该算法能够在保证系统稳态性的同时兼顾系统的瞬态性能。文献[13]对分段常数自适应算法进行了改进,解决了分段常数自适应律中采样时间和估计精度不匹配的问题。因此,本文采用改进的分段常数设计自适应律,具体如下
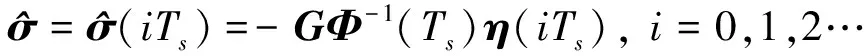
(18)
式中,Φ(Ts)和η(iTs)定义如下
Φ(Ts)=Am-1(eAmTs-I3)
(19)

综合以上设计,图2展示了完整的基于非线性的L1自适应角速度控制的结构框图。
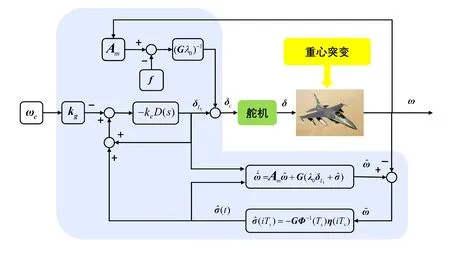
图2 基于非线性L1自适应角速度控制结构
3.2 系统性能分析
在控制器(13)的作用下,根据角速度动态(11)与状态预测器(12)可以推导出角速度跟踪误差
(20)


(21)

(22)
式中
角速度在(j+1)Ts时刻下的跟踪误差记为
(25)
在改进分段常数自适应律的作用下,角速度跟踪误差可进一步简化为

(26)
进一步推导角速度误差与采样时间之间的关系,(26)式的范数形式可表示为
(27)
式中
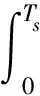
(28)
‖G-1(I3-λλ0)-1Am‖ρr
(29)
(27)式得到的角速度上界对所有(j+1)Ts≤τ都成立,因此对于iTs≤τ,则
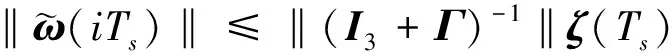
(30)
那么,(22)式中角速度误差的范数为
式中
(33)
当采样时间Ts不断减小,(33)式的极限为
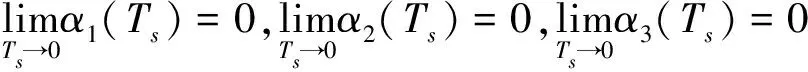
(34)
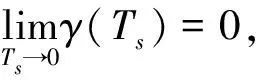

(35)
所以对于任意t∈[0,τ],都有

(36)
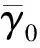
从(35)式和(36)式来看,在非线性L1自适应控制器的作用下,闭环系统的角速度误差有界。并且,通过增大自适应增益Γ能够缩小角速度的跟踪误差。这表明改进的分段常数自适应能够在固定采样时间Ts下,通过调整自适应增益来实现满意的自适应估计精度,因而克服传统分段常数自适应律(Γ=0)仅通过缩小采样时间来减小误差边界的缺点,减轻了硬件的负担。
在重心、质量变化扰动的影响下,基于改进的分段常数自适应律在固定采样间隔Ts内能够保证飞机角速度的稳定性,因而在整个控制过程中,系统的全局稳定和瞬态性能都得到了保证。
4 侧滑角与自动油门控制律
由于飞机侧滑角动态要慢于偏航角速度,根据奇异摄动理论,侧滑角控制可以在角速度基础上构建完成,即偏航角速度作为内环,而侧滑角为外环。侧滑角动态和偏航角速度存在显式对应关系

(37)
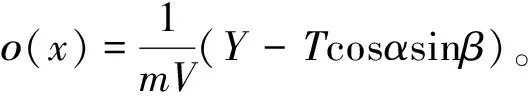
采用积分式动态逆控制方法设计侧滑角控制律。具体如下

(38)
式中,νβ为侧滑角的虚拟控制,表示侧滑角的期望动态,具体设计如下
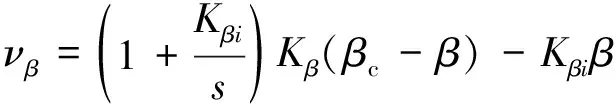
(39)
式中,下标c表示指令,Kβ和Kβi分别为比例和积分增益。
由于飞行员在驾驶飞机的过程中往往不期望出现侧滑角,在不考虑大机动的情况下,β通常很小,因此ο(x)可以合理忽略[14]。当飞机处于大侧滑状态,可通过控制律中积分器来消除此项影响。
积分式侧滑角动态逆控制框图如图3所示。
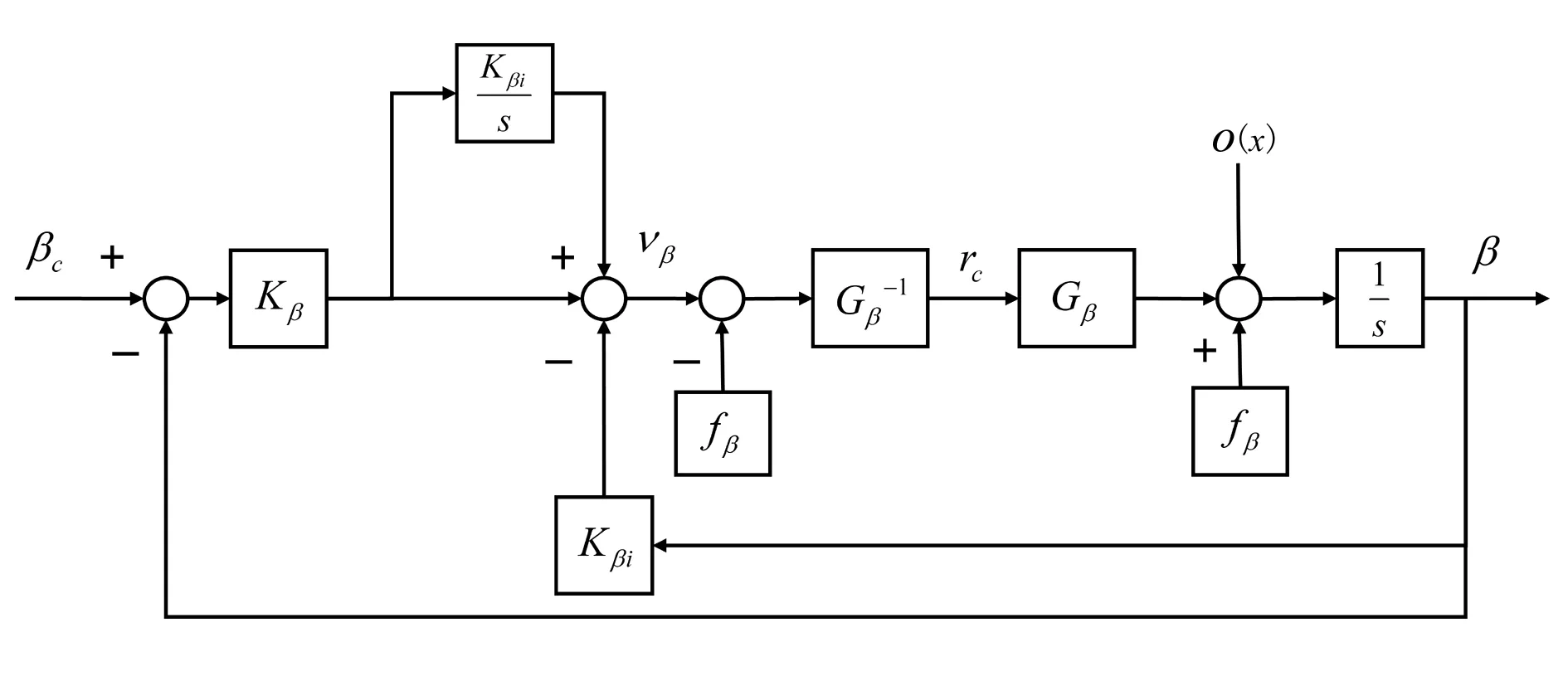
图3 侧滑角控制框图
当侧滑角较小时,ο(x)可以忽略。侧滑角系统的传递函数为

(40)
此时,侧滑角动态为带宽为Kβ的一阶惯性环节。当侧滑角较大时或者存在干扰情况下,扰动对系统的影响为

(41)
选择合适比例和积分增益可使阻尼比满足要求,能消除干扰产生的稳态误差,从而提高侧滑角控制系统的鲁棒性。
采用比例-积分式控制器设计自动油门控制器。该控制律据速度响应误差调整油门开度δth实现对飞机的速度控制,具体设计为
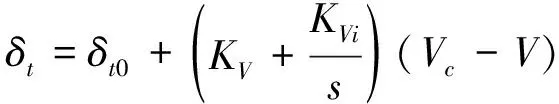
(42)
在控制律中,δt0为初始配平的油门开度,油门开度被限制在[0,1]之间。同样,KV和KVi分别为比例和积分增益。
5 HIL半物理仿真验证
硬件在环飞行控制半物理仿真实验平台(以下简称HIL实验平台)包括操纵机构、地面站、自动驾驶仪、工控机以及虚拟视景软件5个部分,HIL实验平台结构如图4所示。
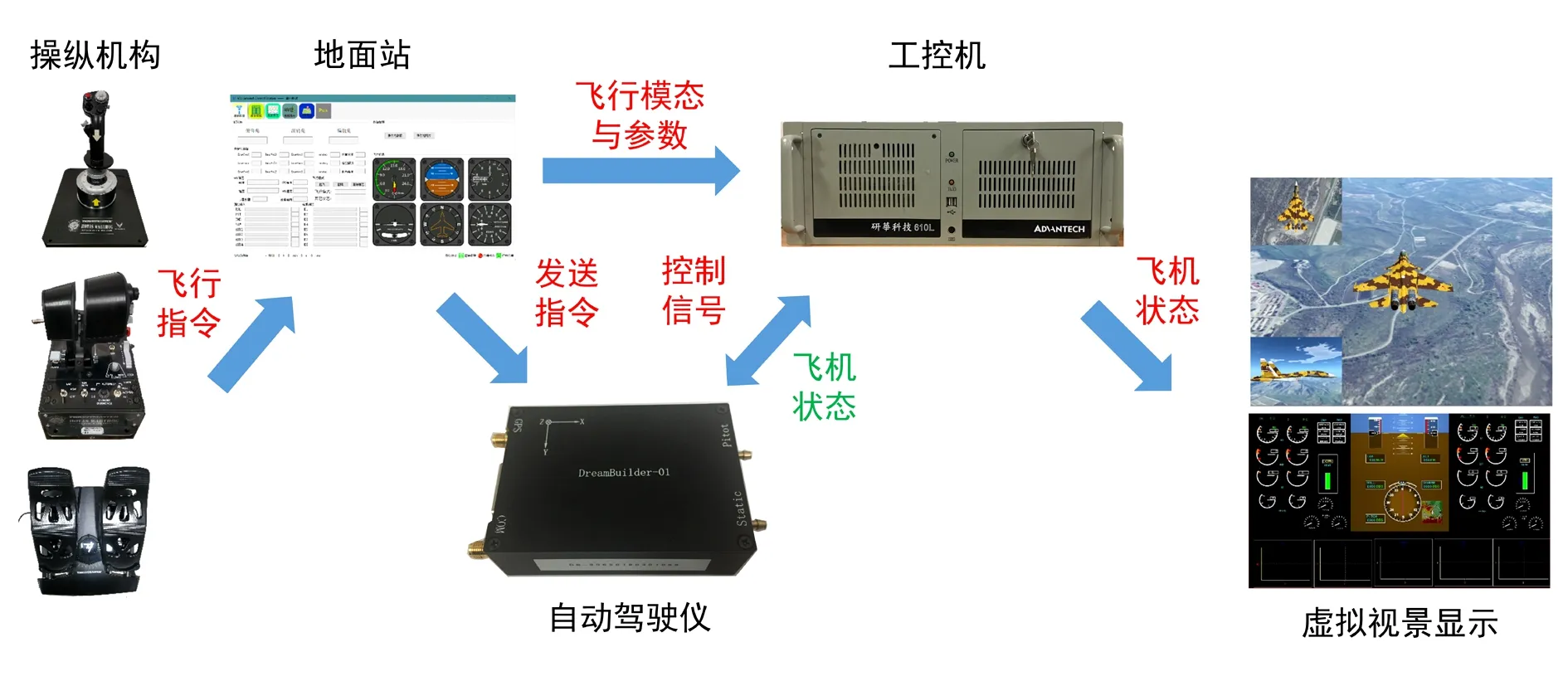
图4 HIL飞行控制半物理仿真实验平台架构
在HIL实验平台中,驾驶杆、脚蹬和油门用于产生飞机运动指令,地面站接收操纵机构的指令并通过RS232接口发送到自动驾驶仪。此外,地面站还能实时设定飞机状态和参数,进而使平台能实现多任务飞行场景的模拟。自动驾驶仪根据收到的操纵指令和飞机状态,通过所设计的鲁棒飞行控制律解算出舵面偏转,并通过RS232接口发送给工控机。工控机包含舵机和非线性飞机模型,因而,可用于模拟多场景下六自由度实际飞机的运动。工控机将飞机飞行数据通过UDP网口实时发送给虚拟视景软件以实时显示飞机姿态和运动轨迹,使实验者能够深入、直观地了解飞机的运动。
在工控机中,采用一阶惯性环节来模拟执行机构,执行机构的角度与速率限制详见文献[15]。
在HIL实验平台中,地面站接收和发送杆指令的频率为100 Hz,自动驾驶仪中控制律解算频率为50 Hz,工控机中状态更新频率更新为100 Hz。
飞机初始以高度4 000 m和50 m/s的速度直线平飞。飞机初始状态如表2所示。

表2 飞机平飞时状态


图5 重心突变下,俯仰角速度以及误差对比图 图6 重心突变下,滚转角速度以及误差对比图
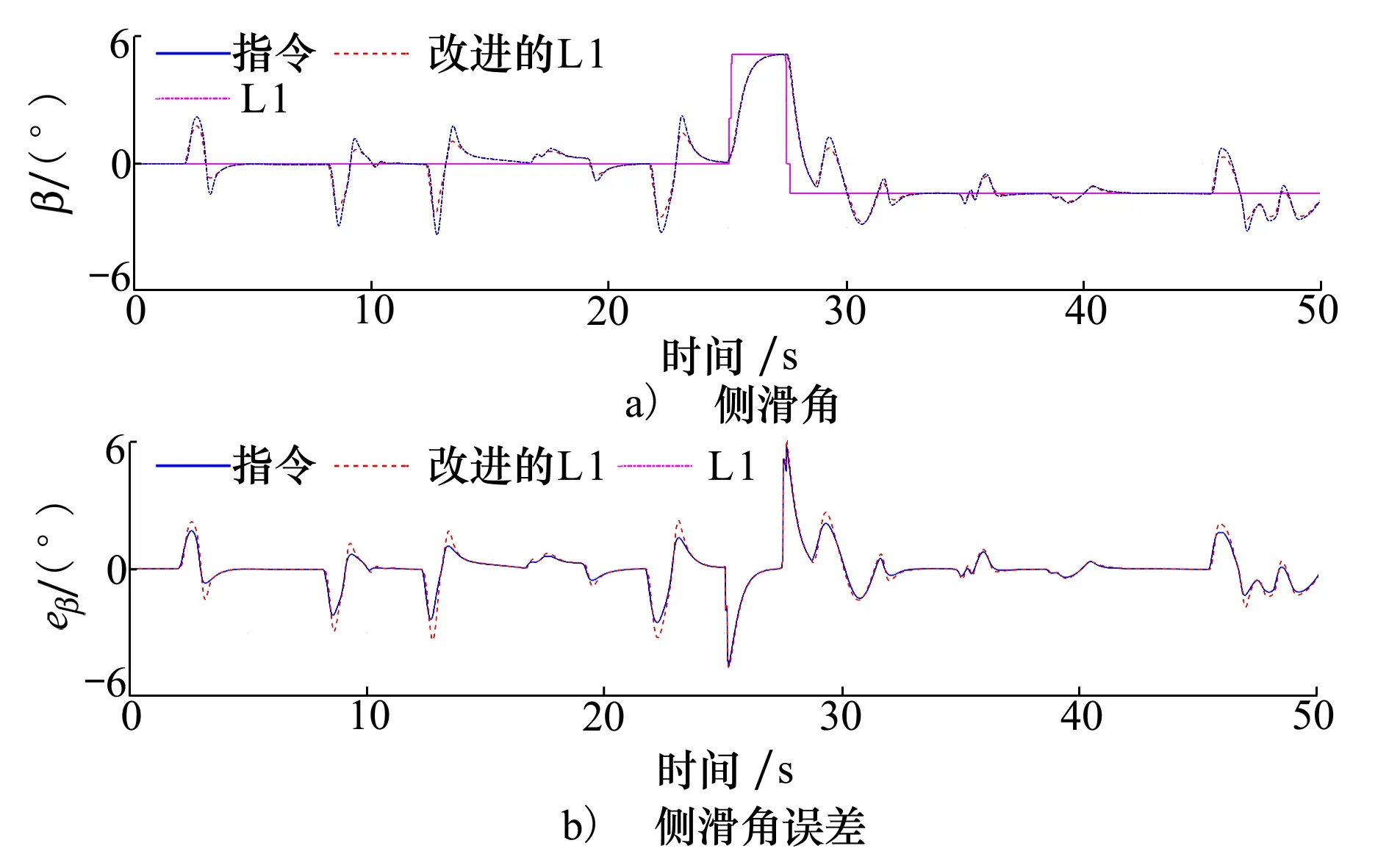
图7 重心突变下,侧滑角及误差对比图
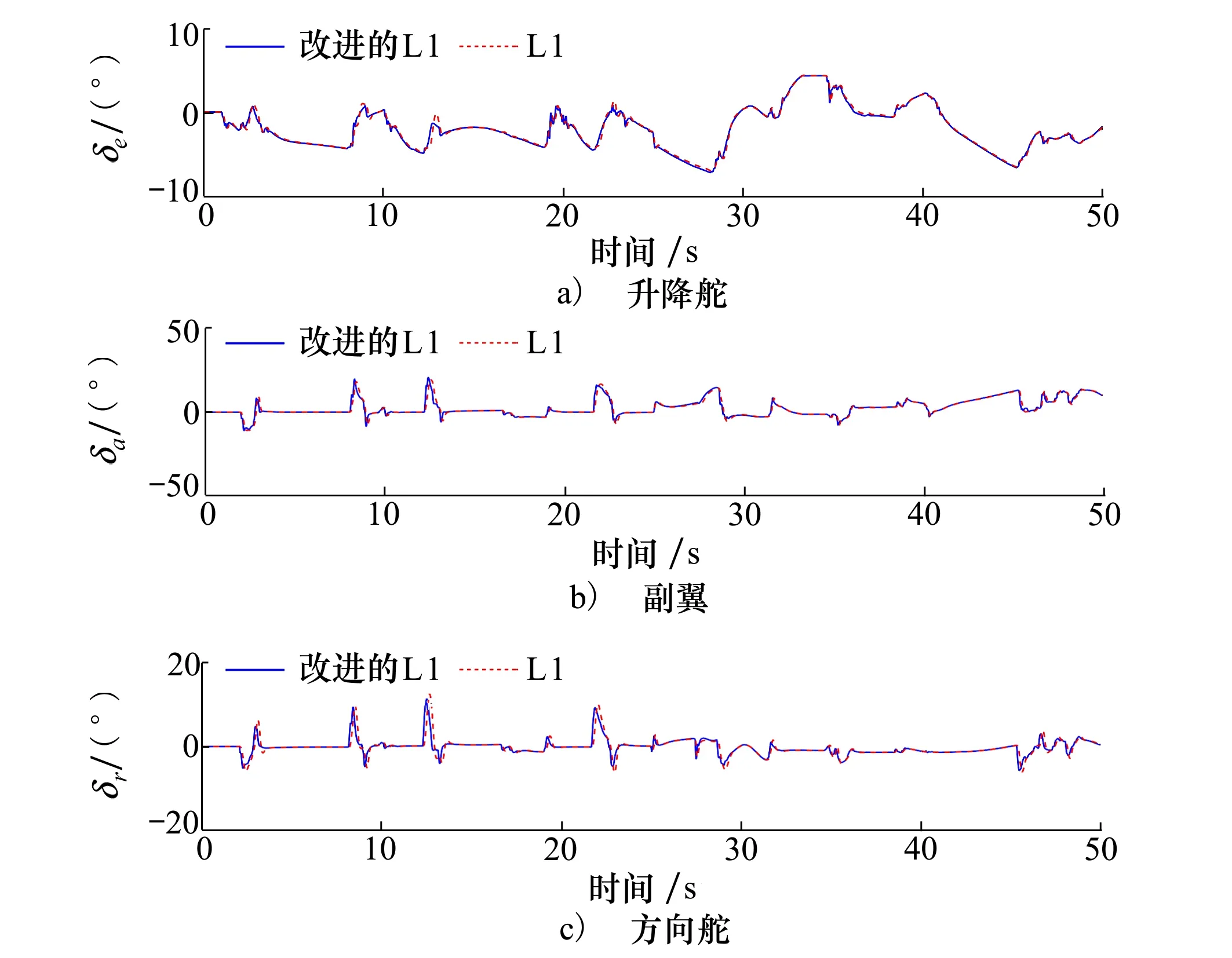
图8 舵面输入对比
从仿真结果来看,本文提出的非线性L1自适应控制继承了L1自适应控制快速性与鲁棒性解耦的优点。在重心突变干扰下,2种控制器都能够有效克服重心、质量突变产生的影响,实现对参数不确定变化的快速补偿,保证飞机的稳定性。但从动态性能来看,非线性L1自适应控制在重心突变下的动态误差相比更小。为了进一步分析控制性能,表3统计角速度和侧滑角误差的均值和方差。
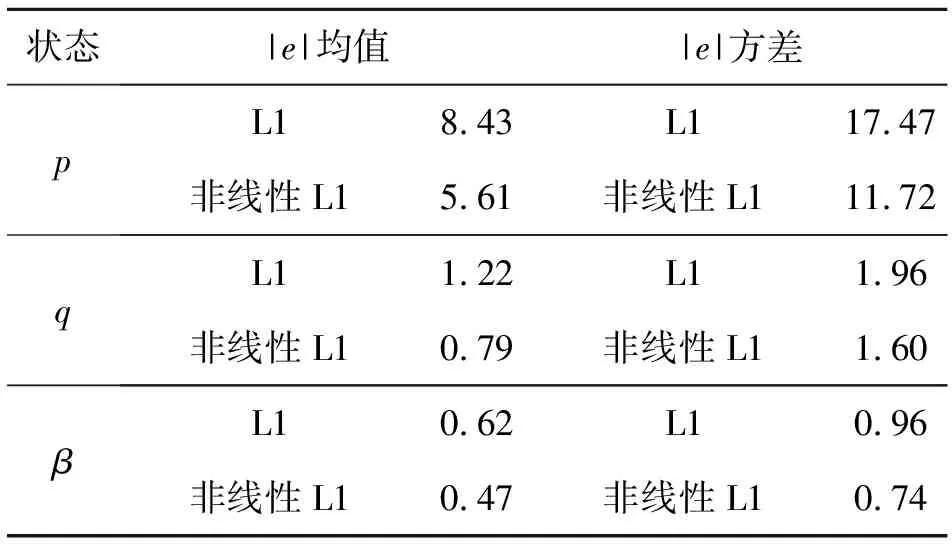
表3 误差绝对值的均值和方差
从误差统计来看,非线性L1自适应控制器下的俯仰、滚转角速度以及侧滑角误差的均值和方差都明显小于L1自适应控制器,表明非线性L1自适应控制器准确性更高。此外,从侧滑角动态来看,非线性L1自适应控制器对横航向解耦能力也较L1自适应控制有所提升。综合以上分析,非线性L1自适应控制器的控制性能够达到预期的要求,在削弱重心突变干扰的情况下,能实现更准确的指令跟踪。
6 结 论
本文考虑重心、质量突变对飞机影响,提出一种基于非线性L1自适应控制的方法,并基于此方法设计了鲁棒飞行控制律。该方法在传统L1自适应控制的基础上引入反馈线性化策略,用于消除已知飞机的非线性动态影响,进而提升控制器对外部扰动的鲁棒性。非线性L1自适应控制具备L1自适应控制快速自适应的优点,并且进一步提升了控制系统对外界干扰的鲁棒性。最后,在HIL仿真实验平台对所设计非线性L1自适应飞行控制律进行半物理仿真实验,实验结果表明:所设计的非线性L1自适应控制器能够克服重心、质量突变对飞机产生的干扰,并且在受扰后仍具有良好的控制效果。
