基于用户满意效用的空间众包任务分配方法

彭鹏，倪志伟，朱旭辉

（1.合肥工业大学 管理学院，合肥 230009；2.北方民族大学，银川 750021；3.过程优化与智能决策教育部重点实验室（合肥工业大学），合肥 230009）

0 引言

随着“互联网+”发展和智能客户端的普及应用，出现了很多需要供需双方到达特定时空位置才能完成的任务，称为空间众包（Spatial Crowdsourcing，SC）。空间众包指以时空数据管理平台为基础，将具有时空特性的众包任务分配给非特定的众包参与者，要求众包参与者在一定约束条件下完成任务的一种新型众包计算模式［1］。共享经济和互联网的广泛应用使近年来各类O2O（Online To Offline）应用都采用了空间众包技术来提高其服务质量，如交通运输、电商平台、各类社交平台和自然灾害防控等。空间众包应用广泛，遍及衣食住行等各领域，如滴滴打车、美团外卖、饿了么等平台。随着终端硬件、数据分析技术和优化算法的不断发展和升级，空间众包应用将会扮演着越来越重要的角色［2］。如新冠肺炎此类传染疫情防控期间，人们可以通过空间众包平台实现多项社会服务，避免人员聚集，对疫情防控具有积极作用。

任务分配是空间众包研究领域核心问题之一，近年来，国内外学者围绕这一刚兴起的问题做了积极研究。空间众包任务分配基础研究包括空间众包任务和空间众包工作者两个角色，任务包含空间位置、发布时间、截止时间、任务回报等属性，工作者包括空间位置、是否在线、服务范围等属性［1-2］，研究目标主要是如何将任务分配给较近的工作者，使得差旅总成本最小、总效用最大或者总时间最小［3-5］。随着空间众包任务分配研究的进一步深入，更多不同的约束条件和研究目标被考虑。文献［6］中研究用户、工作者和工作点三种角色，提出自适应阈值算法并用于3 类对象的动态分配，并提出用竞争比指标来进行算法评价。文献［7］在文献［6］基础上，从离线预测和在线匹配角度提供一种在线三位稳定匹配，用不同匹配对应的工作者总收益来进行评价；文献［8］在同时满足众包参与者的距离、技能和截止时间等多个条件约束下进行任务分配，提出了基于贪心、分治和成本模型的启发式算法，并以最大化总收益为研究目标，以总收益函数为评价函数。文献［9］中研究了空间众包分配中给定时段的可选择人数上限和给定全部时段可选人数上限，讨论任务分配时工作者的及时覆盖率和最大化任务分配数，用覆盖率作为评价函数。文献［10］中提出以众包任务为核心的K近邻查询方法进行众包工作者候选，并基于动态效用阈值来过滤选择，尽量提高服务质量较高工作者的服务率。现有研究主要以总差旅成本、总覆盖率或工作者总收益为研究目标，考虑了距离、时间窗和技能匹配等约束，但是未考虑到用户存在各类偏好和用户满意等因素，然而生活中用户是否满意对各类空间众包平台的最终使用和普及有重要影响。

空间众包任务分配算法主要为贪婪算法。如文献［6-7］中均使用贪婪算法计算3 类对象的动态效用。文献［11］中将在线最大加权二部匹配问题的最新算法扩展到全局在线微任务分配，并提出二阶段框架，使用贪婪算法计算。文献［12］中以实时专车类服务为例，令所有乘客在订单被分配后至专车抵达期间的等待时间之和最小，研究了动态在线最小化二分图权值和匹配模型，通过实验说明贪心算法求解该模型具有很好效果。除贪婪算法外，文献［3］中用禁忌算法计算任务分配的总移动成本。文献［13］中尝试应用随机优化强化学习方法，并将司机接受任务的起始位置作为马尔可夫模型，研究多任务分配方法。文献［14］中提出多轮线性权值优化和粒子群优化算法，用于解决异构空间内任务分配覆盖率最大化。贪婪算法更适用于在线即时分配，强化学习适合复杂多变环境下的交互场景，上述算法能在不同场景中使用，但贪婪算法效率较低，强化学习训练模型需要较长时间。群智能算法更适合较多任务和工作者匹配组合求解，计算效率高，且不需要训练模型。

群智能优化算法是受生物群体间智能协作启发的算法，近年来不少学者利用群智能优化算法作为各类优化问题特别是调度、旅行商问题（Traveling Salesman Problem，TSP）等组合问题求最优解的方法。群智能优化算法主要包括粒子群算法［14-15］、遗传算法［16］、人工鱼群算法［17］和萤火虫群优化（Glowworm Swarm Optimization，GSO）算法［18-19］等。各类群智能优化算法都有各自优缺点。遗传算法应用广泛，具有较强鲁棒性，但是收敛容易过早且效率通常较低；粒子群算法搜索效率高，但是对于较高维数据寻优，非常容易陷入局部最优；人工鱼群算法鲁棒性强，初始条件和参数设定对它影响不大，所以适用范围大，但是收敛速度较慢；GSO 算法运算速度较快，在多维空间有较好寻优能力。虽然国内外学者通过从初始化、变步长、离散化、改变移动策略等方式［20-25］进一步优化算法性能，但是也存在一些不足：一方面，目前很少有基于改进GSO 算法来解决空间众包任务分配的研究；另一方面，改进算法的收敛速度和全局寻优能力有待进一步提升。本文算法将应用多种改进策略，并结合空间众包任务分配实际应用进行适合的有效编码，从而快速有效解决任务分配问题。

本文主要工作如下：1）定义了由用户偏好效用、延时等待效用和任务完成期望组成的用户满意效用概念，构建了基于用户满意效用的空间众包的任务分配（Spatial Crowdsourcing Task Allocation based on user Satisfaction utility，SSCTA）模型；2）提出了一种适用分配模型的改进离散萤火虫群优化（Improved discrete Glowworm Swarm Optimization，IGSO）算法；3）提出了使用IGSO 算法计算的任务分配方法IGSO-SSCTA（SSCTA based on IGSO）。与其他算法对比的实验结果表明，所提算法有更优的性能和适用性；对比其他任务分配策略，IGSO-SSCTA 具有更高的用户满意效用。

1 SSCTA模型

空间众包分配模型主要考虑空间众包任务和空间众包工作者两个主要概念。本文研究O2O 应用的“实时叫车”专车类空间众包任务分配。根据本文研究场景与模型的实际需要，创建并引入时空单位、用户偏好效用、延时等待效用和用户满意效用等四个概念，对任务与工作者两个概念的内涵进行了扩充。

1.1 SSCTA模型定义

研究场景假设模型符合以下前提条件：1）在线空间众包工作者才有可能接收到任务；2）空间众包工作者正在完成任务过程中无法接收新任务；3）服务器在分配任务时，除了考虑用户延时等待的时间（越短越好），还需考虑工作者（包含车辆，以下统一用工作者表示）和用户偏好的匹配程度（越大越好）；4）用户发布任务后，截止时间为用户自主取消任务时，服务器只考虑当前线上存在的任务。

模型相关概念定义如下：

定义1空间众包任务［1］。用户偏好空间众包任务u=其中lu为任务u的初始位置，tu为用户发布任务的时间标签，su为任务u当前是否正在发布，pu为用户的各项偏好情况。

定义2空间众包工作者［1］。空间众包工作者w=其中lw为工作者w的当前位置，tw为工作者不同位置的时间标签，sw为工作者的当前状态（是否在线、是否正在完成任务等），qw为工作者在用户偏好各项指标下得分，zw为工作者历史任务完成的成功率。

定义3时空单位。将研究区域等分成N个面积为R的正方形，某一时间戳T内的每一个正方形组成一个时空单位K，K=R×T。

定义4用户偏好效用。指工作者和用户在用户偏好下的匹配程度。设用户偏好权重系数为pu，工作者在该用户偏好对应的得分为qw，用户偏好效用为huw，用户有K个偏好，用户u和工作者w匹配的用户偏好效用定义为huw=

定义5延时等待效用。延时等待时间是用户从发出任务申请到工作者到达用户任务位置等待的总时间，延时等待时间越大，效用越小。等待总时间由系统分配任务时间ts和工作者实际旅行时间tuw两部分组成。设用户和工作者距离为luw，工作者速度为vw，则tuw=luw/vw。等待时间为0 时效用最高，将此时的等待效用设为d0，假设系统分配时间为常数t0，用户的延时等待效用为duw，满足函数duw(t)=f(tuw+t0)。

定义6用户满意效用。用来描述用户满意程度的高低，用suw表示，由用户偏好效用和延时等待效用、任务完成期望组成。任务完成期望由对应的工作者历史任务成功率zw决定，故suw=zw× (r1×huw+r2×duw)，r1、r2为用户偏好效用和延时等待效用系数，是两部分效用在用户满意效用中重要度。

1.2 SSCTA模型设计和构建

1.2.1 用户偏好指标调查和设计

通过随机抽样共发放500 份问卷（收回问卷495份，其中有效问卷490 份），问卷主要内容是调研用户偏好的指标及用户对延时等待的阈值接受程度，通过与20 位调查对象深度访谈与头脑风暴产生。调查过程是对合肥市商业区和住宅区等人员密集的地区随机采样，人群年龄分布为20 岁以下占26.8%，20～50 岁占70.3%，50 岁以上占2.9%。用户偏好设置为多选。统计发现用户对遵守交通规则、车内卫生、驾驶平稳、文明礼仪、路况熟悉度、车辆品质等六个方面最为重视，其次还有用户对工作者性别、车内是否有烟味等方面提出偏好要求，具体如表1 所示。

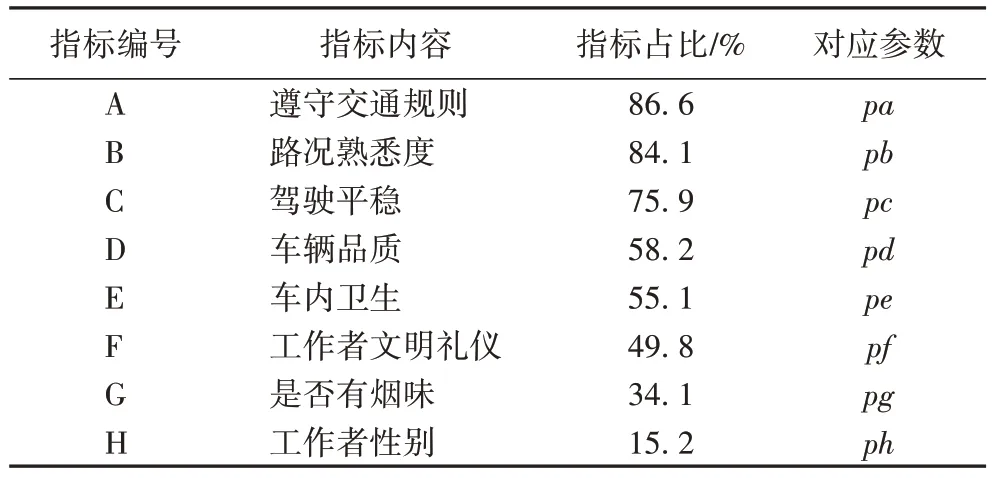
表1 用户偏好指标Tab.1 Indicators of user preferences

每一项指标得分均为百分制。其中，A、B、C、D 一般由系统根据工作者的实时数据和历史数据系统给予综合评价，取值范围是［0，100］；E、F、G 由各用户在任务完成后对该工作者评价，取值范围也是［0，100］；工作者性别指标主要从安全角度考虑，如女性用户在夜晚出行时，倾向女性工作者，取值为0 或者100，性别符合为100，否则为0。

1.2.2 用户延时等待效用函数

问卷还针对用户等待时间，以0 s～100 s、100 s～300 s、大于300 s 分段进行了调查。调查发现82%以上用户对从发出任务申请到系统指派工作者到达任务地点的理想等待时间在100 s 内（含系统分配任务时间，分配任务理想时间为20 s），75%以上用户认为可接受最长等待时间为300 s，超过300 s 较难接受。100 s 是用户体验重要界限，100 s 内用户延时等待效用逐渐缓慢降低，100 s 到300 s 之间用户延时等待效用较快下降。300 s 后延时等待效用较小，降低也较慢。综上，将用户的延时等待效用函数设计为分段函数，取值范围是（0，100），具体如下，其中，tuw=luw/vw，详见定义5。

1.2.3 SSCTA模型构建

假设某时空单位下，有n个用户和m个工作者，每个用户都有K种偏好，m≤n，则一次任务分配中共有种工作者和用户会匹配，每种匹配又分别有m！种 组合，这种组合匹配方式和计算量的复杂度，与经典旅行商问题相当［26-27］，属于NP（Non-deterministic Polynomial）-Hard 问题。构建模型和对应约束规划条件具体如下：

在上述模型中，式（2）表示求一次任务分配中所有用户和工作者匹配组合的用户满意效用总和的最大值；式（3）～（9）分别表示总用户满意效用、每一对工作者与用户的用户偏好效用、延时等待效用、等待时间、工作者集合、工作者匹配对应的用户集合、用户偏好的集合等。

2 IGSO-SSCTA任务分配方法

萤火虫算法共有GSO 算法［18］和FA（Firefly Algorithm）［19］两种，原理相似，都是受萤火虫群个体间移动的仿生过程启发而设计，本文选择萤火虫群优化（GSO）算法［18］进行改进。

2.1 GSO算法原理

萤火虫的荧光素对应目标函数，荧光素越大萤火虫越亮，吸引力更强，吸引能力随距离增加而较小。GSO 共有荧光素更新、选择移动方向、位置更新、决策域更新等阶段，具体步骤如下：

其中：li(t) 是萤火虫的荧光素值；ρ是萤火素挥发系数；γ、J(xi(t))分别指荧光素的增强系数和第t次迭代时的目标函数值；Ni(t)是萤火虫xi在决策域内第t次迭代时比它更亮的萤火虫个体组成的集合；ρij(t)指当前萤火虫xi移向更亮萤火虫xj的概率；s是步长，β为感知半径的系数；nt为邻域萤火虫数量阈值；rs为邻阈感知半径。

萤火虫群算法面向连续空间，在解决组合问题实际应用时，需要离散化处理。离散化通常有两种方法：一种是通过初始离散值构建、离散编码和编码更新规则［18-19］，让算法能按照原始寻优方式始终运行在离散空间；另一种是将连续空间的解按概率映射到指定离散解空间。第一种方法更适合本文模型求解。

2.2 IGSO-SSCTA方法整体方案

2.2.1 目标函数

根据SSCTA 模型，通过构建惩罚函数的方式，用加权线性函数将多目标转化为单目标问题，再使用算法求解。目标函数构建如下，其中c1、c2为用户偏好效用和延时等待效用的量纲调节系数，确保两类数据在同一量纲级别，r1、r2参看定义6。

2.2.2 改进离散萤火虫群优化算法

为解决本文场景下空间众包任务分配中的组合匹配寻优问题，根据应用实际和需求，对萤火虫算法进行对应改进，求解实际问题。

1）编码和解码。

初始解按照编码规则随机生成，每一维度的下标表示工作者编号，每一维度上数字表示用户编号，第a位上的数字b代表用户b与工作者a组合。如第2 维度上是5，就代表用户5 与工作者2 组合。下标顺序固定不变，即工作者顺序不变，用户排序不断变化，从而实现用户和工作者各种组合匹配。

2）反向学习协同初始化。

反向学习［28］主要是检测种群某时刻算法下的历史较差解，根据反向数生成反向解将其代替，优化种群整体位置［29］。设R上存在d维空间离散点xi=[m，n]，i∈{1，2，…，d}，则x在i维的反向数定义为：

反向学习协同初始化种群，指初始化种群时，种群按照目标函数排序，排序在前一半的种群保持不变，排序在后一半的种群采用反向学习策略，最后两部分种群组成新的种群，相较于随机生成的初始种群有更好的解空间。

3）距离计算。

萤火虫i与萤火虫j使用海明距离，如果第g维上数值相同，则记为0；否则记为1。每条萤火虫各维上的距离总和即为两条萤火虫的实际距离，详见式（17）～（18）：

其中：g∈[1，m]。

4）四种改进的移动策略。

根据移动规则，萤火虫之间寻优移动会导致一只萤火虫上不同维度上的值相同，即产生不可行解。为了保证解有应用价值，离散萤火虫群算法步长应为当前离散萤火虫每一维度编码向移动萤火虫同一维度编码趋同的变化概率，且始终要保证不同维度上的解不能重复。在算法迭代中，以变异因子R引入四种移动策略，这四种移动策略可以保证移动后的解仍然是可行解，包括互交换变异［30］、反演变异［30］、左相邻交换、右相邻交换。

以上四种移动策略在确保解有应用价值的前提下，能有效增加萤火虫移动，避免萤火虫陷入局部最优。四种改进移动策略均假设第2 维和第5 维的（4，1）发生移动，具体移动过程详见表2。互交换移动指两个维度上的值进行交换，如第2 维和第5 维的（4，1）变为（1，4）；反演指第2 维和第5 维之间的（4，6，8，1）均和对称位置上的值发生交换，变为（1，8，6，4）；左相邻交换即和左边相邻的维度上的值发生交换，如4和3 交换、1 和2 交换；右相邻交换以此类推，和右边相邻的维度上的值发生交换。

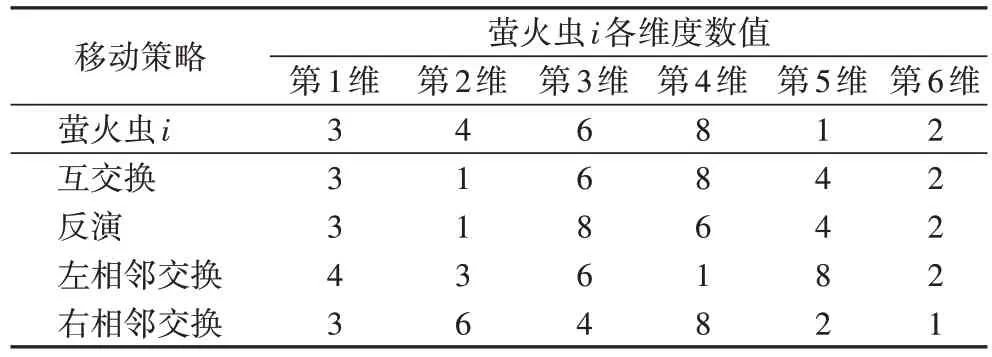
表2 四种移动策略Tab.2 Four mobile strategies

5）移动策略的自适应选择。

为针对不同迭代阶段，更好地从四种不同移动策略中选择最适宜的移动策略，提高收敛速度和寻优质量，引入自适应选择方法［31］，具体如下：其中：qg(t+1)表示第g种移动策略的近期表现；h为适应率，h∈(0，1)；rg(t)表示第g种移动方式在t代的贡献。G表示四种移动策略集合，pg(t)表示第g种移动方式在t代的选择概率。pmin表示移动策略的最小选择概率，为常数。为了不降低算法的收敛速度，每迭代20 次更新1 次选择概率，移动方式g对应的采用概率如下式：

6）不可行解处理。

萤火虫i为xi(t)={1，3，4，9，2}，邻域更亮萤火虫c为xc(t)={3，4，5，7，6}，假设移动后萤火虫i的第1、3 维和萤火虫中心位置趋同，此时xi(t+1)={3，3，5，9，2}。该解表示1号和2 号工作者同时为3 号用户服务，这不符合场景应用的前提条件，为不可行解。用以下方式处理：向萤火虫中心c趋同的位置集合（1，3），这两个维度作为寻优移动后变化得到的位置应保留，更新后萤火虫i编码重复的位置为（1，2）。将第2 维上随机生成不重复且在有效解空间内的编码。经以上处理可能产生的一个解是xi(t+1)={3，7，5，9，2}，具备应用价值。由于编码规则和解空间的限制，按照此种方法和规则产生的其他解也均会是可行解。

2.2.3 IGSO-SSCTA方法流程和步骤

IGSO-SSCTA 方法步骤由SSCTA 模型和IGSO 算法两部分组成，具体步骤如下：

步骤1 将交通数据预处理，通过无量纲化归一化处理，将其映射到指定空间内。

步骤2 将给定时空划分成N个时空单元，将每个时空单元的用户与工作者编号。

步骤3 按照编码规则，采用反向学习协同初始化萤火虫群，更新种群荧光素。

步骤4 萤火虫群在变异因子参数下向邻域内最亮的萤火虫移动或者按照自适应选择四种改进策略移动。

步骤5 对不可行解进行检查和处理。

步骤6 将目标函数值与公告板对比，如果没有公告板更优，则公告板不变；反之，取代公告板数值。

步骤7 检查是否达到终止条件（达到迭代数或达到用户满意效用要求），达到条件后输出用户满意效用较好的任务分配组合。

2.2.4 时空复杂度分析

设种群规模为n，用户与工作者组合数为m，用户偏好指标数量为p，每只萤火虫（m维）代表一种组合，最大迭代数为T。

算法时间复杂度分析：初始化萤火虫种群时间复杂度为O（n），计算一对用户与工作者匹配的效用时间复杂度O（m*p），故每一次迭代中计算任务分配总效用时间复杂度O（n*m*p）；每次迭代中计算萤火虫个体间距离的时间复杂度为O（m）；每次迭代中计算萤火虫个体移动的时间复杂度为O（n*m）；每次迭代中计算萤火虫种群位置更新的时间复杂度为O（n2*m）；因此离散型萤火虫算法时间复杂度为O（n2*m*T）（实际应用中，通常n＞p）。

算法空间复杂度分析：初始化离散萤火虫种群和参数空间复杂度为O（n*m）；计算萤火虫个体间距离的空间复杂度为O（n*m）；计算萤火虫个体位置更新的空间复杂度为O（m*p）；萤火虫群位置更新的空间复杂度为O（n*m*p）；所以，该离散型萤火虫算法空间复杂度为O（n*m*p）。

3 实验与结果分析

3.1 实验环境和参数

实验在Matlab R2016a 中完成，计算机参数：系统Windows7、内存8 GB，CPU Intel Core i5-4460 3.2 GHz。

参照文献［18，30］，结合算法参数实验，本文算法参数设置如下：初始种群规模n设置为20，最大迭代次数t设置为200（本文算法t=100 时已趋于稳定，为了对比其他算法，t取200）。本文所有对比实验均取20 次独立重复实验的平均值作为对比数据。因为用户偏好和延时等待均需要考虑，假设两方面对用户同等重要，r1=0.5，r2=0.5。设定模拟用户满意效用和延时等待效用的最大值均为100，经实验计算，两类数据取值在同一量纲范围，取c1=1，c2=1。对比算法中，除表3 中的参数，其他未提及的参数或其他算法中各类参数，均使用原文默认参数，以保持对比算法性能。

由于贪婪算法是目前空间众包任务分配的常用算法［6-7］，有学者使用基于随机阈值的改进贪婪算法（Greedy algorithm based on Random threshold，GR）［6］取得较好效果。MGSO（Modified Glowworm Swarm Optimization）算法［24］、FGSO（Fire Glowworm Swarm Optimization）算法［25］和本文一样，都是在GSO 算法上改进的较新算法，按同样方式进行初始编码。本文引入时空单元将动态任务分配转化为静态场景的组合问题，前文分析该组合问题近似TSP，所以TSP 相关算法可以计 算 SSCTA模型 。IDFA（Improved Discrete Firefly Algorithm）［26］和CDFA（Change Based on Firefly Algorithm）［27］是基于另一种萤火虫算法改进解决组合问题取得良好效果的算法。此外，为了对比反向学习初始化策略对改进的影响，将本文IGSO 算法初始化策略删除后得到DGSO（Discrete Glowworm Swarm Optimization）算法。综上，详见表3 所有算法。

表3 不同算法的主要参数Tab.3 Main parameters of different algorithms

3.2 IGSO-SSCTA方法实验

3.2.1 实验数据来源

实验数据包含用户偏好、位置、速度、工作者得分、时间、工作者任务完成成功率等，其中，位置数据是在聚数力网站（http：//dataju.cn）［32］下载，删除重复位置信息后，得到实验所需3 000 个任务地理位置坐标，按比例映射到［0，100］，其他数据通过实际调查和随机产生，具体如表4 所示。其中，考虑实际生活中，每个用户各侧重偏好均不一致，假设每个用户存在1～2 种偏好。如果是一种偏好，则系数为1；如果存在两种偏好，则两种偏好系数和为1。该项数据为随机生成。

表4 实验数据说明Tab.4 Experimental data explanation

3.2.2 小规模数据实验说明

1）不同策略用户满意效用对比。

根据表4 实验数据来源方式，假设同一空间单元连续12个时间戳组成的时空单位K1～K12依次发生M1中12 种规模的任务分配，合成12 组小规模数据集Sdate1～Sdate12。分别用四种策略计算任务分配的用户满意效用：第一种是IGSO-SSCTA，结果记为P（S）；第二种是考虑距离成本的任务分配［3］，结果记为P（L）；第三种考虑时间总和最小的任务分配［12］，结果记为P（T）；第四种是随机分配，结果记为P（R）。针对每个数据集分别做20 次独立实验。

实验结果见表5，包含20 次实验结果的最大值MAX、最小值MIN 和平均值AVG。12 组数据集上实验平均值显示，IGSO-SSCTA 方法不受用户与工作者的位置影响，在12 组数据集上，P（S）模式用户满意效用总是最优。综合12 组数据集的平均结果，P（S）相较于P（T）、P（L）和P（R）分别提升了9.64%、11.77%、15.70%。这说明IGSO-SSCTA 方法在小规模数据集上任务分配的用户满意效用有显著提升，针对不同数据集有广泛的适用性。P（R）策略用户满意效用最低，P（T）比P（L）均要高，这说明等待时间比路程长路在用户满意效用上影响更直接。静态视角下，将Sdate1～Sdate12对应K1～K12的用户满意效用，由于K1～K12是同一空间的12 个连续时间戳，所以Sdate1～Sdate12实验结果可直接相加。这种时空分割方法提供了静态任务分配转化动态任务分配的一种策略。

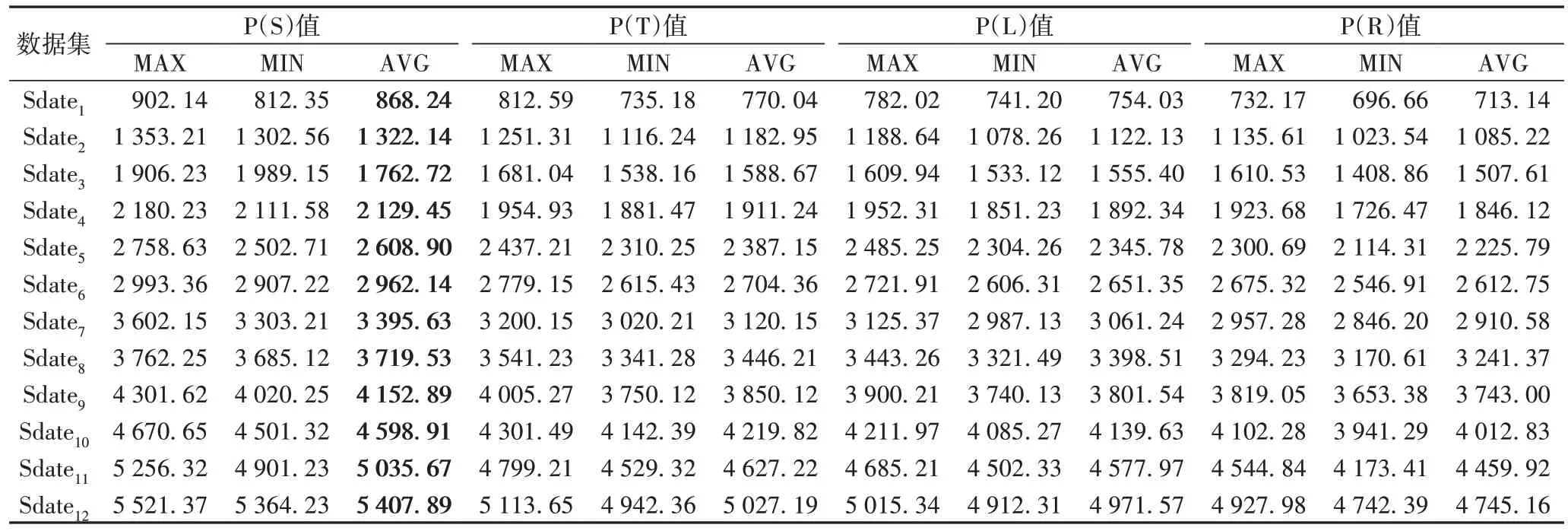
表5 四种策略的用户满意效用对比Tab.5 User satisfaction utility comparison of four strategies

2）不同算法计算结果对比。

选择表3 中的7 种算法来进行性能测试对比，重复20 次实验得到图1。7 种算法均在初始化时使用同样编码方式，均使用自身算法迭代更新和求解方式，种群均为20。根据目标函数迭代200 次平均结果，得到图1。

从整体结果看，IGSO 在12 组数据集上最终求解均优于其他算法；DGSO 算法整体上弱于IGSO 算法，但强于其他算法；GR 求解结果明显弱于其他算法；IDFA、CDFA、MGSO 和FGSO 算法计算结果较为接近。这说明IGSO 有较好的寻优能力，因为算法增加了四种移动策略。DGSO 在Sdate1、Sdate4和Sdate6和IGSO 求解结果很接近，在其他数据集上略低于IGSO，这说明反向学习初始化在一定程度上可以提高算法寻优效率。GR 随着数据集规模增大，求解结果相较于其他算法差距越来越大。IDFA、CDFA、MGSO 和FGSO 算法在不同数据集上求解结果各有优劣，这说明适用性不同，侧面说明了IGSO 算法的稳定性。从寻优速度看，在初始化到迭代20 次内，IGSO 寻优效率高于其他算法，而IGSO 与DGSO 寻优策略相同，这说明反向学习协同初始化提高了初始解的质量，所以提高了寻优效率。当迭代运行到100 次后，所有算法趋于稳定，IGSO 计算结果仍然优于其他算法。

综上，IGSO 算法结果相比较其他6 种算法，收敛更快，求得平均结果更优。

3）不同算法寻优时间对比。

根据7 种算法20 次重复实验消耗的平均时间，得到表6。

表6 不同算法的求解时间 单位：sTab.6 Solution times of different algorithms unit：s

IGSO 比MGSO、FGSO、IDFA 耗时短，原因是使用了自适应选择的四种移动策略，多种寻优策略一定程度上减小了求解时间。在Sdate1～Sdate12上随着数据集规模增大，7 种算法寻优求解时间有小幅度增加，GR 寻优时间显著增长。DGSO算法在Sdate1～Sdate3上求解时间略低于IGSO算法，在Sdate4～Sdate12高于IGSO 算法，这说明反向学习会耗用时间；但随着数据集规模增大，IGSO 耗时比DGSO 更短，这说明反向学习会产生更优的初始解，提高了后期寻优的效率，所以缩短了总时间。因为7 种算法种群等主要参数相同，由此可见IGSO 收敛较快，寻优速度快，IGSO、IDFA 和CDFA 相较于GR，更适用规模较大数据集。

3.2.3 较大规模数据实验说明

当m分别取M2中的6 组较大规模数据集时，重复20 次独立实验，平均结果见表7。在不同规模数据集计算结果中，IGSO 始终比其他对比算法要更高，IDFA 和CDFA 互有高低，始终优于GR。综合对比，IGSO 在较大规模数据集上仍然有更好的求解能力，说明算法稳定性较好。

表7 七种算法在M2上的求解结果Tab.7 Results of seven algorithms on M2

从小规模数据集M1及较大规模数据集M2的实验可以看出，IGSO-SSCTA 相较于其他算法能较好地适用于各种规模的数据集。在实际应用场景下，m的取值理论上是任意正整数，而每一次分配都是在时空单位下相应的工作者和用户完成匹配组合，所以分割适宜大小的时空单元K，从而控制m的规模，保证IGSO-SSCTA 有较好的计算效率和稳定性。

3.3 IGSO算法参数调试

IGSO 算法主要参数包括种群规模、感知半径、邻域阈值和变异因子。其中，从上述7 种算法性能对比实验中可以得知迭代次数到200前，IGSO 算法结果均趋于稳定，为测试其他参数对算法性能影响，以Sdate1为实验数据集，重复独立实验20 次取平均值，得到图2。

IGSO 算法计算的用户满意效用随种群规模变大而递增，直到种群规模达到20，用户满意效用趋于稳定；用户满意效用随着邻域阈值的增大不断波动，在邻域阈值取6 时取得最佳值；用户满意效用随着感知距离的增大，计算结果先降低再升高最后又降低，在15 时达到最大值；算法随变异因子取值变化计算结果也一直波动，变异因子取0.4 时算法性能最优，这说明算法的四种移动策略在改善算法求解性能方便有较显著的提升作用。通过参数实验，种群规模取20，邻域阈值取6，感知距离取15，变异因子取0.4。

4 结语

针对生活中专车类空间众包平台不关注用户存在偏好和延时等待的现状，为了进一步提高用户满意效用，本文提出了基于用户满意效用的空间众包任务分配方法IGSOSSCTA。与其他方法对比，该方法能显著提高用户满意效用。改进的离散萤火虫群优化算法IGSO 与其他算法在不同规模数据集上的实验对比结果表明，IGSO 在该空间众包任务分配应用中有更好的适用性、稳定性和收敛性。下一步将围绕激励工作者角度，研究在隐私保护前提下，如何提高专车类空间众包工作者的服务质量和积极性。