地磁感应电流研究综述

步宛烨，张慧茜，黄清华,2*

1北京大学地球与空间科学学院地球物理学系，北京100871

2河北红山地球物理国家野外科学观测研究站，北京大学，北京100871

0 引言

太阳活动所引起的地磁扰动会在地球表面引起感生地电场，从而在地面导体系统中产生低频电流，称为地磁感应电流（geomagnetically induced currents,GICs）.

GICs作为造成空间天气灾害的重要因素之一，会对导体设施产生威胁.早在一个多世纪前，人类就观测到了GICs对电报通信系统的影响（Barlow,1849）.1859年9月1日至2日观测到的卡林顿超级磁暴（Carrington,1859），甚至曾导致电报线起火（Boteler,2006）.除了干扰通信系统，GICs还能腐蚀油气管道，给油气运输带来长期的潜在威胁（Allison and Huddleston,1952;Pulkkinen et al.,2001）.GICs也会影响轨道的自动控制系统，对铁路系统产生危害.例如，1982年7月，瑞典铁路的轨道电路受到GICs的影响而出现信号灯“闪红”现象（Wik et al.,2009）.1989年3月的磁暴使前苏联Gorky铁路的信号控制系统出现了异常（Eroshenko et al.,2010）.随着电力系统的不断发展，电网系统成为受GICs影响最大的导体系统.早在1940年，美国和加拿大电网受GICs干扰的现象就 已 被 发 现（Davidson,1940; McNish,1940）.1989年3月13日，在强GICs的干扰下，加拿大魁北克省的电力系统出现大范围的电压崩溃，约600万人持续断电9个小时. 美国新泽西州的一个发电机的升压变压器也在该事件中被烧毁（Allen et al., 1989;Boteler, 2001;Bolduc,2002）.

事实上，GICs甚至可以造成更大程度的灾害.1859年的卡林顿级别的超级磁暴，是1989年导致魁北克断电的磁暴强度的1.5倍（Siscoe et al.,2006）.如果卡林顿级别的磁暴发生在导体系统高度发达的今天，可能会引起难以预估的后果（Kelbert,2020）.2012年7月23日发生过一次强太阳活动事件，如果该事件袭击地球，引起的感应地电场强度甚至可能会超过1989年的磁暴（Ngwira et al.,2013）.基于概率估计的研究也表明卡林顿级别的地磁暴存在重复发生的可能，例如，Riley（2012）基于幂律分布得出结论：卡林顿磁暴事件（Dst<−850 nT）在未来10年内发生的概率约为12%. 因此，为了提前预警并规避极端GICs的危害，研究其产生原理和机制是非常必要的.

在早期，研究者们普遍认为只有高纬度地区会遭受GICs的灾害，比如加拿大（Boteler,2001）、瑞典（Wik et al.,2008,2009）、芬兰（Pirjola et al.,2007）等，因此早期的GICs研究主要集中在高纬度区域.然而，随着电力系统的发展，在中低纬度地区也出现了GICs影响电网的事件，比如中国（刘连光等，2008）、南非（Koen and Guant,2003）、西班牙（Torta et al.,2012）和新西兰（Béland and Small,2004）.因此GICs研究在低纬度地区也开始发展，比如中国（Liu et al.,2009;Zhang et al.,2015,2020）、日本（Watari et al.,2009;Watari, 2015）、新 西 兰（Marshall et al.,2012;Divett et al.,2017,2018）、巴西（Trivedi et al.,2007;Barbosa et al.,2015）、南非（Matandirotya et al.,2015,2016;Lotz and Danskin,2017）、澳大利亚（Marshall et al.,2019,2020）和西班牙（Torta et al.,2012,2014,2017）等.

本文将对GICs的研究进行概述.首先简述空间天气对GICs的驱动原理，然后分别介绍计算GICs的三个步骤的相关原理和研究进展，包括地球表面地磁场的重建，感应地电场的计算，以及地面导体系统中GICs的计算.最后对当前GICs的研究方向加以总结，并对其未来研究提出展望.

1 驱动GICs的空间天气链

空间天气这一概念首次出现于1950年代，并在1990年代普遍使用（Cade and Chan-Park,2015）.空间天气是指由太阳内部、太阳大气、太阳风以及地球磁层、电离层和热层组成的复杂系统的物理条件（Abda et al.,2020）.从空间天气的角度，GICs实际上是太阳—太阳风—磁层—电离层—地球这一空间天气链在地表的最终体现（Pulkkinen et al.,2017），如图1所示.

图1 地磁感应电流的“太阳—太阳风—磁层—电离层—地球”空间天气链（修改自Abda et al.,2020）Fig.1 The"sun-solar wind-magnetosphere-ionosphere-earth"space weather chain of geomagnetic induced currents(modified from Abda et al.,2020)

近几十年来，人们对太阳、太阳风、磁层、电离层以及固体地球，特别是它们之间的耦合关系的认识取得了重大进展，因而对驱动GICs的关键过程的了解也日趋成熟（Pulkkinen et al.,2017）.剧烈的太阳活动，例如太阳黑子、耀斑爆发、日冕物质抛射（CME）等，会导致大量等离子体喷出，并且形成携带着巨大能量的太阳风.当太阳风高速运动并传播到地球附近后，会与地球磁场发生复杂的相互作用，从而影响磁层以及电离层内的物理过程，并产生一系列电流体系.这些电流源驱动了地球表面的电磁感应现象，从而导致地磁扰动，形成地磁暴. 时变的磁场会在地表感应出地电场，进而在导体系统中产生GICs（刘春明,2009;Abda et al.,2020）.

地磁感应电流是由地球表面的地磁扰动直接驱动的，因而GICs的计算通常从地磁场出发，首先根据地磁观测或空间天气参数重建地球表面的地磁场，然后根据大地电导率结构计算地表的感应地电场，最终基于导体系统的参数和结构计算其中流动的GICs.下面将分别介绍GICs计算的三个步骤的相关原理和发展.

2 地磁场的重建

2.1 地磁场的地面观测和插值

计算GICs的第一步是重建地球表面的地磁场.要获得地面总地磁场变化的信息，最直接的方法就是地面观测.人类对地磁场的观测已经开展了一个多世纪.目前，很多国家都布设了长期的地磁台站，形成了全球覆盖的地磁观测网.但是，地磁观测台站的数目在全球范围内依旧稀少，并且分布不均，有些台站的记录也有所缺失，需要通过地球物理的方法对其在空间上进行插值.

最常用的地磁记录插值方法是Amm和Viljanen（1999）提出的SECS（spherical elementary current systems）方法，该方法利用电离层电流中的无旋分量（不影响地球表面磁场，因而可被忽略）这一性质，将无散分量作为等效电流，根据已知的地磁场观测数据，计算无散的等效电离层电流分布，如图2所示.而基于毕奥—萨伐尔定律，如果能确定磁层和电离层的电流体系，就可以准确地计算出地面上相应的外部地磁场的变化（Rastätter et al.,2014）.相比于传统的傅里叶变换、球谐分析法和球冠谐分析法，SECS方法不需要对频谱进行截断，并且可以任意设置等效电流系统的位置以适应地磁测点的分布和所要研究问题的电流体系（Amm and Viljanen,1999）.目前大部分运用地磁观测数据来计算GICs的研究都是采用SECS方法进行插值（例如，Caraballo et al.,2020;Lucas et al.,2020;Wang et al.,2020;Alves Ribeiro et al.,2021）.

图2 SECS示意图.（a）无旋的电流体系（与相关的场向电流）；（b）无散的电流体系（修改自Amm and Viljanen,1999）Fig.2 Sketch of spherical elementary current systems(SECS).(a)Curl-free elementary system(with associated FACs);(b)Divergence-free elementary system(modified from Amm and Viljanen,1999).

2.2 基于空间天气的地磁场模拟

除了地面观测的方式，地球表面的地磁场还可以根据第一性原理，采用全球三维磁流体力学（magnetohydrodynamics, MHD）模型，根据空间天气参数来模拟（Pulkkinen et al.,2013;Glocer et al.,2016）.基于太阳风和行星际磁场等参数，利用结合流体力学方程和麦克斯韦方程组而得到的MHD模型，可以直接预测磁层和电离层的电流体系，进而计算地表磁场的扰动情况.比较常用的MHD模型有BATS-R-US（the block-adaptive-treesolarwind-roe-upwind-scheme）模型（Powell et al.,1999）、GUMICS（grand unified ionospheremagnetosphere coupling simuation）模型（Palmroth et al.,2001）、OpenGGCM（open geospace general circulation model）模型（Raeder et al.,2001）、LFM（the lyon–fedder–mobarry）模型（Lyon et al., 2004）、SWMF（space weather modeling framework）模型（Tóth et al.,2005）和PPMLR-MHD（lagrangian version of piecewise parabolic method-magnetohydrodynamic）模型（Hu et al.,2005）等.

目前已有很多GICs的相关研究利用MHD模型来计算地磁场变化.Pulkkinen等（2013）选取了12个地磁台站的数据，分别采用两种经验模型（Weimer和Weigel经验模型）以及三种MHD模型（LFM-MIX，OpenGGCM和SWMF模型），对6次地磁暴事件的地磁扰动进行预测，计算了地磁场的时间导数（dB/dt），并通过列联表评估各个模型的性能.Ngwira等（2014）利用全球三维MHD模型（SWMF模型）计算了卡林顿磁暴时的磁层—电离层响应以及地磁场和感应地电场.Zhang等（2020）利用SWMF模型与一维电导率模型，模拟了磁暴期间我国低纬度变电站的地磁扰动以及GICs. 模拟结果表明，该模型对Bx分量的拟合效果好于By分量.

尽管在这一领域已经取得了很多进展，但要准确地描述全球磁层和电离层电流的变化仍然非常有挑战性.驱动地电场的地磁扰动的时空差异性很大，外部电流体系的微小变化就可能导致对局部地磁场预测的较大误差，从而影响地电场和GICs的模拟（Ngwira et al.,2015;Pulkkinen et al., 2015,2017）.另外，某些物理现象，比如亚暴电流体系或赤道电射流等，无法用单一的理想MHD模型来描述（Ngwira et al.,2014）.同时，MHD方法依赖于对空间天气参数的观测，包括行星际磁场的三分量值、太阳风的速度、密度和温度等，因此未来更高精度的空间天气探测计划可能会有助于提高MHD模拟的精度.

3 感应地电场的计算

地电场是评估灾害和研究极端天气事件的重要参数，也是GICs研究的关键.在重建了地面地磁场以后，计算GICs的第二步是基于大地电阻率模型，通过重建的地磁场变化来计算地电场的时空变化.

3.1 基于平面波假设的地电场计算方法

几十年来，Cagniard（1953）提出的“平面波法”一直是计算感应地电场的基础方法. 该方法假设来自磁层—电离层源的磁场可以近似为平面波.根据法拉第电磁感应定律和麦克斯韦方程，地电场E可以表示成是通过地磁场B与大地阻抗张量Z在时域的卷积.经过傅里叶变换，可以转换为在频率域的乘积（Lucas et al.,2020）：

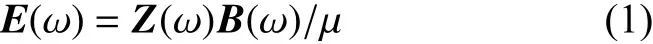
式中，µ是磁导率，E是水平地电场，B是水平地磁场，Z是大地阻抗张量.

目前应用最广泛的方法是一维平面波法，认为地球电导率分布可以近似为仅随深度变化的一维结构，从而采用一维半空间层状电导率结构模型来计算地表阻抗Z.

阻抗张量Z在一维情况下可以写为：

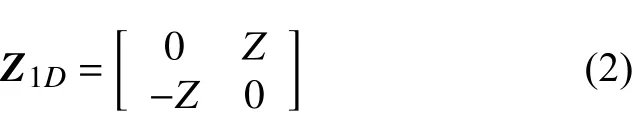
将Z1D代入公式（1）即可计算地电场的水平分量.

本文我们通过一些模拟来探究一维层状电导率结构和地磁暴频率对感应地电场的影响.假设地下电导率结构由两个厚度均为10 km的均匀层及底部的均匀半空间组成（图3）.取半空间电导率σ3=0.01 S/m保持不变，顶部两层电导率分别在0.000 1～1 S/m范围内变化，当改变某一层的电导率时，另一层电导率固定在0.01 S/m.

图3 三层大地电导率模型Fig.3 Three-layer earth conductivity model

我们取磁暴频率分别为0.01 Hz、0.001 Hz和0.000 1 Hz，并假设地磁场的By分量为500 nT，分别计算对应的地面地电场Ex分量的绝对值，结果如图4所示.

从图4可以看出，地电场会随任一层中电导率的增大而降低，并且高频磁场会感生出更大幅度的地电场. 因此，高频短周期的磁暴会在低电导率区域产生更强的地电灾害.同时，对比同一频率的计算结果，当两层电导率均在0.000 1～1 S/m范围内变化时，地电场值随着浅层电导率的变化更明显，因此浅层电导率对地电场的影响更大.随着频率的降低，两层的电导率对地电场的影响差异逐渐减小.因此，高频磁暴期间所造成的地电灾害主要受到浅层电导率的影响.

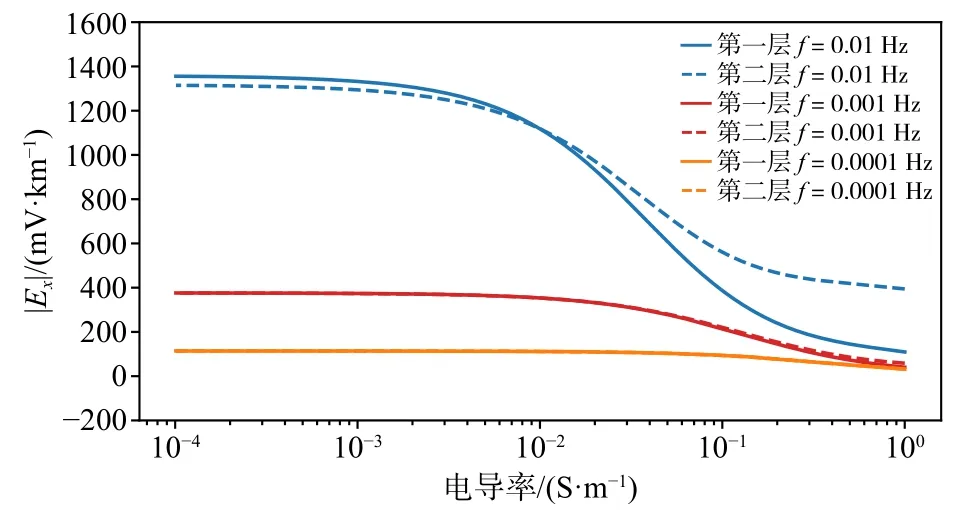
图4 地电场随第一、二层电导率以及频率的变化曲线.蓝线、红线和橘线的频率分别为0.01 Hz、0.001 Hz和0.000 1 Hz.实线表示随着第一层电导率变化时的地电场，虚线表示随着第二层电导率变化时的地电场Fig.4 The variation curves of the geoelectric field value with the conductivity and frequency of the first layer and the second layer.The blue, red and orange lines have frequencies of 0.01 Hz,0.001 Hz and 0.000 1 Hz,respectively.The solid lines show the geoelectric field as the conductivity of the first layer changes,and the dashed lines show the geoelectric field as the conductivity of the second layer changes

上述模拟中假定地表磁场是均匀的，但在实际情况下，基于麦克斯韦方程，大地电导率模型的区域性差异会导致感应地磁场的空间变化，因此利用均匀的地磁场来模拟磁暴在空间变化的电导率模型下的电磁响应会产生误差.为了探究电阻率模型的影响，我们考虑感应地磁场的影响，根据波的传播和衰减的特性，将地磁场和地电场看成是由入射波（Ei和Bi）和反射波（Er和Br）组成，将地磁场和地电场写成如下形式（李金铭，2005）：

基于上述公式，选用与图3同样的电阻率模型，取入射磁场By为500 nT，计算频率分别为0.01 Hz、0.001 Hz和0.000 1 Hz的地电场，如图5所示.

从图5可以看出，地电场依然保持着随电导率增大而降低的规律，并且地电场的幅值受到浅层电阻率的影响更大.同时，对比不同频率，高频磁场会感生出更大的地电场.因此，我们依旧得到了与方法一（不考虑感应场）相同的结论，即在一维层状介质和平面波假设下，高频磁暴和低电导率结构会导致更强的地电灾害，并且相对浅层的电导率结构对电场值的影响更大.

图5 考虑感应场时，地电场随第一、二层电导率以及频率的变化曲线.蓝线、红线和橘线的频率分别为0.01 Hz、0.001 Hz和0.000 1 Hz.实线表示随着第一层电导率变化时的地电场，虚线表示随着第二层电导率变化时的地电场Fig.5 The variation curves of geoelectric field value with the conductivity and frequency of the first layer and the second layer considering the induction field.The blue,red and orange lines have frequencies of 0.01 Hz,0.001 Hz and 0.000 1 Hz,respectively.The solid lines show the geoelectric field as the conductivity of the first layer changes,and the dashed lines show the geoelectric field as the conductivity of the second layer changes

我们进一步对比两种方法所计算的地电场差异，当我们考虑感应地磁场（方法二）时，地电场随第一层电导率的变化幅度远远超过了不考虑感应场（方法一）的情况；而方法二计算得到的地电场随着第二层电导率的变化幅度低于方法一. 这一结果表明，当考虑地下电导率模型对感应地磁场的影响时，浅部的低导层甚至会导致更严重的地电灾害，而较深部的高导结构对地电场的影响相对较小.

除了最简单的一维半空间模型，还可以采用一维分段电导率模型来计算地电场.比较常用的分段模型有欧洲的一维模型（Ádám et al.,2012）和美国的一维Fernberg（2012）电阻率模型，如图6.Viljanen等（2012）采用欧洲的一维电导率模型，并引入球面坐标，计算了欧洲多个国家的地电场和GICs以验证方法的有效性.Wei等（2013）使用Fernberg模型估算了历史上两次地磁暴时美国和加拿大南部的地电场，并得到结论：高电阻率结构的低纬度区域也面临着GICs风险.一维分段模型的优点是可以较好地描述区域电阻率分布，提高地电场模拟在较大范围内的精度，但是一维分段方法本质上与传统一维方法的区别不大，并不能描述真实电导率结构的横向变化.

图6 一维分段电导率模型.（a）欧洲（Ádám et al.,2012,http://real.mtak.hu/id/eprint/2957）；（b）美国（修改自Fernberg,2012）Fig.6 One-dimensional piecewise conductivity models of (a)Europe(Ádám et al.,2012,http://real.mtak.hu/id/eprint/2957);(b)The United States (modified from Fernberg,2012)

尽管上述提到的一维平面波法已经有很多应用，但是由于真正的地面电导率结构是三维横向变化的，因此采用简单的一维近似可能会在电性结构突变处产生较大的误差.董博等（2015）采用有限元法模拟出在大地电导率横向突变处感应地电场会出现邻近效应.Honkonen等（2018）认为三维模型与局部一维模型所计算的地电场在高纬度海岸分界处会产生巨大差异.所以，基于三维电导率模型的地电场模拟是GICs研究的重要方向（Püthe et al.,2014）.

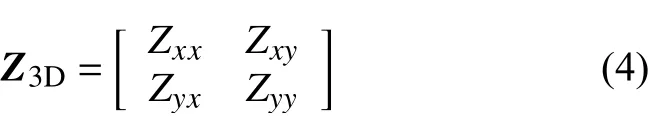
三维结构中的阻抗张量可以写为：只要已知三维阻抗张量Z3D，就可以代入公式（2）计算地电场水平分量.

获得Z3D的方法通常有两种.第一种方法是已知研究区域的三维电导率模型，通过大地电磁的正演模拟来计算阻抗张量（例如，Wang et al.,2016）.然而，详细的三维电导率模型在大部分地区是未知的.全三维模型的有效替代是三维薄板模型，即在一维层状模型上添加横向变化的电导率薄层（Vasseur and Weidelt,1977）.为了探究非一维电导率分布的影响，薄板模型已被应用于感应地电场和GICs的研究中（Beggan et al.,2013;Püthe and Kuvshinov,2013;Beggan,2015;Divett et al.,2017;Ivannikova et al.,2018）.薄板模型可以考虑地球电导率的横向变化，并模拟电导率结构突变处的地电场异常.

第二种方法是依据目标区域已有的大地电磁测量的局部电场E和磁场B，直接计算该测点处的阻抗张量（例如，Lucas et al.,2020）.局部大地电磁测量是获得良好的区域阻抗张量，并将地磁场的变化映射到地电场的最佳方法（Pulkkinen et al.,2017）.目前，在全球范围内已经进行了一些密集的MT勘探工作，比如北美的USArray项目（Schultz,2010）、澳大利亚的AusLAMP项目（Duan and Kyi,2018）和中国的SinoProbe计划（Dong et al.,2013）.但许多地区并没有足够密集的MT观测数据，这也限制了三维阻抗在计算地电场中的应用.

上述介绍的平面波方法大多使用了频率域的公式，但时域公式也已得到开发和应用（Viljanen and Pirjola,1989;Marti et al.,2014;Kelbert et al.,2017）.时域方法的开发有助于实现GICs的实时估计，为GICs预警提供理论基础.

尽管目前大部分GICs研究都是基于平面波假设，但是该方法忽略了电离层电流的分布及其强度差异，可能会导致在大磁暴期间对地电场估算的不准确（Kelbert et al.,2017）.此外，不同纬度的空间电流体系模式不同，目前普遍认为在中低纬区域产生地磁扰动的重要因素是环电流，而在高纬度地区产生地磁扰动的主要因素是磁层亚暴导致的极光电集流（Zheng et al.,2013;Ngwira and Pulkkinen,2018）.平面波假设可以很好地描述低纬度区域的电流源，但并不适合高纬度地区.

3.2 地电场的其他计算方法

Püthe和Kuvshinov（2013）提出将全球电流源表示为在地球上方流动的横向变化的球面薄层等效电流，采用球谐系数展开法进行求解.由于频率域内的磁场和地电场可以表示为关于源的线性组合，因此可以将电流源表示为球谐系数的组合，并利用麦克斯韦方程计算出频率域内每个球谐系数对应的“单位”磁场和“单位”电场的分布，之后再进行线性叠加，从而计算出全球的地电场分布.他们在沿海地区的地磁台站验证了该方法，并讨论了一维和三维薄板电导率模型所计算的地电场的区别.但是上述方法具有一定的局限性，他们假设的电流源只有大尺度结构，因此仅使用次数和阶次最多为3的球谐函数来描述源，仅适合于中低纬度区域的电磁模拟，并不足以描述高纬度区域的电离层电流源.

Honkonen等（2018）没有采用地面地磁场观测数据，而是结合了MHD方法（SWMF模型），利用太阳风参数模拟地球表面的外源磁场的时空分布，再采用上述Püthe和Kuvshinov（2013）提出的球谐系数展开法模拟出薄层等效电流源，并计算全球地电场的时空分布.他们得到结论：考虑地球三维电导率结构会导致横向电导率骤变区域的地电场显著增强（比如沿海区域），尤其是对于纬度较高的地区.

Marshalko等（2021）针对高纬度地区，对比了基于平面波法、SECS法和SWMF模型的三维电磁场的模拟结果.图7展示了在ABK台站处采用三种方法所计算的三维地磁场和地电场的模拟值以及观测值.他们认为相比于SWMF模型，使用SECS方法构建的源可以更准确地再现研究区域的磁场扰动.使用SECS方法与平面波法所计算的地电场之间存在差异，特别是在电导率横向对比强烈的地区（例如海岸）和更高纬度的区域.

图7 采用三种方法计算的三维电磁场的模拟值以及观测值.（a）～（c）Abisko（ABK）地磁观测站于2017年9月7日20:00 UT至2017年9月8日03:59 UT地磁场的模拟结果和观测值.（d）～（e）地电场的模拟结果.黑线表示地磁场的观测值；绿线表示基于平面波法的三维地电场模拟值；紫线表示基于SECS法的三维电磁场模拟值；红线表示基于SWMF模型的三维电磁场模拟值（修改自Marshalko et al.,2021）Fig.7 The time series of the modeled and observed 3-D electromagnetic field calculated by three methods.(a)~(c)The modeled and observed time series of geomagnetic field at Abisko(ABK)geomagnetic observatory from 20:00 UT,September 7,2017 to 03:59 UT,September 8,2017.(d)~(e)The modeled time series of geoelectric field.The black lines represent the observed value of the geomagnetic field,the green lines represent the modeled time series of the 3-D geomagnetic field based on the plane-wave method,the purple lines represent the modeled time series of the 3-D electromagnetic field based on the SECS method,and the red lines represent the modeled time series of the 3-D electromagnetic field based on the SWMF model(modified from Marshalko et al.,2021)

4 导体系统中GICs的计算

在完成了地面地磁场重建并计算了感应地电场后，就可以利用地电场来计算导体系统中的GICs值.地面导体系统可以分为离散接地（例如电网）和连续接地（例如油气管道）两种类型.前者在变压器处有离散的接地点，后者则通过导电性很小的绝缘材料连续接地.铁路系统则是两者兼具：铁轨中的电力设备是离散接地，而铁轨是连续接地（Pirjola,2002）.

两种接地类型需要采用不同的方法来计算GICs：离散接地是利用矩阵的形式来计算（Lehtinen and Pirjola,1985），而连续接地则是采用分布式源传输线理论（Distributed Source Transmission Line,DSTL）计算（Boteler, 1997）.

4.1 离散接地系统中的GICs计算

对于离散接地系统，比如电网，地磁暴期间产生的GICs在电网中流通的等效模型如图8所示.

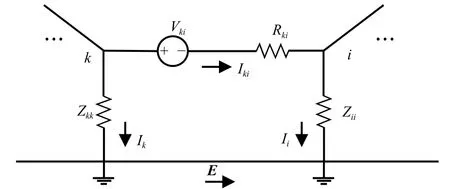
图8 GICs在电网中流通的等效模型（修改自刘同同等，2011）Fig.8 Equivalent model of GICs in power grids(modified from Liu et al.,2011)

Lehtinen和Pirjola（1985）提出流入变压器中性点的电流可以写为矩阵的形式：

式中，1是单位矩阵，Y和Z分别是网络导纳矩阵和接地阻抗矩阵，J是各节点的入地GICs电流组成的列矩阵.导纳矩阵Y利用网络中的导体电阻率来计算：

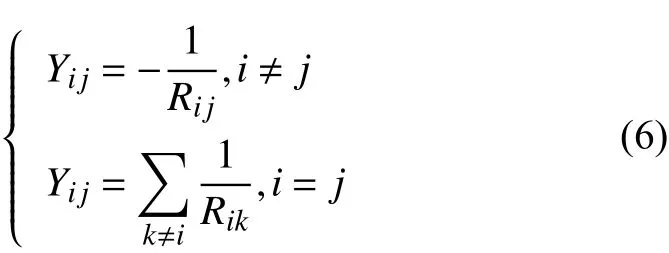
式中，Rij和Rik表示两节点之间的等效电阻.

Vki是节点k和i之间输电线路上的等效电压源，可以表示成随时间变化的沿输电线路的地电场积分：

若定义Ji为从电网流入节点i的所有电流Iki之和.根据欧姆定律，Ji可以写为：

将公式（6）和（8）代入（5）中，即可以计算变压器中性点的GICs.已有很多基于上述公式的GICs模拟（例如，Beggan,2015;Marshall,et al.,2017;Viljanen and Pirjola,2017）.

从以上公式中可以看出，GICs是地电场沿输电线路积分的时间函数.GICs的计算并不依赖于单点的电场，而是取决于输电线路上电场的积分.正是因为这种积分效应，尽管感应地电场的空间差异很大（Bedrosian and Love,2015），真实的三维地电场所产生的线电压仍可以用一维平均电场的等效电压来近似（Viljanen et al.,2006,2012）.因此，一维近似电阻率结构对于大部分GICs研究而言是足够准确的.然而，这也并不意味着一维与三维方法是完全等价的，一维的方法有其固有的局限性，在横向电导率骤变的区域，比如海岸，由于海陆电阻率差异而导致的海岸效应无法通过输电线积分来描述（Honkonen et al.,2018; Ivannikova et al.,2018;Liu et al.,2018）.因此，采用三维电阻率的方法可以有效地改进特定地质环境下GICs的模拟效果.

在实际的工程学计算中，通常会采用近似方法来计算电网中的GICs.在平面波假设下，如果假定地下电阻率结构是横向均匀的，那么GICs的计算可以简化为关于电场水平分量的线性叠加（Viljanen and Pirjola,1994）：

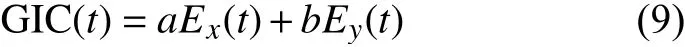
式中，a和b系数取决于电力系统的电阻和几何形状.

系数a和b通常可以根据电网模型来估算（Wik et al.,2008;Viljanen et al.,2012），如果电网模型参数未知，但是有变压器的GICs观测值，则可以采用最小二乘法来拟合a和b系数（如

Pulkkinen et al.,2007;Liu et al.,2009;Zhang et al.,2015,2020）.但是需要注意的是，最小二乘法拟合有一定的局限性，由于变压器的a和b系数由其各自的几何参数和网络配置决定，因此仅仅适用于有GICs测量值的变压器，不能将拟合得到的系数应用到周围的其他变压器上（Kelbert,2020）.

4.2 连续接地系统中的GICs计算

对于连续接地系统，比如油气管道，由于管道与大地之间隔着绝缘涂层，管道内的GICs可用分布源传输线理论来计算（Boteler,1997）.如图9所示，该理论将长距离的管道分割成许多小段，假设每小段管道的感应电场是均匀的.可用阻抗Z和并联导纳Y组成的传输线电路来等效每段管道内的电路（刘连光等，2015）.

图9 管道GICs的分布源传输线模型（刘连光等，2015）Fig.9 Distribution source transmission line model of pipelines GICs(Liu et al.,2015)

基于麦克斯韦方程可以建立管道内的传输线方程，用于描述每一段管道中由均匀感应电场E产生的电压U和电流I的分布：

电压U的解析式为：

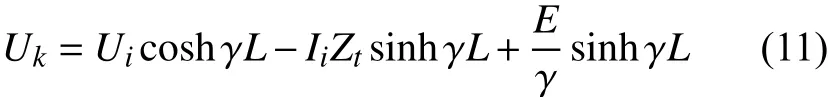
目前已有很多基于分布源传输线理论的油气管道GICs研究.Viljanen等（2006）在芬兰创建了天然气管道的监测和实时预报系统.Yu等（2019）首次实现了地磁场对管道的电磁干扰效应的监测，包括GICs和管地电位（pip-soil potential,PSP）,并且认为在中低纬度地区，中小型磁暴就会对管道造成腐蚀.Ma和Liu（2019）建立了含漏点的管网模型，讨论了不同漏点半径和位置对GICs和PSP分布的影响.Liu等（2019）就我国油气管道受GICs和管地电位的影响进行了观测实验，证实了潮汐作用对磁暴中的GICs和PSP效应的影响.

5 总结：GICs研究现状与未来

本文着重介绍了关于GICs计算方法的开发和应用，除此之外，极值灾害分析也是GICs研究的重要内容.极值灾害分析是基于统计模型，利用长期地磁观测数据来预测地磁场或地电场极值（比如百年极值），从而评估该区域的地电灾害的研究方向.全球很多区域已开展了相关工作，比如加拿大（Boteler,2001;Nikitina,2016）、日本（Watari,2015)、英国（Beggan et al.,2013)、澳大利亚（Marshall et al.,2020）、西班牙（Torta et al.,2014）、南非（Lotz and Danskin,2017）以及美国（Love et al.,2016,2018a,2018b,2019;Lucas et al.,2020）等.

对历史事件的GICs分析只能评估区域的地电灾害风险，GICs研究的最终目的是监测、预报并规避极端天气对基础设施造成的灾害，因此对GICs的实时估计以及预报是研究的关键目标.GICs的实时估计需要基于时间域的感应地电场模拟方法（Viljanen and Pirjola,1989;Marti et al.,2014;Kelbert et al.,2017），并且对计算效率有较高要求.GICs预报实际上是地磁场预报和GICs实时算法的结合，其中地磁场预报涉及到空间天气的观测和相关研究. 在拉格朗日L1点附近的先进成分探测器（advanced composition explorer,ACE）和深太空气候天文台（deep space climate observatory,DSCOVR）观测到的太阳风数据比地面遭受磁暴的时间提前20 min至1小时（Kelbert,2020），可以用于MHD模型的输入，并进行GICs的短期预报（Pulkkinen et al.,2013;Glocer et al.,2016）.此外，机器学习方法也是很有前景的GICs预报方法（如Bobra and Ilonidis,2016;Camporeale et al.,2018;Gruet et al.,2018;Camporeale,2019）.

尽管目前GICs的研究已经取得了很大进展，但仍然存在着许多重大的挑战.目前，我们对太阳风—磁层—电离层耦合关系的了解还不够透彻.明确诱发极端GICs的空间天气因素并确定磁层—电离层对其的响应，有助于更好地模拟空间电流源，从而更准确地计算感应地电场和GICs.并且，我们对地电场和GICs的预测能力仍然非常有限.虽然MHD方法具备预测的能力，但是其模拟效果不够精确，仍需进一步改进.同时，高质量的地球空间测量对于GICs研究至关重要.获取更多的地球空间观测也将有助于提高我们建模能力的准确性.另外，量化GICs的危害需要多学科的交叉和合作，从地球物理学到电气工程学，如何更好地融合不同学科的知识，也是GICs研究领域的重要任务.

致谢

感谢两位审稿人和责任编辑对本文提出的建设性意见.感谢北京大学课程“地球物理研究的论文写作指导”（课程号01201110）为本综述的完成提供了支持.

附中文参考文献

董博，王泽忠，刘连光，等.2015.大地电导率横向突变处磁暴感应地电场的邻近效应[J].地球物理学报，58（1）：238-246.

李金铭.2005.地电场与电法勘探[M].北京：地质出版社.

刘春明.2009.中低纬电网地磁感应电流及其评估方法研究[D].北京:华北电力大学.

刘连光，刘春明，张冰，等.2008.中国广东电网的几次强磁暴影响事件[J].地球物理学报，2008（4）：976-981.

刘连光，张鹏飞，王开让，等.2015.基于大地电导率分层模型的油气管网地磁暴干扰评估方法[J].电网技术，39（6）：1556-1561.

刘同同，刘连光，邹明.2011.基于分层大地电导率模型的电网GIC算法研究[J].电网与清洁能源，27（5）：26-30.