基于小波包能量熵和GWO-SVM的滚动轴承故障诊断

2022-11-07谢小正赵荣珍吕伟前

兰州理工大学学报 2022年5期

谢小正, 王晋, 赵荣珍, 李俊, 吕伟前

(兰州理工大学机电工程学院, 甘肃兰州 730050)

滚动轴承是旋转机械设备必不可缺的关键零件，其运行状态直接影响整个系统的运行安全[1].

滚动轴承在实际运行中受各种因素影响较大，因此，采集的振动信号往往具有非线性、非平稳的特点.大部分学者采用经验模态分解(EMD)、集合经验模态分解(EEMD)、变分模态分解(VMD)、小波分析对滚动轴承振动信号进行分解[2].EMD存在模态混叠、端点效应，影响着信号分解效果.对此，Wu等[3]提出了EEMD，在振动信号中加入白噪声来抑制模态混叠，但是效果依旧不理想.2014年，Dragomiretskiy等[4]提出了VMD，在一定程度上较EMD和EEMD有所提高，但是VMD在最优分解层数和惩罚因子这2个参数选取方面存在困难.小波分析只对低频部分进行分解，没有对高频部分进行分解,容易导致故障特征的遗漏.小波包可以实现低频、高频部分的精细划分，具有多分辨率的特点，非常适合轴承非平稳、非线性振动信号的分解，并且小波包理论在滚动轴承故障诊断中已经被广泛地应用[5-7].

在信号分解后，对信号特征进行描述也是关键问题.熵可以很好地对信号的不确定性和复杂度进行表述.小波包能量熵是小波包理论与信息熵理论相结合的产物，可以体现滚动轴承故障信号的深层故障特征，并且可以对滚动轴承故障信号的复杂度进行量化表示[2].

滚动轴承故障诊断的实质是提取特征向量后的分类问题.在滚动轴承实际运行中，能够获得的故障样本数量较少，而支持向量机(SVM)对小样本数据有非常好的分类能力，只是SVM分类准确性受自身参数影响较大.大量学者应用优化算法对SVM参数进行优化.Wang等[8]针对高速航空发动机轴承早期微弱故障的定量诊断问题，提出了基于支持向量机的智能诊断方法，并利用粒子群优化算法(PSO)对SVM的参数进行优化.时培明等[9]提出了基于分形维数和GA-SVM的风电机组齿轮箱轴承故障诊断方法，GA-SVM模型很好地解决了参数选择的问题.相比PSO和遗传算法(GA)，灰狼优化算法(GWO)结构简单，容易理解，收敛速度快，运行时间短，非常适合SVM参数的优化.

综上所述，针对滚动轴承故障特征提取和SVM参数选择困难等问题，本文提出了基于小波包能量熵和GWO-SVM的滚动轴承故障诊断方法.该方法将提取的小波包能量熵作为滚动轴承故障的特征向量，用GWO算法优化SVM惩罚因子c和核函数g，以训练集错误率最小为优化目标，对训练集进行训练，满足终止条件，输出优化好的SVM模型.并将测试集输入到由GWO优化好的SVM模型中，验证对滚动轴承不同故障类别和不同损伤程度的识别准确率.结果表明，相比其他方法，本文所提方法有更高的识别准确率.

1 理论方法

1.1 小波包能量熵特征提取

滚动轴承的振动信号是长度为N的离散时间序列{y(i)}，则小波包能量熵的特征向量提取过程如下：

1)对滚动轴承振动信号时间序列{y(i)}进行j层小波包分解，得到2j个节点，Cm，k(m=1，2，…，j;k=0，1，2，…，2j-1)代表第m层的第k个节点，每个节点的小波包系数代表1个频带的信号特征.

2)分别提取每个频带从低频到高频的小波包系数Dm，k.

3)第m层各个频带的能量值Em，k为

(1)

式中：Dm，k(t)为小波包重构系数；t为相应频带信号的时间.

4)根据熵的定义，第m层各个频带的能量熵Hm，k为

(2)

其中，

(3)

式中：pm，k为第m层第k个频带在第m层总能量中所占的比重；E为总能量.

1.2 灰狼优化算法

2014年，Mirjalili[10]等提出了新的群体智能优化算法——灰狼优化算法.GWO的狼群组织为典型金字塔结构，最顶层为α狼，第2层为β狼，第2层为δ狼，最底层ω狼是所有狼群的基础.狼群捕猎分为3个阶段，即追踪阶段、包围猎物、攻击猎物.

建立GWO数学模型.假设t为迭代次数，Xp为猎物位置向量，X为狼群位置向量，则狼群与猎物之间的距离D为

D=|C·Xp(t)-X(t)|

(4)

狼群不断改变位置，则：

X(t+1)=Xp(t)-A·D

(5)

式中：A、C分别为系数向量，即

(6)

式中：r1、r2∈[0,1]的随机向量，a为收敛因子，即

(7)

式中：Mmax为最大迭代次数.

狼群围捕猎物位置变换为

式中：Dα、Dβ、Dδ为对应α、β、δ狼与猎物的距离；A1、A2、A3和C1、C2、C3为对应于α、β、δ的系数向量;Xα(t)、Xβ(t)、Xδ(t)为t时刻猎物具体位置;X1、X2、X3为对应狼群的位置向量;Xα、Xβ、Xδ为对应猎物的位置向量.

1.3 支持向量机原理

训练集B={(x1，y1)，(x2，y2)，…,(xi，yi)，…,(xn,yn)}，xi∈R，R为所有样本集合，yi∈{1，-1}为xi所属类别.超平面方程为wx+b，其中，w为权值向量，b为阈值.则区分样本,并使分类间隔距离最大的优化问题能在约束条件yi(wTw+b)≥1-ζi下最小化为

(10)

式中：c为惩罚因子；ζi为松驰变量，ζi≥0.

引入拉格朗日乘子和KKT条件，通过在最优超平面中引用适当的内积函数K(xi，xj)，将线性不可分问题转化为某个高维空间的线性可分问题.则最大化问题就转变为

(11)

分类函数为

(12)

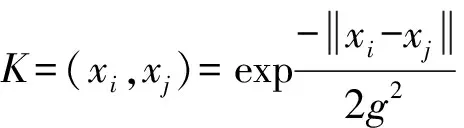
SVM主要是处理二分类问题的，而滚动轴承故障是多分类问题，因此可以采用一对一的方法来构造多分类模型[11].

2 本文所提故障诊断流程

应用上述理论，本文提出了小波包能量熵和GWO-SVM的滚动轴承故障诊断方法.该方法充分考虑了小波包可以对信号进行更精细的划分，拥有多分辨率分析的优势;能量熵可以体现滚动轴承故障信号的深层故障特征，以及支持向量机具有分类准确率高的特点.但是SVM分类准确率受惩罚因子c和核函数g的影响较大,用GWO的核心就是采用GWO优化SVM的惩罚因子c和核参数g，通过选择最佳的参数组合[c，g]，以此来提高分类的准确率.本文所提滚动轴承故障诊断方法实现过程如图1所示.

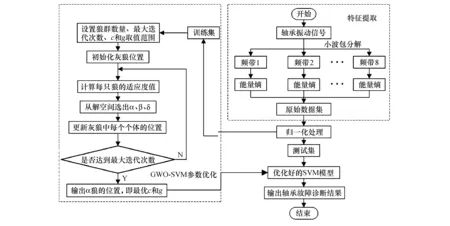
图1 小波包、GWO-SVM故障诊断流程

2.1 特征提取

1)将不同故障类型、不同损伤直径和正常状态滚动轴承振动信号(共10种类别)进行3层小波包分解.

2)对第3层小波包分解系数进行重构，计算其能量值并进行归一化处理，计算各频段的能量熵并作为特征向量，对特征向量进行归一化处理，并将归一化后的特征向量分为训练集和测试集.

2.2 GWO优化SVM

1)设置狼群数量、最大迭代次数、优化参数c和g的取值范围.

2)随机产生灰狼种群，每个灰狼群个体位置向量由c和g组成.

3)依据初始的参数c和g，通过SVM对训练集样本进行训练，个体的适应度值用训练集的识别准确率表示.

4)计算每只灰狼的适应度值，根据适应度值将灰狼分为α、β、δ、w共4个等级，对灰狼种群中每个个体进行位置更新.

5)若迭代次数超出最大迭代次数，寻优结束，输出最优的参数c和g；否则跳转至4)继续参数寻优，从而获得最优SVM分类模型.

2.3 测试集分类

将测试集输入到由GWO优化好的SVM模型中，从而输出滚动轴承故障诊断结果.

3 实验结果与分析

3.1 实验数据

为了验证本文所提故障诊断方法的准确性，选用美国凯斯西储大学轴承故障数据.选取靠近驱动端轴承的振动信号，电机负载为0 hp，转速为1 797 r/min，采样频率为12 kHz.故障类型包括滚动轴承的内圈、外圈、滚动体单点故障，其内圈、外圈、滚动体故障的损伤直径分别包括0.177 8、0.355 6、0.533 4 mm(故障深度都为0.28 mm).根据不同的故障位置和不同的损伤直径可划分为9种不同类别故障，再加上正常状态滚动轴承振动信号，共10种类别.每种类别取50个样本，每个样本包含2 048个采样点，以3∶2的比列随机划分训练集和测试集，即每种类别30个样本作为训练集，20个样本作为测试集.数据集划分如表1所列.

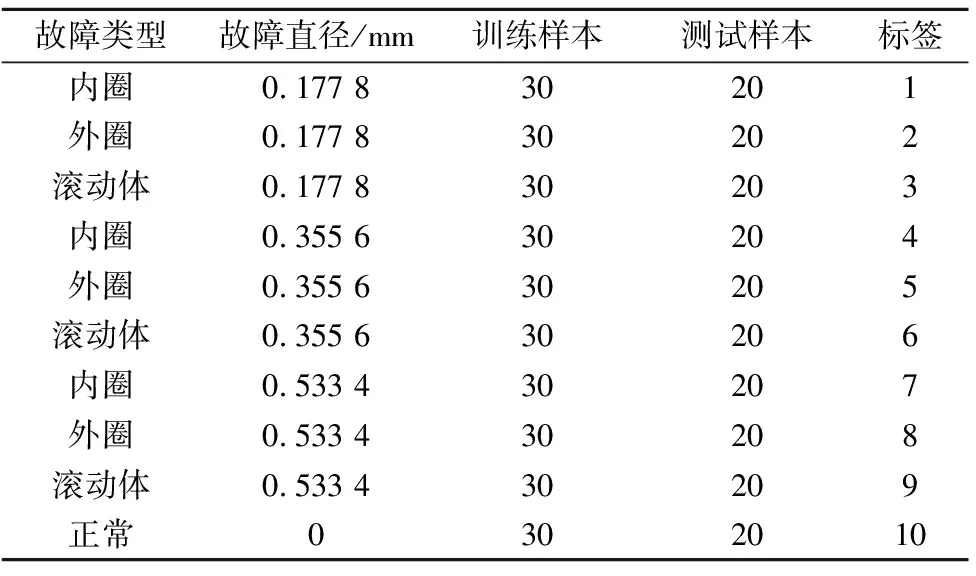
表1 故障类别分类标签

3.2 提取小波包能量熵特征

使用db5小波包分解函数对10种不同类别样本的振动信号(共500个样本)进行3层小波包分解，对第3层各频段小波包分解系数进行重构，计算各频带的能量并归一化，然后将其能量熵作为滚动轴承10种不同类别样本的特征向量.表2只列出每种类别中1个特征向量.可以看出，滚动轴承不同状态的小波包能量熵存在明显的差异，可以用于表征滚动轴承故障特征信息.

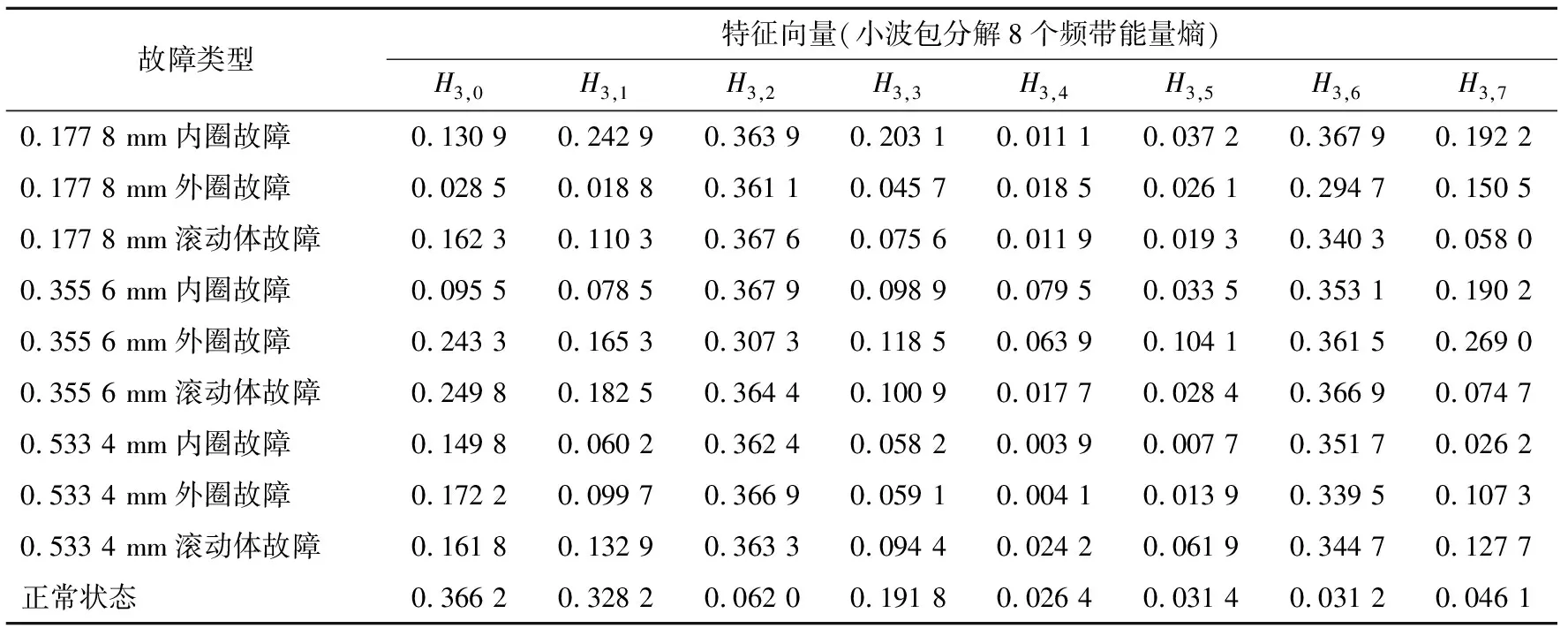
表2 故障特征向量

3.3 基于GWO-SVM的故障识别

在进行提取小波包能量熵特征向量之后，本文采用GWO对SVM参数进行寻优，GWO初始化参数及SVM参数c和g取值范围如表3所列.

表3 GWO和SVM参数设置

SVM参数寻优适应度曲线如图2所示.可以看出：经过16次迭代后，平均适应度保持在98%以上;经过4次迭代后，最佳适应度保持在99%.相比人工随机选取参数，利用GWO寻优可以提升效率，并且提高准确率.经过寻优后，c取值为19.289 6，g取值为30.256 8.使用优化后的SVM模型，进行15次运算得到平均识别率为100%，分类结果如图3所示.

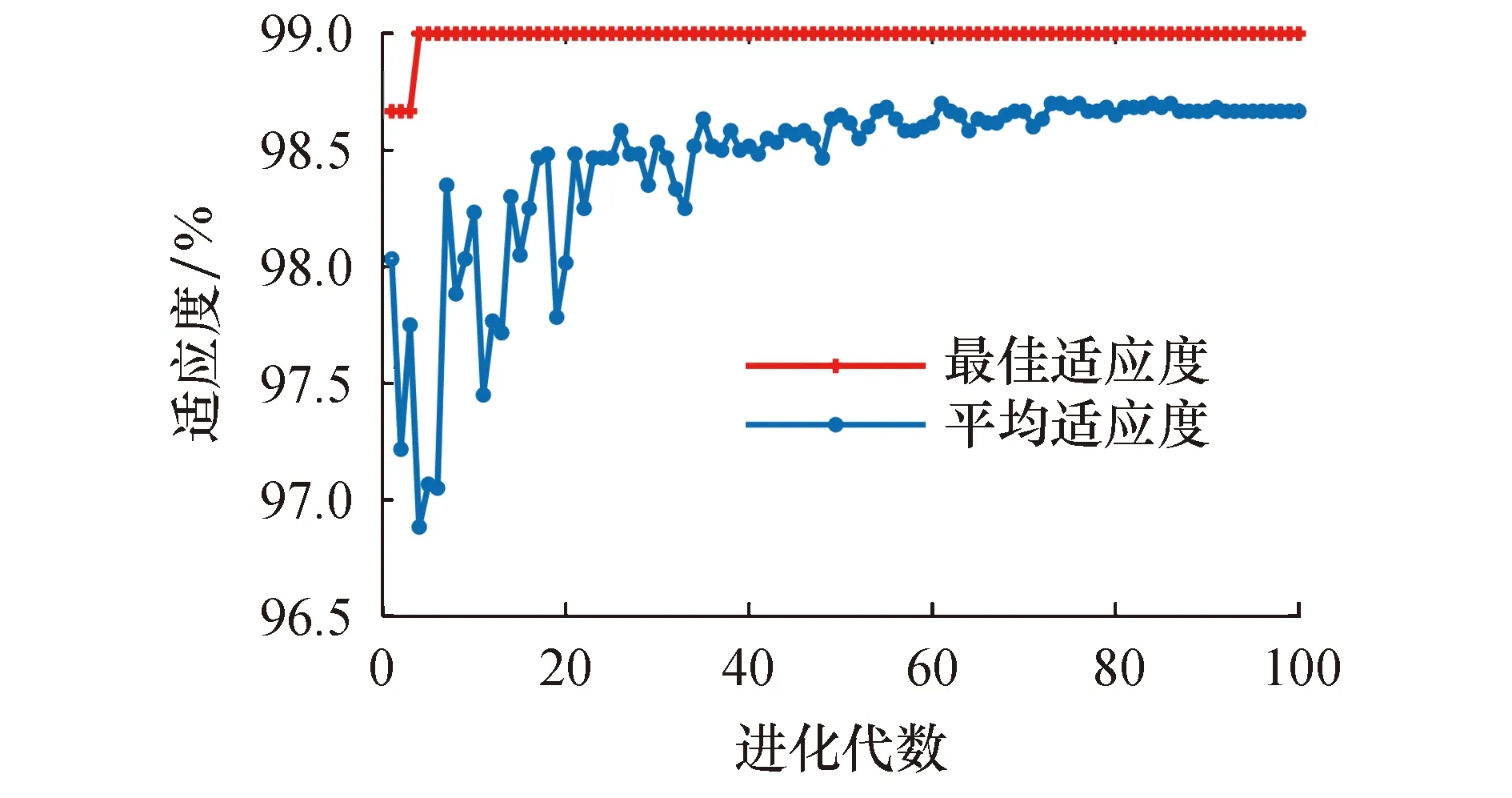
图2 GWO-SVM参数寻优适应度曲线

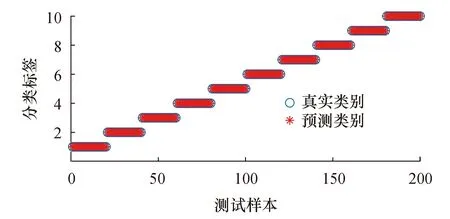
图3 小波包能量熵和GWO-SVM测试集分类效果

3.4 对比实验

为验证本文所提方法在轴承故障诊断方面的有效性和准确性，设计了以下对比实验，即基于小波包能量熵和GWO-SVM、基于EEMD能量熵和GWO-SVM、小波包能量熵和未优化SVM.

在基于EEMD能量熵和GWO-SVM的实验中，选取损伤直径为0.177 8 mm的内圈、外圈、滚动体故障和正常状态的振动信号分别进行EEMD分解，同时计算9阶IMF能量并进行归一化处理，如图4所示，前5阶的能量占比达到95%以上.因此，取前5阶的IMF分量计算能量熵构造特征向量，部分EEMD能量熵特征向量如表4所列.将测试集输入到由GWO优化好的SVM模型，识别准确率为95%，分类结果如图5所示.

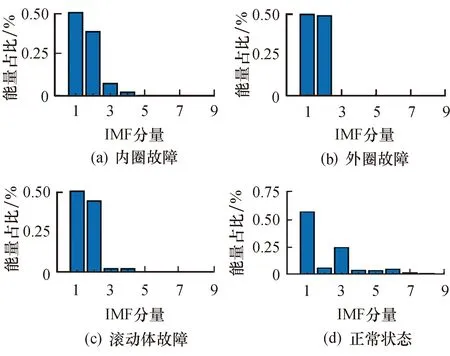
图4 IMF分量能量占比

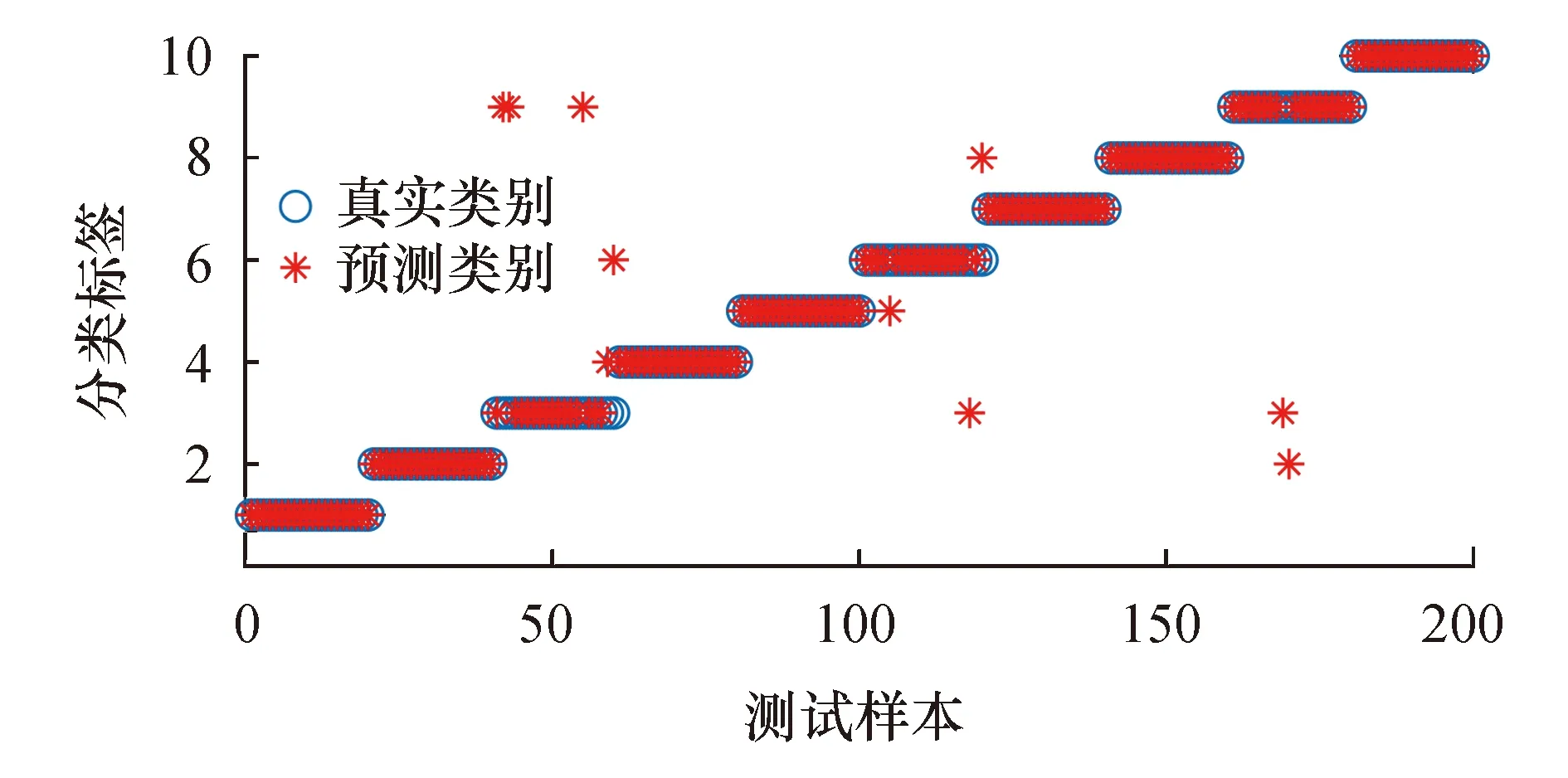
图5 EEMD能量熵和GWO-SVM测试集分类效果

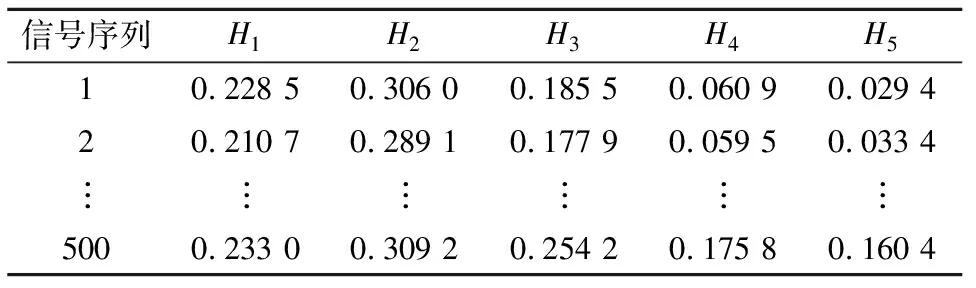
表4 部分EEMD能量熵特征向量

在小波包能量熵和未优化SVM实验中，人工选取惩罚因子c=30.012 1，核函数g=20.213 6，特征向量选用小波包能量熵.将测试集输入到未优化SVM模型，识别准确率为94%，分类结果如图6所示.

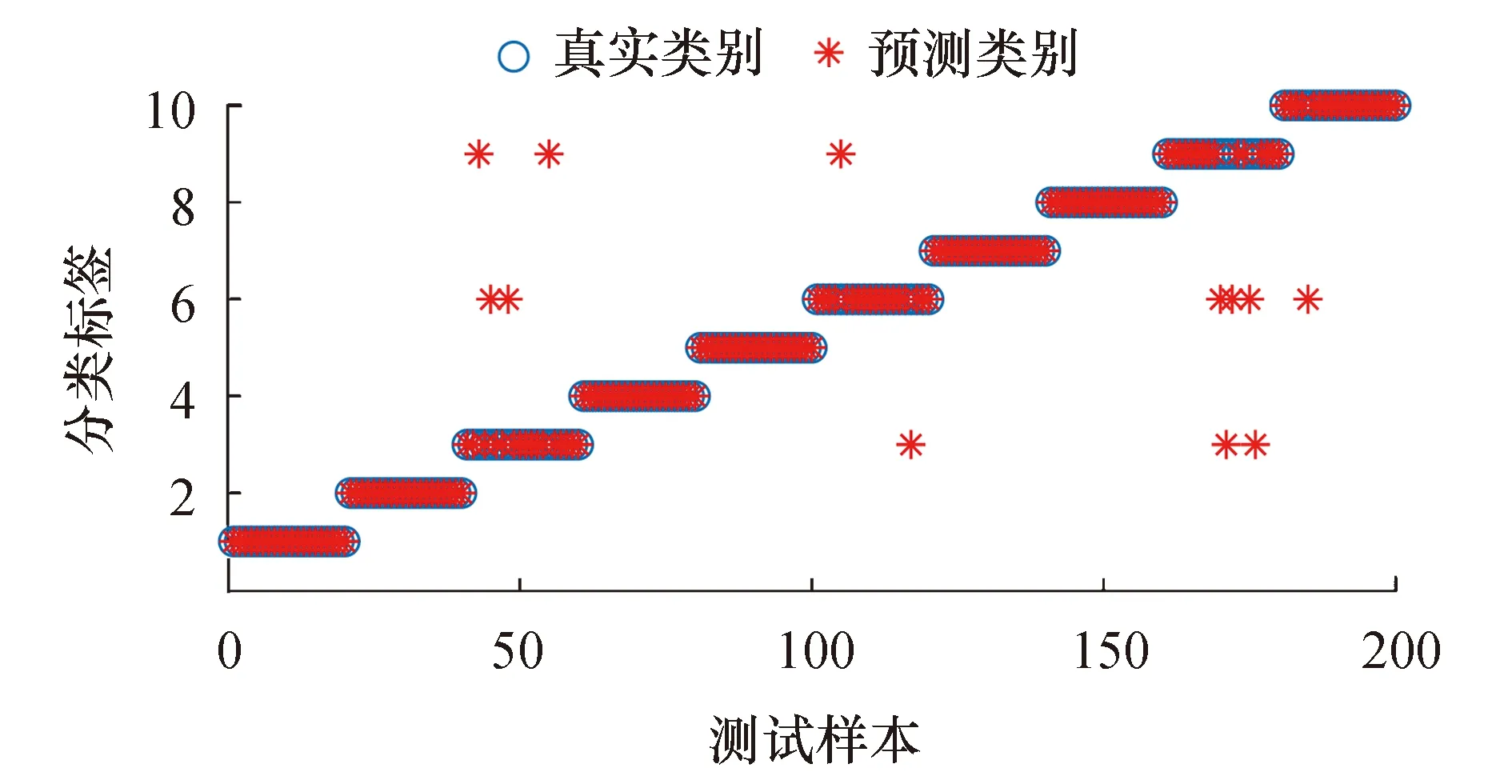
图6 小波包能量熵和未优化SVM测试集分类结果

通过小波包能量熵和GWO-SVM、EEMD能量熵和GWO-SVM对比实验可以发现，相比EEMD小波包可以对滚动轴承振动信号高频和低频部分进行精细分解，准确提取故障特征.同时，EEMD能量熵和GWO-SVM、小波包能量熵和未优化SVM对比实验表明，相比根据人工经验选择SVM参数，利用GWO可以较准确地选择SVM参数，进而SVM的分类准确率较高.

为了进一步验证小波包能量熵和GWO-SVM在滚动轴承故障诊断方面的有效性和准确性，将该方法与其他特征提取方法和不同分类器的识别准确率进行对比，对比结果如表5所列.

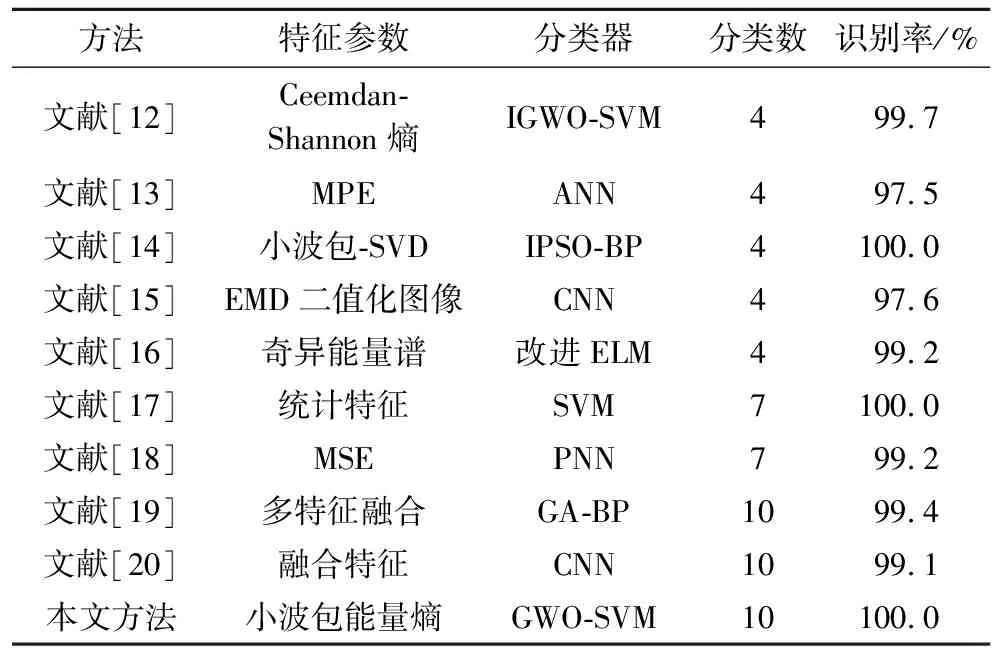
表5 不同特征和分类器识别对比

文献[12-16]中的方法针对轴承内圈、外圈、滚动体和正常状态滚动轴承识别都有较好的识别准确率，但是只区分了故障类型，没有区分故障损伤程度.文献[17-20]中的方法针对故障类型和故障损伤程度都进行了识别.通过对比发现，不同的特征向量和分类器对识别准确率有一定影响.其中，支持向量机的分类准确率较其他分类器较高；卷积神经网络(CNN)需要大量的样本进行训练，存在一定的限制；融合特征较单一特征可以更加充分地表示滚动轴承故障特征.因此，本文方法在考虑不同故障类型和不同损伤程度并保证算法简单的前提下，相比文献中其他方法有更高的识别准确率.