磁流体加速性能影响规律的数值研究

叶启航, 鹿 鹏, 刘欣怡, 黄护林, 化为卓, 李益文

(1. 南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室, 江苏 南京 210016; 2. 空军工程大学 等离子体动力学重点实验室, 陕西 西安 710038)

随着科学技术的进步,人们对于飞行器的飞行速度要求日益提高,高超声速飞行器的研究得到了研究人员的广泛关注[1-3]．作为能够突破现有高超声速飞行器设计理念的发展方向之一,磁流体动力学技术受到了全球研究人员的重视[4-6]．磁流体动力学(magneto-hydro-dynamics, MHD)是流体力学和电动力学的交叉学科,主要研究导电流体(如气态等离子体、液态金属、电解液等)在磁场作用下的运动规律[2]．在航空航天领域中,磁流体动力学的主要研究对象为气态等离子体,所以也称磁控气动力学[3](magneto aero/gas dynamics, MAD/MGD)或磁激等离子体动力学[4](magneto plasma dynamics, MPD)．

I.ADAMOVICH等[7]开展了未加电离种子和加电离种子条件下的 MHD 加速研究,采用化学非平衡电离的气体模型分析了MHD加速的可行性．NASA Ames研究中心利用激波管和磁流体加速通道进行了磁流体加速试验研究[8],研究表明:在0.92 T的平均磁感应强度作用下,最大加速效果可达40%;将磁感应强度提升为3.0 T可以使加速效果达到120%．H.ASANO等[9]研究了放电性能对非平衡等离子体MHD加速器加速性能的影响,结果表明均匀放电不仅有利于增加气流速度,还可以获得较高的加速效率．A.M.SUKARSAN[10]数值研究了磁流体动力加速器中施加的磁场和电流的效率,结果表明MHD加速器的电效率随施加的磁场和电输入的变化而变化．I.KUZOVATOV等[11]完成了在平面MHD加速器通道中流动的非稳态过程的数学建模,数值解决了具有Hall效应的磁流体动力学二维问题．M.ANWARI等[12]对使用非平衡空气等离子体作为工作气体的MHD加速器进行了研究,使用一维数值模拟评估了MHD加速器在不同水平的外加磁场下的基本性能(例如流动性能和电气性能)．张杨等[13]开展了不同磁感应强度下的磁流体加速试验研究,发现随着磁感应强度的增加,磁流体加速效率呈现下降的趋势,同时研究结果还表明电导率对输入功率影响较大,要提高加速效果须同时提高气流的电导率和加速通道的电效率．LI L.等[14]运用氩气等离子体用作工作气体对不同配置磁场下的加速通道进行了数值研究,获得了磁场配置对等离子体电离和流动特性的影响．关于电极及其布置,S.PROMSON等[15]研究了电流分布与电极布置的关系,并得到了对角加速通道内部的电流矢量分布图．

然而,当前对于电极布置方式的研究仍不够充分,由于导电流体在加速通道内部的流动涉及电场、磁场等多物理场的耦合,流动状况复杂,外加磁场、扩张角度、进口条件以及电极布置方式等的改变都会引起通道内部流动状况的变化．因此,只有深入了解外加条件的改变对于加速通道内部流动的影响规律,才能更好地实现对导电流体的加速．文中基于MHD模块,加入自主编写的UDF程序,利用UDS方程求解电势方程,综合计算考虑Maxwell方程组和等离子体动力学方程组的流体力学方程组,技术上利用自主开发的程序改变能量方程的源项实现,数值研究各种外加条件对于磁流体加速通道内部流动以及加速性能的影响．

1 数学模型

磁流体加速通道简化模型如图1所示.通道入口的高度均为30 mm(沿y轴方向),宽度均为30 mm(沿z轴方向),长度为300 mm(沿x轴方向)．设置的通道扩张角度均为1°．

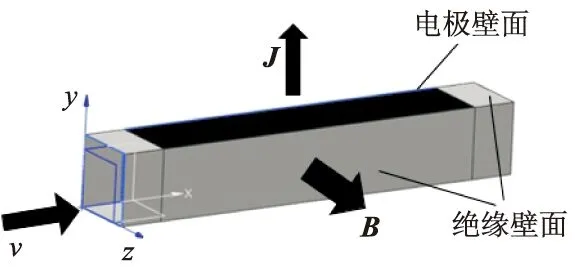
图1 磁流体加速通道示意图

1.1 控制方程

对于黏性气体流动,考虑MHD源项的三维非稳态可压缩黏性流体流动的Navier-Stokes方程如下:

(1)

式中:

其中:B是沿z轴正方向的磁场强度;e为单位体积气体的总能;E为电场强度矢量;J是电流密度矢量;P为气体压力;T是气体静温;ρ为气体密度;t为时间;u、v、w分别为x、y、z方向的速度分量,x、y、z分别指向流动方向、磁场方向、法拉第电流方向;τ为黏性应力张量：

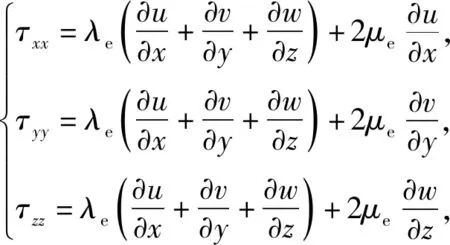
(2)

(3)

μe=μl+μt,λe=λl+λt,

(4)

(5)

式中:k为热导率;μ为动力黏度系数;λ为第二黏度系数;下标e、l、t分别表示有效值、层流值、湍流值．

磁流体加速器是在外加的电场和磁场的耦合作用下进行工作的,磁流体动力学方程组中包含了Maxwell方程组,广义欧姆定律．

Maxwell方程组:

×B=0,

(6)

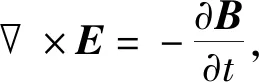
③徐飞.情理兼融，偏重阐释——2017年江苏高考作文题简析及备考启示[J].中学语文教学参考,2017(19):72-74.

(7)

·D=q,

(8)

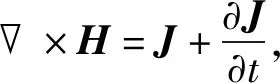
(9)

式中:B和E分别为磁场和电场;H和D分别是感生磁场和感生电场;q为电荷密度;J为电流密度矢量．

由于加速通道内的磁雷诺数很小,因此可以忽略电流引起的感生磁场,并且由于通道内部流体的速度比光速小得多,所以Maxwell方程组中的位移电流项∂D/∂t可以忽略不计;在外加磁场为恒定磁场的情况下,∂B/∂t=0;故由Maxwell方程组可得·J=0且×E=0．

广义欧姆定律:

J=σ(E+U×B)-β(J×B),

(10)

式中:σ表示电导率．根据·J=0以及式(10)推导出

-·(σφ)+σ[·(U×B)+βB·U]=0,

(11)

式(11)即为需要求解的电势方程,求出电势之后再根据广义欧姆定律即可求出电流密度,进而求出流体所受到的磁场力和加速等性能参数．

电流密度公式为

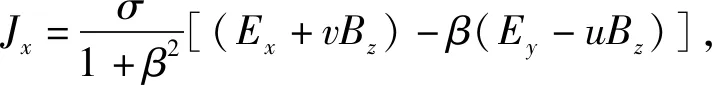
(12)

(13)

Jz=σEz．

(14)

1.2 计算模型与边界条件

通道模型为三维渐扩通道模型,采用的电极布置方式为上下壁面(与y轴垂直的两个壁面)间隔式布置等长度的电极,电极对数有8对和12对两种．采用的外加电势条件均为150 V,采用外加磁感应强度为1.5、2.0 T的初始条件进行模拟计算．通道模型如图2和图3所示,其宽度均为30 mm(沿x轴方向),高度均为30 mm(沿y轴方向),长度均为300 mm(沿z轴方向),扩张角度均为1.12°,电极的总长度均为192 mm,第一对电极距离进口的距离保持一致,均为15 mm．其中x轴正方向为流体流动的方向,y轴正方向为外加电势产生的电流方向,z轴正方向为外加磁场方向．为了避免端部效应的影响,每个通道前后预留了至少15 mm未加电极．

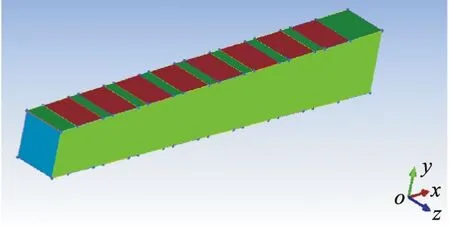
图2 电极对数为8对的通道模型

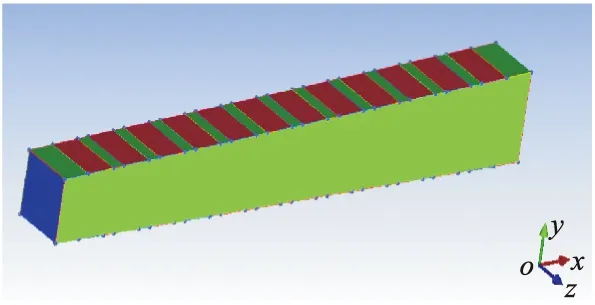
图3 电极对数为12对的通道模型

在数值计算模型方面,选择了合理的网格数量对通道进行划分,计算中使用的湍流模型是S-A模型,在MHD模块运用电势法进行计算,电势方程采用UDS输送方程进行求解,使用自主编辑的UDF添加能量方程源项,从而实现外加电能的输入及利用．通道入口处采用压力入口边界条件,通道出口处采用压力出口边界条件,壁面采用的是无滑移速度边界条件,所有壁面温度均设置为定温300 K以模拟理想化的水冷效果．其余设置的初始条件:进口静压为500 Pa;进口静温为1 000 K;进口速度为950 m·s-1;电导率为15 S·m-1．

2 数值模拟结果与分析

2.1 模型验证

为了验证计算模型的精确性,模型验证选取的是与试验数据符合较好的李益文等[16]的二维通道模型．通道的网格划分如图4所示,数值计算中使用的工质物性以及边界条件与文献中保持一致,通道进口条件为压力远场入口,出口条件设置为压力出口,边界层设置为绝热边界．上壁面10～30 mm处为阳极,下壁面10～30 mm处为阴极,其余壁面处设置为绝缘壁．

图4 模型网格示意图

图5和图6为通道电势分布对比图,图7和图8电流密度分布对比图,可以看出电势分布及电流密度分布基本一致,因此认为模型具有较高的准确性．

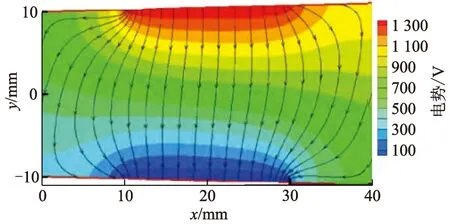
图5 文献[16]中的电势分布

图6 文中计算得到的电势分布

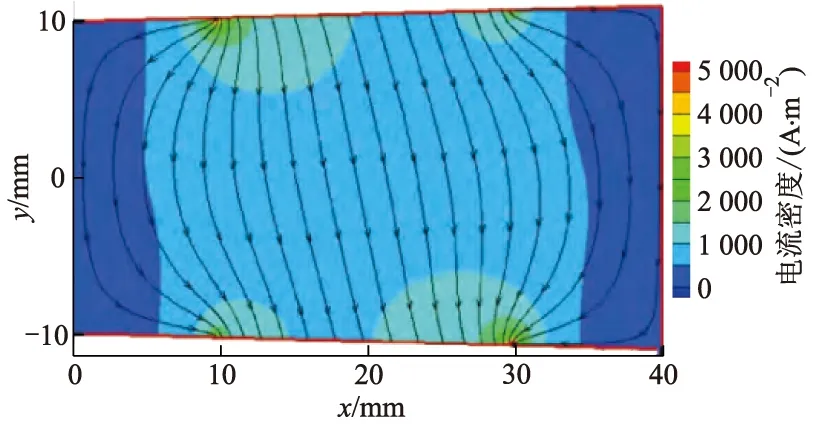
图7 文献[16]中的电流密度分布

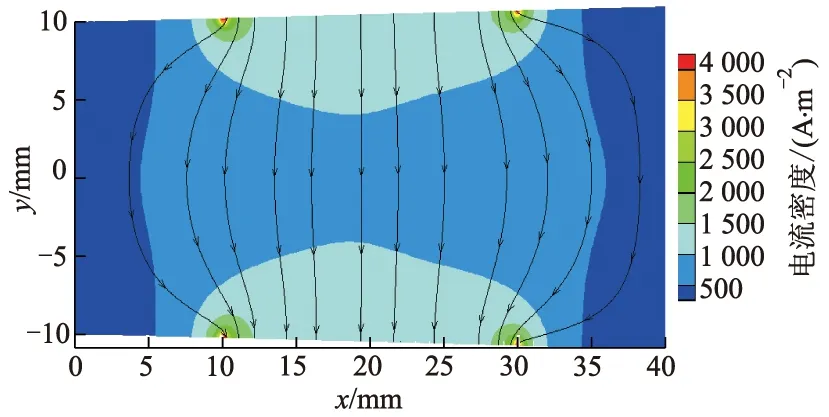
图8 文中计算得到的电流密度分布

2.2 电极布置和磁场强度对通道加速性能的影响

在采用不同外加电极对数以及磁场强度的工况下计算得到的加速通道出口数据如表1所示．

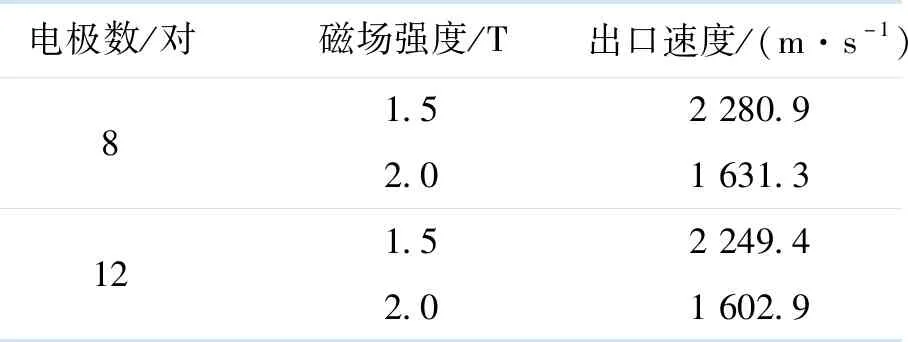
表1 计算中使用的条件

从表1中可以看出,加速通道采用了间隔式的电极布置方式后,在进口速度为950 m·s-1的条件下,外加150 V电势后能够很好地对流体进行加速．但是随着外加磁场强度增大,加速效果会减弱;在电极总长度固定的情况下,电极对数对于加速效果的影响较小．

为了更加深入地了解外加磁场对通道内部速度分布的影响,利用后处理软件截取了通道内部的z轴中心截面进行研究,在150 V,1.5 T条件下的通道内部马赫数分布如图9所示．

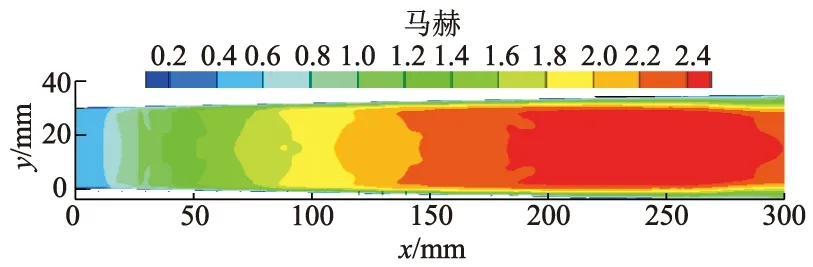
图9 150 V,1.5 T时,z=15 mm截面上的马赫数分布

对于处在各种工况下的加速通道来说,z=15 mm截面上的洛伦兹力分布情况基本一致,由于通道中间的大部分区域电流密度比较均匀,且方向沿y轴正方向,因此在外加了z轴正方向的磁场后,根据左手定则,在通道中间的大部分区域洛伦兹力都是与流体流动方向相同的,对流体起到加速的作用,如图10所示．但是需要指出的是,在通道的两端,即第一对电极和最后一对电极的外侧边缘区域,由于存在不均匀分布的电流(见图11),导致在通道两端存在方向垂直于壁面的洛伦兹力,这会对加速产生不利的影响．

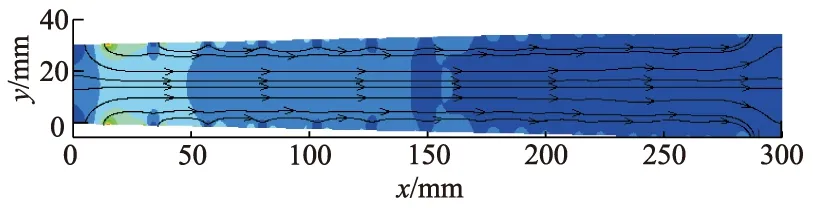
图10 150 V,1.5 T时,z=15 mm截面上的洛伦兹力矢量分布

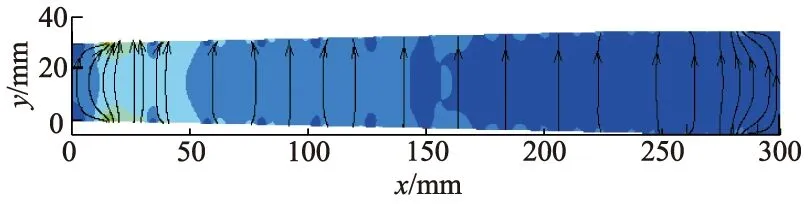
图11 150 V,1.5 T时,z=15 mm截面上的电流密度矢量分布

2.3 电极布置和磁场强度对通道内部温度的影响

不同工况下通道内部最高温度数据如表2所示．

表2 不同磁场时的最高温度

由表2可见,对于采用了间断式电极布置方式的加速通道,通道内部的最高温度随着磁场强度的提高而降低．根据广义欧姆定律可得

E·j=u·(j×B)+j2/σ,

式中:u·(j×B) 项为洛伦兹力所做的功,记为Ql;j2/σ项为焦耳热,记为Qj;E·j项是外部系统与流体之间的能量交换,记为Qe．因此,在保持外加电势恒定不变的情况下,磁场强度增大导致洛伦兹力做功项u·(j×B) 增大,因此,在外加电能E·j项基本保持不变时,磁场增大导致Ql增大,Qj减小,即通道内部的焦耳热耗散减小,因此通道内部的温度也会相应降低．

不同工况下,z=15 mm截面上速度分布如图12所示．

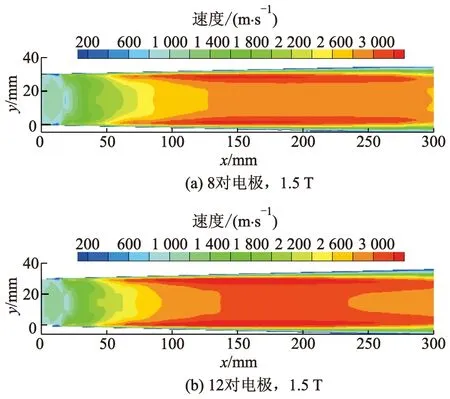
图12 电极分布对速度的影响

从图12可知,保持外加电势150 V不变,在电极的总长度一定的情况下,12对电极时的通道内部速度比8对电极时的通道内部速度稍小．而随着速度的提升,通道内部的温度会随之上升(见图13),通道内部的温度,特别是电极附近,其温度非常高,达到了3 500 K以上．这样的高温可能会影响加速通道的寿命,因此在实物加工时,需要特别注意材料的选用和散热问题．

图13 8对电极1.5 T时,z=15 mm截面上的温度分布

2.4 扩张角度对通道加速性能的影响

选用长度为400 mm的加速通道,改变扩张角度对通道加速性能的影响如图14所示．

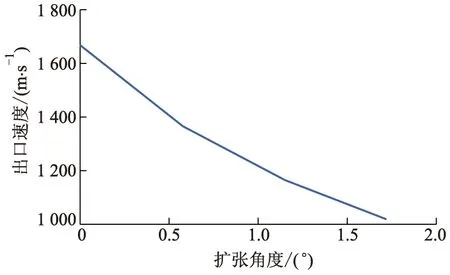
图14 不同扩张角度时的出口速度

从图14可以看出,当通道的扩张角度变大时,其出口速度呈下降趋势．为了研究其原因,查看了扩张角度分别为0°和1.72°时通道内部的速度分布云图,如图15所示．

图15 扩张角度对速度分布影响

从图15可以看出,当扩张角为0°时,该通道内的速度沿x轴方向逐渐变大,在出口段达到最大;而当扩张角为1.72°时,流体在通道前半段速度逐渐增大,而到通道后半段速度则逐渐变小．这是由于通道内部的电流密度是外加电势产生的电流以及感应电流之和,他们之间方向相反;当保持外加电势不变时增大通道扩张角度,正负电极之间的距离变大,导致通道内部的电场强度变小,电流密度也会随之减小;但是在磁场强度保持不变时,通道内部的感应电流变化并不明显,因此在施加的外加电势产生的电流密度减小时,通道内部的电流密度会减小甚至反向,这会导致加速性能的降低甚至减速．

因此,一味增加磁场强度并不能提高加速效果,还需要根据实际的工况设置合理的磁场强度．

3 结 论

1) 在外加电压为150 V条件下,由于感应电流的存在,此时继续增大磁场强度反而会导致通道后半段出现减速的现象,使得通道出口速度有所降低．

2) 随着流体速度的提升,通道内部的温度会随之提高,特别是在电极附近,其温度可达到3 500 K以上．因此在实物设计时,应当特别注意材料的选用以及电极附近的散热问题．

3) 在电极总长度不变的情况下,电极的数量对其出口速度以及最高温度影响不大．

4) 当扩张角度增加时,由于电极之间的距离变大,导致通道内部沿流场方向的电场强度逐渐减小,进而影响洛伦兹力,导致通道内部的流体速度呈现先变大而后变小的趋势．