长江口平面盐度锋对径流量变化的响应特征

2022-11-07匡翠萍武云龙

同济大学学报（自然科学版） 2022年10期

匡翠萍，陈括，武云龙，王洁

（同济大学土木工程学院，上海 200092）

长江口地形复杂多变，属中等强度的潮汐河口，外海高盐度盐水与上游冲淡水交汇于此，产生了复杂的水动力环境，盐水入侵季节性变化明显。河口上游淡水与外海盐水之间存在一个过渡带，常被称为冲淡水羽流（或羽状锋），长江羽流的范围很大，可延伸近百公里，在其核心部位往往出现一道锋面，常称其为盐度锋。实测数据显示，长江口水下沙洲的迁移与盐度锋位置的变化保持一致，这说明盐度锋对于泥沙的输运及水下三角洲的发展有一定的影响［1-2］。盐度锋附近聚集大量的微生物及污染物，易使赤潮爆发，严重影响水环境［3-4］。实测数据表明，高叶绿素a浓度的空间分布与盐度锋的位置有很强的相关性［5］。盐度锋附近污染物、悬沙、赤潮的增加加剧了氧气的消耗并阻碍了氧气的交换，被认为是长江口缺氧区形成的重要原因［6-7］。

盐度锋作为产生于河口水域的重要物理现象，对河口区潮流变化、物质输运及沉降过程有着重要影响。作为海水的辅聚区，盐度锋的典型特征就是盐度梯度大，并伴有明显跃迁现象，因而受到国内外河口研究者的广泛关注。Molinas等［8］以亚马逊河口为例，利用Delft3D模型对底层盐度锋的时空变化进行研究，得到风、径流量等因素对底层变化的不同响应程度。毛汉礼等［2］通过对长江口实测数据的分析，将长江冲淡水以主体边界和整体边界划分为两部分，以26 psu（psu指1 000 g水内溶解的无机盐克数）等盐线作为冲淡水主体边界，以32 psu等盐线作为冲淡水整体边界亦即最外侧边界。胡方西等［9］依据盐度将长江口盐度锋划分为3级，即内侧锋（河口锋）、羽状锋、外侧锋（海洋锋），分别以7 psu、25 psu及31 psu作为各级锋面的特征盐度参数，结果表明羽状锋对于物质输运乃至水下三角洲的发育至关重要。陈伟等［10］通过盐度实测资料发现，夏季象山港出现双锋面结构，冬季双锋面结构消失，并借助潮锋理论对盐度锋系统的形成机制进行了分析，进一步探究象山港盐度锋对径流量变化的响应特征。高钦钦等［11］通过ECOM（estuarine coastal and ocean model）理想河口模型，探究了盐度锋对河口环流的影响，结果表明在锋面附近出现表层向海、底层向陆的密度流，并随锋面强度降低而环流流速减弱。

近年来，随着经济的快速发展和人口的迅猛增长，长江口地区受到越来越多人类活动的干预，航道整治、填海造陆和修建水库等大型工程改变了河口原有的动力条件，使得长江口径流条件发生了变化，对口门处的盐度锋产生一定的影响。锋面变化会对泥沙沉积、河口水质产生直接影响，进而对河口生态造成间接影响。目前，大多数对盐度锋的研究集中在锋面强度的变化及对物质输运的影响，而三峡工程改变了径流量的年内分配。本研究重点分析大通站实测径流量变化规律，并建立长江口平面二维水动力及盐度输运数学模型，研究长江口4支平面盐度锋对径流量变化的定量响应关系。

1 研究方法及模型设置

1.1 研究方法

研究区域如图1所示。沿长江口南槽、北槽、北港及北支深泓线分别确定一条纵剖面（见图2），各纵剖面起点均位于南北支分汊处（0 km里程点位置），其中北港与南北槽纵剖面在南支重合（0～40 km），南槽与北槽纵剖面在南支及南港部分重合（0～70 km）。盐度锋强度hHgs以盐度梯度表示，根据公式hHgs=Δs˙/Δx（Δs˙为Δx距离盐度变化）计算，以hHgs的最大值作为各支盐度锋所在的位置。若一个纵剖面上出现多个盐度梯度的峰值，则从南北支分汊处向下游依次为第一锋面、第二锋面，并以盐度梯度最大的锋面作为主锋面。

图1 研究区域（高程等值线，单位：m）Fig.1 Study area(elevation contour,unit:m)

图2 纵剖面及观测站点分布Fig.2 Longitudinal profile and distribution of observation stations

基于MIKE21软件建立了长江口平面二维水动力和盐度输运数学模型。MIKE21是由丹麦水动力研究中心（Danish Hydraulic Institute）开发的一款模拟内陆河流及海洋动力的数模软件。本研究中采用水动力（HD）模块对长江口平面二维潮流及盐度输运进行模拟，具体控制方程如下所示［12］：

潮流控制方程为

式中：t为时间；x、y为笛卡尔坐标；h为总水深，h=η+d，其中η为水面高程，d为静水深；S为源（汇）流率；分别为x、y方向的垂向平均流速分量；f为柯氏力参数，f=2Ωsinφ，其中Ω为地球自转角速度，φ为地理纬度；g为重力加速度；ρ为水的密度；ρ0为水的参考密度；P为大气压力；us、vs为源（汇）流向外界的速度分量；τsx和τsy为水体表面切应力分量；τbx和τby为底床切应力分量；Txx、Txy、Tyy为侧向切应力分量。

盐度输运扩散方程为

1.2 计算范围及模型设置

模型计算范围为西起江阴（长江）及仓前（钱塘江）（东经120.0°），东至东经125.5°，距长江口门约500 km；南起温州以南（北纬27.0°），北至江苏盐城以北（北纬34.3°），涵盖整个长江口、杭州湾及舟山群岛。模型采用无结构三角形网格（见图3），网格节点数为46 066，单元数为89 710。为确保计算精度及计算效率，网格分辨率由远海边界向近岸逐渐加密，其中北槽区域工程复杂、结构物细长，故对该区域进行局部加密，最小网格为10 m，最大网格为33 000 m。

图3 计算网格Fig.3 Computational grid

模型外海边界均采用由潮汐调和常数计算的潮位过程进行控制，2条河流开边界分别为江阴及仓前。大通站为长江潮区界控制站，江阴站为长江潮流界控制站，潮区界与潮流界之间不受潮流影响，大通站具有最长期的实测资料。江阴边界采用当年的大通站径流量进行设置，而钱塘江径流量较小，故仓前边界按照钱塘江多年平均径流量取整1 000 m3·s-1进行设置。上游边界盐度设为零，外海开边界盐度根据国家海洋科学数据中心的实况分析数据给定。表面风场采用欧洲中期天气预报中心分析产品ERA5提供的海面10 m处风速进行设定。模型计算时间步长在0.01～10 s内自动调节，克朗数小于1即可，故设置为默认值0.8。模型采用干湿动边界处理技术，干临界水深为0.005 m，湿临界水深为0.050 m。水平涡黏系数通过Samagorinsky亚网格尺度模型进行计算，Samagorinsky系数设为0.28，模型糙率采用曼宁数，数值范围设为60～98。

1.3 模型验证

模型潮位验证采用绿华山潮汐表潮位数据，从2014年7月1日00∶00至16日00∶00。流速及流向验证采用3个观测点流速流向数据，从2014年2月28日04∶00至3月1日04∶00。盐度验证采用S1观测点的大、小潮盐度数据，大潮从2014年7月13日15∶00至14日15∶00，小潮从2014年7月20日08∶00至21日08∶00，验证结果如图4所示。

图4 潮位、潮流及盐度验证Fig.4 Verification of tidal level,tidal current and salinity

为定量评价模型模拟结果的优劣，选用Willmott［13］提出的Skill法对模型进行效率评价。Skill法的具体方程为：

式中：SSkill为Skill数；M为模型计算值；D为实测值；为实测平均值；N为样本数量。当SSkill为1.00时，表示模型计算值和实测值完全一致；当SSkill大于0.65时，表示模型计算结果为“极好”；当SSkill在0.65至0.50之间时，表示模型计算结果为“非常好”；当SSkill在0.50至0.20之间时，表示模型计算结果为“好”；当SSkill小于0.20时，表示模型计算结果为“差”。各测站SSkill值如表1所示，可见效率评价结果均为极好，表示模型能够良好地模拟实际情况。

表1 模型评价结果Tab.1 Model evaluation results

2 长江口盐度对三峡工程调度运行的响应特征

三峡水库的具体调度方案为：每年6月中旬至9月底，水库按防洪水位145 m运行；每年10月截流蓄水，将水位由145 m提高至175 m；每年11月一般维持正常蓄水位175 m运行，若来水量达不到发电标准，则水位逐步下降；每年5月底保证水库水位不低于155 m；6月上旬水位降至145 m［14］。本研究以2003年作为三峡大坝工程对径流量影响的分界点，统计了1950年―2018年大通站的月平均径流量，具体如图5和表2所示。

图5 三峡工程建成前后大通站月平均径流量变化Fig.5 Monthly average runoff change at the Datong Station before and after the Three Gorges Project was completed

表2 三峡工程建成前后大通站月平均径流变化Tab.2 Monthly average runoff change at the Datong Station before and after the Three Gorges Project was completed 单位：m3·s-1

由大通站月均径流量分析可知，三峡工程建成后径流量增加主要出现在12月至次年3月，其中3月增加最多，可达3 535 m3·s-1；径流量减少主要出现在4月―12月，其中10月减少最多，可达7 260 m3·s-1。年内径流量分布总体呈现季节性差异缩小、洪峰流量削减的特征。将三峡工程建成前径流量与三峡工程建成后径流量（见表2）下盐度时空变化进行对比，为保证盐度达到稳定，共计算14个月，其中第一个月和最后一个月分别为前一年的12月与下一年的1月，选取中间的12个月进行分析。为全面分析三峡工程影响下长江口盐度时空变化特征，选取全年（1月―12月）、冬季（12月―次年2月）及秋季（9月―11月）3个阶段，其中冬季与秋季分别对应径流量增加与减少最明显的2个季节，而全年则能反映长江口的总体变化趋势。

图6为三峡工程建成前后年平均盐度的变化特征。从图6可以看出，受三峡工程建成后年平均径流量降低的影响，长江口口门处的盐度升高，但各支盐度增加程度不同。南槽口盐度增加值最大可达1.0～1.3 psu，较三峡工程建成前增加约10%；北支中下游段盐度增加0.7～0.8 psu，增加约7%；北港受径流量变化影响最小，盐度仅增加约5%。图7为三峡工程建成前后冬季长江口盐度的变化特征。三峡工程建成后冬季长江口盐水入侵程度整体降低，其中变化最明显的是南槽、北槽，盐度降低0.5～0.9 psu，降低约8%；其次是北港口，盐度降低0.5～0.7 psu，降低约7%；最后是北支，降低0.3～0.6 psu，其中北支上游盐度降低明显，降低约6%。图8为三峡工程建成前后秋季长江口盐度的变化特征。三峡工程建成后，秋季南槽盐度依旧变化最明显，盐度增加1.0～2.4 psu，增加约23%；其次是北支中游段，盐度增加1.4～2.2 psu，增加约20%；最后是北槽与北港，盐度增加0.5～1.9 psu，增加约15%。

图6 三峡工程影响下长江口年平均盐度分布Fig.6 Annual average salinity distribution in the Yangtze River Estuary due to the Three Gorges Project

图7 三峡工程影响下长江口冬季平均盐度变化Fig.7 Average salinity change in winter in the Yangtze River Estuary due to the Three Gorges Project

图8 三峡工程影响下长江口秋季平均盐度变化Fig.8 Average salinity change in autumn in the Yangtze River Estuary due to the Three Gorges Project

3 盐度锋对径流量变化的响应特征

长江口盐度梯度的变化主要受径流及潮流控制，前述讨论的年平均盐度以及随季节变化的盐度平面分布，反映了径流和涨落潮流对盐度的共同影响。径流和涨潮流联合作用下，北港口门外盐淡混合水体明显向北移动；径流和落潮流联合作用下，北港和南北槽口门外盐淡混合水体明显向东南移动；落潮期间长江口门外盐淡混合水体向海输运更远，水平盐度梯度也比涨潮期间大。由于重点探究径流量变化对长江口4支盐度锋特征值的影响，因此本节中选择M2分潮作为外海边界驱动数学模型，减小不规则潮汐变化对盐度锋的影响。模型的计算时长为3个月，根据上海海事局编制的1972年―2018年《长江口潮汐表》［15］计算得到该时段的最大潮差为3.21 m。根据水利部1999年―2000年《水情年报》（http：//mwr.gov.cn），大通站枯季最低流量为8 100 m3·s-1，洪季最大流量为83 900 m3·s-1，故在模型中设置径流量范围为10 000～80 000 m3·s-1、间隔为5 000 m3·s-1共15种情景，模型的其他设置保持不变。分析盐度锋对径流量变化的响应特征时，为减少图形所占篇幅，仅绘出径流间隔为10 000 m3·s-1的8种情景。

3.1 南槽

图9为M2分潮驱动下南槽纵剖面盐度及其梯度对径流量的响应特征。从图9可以看出，南槽的盐度梯度沿纵向呈现出双峰结构，即南槽中上游的强锋面（主锋面）和南槽下游的弱锋面。随径流量的增加，第一锋面下移并逐渐与第二锋面合并。当径流量较小时（10 000 m3·s-1）盐水入侵较严重，南槽第一锋面非常强，盐度梯度达到0.92 psu·km-1，盐度为15.22 psu，并且第一锋面位置最靠上游（距起点95 km左右），第二锋面处于萌发阶段；当径流量为10 000～50 000 m3·s-1时，随着径流量的增加，第一锋面逐渐削弱并向外海移动，第二锋面逐渐增强但位置几乎不变，始终在距起点147 km附近，即主锋面由第一锋面向第二锋面转移，并且主锋面盐度逐渐降低；当径流量超过50 000 m3·s-1时，第一锋面已基本消亡，主锋面变为第二锋面，位置随径流量增加几乎无变化，此时第二锋面盐度在8 psu左右。

图9 径流量变化对南槽纵剖面盐度及其梯度的影响Fig.9 Longitudinal salinity and salinity gradient in the South Passage due to runoff change

3.2 北槽

图10为M2分潮驱动下北槽盐度及其梯度对径流量的响应特征。当径流量为10 000 m3·s-1时，北槽盐度锋存在双锋面结构，其中第一锋面盐度为8.07 psu，第二锋面盐度为21.30 psu。当径流量为20 000 m3·s-1时，双锋面结构消失，随着径流量的增加，北槽主锋面依然有从第一锋面向第二锋面转移并合并的趋势。当径流量超过20 000 m3·s-1时，北槽主锋面已经移动到第二锋面处；当径流量为30 000～50 000 m3·s-1时，北槽第二锋面强度维持在一定水平不变。然而，随着径流量进一步增大，主锋面（此时为第二锋面）强度及该锋面对应的盐度又开始降低，但位置始终没有发生明显变化。

图10 径流量变化对北槽纵剖面盐度及其梯度的影响Fig.10 Longitudinal salinity and salinity gradient in the North Passage due to runoff change

3.3 北港

图11为M2分潮驱动下北港盐度及其梯度对径流量的响应特征。从图11可以看出，当径流量为10 000 m3·s-1时，北港出现了微弱的双锋面结构，但当径流量增加到20 000 m3·s-1时，北港盐度锋的双锋面结构完全消失。根据对南槽、北槽低径流量条件下锋面结构的分析可以推断，当径流量小于10 000 m3·s-1时，北港是可以呈现双锋面结构的，但实际中长江上游径流量为10 000 m3·s-1时已经足够小了，再进一步减小径流量研究北港锋面变化的意义不大，因此认为北港盐度锋只有单锋面结构。北港盐度锋位置随径流量变化的响应微弱，基本停留在距上游130～140 km的范围内，但其强度却要比南槽、北槽锋面大很多，并且主锋面盐度随径流量的增大逐渐减小，变化范围为13.99～18.79 psu。当径流在50 000 m3·s-1以内时，北港盐度锋强度对径流量变化的响应较敏感；当径流超过50 000 m3·s-1以后，锋面强度基本不再随径流量的变化而变化。

图11 径流量变化对北港纵剖面盐度及其梯度的影响Fig.11 Longitudinal salinity and salinity gradient in the North Channel due to runoff change

3.4 北支

图12为M2分潮驱动下北支盐度及其梯度对径流量的响应特征。北支第一锋面对径流量变化响应十分强烈，当径流量只有10 000 m3·s-1时，北支第一锋面强度较大，盐度梯度可达1 psu·km-1以上，并且位于靠近上游的位置（距起点11 km），此时锋面对应的盐度为7.46 psu；当径流量增加至20 000 m3·s-1时，北支第一锋面强度急速下降，盐度梯度为0.36psu·km-1，锋面开始呈现波浪形态，位置仍处于上游（距起点13 km），盐度也随之降低至2.31 psu；随着径流量进一步增加至30 000 m3·s-1，第一锋面波浪形态依旧存在，强度降低至0.17 psu·km-1，并且第一锋面位置由第一波峰处（距起点13 km）转移至最后波峰处（距起点53 km），即从上游向中游移动；当径流量大于40 000 m3·s-1时，第一锋面的波浪形态基本消失，强度持续降低，锋面主要位于距起点58 km以外的位置。北支第二锋面随径流量变化特征与北槽第二锋面基本一致，当径流量在50 000 m3·s-1以内时，第二锋面强度随径流量增大而增加；当径流量超过50 000 m3·s-1时，第二锋面强度随径流量增大而减小，并且位置变化不明显，位于距起点109～113 km处，但第二锋面所对应的盐度随径流量的增加始终减小，由21.51 psu（10 000 m3·s-1）降低至8.64 psu（80 000 m3·s-1）。整体上，随径流量的增加，北支主锋面依旧由第一锋面向第二锋面移动并合并。

图12 径流量变化对北支纵剖面盐度及其梯度的影响Fig.12 Longitudinal salinity and salinity gradient in the North Branch due to runoff change

4 长江口盐度锋与径流量变化的定量关系

为探究各支盐度锋与径流量之间的定量关系，绘制15种径流量情景下长江口4支盐度锋特征值（位置、强度）与径流量的拟合函数（见图13～16）。利用判定系数R2进行拟合优度检验，R2越接近于1，说明拟合关系越好。

图13为南槽盐度锋特征值与径流量的拟合函数关系。南槽第一锋面位置与径流量成线性相关，R2为0.851，强度与径流量成二次函数相关，R2为0.916；南槽第二锋面位置与径流量之间的拟合结果相对差一些，R2为0.553，这可能是由南槽第二锋面位置基本不随径流量改变造成的，第二锋面强度与径流量成二次函数相关，R2为0.783。

图13 南槽盐度锋特征值与径流量的拟合函数Fig.13 Fitting function between salinity frontal eigenvalue and runoff in the South Passage

图14为北槽盐度锋特征值与径流量的拟合函数关系。由于北槽盐度锋第一锋面在径流量超过20 000 m3·s-1时就已经消失，因此仅对第二锋面的变化特征进行拟合。北槽第二锋面位置与径流量成线性相关，R2为0.814，强度与径流量成二次函数相关，R2为0.829。

图14 北槽盐度锋特征值与径流量的拟合函数Fig.14 Fitting function between salinity frontal eigenvalue and runoff in the North Passage

图15为北港盐度锋特征值与径流量的拟合函数关系。北港盐度锋为单锋面结构，锋面位置与径流量之间成线性相关，R2为0.764，强度与径流成二次函数相关，R2为0.745。

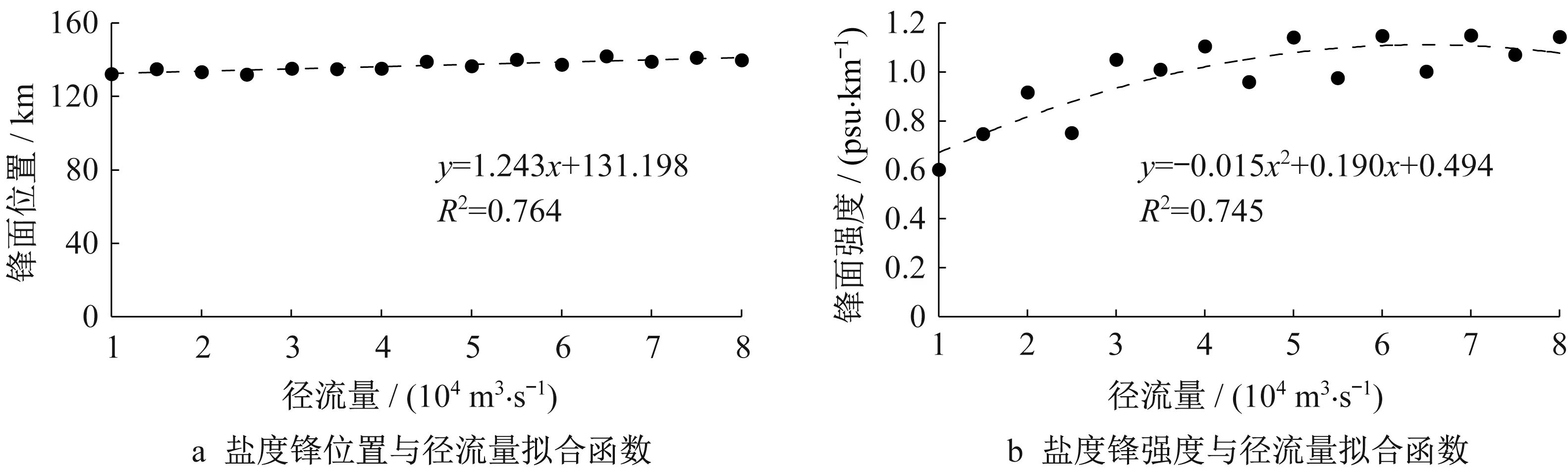
图15 北港盐度锋特征值与径流量的拟合函数Fig.15 Fitting function between salinity frontal eigenvalue and runoff in the North Channel

图16为北支盐度锋特征值与径流量的拟合函数关系。由于北支盐度锋的第一锋面存在波浪形态，并且随径流量增加有从第一波峰向最后一波峰移动的趋势，同时第一锋面位置随径流量增加出现突变的情况。经拟合，第一锋面位置与径流量成线性相关，R2为0.839，强度与径流量成二次函数相关，R2为0.894。北支第二锋面位置与径流量之间成线性相关，R2为0.628，强度与径流量成二次函数相关，R2为0.749。