循环荷载下粉土中吸力基础承载特性试验研究

马士力，谢立全

（同济大学土木工程学院，上海 200092）

较之陆上风电，海上风能资源丰富，而且沿海地区电网容量大、风电接入条件好，因此海上风电更具优势。据估计，在海上风电场项目中风力发电机基础的建设成本约占总成本的25%～35%［1-2］。吸力基础作为新型风电基础形式，是一种顶部封闭下端开口的钢制或钢-混结构圆桶基础，因其具有节省投资、缩短安装工期、可重复利用等优点，在海上风电工程中逐渐受到重视［3-4］。2020年国内首台海上风力发电机吸力基础顺利应用于广东省阳江市阳西沙扒300 MW海上风电项目，该基础的应用有效降低了工程施工对海洋环境的污染，并减小了海上施工风险［5］。

吸力基础在服役期间受到风浪流等循环荷载的作用，而长期的桩-土循环荷载容易导致吸力基础水平承载性能劣化。对于风力发电机基础，应着重考虑低竖向力和高水平荷载的共同作用［6］，因此基础的水平承载力和刚度是设计的主导因素［7］。关于砂土和黏土中吸力基础与桩周土体水平单调相互作用已有大量的研究［8-11］。Bhattacharya［1］发现，海上风力发电机在25年的服役期内将经历107～108次的加载循环，这将导致基础不可恢复的转动。Cox等［12］、Kelly等［13］和Bienen等［14］通过1g小模型试验与离心机试验探讨了循环荷载下吸力基础的承载特性，发现吸力基础的累积水平位移和沉降量随循环次数的增加而增加，累积转角也随着循环次数的增加而增加，并存在幂指数关系。利用模型试验，罗仑博等［15］发现水平循环荷载下桩周土趋于致密化，导致砂土地基中吸力基础的水平承载力增加。目前我国许多近海风电场和潜在海上风电场场址土层大部分为粉土［16］，而吸力基础承载特性研究大多集中在砂土和黏土，因此研究循环荷载下粉土中吸力基础承载特性有着极其重要的意义。

针对我国东海海域粉土进行了一系列的1g模型试验，研究了循环荷载下吸力基础水平承载特性，并对试验结果进行了量纲一处理。通过吸力基础的循环荷载-转角响应，得到了吸力基础水平刚度与水平转角之间的关系。基于试验中吸力基础的累积转角，分析了其与循环次数之间的关系，并预测了吸力基础服役期累积转角的变化。最后，探究了循环荷载下吸力基础内部的压强变化，并重新构建卸载刚度，以进行对比分析。

1 1g模型试验装置和流程

1.1 试验装置

试验在砖-混模型箱内完成。模型箱内部尺寸为1.72 m×0.76 m×0.72 m（长×宽×高），壁厚为17.20 cm。模型箱内底部铺设的约5 cm厚的碎石垫层用作排水通道，土体与碎石垫层之间采用土工布进行分隔。模型箱外设水箱系统，用于反渗饱和土体［17］和调节模型箱内水位高低［16］。试验装置示意图如图1所示。

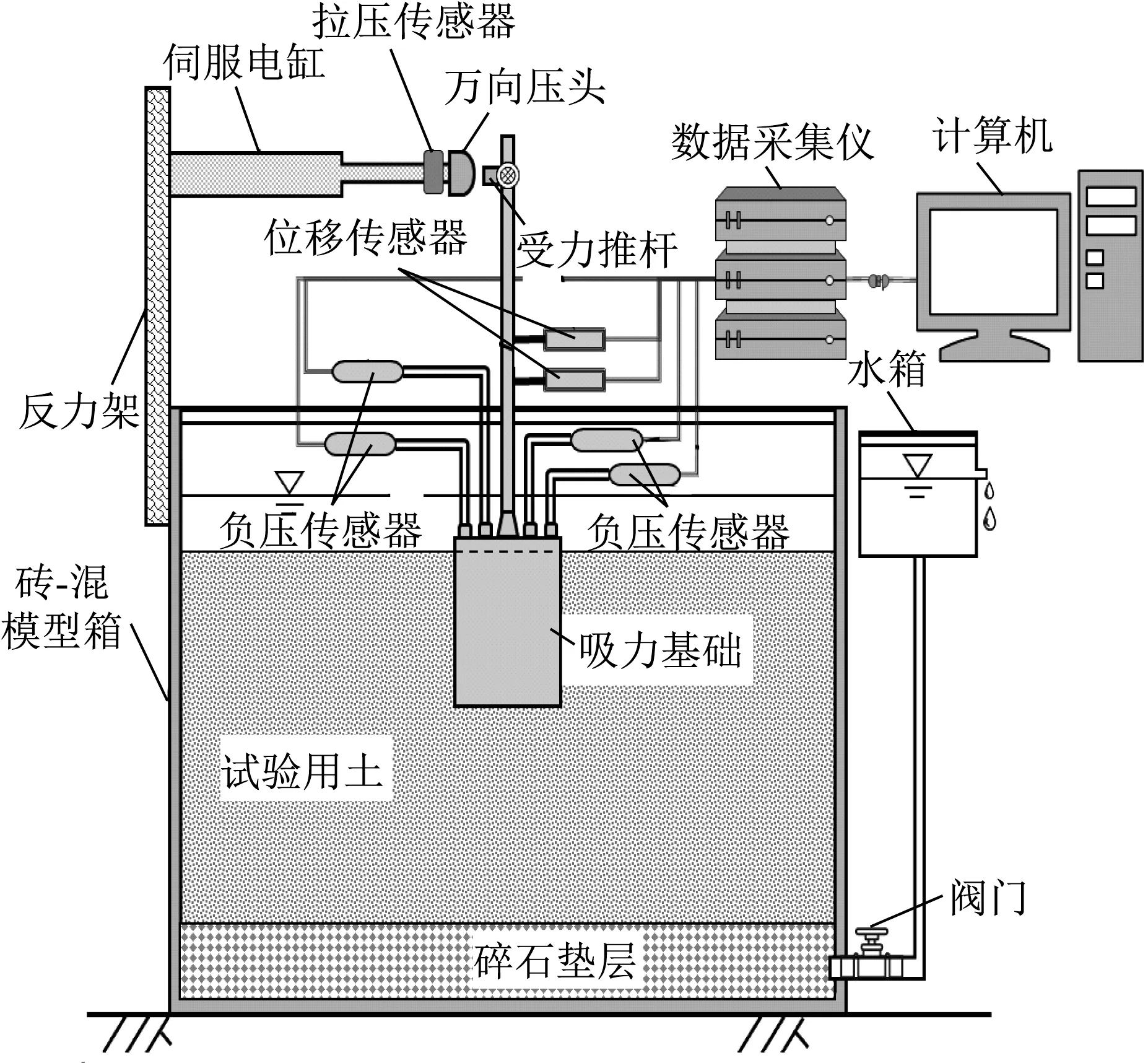
图1 试验装置示意图Fig.1 Schematic diagram of test set-up

吸力基础由不锈钢制成，桶壁和顶板厚度分别为2 mm和10 mm，长径比L/D=1.5，具体尺寸如图2所示。吸力基础顶板设有4个直径为8 mm的排水孔，并与负压传感器连接，排水口1、2、3、4处测得的压强分别为p1、p2、p3和p4。图2中，h为转动中心位置。顶板非密封状态时排水口打开，不与负压传感器相连。如图1所示的伺服电缸固定于钢制反力架上，提供稳定的水平循环荷载。循环荷载加载方式如图3所示，加载频率为0.05～0.02 Hz，该频率适合于Bhattacharya等［18］得到的Jonswa谱波浪，荷载沿模型箱长度方向施加，以避免边界效应影响。作为海上风电机组的重要组成部分，吸力基础荷载作用点一般大于3倍桶高［12］，本研究中水平荷载加载高度e=540 mm（3L）。位移传感器和负压传感器分别与动态数据采集仪相连，数据采集频率为10 Hz。

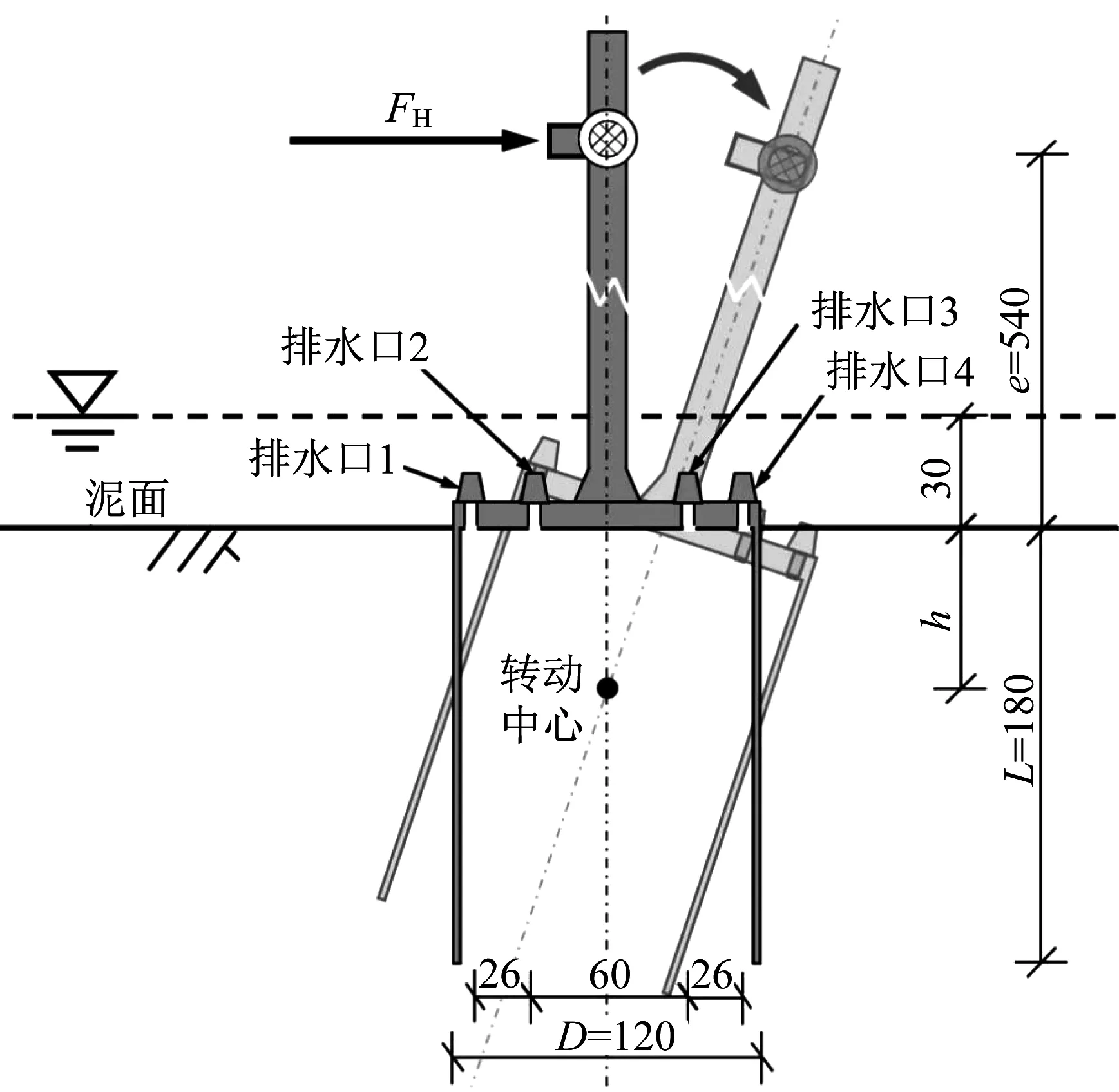
图2 吸力基础模型（单位：mm）Fig.2 Suction caisson model(unit:mm)

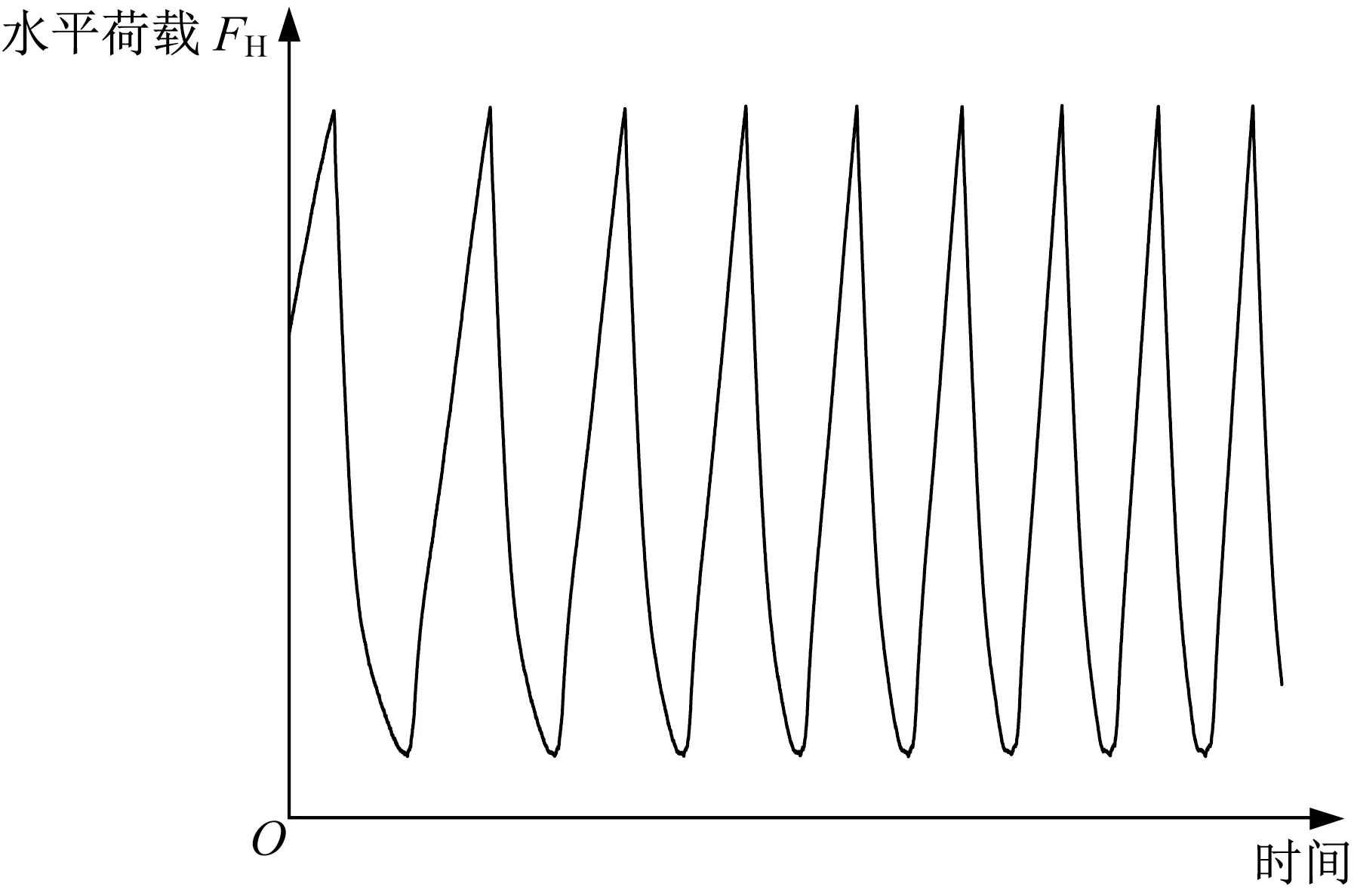
图3 水平荷载加载示意图Fig.3 Schematic diagram of horizontal loading

试验用粉土（见图4a）取自上海东部近海，其颗粒级配如图4b所示。采用堆载预压法制备粉土试件，在堆载预压的同时进行反渗饱和，并持续24 h左右，最终土层厚度达0.6 m。水箱系统中调整后水位高于泥面约3 cm。粉土试件饱和重度约为19.6kN·m-3，含水率为17.8%～23.5%，渗透系数为1.62×10-6m·s-1。对3组粉土试件进行单桥静力触探试验，所得比贯入阻力曲线如图5所示。从图5可见，制备的粉土试件具有较好的一致性。

图4 试验用土及其颗粒级配曲线Fig.4 Silt in tests and its particle grading curve

图5 单桥静力触探试验曲线Fig.5 Curves of single bridge cone penetration tests

1.2 试验理论与流程

LeBlanc等［19］和Zhu等［20］定义了2个量纲一参数ξb与ξc，分别表征循环荷载的幅值大小和对称性，即：

式中：Mmax、Mmin分别为一个周期内作用于基础上弯矩的最大值与最小值；FH，max和FH，min分别为一个周期内作用于基础上水平作用力的最大值与最小值；Mult和FH，ult分别为相同加载速率的单调荷载下基础所能承受（容许）的极限弯矩和极限水平荷载。

图6为循环荷载下吸力基础的累积转角-荷载关系，最大、最小循环荷载对应的累积转角分别为θmax，N和θmin，N。为评价循环作用下吸力基础累积转角的演化，LeBlanc等［19］将累积转角量纲一化，计算式如下所示：

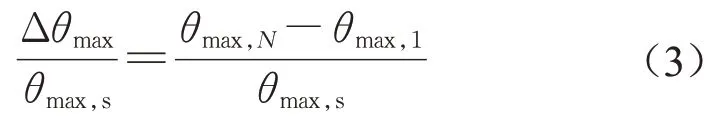
式中：θmax，s为静力加载时吸力基础最大循环荷载对应的水平转角，θmax，s=θmax，1。

若在服役期间海上风机基础刚度发生改变，则结构的一阶固有频率也发生变化，从而改变了结构的固有频率。Zhu等［21］和LeBlanc等［19］定义了卸载刚度k′N（kN·m-1，见图6），但在荷载对称性系数ξc≠0时，k′N数值较大，不利于对比分析，因此定义卸载刚度kN。虽然水平位移对吸力基础的性能有重要影响，但是结构的动力特性很大程度上取决于吸力基础的刚度。Wang等［7］提出水平刚度K（即水平荷载与相应水平位移的比值）以分析吸力基础水平运动过程中的刚度变化。为消除尺寸效应对试验结果的影响，采用量纲一参数进行数据分析，如表1所示［20，22］。表1中，pa和γ′分别为大气压强和土体的浮重度。

表1 吸力基础在1g模型试验中的量纲一参数Tab.1 Normalized parameters for a suction caisson in 1g model tests

图6 累积转角和卸载刚度定义Fig.6 Definition of accumulated rotation and unloading stiffness

粉土试件制备完成后，以0.1 mm·s-1匀速将吸力基础竖直压入土体［23］。在循环试验前进行相同加载速度下的单调水平承载力试验，顶板密封与非密封状态下极限承载力分别为30.7 N和28.3 N（见图7）。将伺服电缸、负压传感器与位移传感器安装到位后静置试验系统1 h，设置逻辑控制器参数ξb与ξc，控制水平循环荷载动作（试验方案如表2所示），打开数据采集仪后开始试验。

图7 单调荷载作用下水平荷载与转角关系Fig.7 Relationship between lateral load and rotation under monotonic loading

表2 试验方案Tab.2 Experimental scheme

2 试验结果与分析

2.1 循环加载响应分析

图8、9分别为吸力基础的循环荷载-水平转角响应曲线和水平刚度-水平转角响应曲线。从图8可以看出，在加载初期，吸力基础周围粉土变形近似弹性，循环荷载曲线几乎呈线性增大，此时荷载增加较快，水平转角变化较小，水平刚度约为450。当荷载超过一定值后，水平刚度急剧变小。从图9可以看出，由于吸力基础周围粉土的变形而使得水平位移增大，水平荷载为FH，max时水平刚度随着循环次数的增加而减小［7］。对比B4C和B4CU，在非密封状态下，首次卸载残余转角较大，而在密封状态下，由于加载过程中吸力基础顶板与土体分离而使得桶内形成负压，此负压有利于吸力基础的“复位”，因此密封状态下首次卸载残余转角较小。由于负压的存在，随着循环次数的增加桶-土密封空间逐渐被水体占据，桶内负压减小导致密封状态下残余转角产生相对较大的变化。如图8所示，ξc=0时第1次卸载后残余转角随着ξb增大而减小，ξb=0.6时的残余转角是ξb=0.2时的4.07倍。B6C与B6C33在第10次加载峰值时水平刚度相差仅4.7%，荷载对称性ξc对水平刚度的影响不显著。

图8 循环荷载-水平转角响应Fig.8 Cyclic loading-lateral rotation response

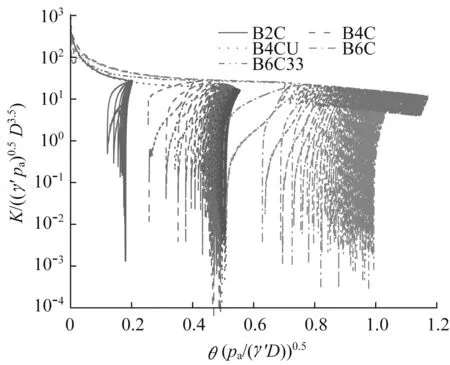
图9 水平刚度-水平转角响应Fig.9 Lateral stiffness-lateral rotation response

2.2 吸力基础累积转角

图10为累积转角Δθmax/θmax，s与循环次数N的关系曲线。可以看出，累积转角随着循环次数的增大而增加。在初始阶段，Δθmax/θmax，s快速积累，并随着循环次数的增大而增量逐渐减缓。对比B2C、B4C和B6C，Δθmax/θmax，s增长速率随着ξb的增加而增大。循环次数N=50时，B6C的累积转角比N=10时增长了53.6%。对比密封和非密封状态，非密封状态时没有顶板负压耗散影响，B4CU的累积转角随着循环次数的增大迅速增加而后趋近某一稳定值。B6C33累积转角增长速率明显高于B6C，循环60次时ξc=0.33和ξc=0的 增 长速率分别 为0.003 3和0.001 7。

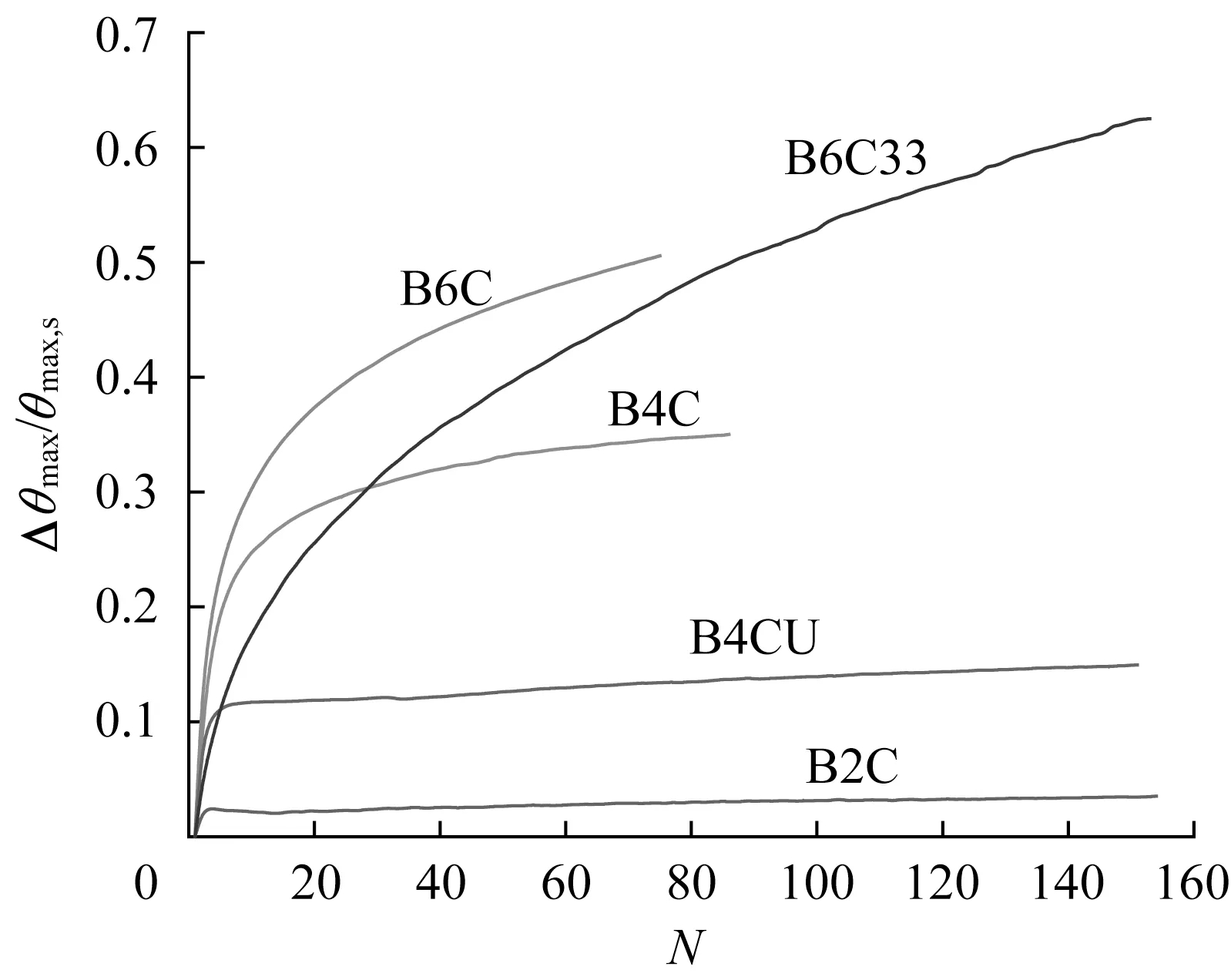
图10 累积转角和循环次数关系Fig.10 Relationship between accumulated rotation and number of loading cycles

通过大量试验对单桩和吸力基础累积转角与循环次数的关系进行研究，Zhu等［20，24］和Cox等［12］提出了幂指数关系，如下所示：

式中：α和β为量纲一变量。表3为通过回归方程得到的量纲一变量α和β。Zhu等［20］在松散和干燥的粉土中对吸力基础进行水平循环荷载的1g模型试验，得到α=0.39，而Foglia等［25］得到致密砂中α=0.18。B2C、B4C、B4CU和B6C的α为0.180～0.390，而B6C33相对较大，为0.449。β与ξb的关系如图11所示。可以看出，Cox等［12］通过离心机得到ξb=0.54时β相对较小，仅为0.032。试验中ξc=0.33时的β低于ξc=0时的β，而Zhu等［24］得到ξc=0.1时β相对较大。ξc=0、ξb=0.20～0.62时通过拟合本研究试验数据和Zhu等［20］研究结果可以得到以下计算式：

图11 β与ξb的关系Fig.11 Variation of β with ξb

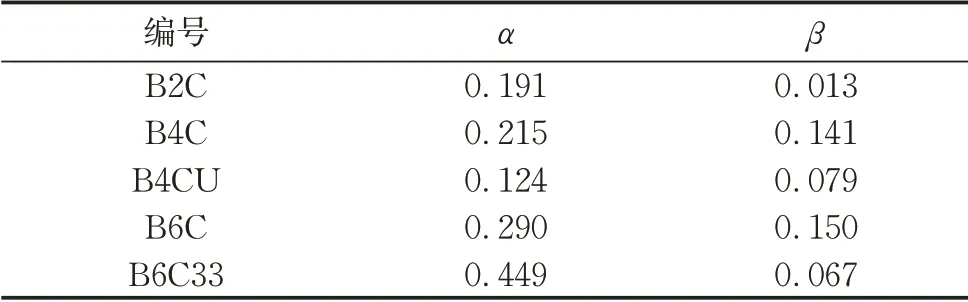
表3 变量α和β值Tab.3 Values of α and β

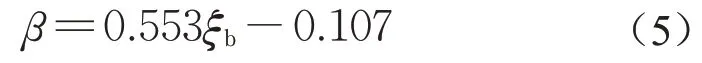
海上风力发电机15年服役期（循环次数约4×107）［11］时，ξb=0.5和ξc=0下，由式（4）和式（5）可得累积转角为3.96。若设计中规定吸力基础水平转角最大值为0.250°时，基础受到0.5Mult，则理论上首次加载水平转角应小于0.063°。

2.3 桶内压强与水平转角关系

为研究加载过程中桶内压强对吸力基础周围粉土的影响，参考沉贯过程归一化速度V［26-27］。V可以表达为

式中：v为加载速率；cv为垂直固结系数，对于黏土cv=2.6 m2·a-1，对于砂cv至少为60 000 m2·a-1［28］。Chung等［29］认为，V＞30时土体处于完全不排水状态，而当V＜0.01时土体处于完全排水状态。本研究中循环试验加载点速度为0.1 mm·s-1，为简便计算，假定转动中心在吸力基础顶板中心处，吸力基础顶板最大运动速度约为0.011 mm·s-1。试验中粉土渗透系数较小，偏于黏土，取黏土cv可得V=0.016。由此可见，桶内土体处于部分排水状态，因此容易导致循环加载初始阶段桶-土之间密封空间出现负压而形成较大的水平刚度（见图12a）。随着循环次数的增加顶板与土体之间出现存积海水现象（见图12b），海水的不可压缩性与土体较小的渗透共同作用使累积转角增大（见图12c）。吸力基础顶板排水孔处桶内压强与水平转角的关系如图13所示，图中正值表示负压（小于大气压强）。循环加载初期顶板挤压桶内土体造成桶内出现了正压；初始循环加载下B2C较小的水平转角和桶体挤压土体排水共同作用导致桶内压强基本保持正压。循环加载初期随着水平转角的增大，顶部与土体进一步分离，空间变大（见图12），压强减小并逐渐趋于负压，增大了吸力基础抗倾覆能力。负压引起吸力基础周围土体排水，水体逐渐占据桶-土密封空间，桶内负压减小。从图13可以看出，桶内压强变化范围随着ξb的增大而增大，并随着循环次数的增加而小，桶内压强对抗倾覆能力影响越来越小。当ξb=0.6、ξc=0，循环次数N=5加载和卸载时p1分别为0.002 5和-0.003 1。对于B6C，加载时p1、p2、p3、p4呈现先增大后减小的趋势；对于B6C33，卸载时p4随着循环次数增大而增加。

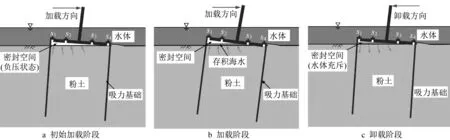
图12 循环加载下吸力基础与土相互作用示意图Fig.12 Schematic diagram of interaction between suction caisson and soil under cyclic loading

图13 桶内压强与水平转角关系Fig.13 Relationship between pressure in suction caisson and lateral rotation

2.4 转动中心位置

假定转动中心在吸力基础的中轴线上，如图2所示，转动中心位置h可以表示为

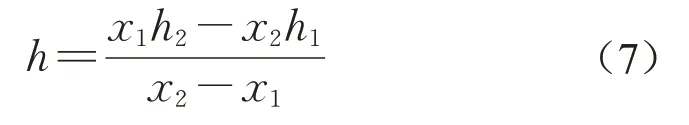
式中：h1和h2为位移传感器距顶板高度；x1和x2为位移传感器得到的位移值。

图14为循环荷载下吸力基础转动中心位置与水平转角关系，其中负值表示转动中心在顶板上方。ξc=0时B6C的h/L相对较大，而且主要移动范围为0.47～0.61。非密封状态加载时转动中心位置与密封状态近似。B6C33的转动中心在0.1附近，h/L较小容易造成吸力基础承载能力的下降，因此长期循环荷载作用下B6C累积转角将小于B6C33。无论是加载还是卸载h/L都有明显减小趋势，此现象将加速吸力基础倾覆。

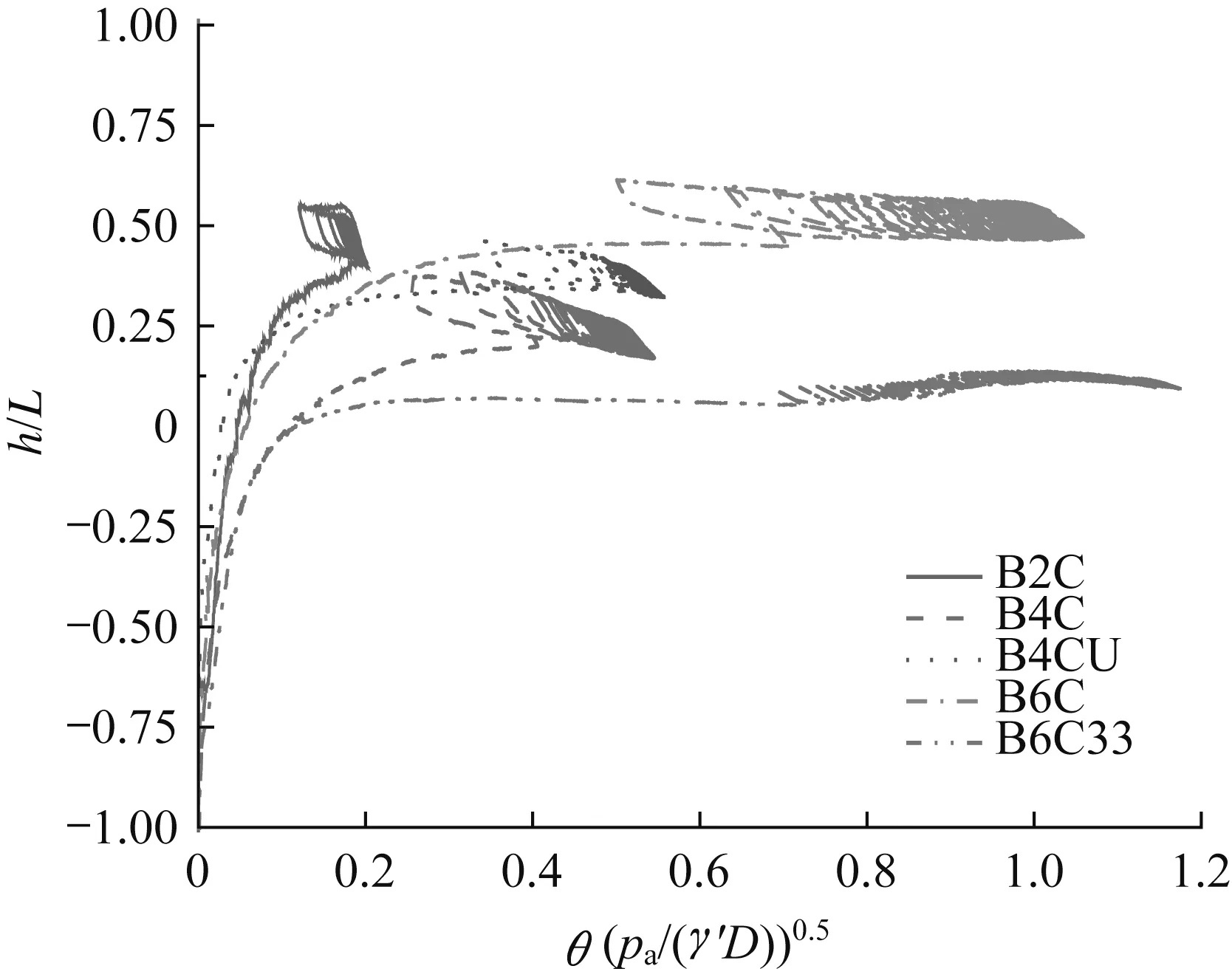
图14 转动中心与水平转角关系Fig.14 Relationship between location of rotation center and lateral rotation

2.5 卸载刚度

Arany等［30］通过计算发现，如果卸载刚度增长50%，风力发电机固有频率就会变化1.5%～3.5%，因此研究卸载刚度的变化对海上风力发电机稳定性设计尤为重要。吸力基础卸载刚度与循环次数关系如图15所示。卸载刚度随着循环次数N的增大而增大并遵循对数关系，这与Cox等［12］得出的结果相同。随着土体固结和越来越致密，卸载刚度逐渐趋于稳定。

图15 卸载刚度与循环次数关系Fig.15 Relationship between unloading stiffness and number of loading cycles

ξc=0时B4C的k/（（γ′pa）0.5D3.5）相对较小，当N=50时B4C的卸载刚度仅为B2C的71.06%和B6C的86.83%。由于卸载不完全B6C33卸载刚度相对较大且不稳定，但也存在与B6C相同的增长趋势。当循环次数N=32时，B4CU的卸载刚度达到最大值后呈现下降趋势，这是因为吸力基础土体受到循环荷载作用后出现了软化。ξc=0时吸力基础的卸载刚度平均增长了3.73倍，可见粉土对风力发电机服役期的固有频率和稳定性有着重要影响。

3 结论

（1）吸力基础周围粉土变形显著，致使吸力基础水平位移增大，并且其最大水平荷载FH，max对应的水平刚度随着循环次数的增加而减小。非密封状态下吸力基础的首次卸载残余转角较大，而密封状态下加载过程中吸力基础顶板与土体分离使得桶内形成负压，负压有利于吸力基础的“复位”，因此密封状态下首次卸载残余转角较小。

（2）在初始阶段吸力基础水平转角快速积累，并随着循环次数的增大而增量逐渐减缓。当ξc=0时，Δθmax/θmax，s增长速率随着ξb的增加而增大。当桶内土体处于部分排水状态时，容易导致循环初始阶段吸力基础水平刚度较大。随着循环次数的增大顶板与土体之间出现存积海水现象，海水的不可压缩性与土体较小的渗透性使得土体卸载不彻底，继而增大累积转角。

（3）无论是加载还是卸载，吸力基础转动点均呈明显的上移趋势，此现象加速了吸力基础的倾覆。卸载刚度随着循环次数的增大而增大并遵循对数关系。随着土体固结和致密，卸载刚度逐渐趋于稳定。

作者贡献声明：

马士力：试验设计，试验实施，结果分析，论文撰写与修改。

谢立全：方案讨论与优化，论文修改。