耦合腔系统中Bose-Hubbard模型与稳态制备的理论研究
2022-11-07平一凡刘忠菊
平一凡,杨 青,刘忠菊
(沈阳工业大学 理学院,沈阳 110870)
量子信息是量子力学与信息学相结合的交叉性学科,充当着扩展与完善经典信息的角色[1]。近年来,国内外学者以“量子编码”为切入点,逐步扩展到对量子隐形传态[2]、量子计算、量子度量学和量子模拟等热点分支的研究中。从“激光冷却和捕获原子”到“墨子号-星地双向纠缠”[2-3]与“远距离量子隐形传送”,再到2021年的九章量子模拟原型机,量子信息在实现信息传输更安全、计算模拟更快速和微弱测量更精密等方面已展现出广阔的应用前景,正引领着全球的科技革命。当然,该领域飞速发展离不开量子力学和量子光学等理论体系的支撑[4-5],如在量子信息背景下,进行量子隐形传态实验的前提正是建立在利用量子光学中参量下转换非线性光学过程这一基础之上。
量子光学与原子分子物理领域碰撞衍生出腔量子电动力学(即腔QED系统),其工作原理是将束缚在高品质腔中的原子或离子与腔中光场相互作用,从而实现量子信息处理的过程[6]。实验中,因受较小的格点距离和较短的相干时间等因素的限制,致使很多微观的量子现象难以观测,腔QED系统因其优越的量子相干性,恰能有效解决这一问题,因此被用作量子模拟现象的有效平台。另一方面,为了实现分布式量子计算[7],以及在强关联多体系统的研究中对多个量子比特的操控模拟,1997年Pellizzari T首次建立了耦合腔模型(即将多个分离的腔系统耦合起来)。研究发现,以玻色为媒介耦合两光腔系统[8]可分别使被囚禁在2个腔中的原子产生纠缠及实现量子态的转移,因此,耦合腔系统可为模拟强关联多体系统提供有效的资源平台。Ye等[9]提出了利用光纤耦合腔系统产生两原子纠缠态的方案;Zheng等[10]提出了产生双模压缩态的方案;Zhong等[11]提出了利用两维耦合腔系统实现多原子相干耦合的理论方案等。作为量子计算和量子模拟最具前景的物理系统之一,耦合腔系统已经成功应用于多量子体系等信息传输及处理中,实现了量子信息网络化。
近年来,腔QED系统中Bose-Hubbard模型表现出空前的实用性。如耦合腔列系统的Bose-Hubbard模型展现出绝缘相到超流相的量子过程,显示出独特的量子特性。本文也将运用Bose-Hubbard模型,通过绝热剔除方法得到光子的有效哈密顿,研究在两腔耦合系统中的量子性质及稳态制备过程。
1 模型
本文选取单模光腔系统。如图1所示,在腔内放置一个四能级原子,原子与光场发生相互作用,系统存在2种耗散情况,即原子能级跃迁可能产生自发辐射耗散,以及腔内光子也会发生泄露耗散。图中κ为腔模的泄露率,γ为原子处于激发态的衰减率,本文后面在处理有效哈密顿时,绝热剔除掉原子的自由度,因此,对于原子能级的衰减不予考虑了,只讨论了腔模泄露对稳态输出的影响。四能级原子具有电磁诱导透明效应,原子与腔场之间的耦合及原子的跃迁行为如下:|a>表示原子的基态,|c>为亚稳态,|b>和|d>表示原子的激发态;腔模分别与|b>↔|a>与|d>↔|c>之间的跃迁产生耦合,耦合系数分别为g1、g2,|c>↔|b>的跃迁为经典泵浦场驱动原子的跃迁,Ω表示泵浦场的Rabi频率,Δ和δ表示失谐量。

图1 单模光腔系统示意图与四能级原子结构图
系统的哈密顿由自由哈密顿和相互作用哈密顿组成,在旋波近似的条件下,可以写出该模型中系统的自由哈密顿量为

此时腔中相互作用哈密顿量可以写作HI=H1+H2,
其中

式中:a+、a表示腔场的产生、湮灭算符,在强场驱动的情况下,也就是当两态被外场以较大的强度耦合在一起,组成了缀饰态,利用H1作用在|b>和|c>两态上,得到缀饰态哈密顿的矩阵形式,很容易得出缀饰态H1的本征态和本征值

将式(4)代入到式(2)中可得

接下来,把变换后的哈密顿作幺正变换到缀饰态绘景下,即H3=eiH1tH2e-iH1t,同时考虑>>g2的情况,可以利用绝热剔除方法,将上式中的缀饰态剔除掉,得到
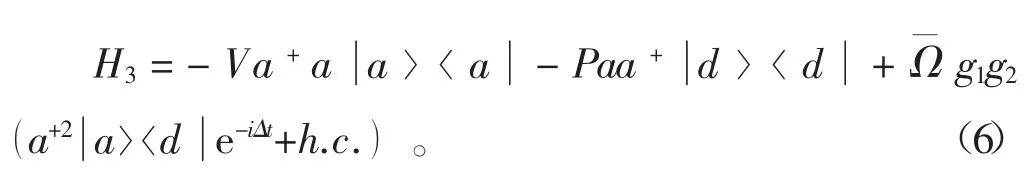
令原子的初态不处于缀饰态中的2个态上,同时观察到式(6)中的前2项是基态和激发态的斯塔克位移,后2项则表示原子在基态和激发态之间的跃迁。因为则可以令原子的初态处于基态上,再次利用有效哈密顿的方法进行绝热剔除掉激发态,得到最终有效哈密顿量的表达形式为

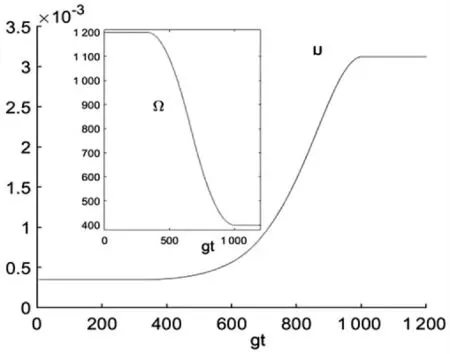
图2 在位势U关于经典场的变化
2 数值模拟
为了研究系统的稳态的制备,考虑两腔耦合系统模型如图3所示,两腔之间的耦合通过光子的跳变来实现,J为相邻两腔耦合的跳变强度,同时唯象地加入2个光腔中A模光场的泄露项根据已经得出的单腔中的有效哈密顿,耦合腔系统的哈密顿可以写为
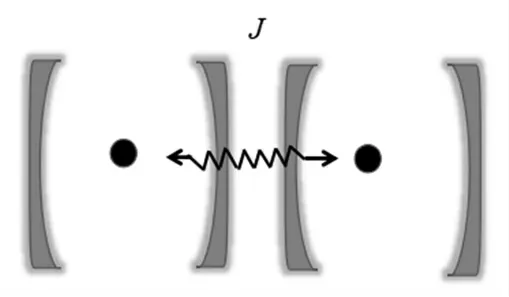
图3 耦合腔系统。因相邻腔光模重叠而发生光子跳变

接下来,通过数值模拟来考察系统的稳态制备过程,同样控制随时间的变化时,系统参数Rabi频率发生变化,通过Rabi频率的变化,系统的平均光子数N=

图4 平均光子数N随时间的变化
为了讨论两腔之间的非局域特性,接下来讨论两腔之间的量子纠缠,在耦合腔哈密顿的基态下,选用Von Neumann熵作为量子纠缠的度量,两体之间的熵的定义式为

式中:ρA=TrB(ρAB)为系统的约化密度矩阵。
绘制了两腔之间的基态纠缠熵关于失谐量Δ的变化图像,如图5所示,可以看出,当失谐量较小时,熵随着Δ的增大而陡增,在Δ=2g附近达到最大值,然后随着Δ的增大开始减小;同时,又改变经典场Rabi频率为Ω,显然,在相同失谐量Δ的状态下,Ω越大,纠缠越大。这是由于当Ω增大时,单个光腔中的在位势减小,光子在单个光腔中体现出较弱的非线性,也就是说单个光腔中局域性变得越来越弱,同时,光子在两腔之间非局域行为越来越明显,即基态纠缠熵增大。
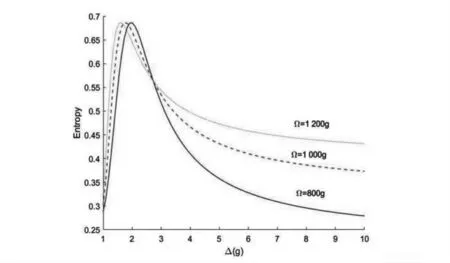
图5 两腔之间的纠缠熵随失谐量Δ的变化
3 结论
本文对耦合腔QED系统进行了理论研究,在大失谐的情况下,利用绝热剔除法,在单腔中得到关于光子的非线性有效Bose-Hubbard哈密顿量,通过对在位势随拉比频率变化的研究,分析了所得哈密顿的有效性。
通过改变经典场拉比频率进行量子操控,结果发现,令系统的初态是真空态,在拉比频率由小变大的过程中,系统经历了由真空态向稳态的制备过程,并分析了拉比频率和在位势在稳态输出过程中扮演的角色,同时,还唯象地加入系统的耗散,观察到腔场泄露率是影响稳态输出的不利因素,目前高Q腔可以解决这一问题;同时又研究了两腔之间的非局域特性,数值解析结果给出了两腔之间基态量子纠缠何时达到最大值,并分析了经典场Rabi频率在控制纠缠输出中起到的作用,以上结论可以为量子信息过程提供有效的模拟平台。
