基于改进HHT的电缆故障定位研究
2022-11-07丁希鹏蔺怡于浩
丁希鹏 蔺怡 于浩
(安徽理工大学电气与信息工程学院,安徽淮南 232001)
0 引言
行波测距法是目前对电缆故障测距的主要方法。文献[1]利用小波包的消噪方法对得到的信号进行处理分析,但在使用小波包方法时需要人为设定选取分解层数,可能会产生较大误差。文献[2]利用HHT对故障行波信号进行处理分析,通过瞬时能量谱来得到两次故障暂态行波折反射的时间差,对比于小波方法,有无须选择基函数的优点,但在经验模态分解过程中容易出现模态混叠现象,会对最终测量结果造成误差。
针对上述问题,提出使用改进HHT对故障行波信号进行处理分析,HHT不用人为地选择基函数,并能对信号进行自适应分析,可以使信号在时频域内保持良好的特征;然后对经验模态分解中很容易产生的模态混叠现象加以改进,提出在进行经验模态分解的过程中加入辅助信号的方法来解决模态混叠现象,从而进一步提高电缆故障测距的精确性。
1 改进的HHT
HHT的内容由两个部分组成,第一部分是经验模态分解,第二部分是Hilbert谱分析。
1.1 经验模态分解(EMD)
频谱分析,是将信号分解成不同频率的成分。频率的实质是信号振荡剧烈的程度,而该程度通过信号的极值点信息来反映。EMD可以根据信号的极值点信息,将信号分解成多个本征模态函数。
1.1.1 本征模态函数(IMF)
IMF的特点是均值为0的纯振荡函数,如果一个函数f(x)在定义域内满足:(1)极值点与零点的数目相差不超过1;(2)上下包络函数的均值为0,则称函数f(x)为本征模态函数。而EMD方法就是将函数分解为若干本征模态函数及单调的残差,即:
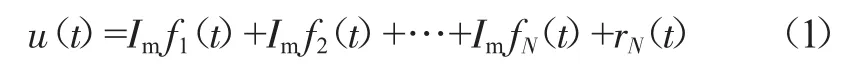
1.1.2 寻找本征模态函数IMF的方法
(1)针对给定的函数u(t),找出极大值点和极小值点。
(2)用曲线分别连接所有极大值点和极小值点,来得到极大值包络线emax(t)和极小值包络线emin(t)。
(3)对两条包络线进行平均,得到平均线,即:
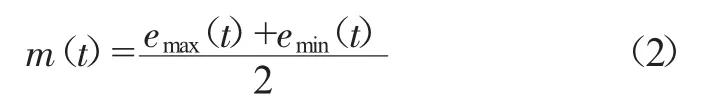
(4)减去平均值,得到新的函数h1(t)=u(t)-m(t)。
(5)用新函数h1(t)代替原先的u(t),然后重复以上步骤,得到hk(t)(k=2,3,…),当hk(t)满足本征模态函数的条件时停止,定义Imf1(t)=hk(t)。
1.1.3 EMD方法基本步骤
(1)针对给定的函数u1(t),找到第一个本征模态函数Imf1(t)。
(2)令uk=uk-1(t)-Imfk-1(t),继续寻找第k个本征模态函数(k=2,3,…),直到uk(t)为单调函数为止。
在实际使用中,hk(t)=0通常难以满足,可用如下条件代替:

满足式(3)即可认为hk(t)满足IMF条件,SD可设定在0.2~0.3[3]。
1.2 希尔伯特变换
信号经过经验模态分解后可以得到多个IMF,对这些IMF进行希尔伯特变换,就可以得到其瞬时频率。
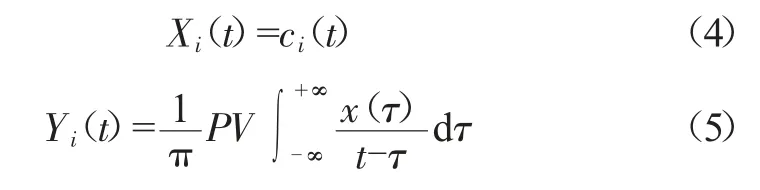
式中:P、V表示柯西主值积分。
经过希尔伯特变换之后,所有的本征模态分量即为:
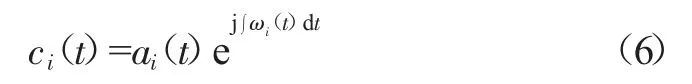
故原始信号可表示为:
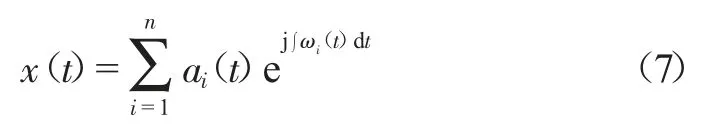
希尔伯特谱即为:
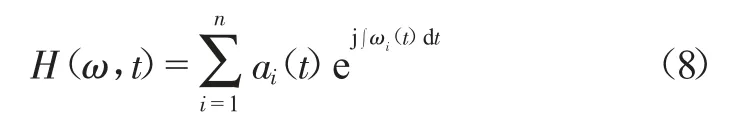
1.3 模态混叠消除
针对EMD在对信号进行分解的过程中容易产生模态混叠的现象,提出在进行EMD分解的时候加入辅助信号的方法,来克服此种问题。具体实施步骤如下:
(1)本征模态函数中是否存在模态混叠的判别式为:

(2)设置辅助信号ni(t),ni(t)为:
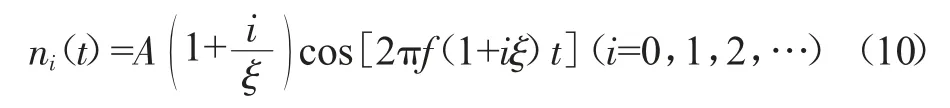
式中:A为IMF信号幅值均值的绝对值;ξ为原信号幅值均值与A值之比;f为IMF瞬时频率的均值。
(3)因为原信号中的非连续的成分与设置的辅助信号的特征相似,将辅助信号添加到原信号中可以将原信号中的不连续的部分转变为连续的,所以此时信号为:

(4)得到的新的本征模态函数若满足式(9),即模态混叠现象消除。若不满足式(9),则式(10)中的i加1,重新添加进原信号进行分解,重复步骤直到消除模态混叠现象。
2 电力电缆故障的行波测距
电力电缆发生故障会导致故障点处的阻抗不同,所产生的故障暂态行波在经过此点时会出现折反射现象,而故障暂态行波在线路中的传播速度是固定的,如果可以得到两次故障暂态行波折反射的时间差,就可以计算得到故障点所在的位置[4]。电缆故障行波分析图如图1所示。
打造编织限制权力的制度笼子并不是一件容易的事情,它是一项异常复杂且十分精细的工作。如何做到使所编织打造出的制度笼子能有效限制或规范权力?我们认为,在具体编织过程中,应当遵守以下几条基本原则。
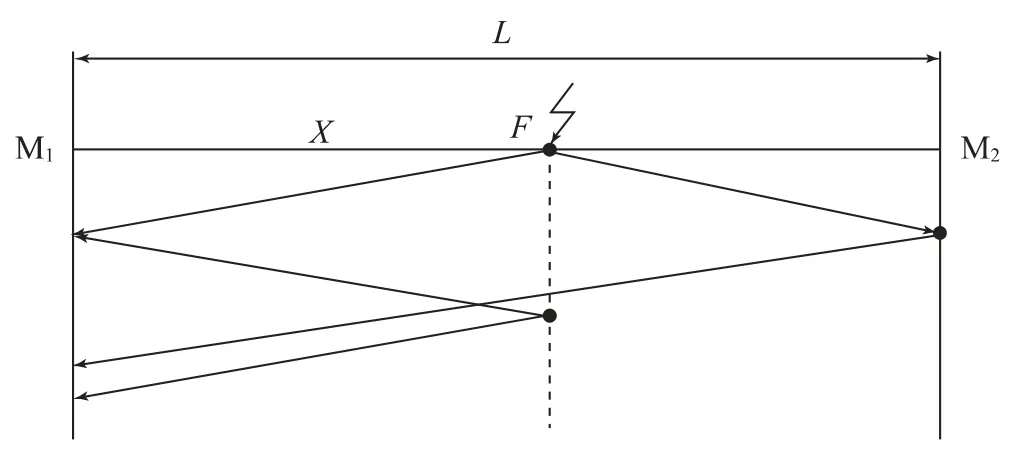
图1 电缆故障行波分析图
根据检测故障暂态行波的不同方式,可以将行波测距方法分为单端和双端检测方法[5]。双端检测方法会存在双端检测时间不同步、经济成本高等缺点,所以本文使用单端测距方法。然后采用改进HHT方法对采集到的故障暂态行波信号进行处理,从而得到故障暂态行波波头两次分别到达检测端的时间的差值。行波波速公式为:

式中:C、L分别表示线路的电容值和电感值。
单端行波测距公式如下,计算得出发生故障的点与检测端的距离[6]。

式中:x为检测端到故障发生点的距离;v为行波速度;Δt为故障暂态行波波头两次分别到达检测端的时间的差值。
3 电缆故障测距的Matlab仿真分析
运用Matlab仿真软件搭建电缆故障仿真模型,并对其进行分析,搭建的电缆故障仿真模型如图2所示。
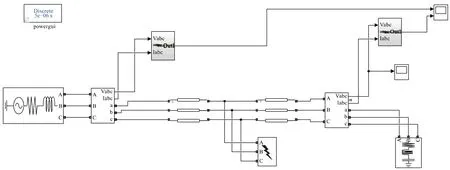
图2 电缆故障仿真模型
模型中的参数设置如下:系统中的电源电压为110 kV,频率为50 Hz,电缆总长度L为20 km。
电缆分布参数为:R1=0.012 73 Ω/km,L1=0.933 7×10-3H/km,C1=1.274×10-8F/km;R0=0.386 4 Ω/km,L0=4.126 4×10-3H/km,C0=7.751×10-9F/km[5]。仿真时间设置为0.1 s。
电缆故障为A相接地故障,故障开始的时间在0.010~0.011 s,采样频率为1 MHz。则由公式(12)可计算出行波波速为:

故障点设置在5 km处,A相接地故障电压波形如图3所示。对故障行波使用改进HHT进行分析处理的波形如图4所示。用改进EMD对信号进行分解得到的8个IMF如图5所示。对IMF1进行一阶微分处理,可得图6。
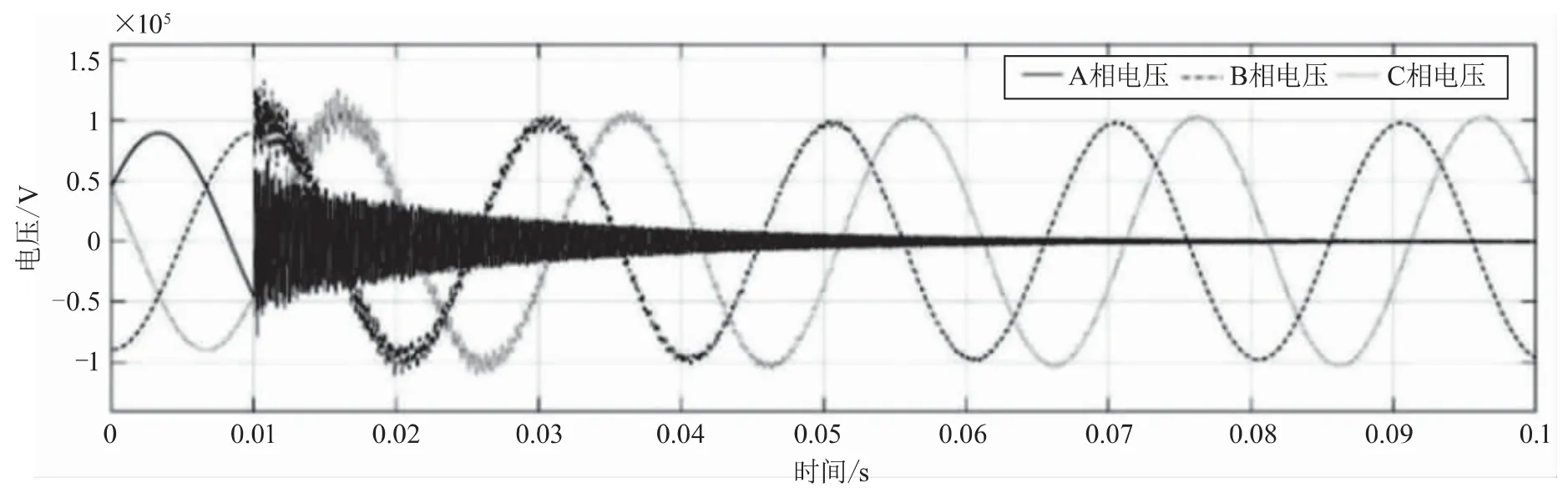
图3 A相接地故障电压波形图
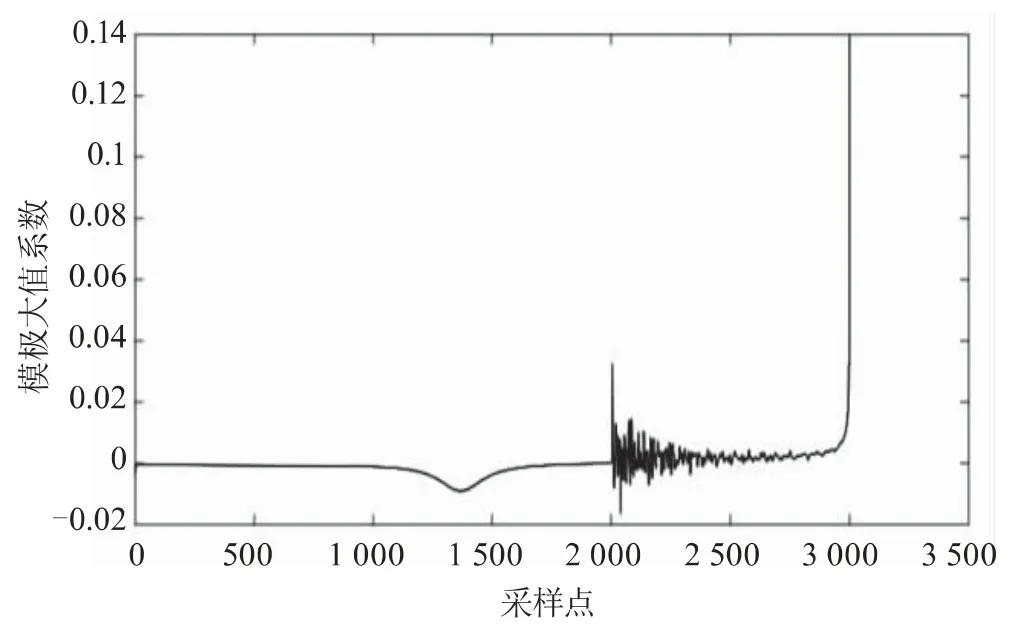
图4 故障行波的改进HHT分析图
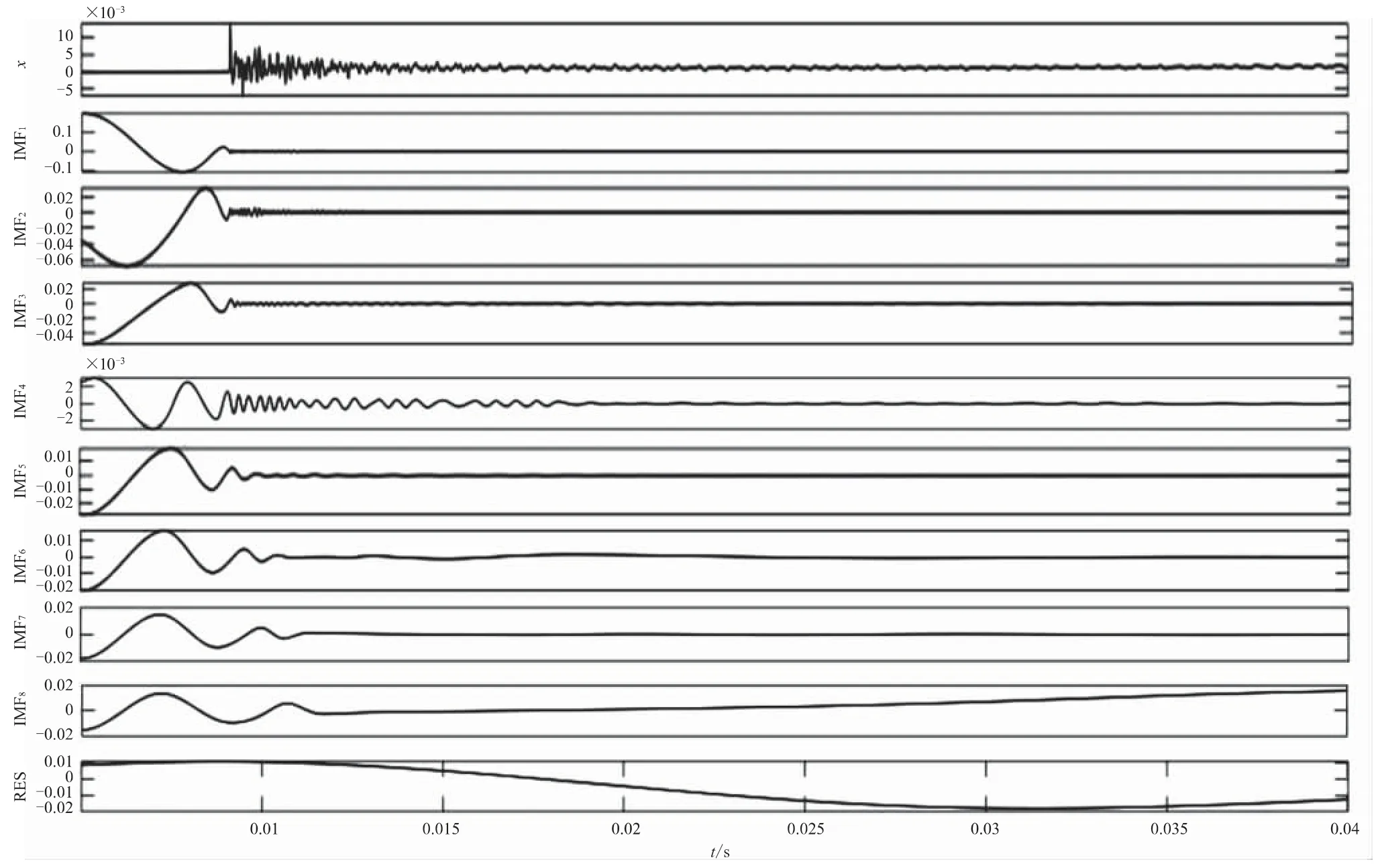
图5 IMF分量图
由改进HHT对信号的分析处理可以得到故障暂态行波波头两次分别到达检测端的时间差。由图6可知,故障暂态行波波头两次到达检测端的时间差值为57.2个采样点,即故障初始行波和故障反射行波到达检测端的时间间隔为57.2 μs。应用公式(13)计算得出发生故障的点与检测端的距离:
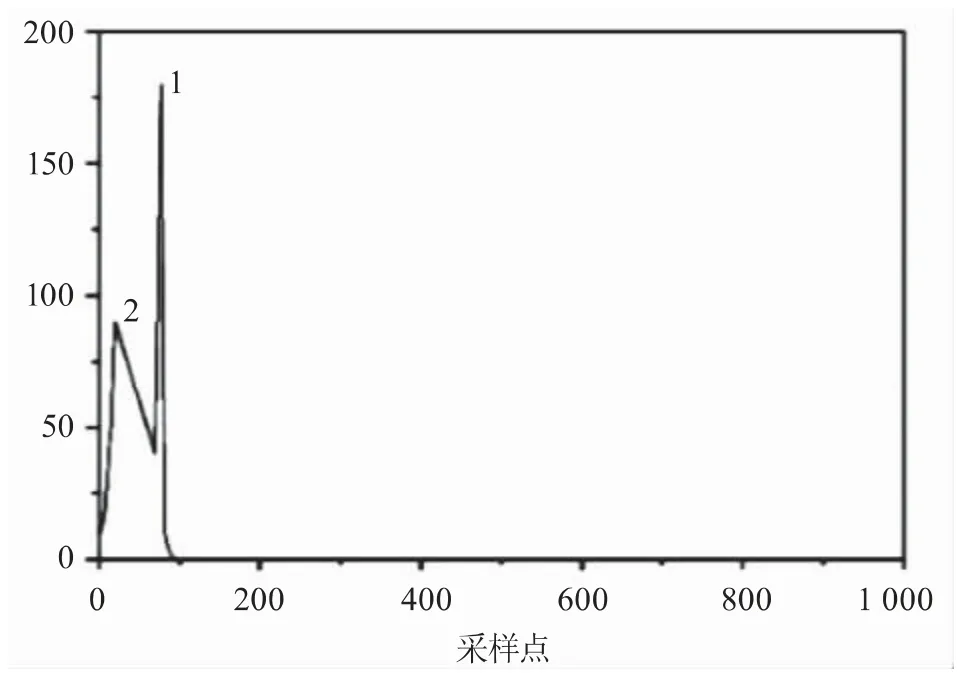
图6 IMF1的一阶微分图
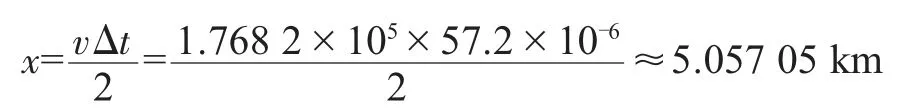
计算相对误差:
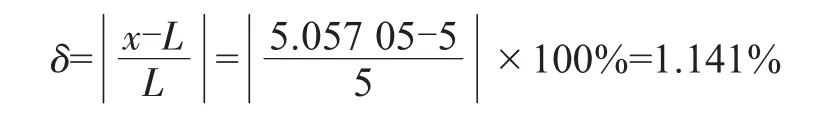
经过仿真分析与计算可知,改进HHT电缆故障测距方法的误差不到1.5%,相对误差较小,对比于传统电缆故障测距方法,提高了故障测距的精确度。
4 结语
通过分析EMD中存在的模态混叠现象,本文对HHT方法进行了改进,提出在进行EMD分解的过程中加入辅助信号的方法来消除模态混叠现象,并将改进HHT应用到电缆故障测距中。本文先用Matlab搭建电缆故障仿真模型,然后利用改进HHT对故障信号进行提取分解,通过奇异点的检测计算得到电缆故障点发生的位置。结果表明,改进HHT提高了电缆故障定位的精确度。
