移动边缘计算网络中的资源分配与定价①

吕晓东,邢焕来,宋富洪,王心汉

1(西南交通大学 信息科学与技术学院,成都 610031)

2(西南交通大学 计算机与人工智能学院,成都 610031)

1 引言

随着移动应用和物联网的快速发展,功率和计算资源有限的移动设备(MDs)不再满足资源密集型应用的严格要求,如低延迟、高可靠性、用户体验连续性的要求[1].在移动边缘计算(MEC)中,网络运营商和服务提供商进行合作,在网络边缘提供优秀的通信和计算资源,以增强MD 能力[2].

在MEC 中,计算资源的管理在提高资源利用率和优化系统资源效益方面起着至关重要的作用[3].由MEC服务器处理外部任务会消耗本地计算资源.因此,每个MD 根据某种资源定价机制支付一定的服务费,以激励边缘云提供足够的计算资源.

现有的定价机制,如基于拍卖的,依赖于中间机构的静态定价[4-6].拍卖双方都需要向中介提供的服务支付费用.总成本的增加使得双方都无法从资源交易中获得最佳的利益.同时,静态定价也不能适应MD 不断变化的资源需求.在这种情况下,MEC 服务器很难有效地利用其本地资源.因此,一个关键的问题是如何有效地将有限的MEC 资源分配给具有不同需求和偏好的相互竞争的MD.为此,我们将MEC 环境中的多资源分配和定价问题表述为一个包含一个领导者和多个跟随者的多阶段Stackelberg 博弈,其中所有MEC 服务器同时将它们的实时价格发送到一个聚合平台(AP).在第1 阶段,通过MEC 服务器公布的价格,AP 通过解决一个效用最大化问题来找到最优的资源分配解决方案.在第2 阶段,基于环境的反馈(即资源如何分配给MDs),我们利用多代理近端策略优化(MAPPO)算法[7]学习每个MEC 服务器的最优定价策略,这种策略不需要MEC 服务器获取其他MEC 服务器实现的定价策略就可以做出最优的决策.

我们的主要贡献如下: (1)我们通过构建一个Stackelberg 的领导者-跟随者博弈,充分考虑了AP 和MEC 服务器之间的互动以及服务器之间的竞争.纳什均衡给出了完全竞争的合理结果.(2)该算法基于MAPPO,这是一种具有集中式训练和分布式执行的深度强化学习算法,能够适应环境动力学和参数的不确定性.每个MEC 服务器作为一个智能体,不断地与环境交互,以生成一系列的培训经验.智能体既不需要事先了解MEC 资源的折扣成本,也不需要知道其他智能体所采取的行动.因此,信号传递的开销就大大减少了.(3)仿真结果表明,该算法可以为每个MEC 服务器学习一个优秀的策略,以确定其资源的单价.

2 相关工作

边缘系统的最优资源分配和定价已经引起了越来越多的研究关注.主要有两个研究方向: 定价导向因素和最优定价策略.

定价导向因素.Dong 等人[8]提出了一种云计算资源定价算法,分析历史资源使用情况并不断调整资源价格.但该算法只考虑了资源利用率,没有分析其他重要因素.Liu 等人[9]提出了一种基于价格的分布式算法,只强调了任务调度.Li 等人[10]提出了云计算的静态资源定价方案.定价操作简单,但难以满足终端设备的动态需求.他们没有考虑用户需求与资源价格之间的实时关系,因此不能根据用户需求动态调整资源价格.

最优定价策略.现有的最优定价策略大多是基于拍卖和博弈论的.Zhang 等人[11]研究了通过基于拍卖的算法对系统效益和多维资源的联合优化.解决方案是系统性能改进和单位效益的产物.然而,该算法以每一轮拍卖为优化目标,难以接近全局最优.因此,执行成本非常高.Dong 等人[12]采用了一种基于价格的双层Stackelberg 博弈来模拟一个由单个MEC 服务器和多个用户组成的MEC 系统.

3 系统模型

3.1 网络模型

MEC 系统模型由多个利益相关者组成: (1)希望出售免费资源的MEC 服务器; (2)希望购买资源以执行计算任务的MD; (3)AP 作为第三方代理,代表MD 从MEC 服务器购买资源.不失一般性,我们考虑一个通用的“多对多”场景,即每个MEC 都可以将资源出售给多个MD.同时,每个MD 可以购买多个MEC 服务器出售的资源.

我们考虑一个具有多个MD 和具有多种类型资源的多个MEC 服务器的MEC 系统.我们用U={1,2,···,U}和M={1,2,···,M}分别表示MD 和MEC 服务器的集合.R={1,2,···,R}表示资源种类的集合.我们有|U|=U,|M|=M,|R|=R.MEC 服务器和MD 之间的相互作用总结如下:

(1)MEC 服务器i∈M,希望出售空闲资源r∈R,于是向AP 告知它的可用资源数量Qi,r和其单位资源的期望价格pi,r.

(2)给定价格pi,r和可用资源数量Qi,r,MDj∈U决定从每个MEC 服务器购买的资源数量

(3)MDj使用所购买的资源来处理其计算任务.

3.2 多阶段Stackelberg 博弈

Stackelberg 领导者-跟随者博弈是一个策略游戏,其中领导者承诺一个策略,然后跟随者跟随[13].一般来说,游戏中的所有玩家都是自私的,因为他们每个人都考虑了他人的策略来最大化自己的利益.具体来说,考虑到跟随者可能采取的策略,领导者选择了一种最大化其利益的策略.基于观察领导者的策略,每个跟随者都采用了使其利益最大化的策略.然后,我们解释了跟随者之间的竞争.通过MAPPO 算法,得到了每个跟随者的最佳响应.在这个算法中,每个跟随者都与环境交互,并学习一种策略来优化其长期奖励,而不需要考虑他人采取的行动.Stackelberg 领导者-跟随者博弈的定义如下:

玩家: AP 和MEC 服务器都是游戏玩家.AP 是领导者,而所有的MEC 服务器都是跟随者.

策略: 对于MEC 服务器i∈M,他的策略是确定资源r∈R的单价; 对于AP,策略是确定MDj∈U从MEC服务器处购买的资源r的数量.

收益: MEC 服务器、MD 和AP 的收益函数分别由式(1)-式(3)给出.

令xi.j.r表示MDj∈U从MEC 服务器i∈M处购买的资源r∈R的数量.MEC 服务器i的收益计算如下:

其中,pi,r表示MEC 服务器i的资源r的单价,xi={xi,j,r}j∈U,r∈R,pi={pi,r}j∈U.

MDj的收益定义如下:

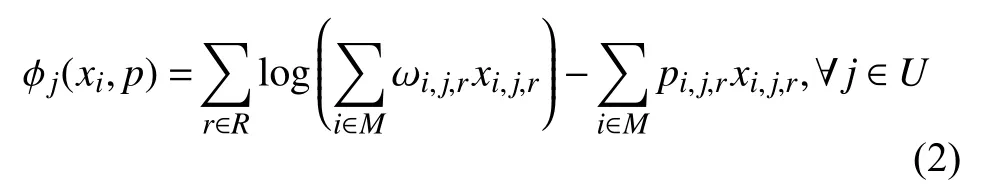
其中,xj={xi,j,r}i∈M,r∈R,p={pi,r}i∈M,j∈U,ωi,j,r是MEC 服务器i出售给MDj的资源r的质量.

AP 的收益是所有MEC 服务器和MD 收益的总和(即社会福利),定义如下:

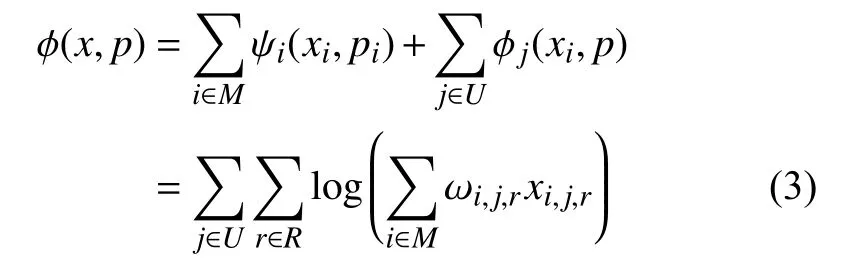
其中,x={xi,j,r}i∈M,j∈U,r∈R.

由于所有资源都有独立的预算,且彼此不受影响,因此我们可以将多资源分配和定价问题分解为多个单资源分配和定价子问题.因此,我们将优化问题分解为R个独立的子问题,每个子问题都与特定的资源类型相关联.与整体处理原始优化问题相比,该分解的主要优点是处理多个子问题显著降低了计算复杂度.与r∈R相关的子问题表示为:

其中,xi,r={xi,j,r}j∈U,xr={xi,j,r}i∈M,j∈U,pr={pi,r}i∈M.

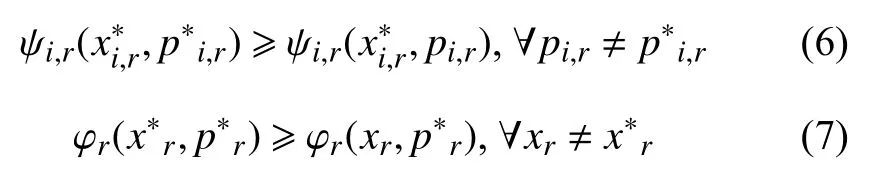
3.3 AP 社会福利优化

针对与资源r相关的子问题,给定所有MEC 服务器对资源r的单价(即pr),AP 的目标是最大化它的收益.

问题1:

其中,Qi,r是MEC 服务器i中资源r的可售卖数量,Bj,r是MDj购买资源r的预算.

定理1.问题1 的最优解如下:

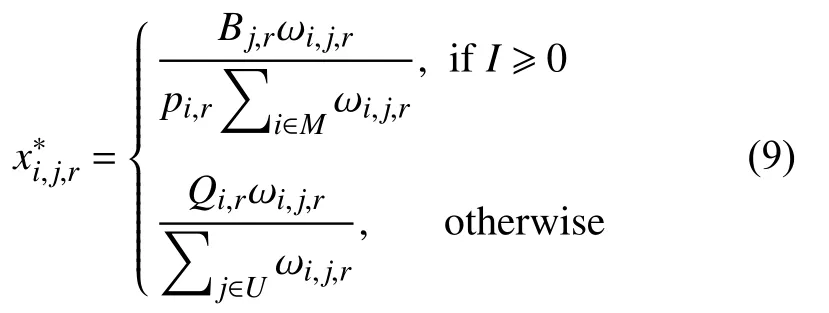
其中,

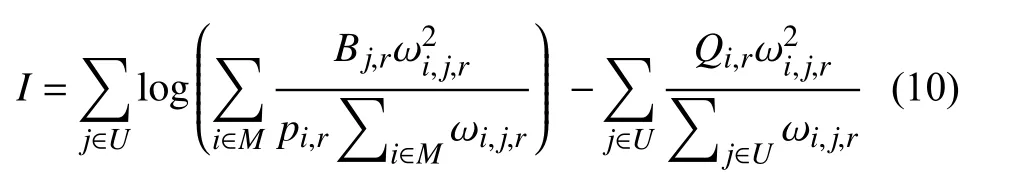
证明见附录A.

4 基于MAPPO 的AP 收益优化

本节将介绍每个MEC 服务器如何选择其对AP所采用的策略的最佳响应.

4.1 基于深度强化学习的方法

我们使用多智能体强化学习(multi-agent reinforcement learning,MARL)来解决多重单一资源分配和定价子问题.我们将每个子问题描述为一个马尔可夫决策过程(Markov decision process,MDP),以准确地反映资源分配和定价的决策过程.然后,我们将 MAPPO应用于这些子问题.由于其在全局优化方面的出色性能,MAPPO 可以在需要时快速为每个MEC 服务器获得接近最优的单一资源分配和定价策略.

对于资源r,给定来自环境的反馈(即资源r如何分配给MD),每个MEC 服务器需要确定资源r的单价以最大化它的收益.

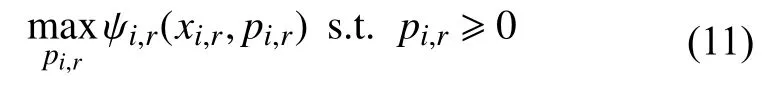
MDP 的元素如下所示,包括状态空间、动作空间和奖励函数.

状态空间: MEC 服务器i在时隙t时刻的状态空间表示为oti,包括对前面的L个时隙的观察,如式(12)所述:

全局状态: MAPPO 基于全局状态s而不是本地观察oi学习策略 πθ和值函数Vς(s).我们使用所有局部观测结果的连接来作为critic 网络的输入.

动作空间: 在时隙t,MEC 服务器i∈M观察前L个时隙的资源分配情况,决定在当前时隙的单价,即pti,r.

奖励函数: 奖励函数定义如下:

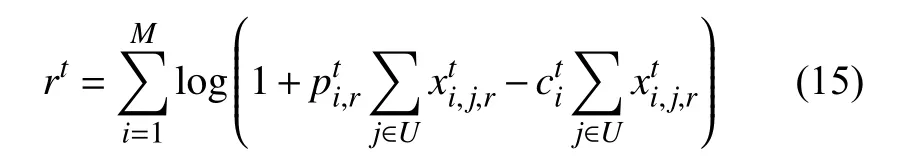
其中,cti是MEC 服务器i的折扣成本.log 函数确保当所获收益(即)不足以抵扣成本时,奖励是负的.

4.2 基于MAPPO 的资源分配和定价策略(RAPMAPPO)

MARL 算法可以分为两种框架: 集中式学习和分散式学习.集中式方法假设合作博弈,并通过学习单一策略直接扩展单智能体强化学习算法,以同时产生所有智能体的联合动作.在分散学习中,每个智能体都优化自己的独立奖励; 这些方法可以解决非零和博弈,但可能会受到非平稳转换的影响.最近的工作已经开发出两条研究路线来弥合这两个框架之间的差距: 集中培训和分散执行(centralized training and decentralized execution,CTDE)和值分解(value decomposition,VD).CTDE 通过采用actor-critic 结构并学习集中的critic 来减少方差,从而改进了分散的强化学习.代表性的CTDE方法是多智能体深度确定性策略梯度(multi-agent deep deterministic policy gradient,MADDPG)[14].VD 通常与集中式Q 学习相结合,将联合Q 函数表示为每个代理的局部Q 函数的函数[15],这已被视为许多MARL 基准测试的黄金标准.MAPPO 通过将单个近端策略优化算法(proximal policy optimization algorithms,PPO)[16]训练与全局值函数相结合,属于CTDE 类别.不同的是PPO 是一个on-policy 算法,MADDPG 是基于offpolicy 的算法,但是MAPPO 经过简单的超参数调整就能获得比较好的成绩.

在RAP-MAPPO 中,每个MEC 服务器都被视为一个智能体.每个智能体都有一个参数为θ的actor 网络和一个参数为ς的critic 网络.RAP-MAPPO 为每个智能体训练这两个神经网络.我们用Vς表示critic 网络,用 πθ表示actor 网络.我们使用统一的经验重放缓冲区来存储历史数据点以进行训练.RAP-MAPPO 是一种基于集中式训练和分布式执行的方法.在集中训练阶段,actor 网络只从自身获取观测信息,而critic 网络获取全局状态.在分布式执行阶段,每个代理只需要它的actor 网络(而不需要critic 网络).通过与环境的交互,每个代理都可以做出合适的资源分配和定价策略.

Actor 网络被训练用来最大化:

Critic 网络被训练用来最大化.

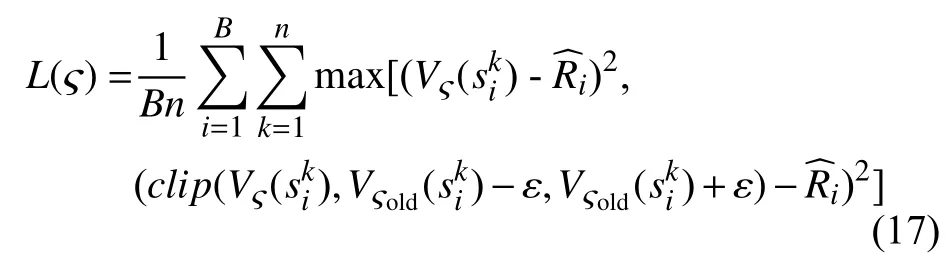
其中,是折扣奖励.RAP-MAPPO 的训练步骤见算法1.

算法1.RAP-MAPPO 的训练过程初始化: 初始化actor 网络和critic 网络的参数1: 设置学习率step≤stemmax α 2: while 3: 令 data buffer i=1 to batch_size D={}4: for do τ=[]5:6: for t=1 to T do pat=π(ota;θ),uta～pta,vta=V(sta;ς)7:utrt,ot+1,st+1 8: 计算动作 ,得到τ+=[st,ot,ut,rt,ot+1,st+1]9:images/BZ_105_405_1460_426_1491.pngA,images/BZ_105_430_1460_451_1491.pngRτ 10: 计算,将分成长度为L 的块11: for 1=1,2,…,T //L do D=D∪(τ[l:l+L,images/BZ_105_571_1561_592_1592.pngA[l:l+L],images/BZ_105_680_1561_701_1592.pngR[l:l+L]])12:13: 从D 中随机抽取K 个样本L(θ)θ L(ς)ς 14: 通过更新,更新

5 仿真结果

5.1 参数设置

我们考虑一个由多个MEC 服务器和多个MD 组成的MEC 系统.收益最大化问题取决于可用的资源和预算.为简单起见,我们设置ωi,j,r=1+0.1j+i/10.资源质量在整个实验过程中都是固定的.我们将长期奖励的折扣系数设置为零,因为自私的智能体的目标是最大化他们的即时收益.为了加快训练过程,我们对每个智能体都采用了一个相对较小的网络.Actor 网络和critic 网络都是由1 个输入层,3 个隐藏层和1 个输出层组成.这3 个隐藏层分别有128、64 和32 个神经元.此外,actor 网络和critic 网络都使用ReLU 作为所有隐藏层的激活函数,参与者网络采用tanh 函数激活输出层进行策略生成.其他模拟参数见表1.进行性能比较的算法如下:

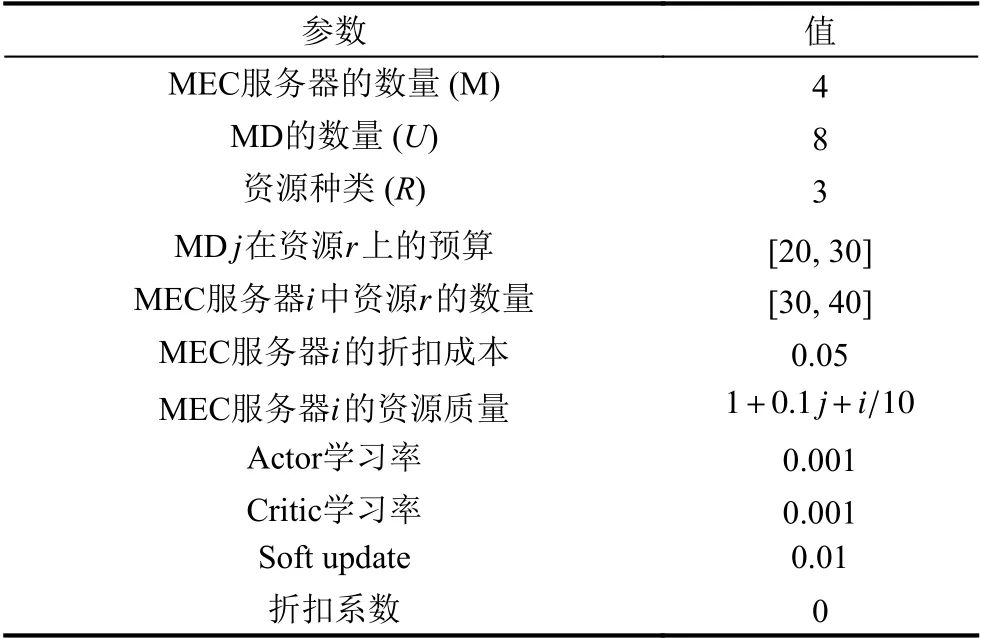
表1 仿真参数

质量比例最优定价(quality proportional optimal pricing,QPOP): 我们假设AP 对每个MEC 服务器提供的资源质量有一个先验的知识.单价设置与服务器的资源质量成正比,同时消耗确定的资源和货币预算(即I=0).I=0在实际系统中是不可能的,但由QPOP 找到的解决方案可以作为一个最优的基准.

随机: 单价在(0,5)区间内随机产生.

MADDPG: 每个MEC 服务器都被视为一个智能体,状态空间由前L个时隙的价格和资源分配组成,动作是资源的单价,奖励函数基于MEC 服务器的资源收入和成本设计.

5.2 收敛性

图1 为所提出的RAP-MAPPO 和MADDPG 在不同MEC 服务器数量下的收敛曲线.随着训练次数的增加,MEC 服务器的平均奖励逐渐上升,最终变为积极和稳定.我们首先研究了MEC 服务器的数量对收敛性的影响.随着MEC 服务器的增加,这两种算法都需要更多的时间来收敛.这是因为更多的服务器会导致更大的状态空间.这两种算法需要对状态空间进行更多的探索,才能获得可观的奖励.此外,MEC 服务器的平均奖励随着MEC 服务器的增加而降低.这是因为更多的服务器会在竞争期间降低价格,也就是说,每个服务器都希望出售其资源.然后,我们比较了两种算法在收敛性方面的性能.我们很容易观察到,与MADDPG 相比,RAP-MAPPO 具有收敛速度更快、平均奖励速度更高的特点.

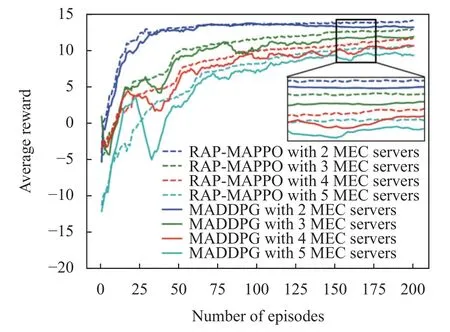
图1 不同算法的收敛性曲线

5.3 MEC 服务器和MDs 在Stackelberg 均衡下的收益

我们在两种场景下比较了这4 种算法.在第1 种场景下,Bj,r从5 到40 不等,Qi,r保持不变.在第2 种场景下,Qi,r均匀分布在[5,40]的范围内,Bj,r固定为20.为了说明预算约束的影响,我们在实验过程中固定了MD 的质量权重,并将M,U分别设置为4 和8.

在第1 种场景下,RAP-MAPPO 在没有对MEC 服务器提供的资源质量的先验知识的情况下,获得了接近最优的性能,如图2 所示.当MEC 服务器的资源不足时,MD 之间的激烈竞争导致了卖方市场.同时,RAPMAPPO 在社会福利方面优于MADDPG 和随机算法(见图3).这是因为随机定价不能充分利用MEC 服务器的资源,而RAP-MAPPO 则鼓励MEC 服务器动态调整其单价,以达到提高资源效率的目的.

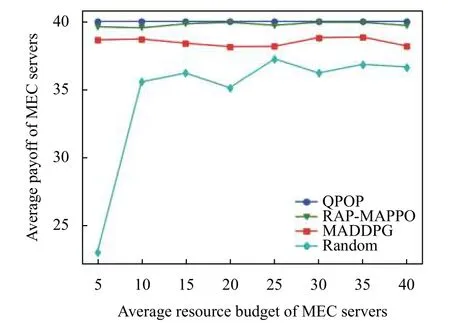
图2 不同MEC 资源数量下MEC 服务器收益

图3 不同MEC 资源数量下社会福利

在第2 种场景下,从图4 和图5 可以看出,在大多数情况下,RAP-MAPPO 在MD 收益和社会福利方面比MADDPG 和随机算法获得了更好的性能.随着MD 的平均货币预算的增长,MEC 服务器更有可能提高价格,以响应AP 的资源购买策略.因此,MD 需要降低他们的资源需求或支付更多的费用来鼓励MEC 服务器销售更多的资源,从而减少MD 的回报,即卖方市场.

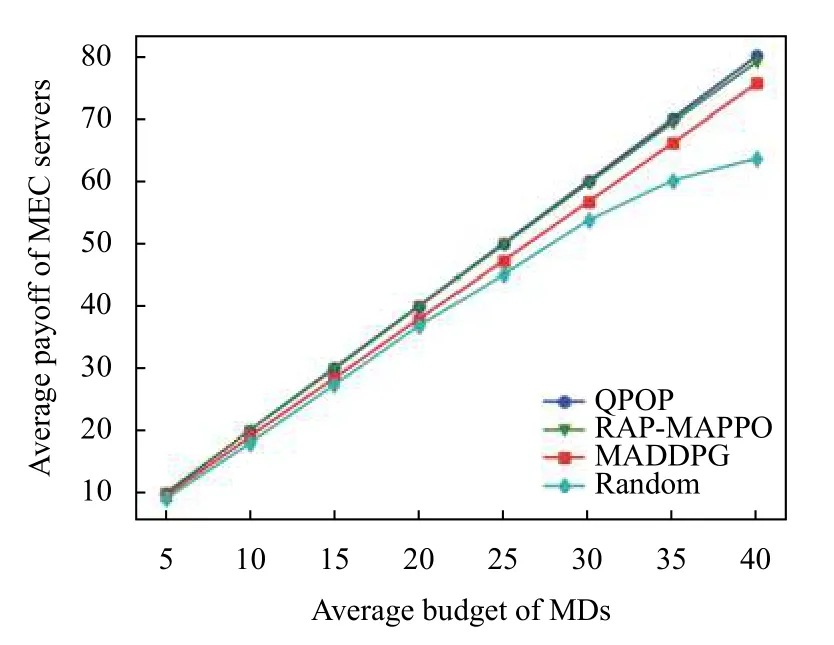
图4 不同MD 预算下MEC 服务器收益

图5 不同MD 预算下社会福利

综上所述,RAP-MAPPO 在MEC 服务器的收益和社会福利方面的表现优于MADDPG 和随机算法.它的性能与QPOP 类似.QPOP 需要知道MEC 服务器的质量权重信息和MEC 服务器之间的无条件合作,而我们的方法只是基于与环境相互作用的局部观察.

6 结论

本文研究了基于Stackelberg 博弈的资源分配和定价问题,其中AP 和MEC 服务器是领导者和追随者.这个问题被分解为多个可以单独解决的单一资源类型的子问题.我们采用MAPPO 来解决这个问题.对于任意的MEC 服务器,RAP-MAPPO 不需要知道其他MEC 服务器所采取的操作,这有助于减少信令开销.此外,RAP-MAPPO 可以通过一系列的状态-行动-奖励观察来指导竞争智能体实现收益最大化.仿真结果表明,在RAP-MAPPO 中,MD 和MEC 服务器在满足前者严格的货币预算约束的同时,学习了接近最优的回报.此外,RAP-MAPPO 在收益和社会福利方面都优于QPOP、随机和MADDPG.

附录A.定理1 的证明

问题1 对应的拉格朗日方程是:

KKT 条件如下:

消去 λi,可得:

因此,问题1 可以被分解为如下两个子问题.

子问题1:

子问题1 对应的拉格朗日形式的KKT 条件如下:

消去 λi,可得:

由式(25)可知:

另一方面,式(23)的可行解可推出:

因此可知:

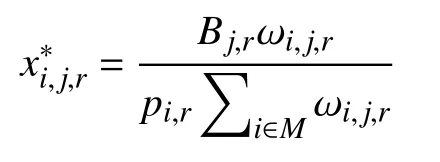
子问题2:

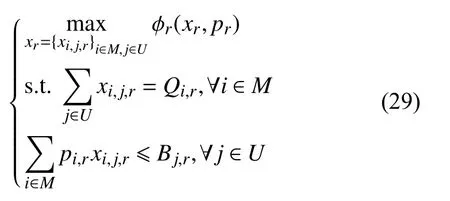
子问题2 对应的拉格朗日形式的KKT 条件如下:

消去 μj,可得:

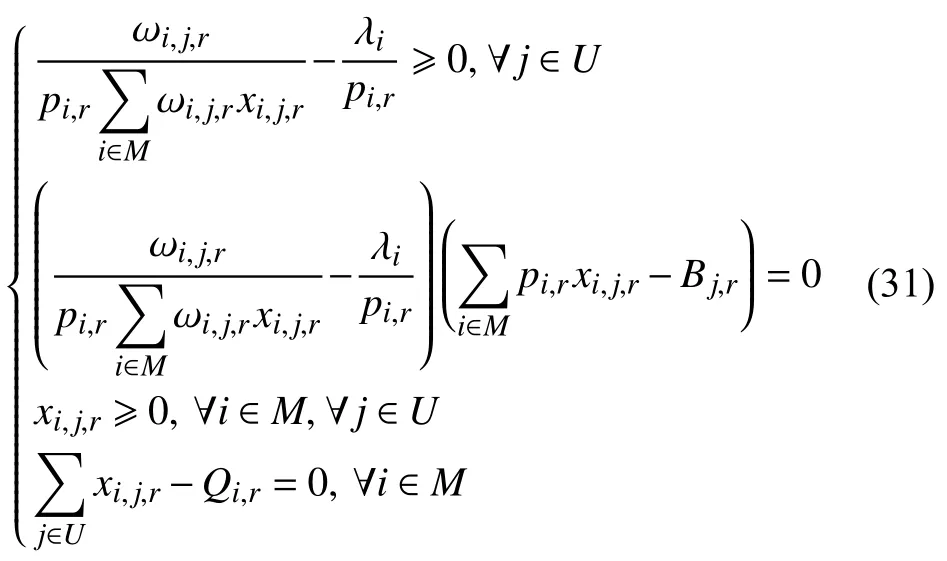
由式(30)可知:

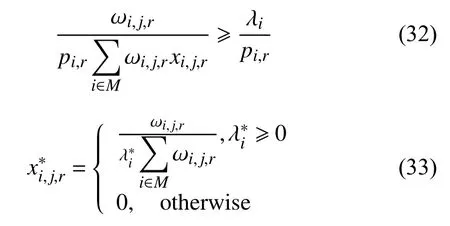
另一方面,式(29)的可行解可推出:

因此可得:

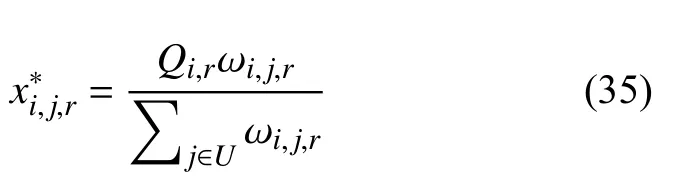
综上所述,问题1 的解如下: