数据赋能下上市公司财务舞弊识别及应用研究
2022-11-06邱晨炜罗苑玮
邱晨炜 罗苑玮



【摘 要】论文利用Python构建本福特审计模型分析样本单位数据,检验本福特定律识别审计风险的能力。通过分析样本单位财务报表数据中首位数字与本福特定律之间的关联程度,以验证本福特定律在审计过程中识别目标单位财务舞弊行为的可行性。
【关键词】大数据审计;本福特定律;Python
【中图分类号】F832.5;F275;F239.4 【文献标志码】A 【文章编号】1673-1069(2022)08-0152-04
1 引言
信息技术的不断迭代及数字赋能时代的到来为现代化审计工作带来了巨大的机遇和挑战。机遇是若能适应数财融合背景下审计实践的迭代并且从中探索出一条能高效识别舞弊风险的道路,将加速审计理论和审计实践的融合,促进审计质量的提升。而挑战是随着上市公司的季报、中报、年报和说明,从原先的几十页到现在的上百页,各种数据信息呈几何式陡增。在纷繁复杂的大数据面前,如何高效地识别出被审计单位所提供的资料中的问题,这是摆在所以审计人眼下一个急需被处理的课题。
2 本福特定律的含义及检验方法
2.1 本福特定律的含义
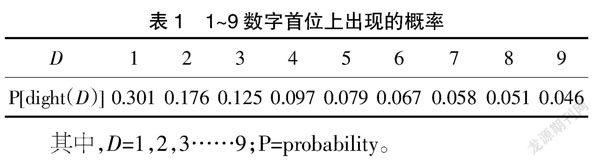
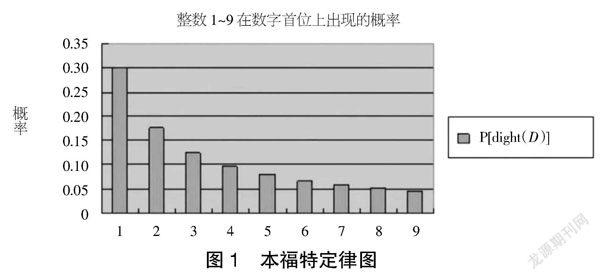
本福特定律命名来源于20世纪的英国科学家本福特,他通过分析了20 229组自然形成的数字后得出:在一组自然形成的数字中,以1为首位出现的概率大于以2为首位出现的概率,以此类推,以9为首位出现的概率最低。并且本福特进一步测算出了其出现的概率,如表1、图1所示。
其中,D=1,2,3……9;P=probability。
2.2 本福特定律的检验方法
本文主要通过构建模型检测数据首位数字的分布频率是否符合本福特定律,最后采用卡方拟合优度进行检验。
2.2.1 提出假设
本文针对卡方检验,提出以下两个假设。
原假设M1:样本数据首位数(1~9)的频率分布遵循本福特定律。
备择假设M2:样本数据首位数(1~9)的频率分布不遵循本福特定律。
2.2.2 卡方拟合优度检验
卡方统计量为:
其中,Ai是样本数据中首位出现数字的实际分布频率,即实际观测值;Ti是本福特定律下首位出现数字的理论分布频率,即理论推断值。若卡方统计量的检验结果小于临界值时,接受原假设M1,说明统计数据首位数字的频率分布符合本福特定律。若大于临界值时,接受备择假设M2,说明统计数据首位数字的频率分布不符合本福特定律。
3 本福特定律验证的案例引入及模型构建
上市公司常见的财务舞弊手段包括收入造假、费用造假、高估资产、伪造交易的真实性等,在进行数据造假的过程中便使得数据首位数的分布概率与本福特定律产生偏离。因此,本文主要选取了10家样本公司近15年的财务数据进行本福特定律检验。目的是观测各财务数据与本福特定律是否显著偏离,比较偏离程度并讨论其深层次的含义。
3.1 样本选择与数据来源
如表2所示,分别选取因财务造假而被公开处罚或在网上留下财务舞弊记录的5家上市公司(记为“负向公司”)和5家未被处罚过的公司(记为“正向公司”)作为本文的研究样本。将10家公司所公布的经审计后的资产负债表、利润表数据中部分不具备随机产生和杂乱无章特点的数据删除后,作为本案例分析基礎。最终得到共计1 167列案例研究样本。
3.2 模型构建
3.2.1 数据预处理
数据清洗即去除信息中的重复信息和错误信息,这些数据会影响后续的分析,数据清洗的过程对数据分析十分有必要。
样本公司数据取自其公布的资产负债表和利润表2008年3月至2022年6月的季报、中报和年报,在剔除了人为因素影响的会计信息和空缺信息后中国平安的有效数据共计4 400个、招商银行的有效数据共计3 125个、五粮液的有效数据共计3 070个、隆基股份的有效数据共计3 124个、万科A的有效数据共计3 450个、*SR国药的有效数据共计2 506个、金亚科技的有效数据共计2 319个、圣莱达的有效数据共计2 399个、欣泰电气的有效数据共计1 729个、太化股份的有效数据共计2 707个。
3.2.2 数据采集
数据分析的起始性操作是对数据进行采集。没有数据,就无法分析。本文主要运用Python语言爬取预先处理好的目标企业财务数据的方式实现数据采集。
本文算法主要通过调用Os和Re模块改变当前工作目录到存放数据所在的文件夹路径并返回指定文件夹包含的数据文件,在抓取了档案的位置后,通过Pandas和Numpy模块对本文所需要的详细数据进行运算和解析,最终数据会保存在指定的文件中以备后续运用Stats模块进行卡方检验。关键代码如下:
import os,re
import pandas as pd
from scipy import stats
import numpy as np
np.seterr(divide='ignore', invalid='ignore')
pd.set_option('max_rows', None)
3.2.3 数据清洗
数据清洗即去除信息中的重复信息和错误信息,这些数据会影响后续的分析,数据清洗的过程对数据分析十分有必要。由于企业可能存在亏损情况,则利润表中的数据会以负数形式呈现,而因负值数据和正值数据的开头数字不好同比,本文将负值数据取绝对值后再进行后续操作。主要包括以下步骤:去除原数据中数字间的逗号;将原数据中的负数转为正数。除此之外,还需要剔除过小值。关键代码如下:
def Get_First_num(input):
output = 0
try:
if input != 'nan' and len(input) > 0:
input = float(input.replace(',', ''))
input = abs(input)
if input > 20 or input <-20:
output = int(str(input)[0])
else:
pass
3.2.4 统计首位字母出现次数
在对数据进行清理后,定义计数规则,对原数据中出现的0~9的次数进行统计,统计出各目标公司中各数字出现的概率。关键代码如下:
def Count_num(num_count, input):
output = Get_First_num(input)
if output == 1:
num_count[0] += 1
elif output == 2:
num_count[1] += 1
elif output == 3:
num_count[2] += 1
elif output == 4:
num_count[3] += 1
elif output == 5:
num_count[4] += 1
elif output == 6:
num_count[5] += 1
elif output == 7:
num_count[6] += 1
elif output == 8:
num_count[7] += 1
elif output == 9:
num_count[8] += 1
3.2.5 计算数字分布
计算依照本福特定律,财务报表中各个首字母的期望次数并进行卡方检验。关键代码如下:
def Get_expected(sum_sheet):
expected_benford =[]
for i in sum_sheet:
benford = [0.301, 0.1761, 0.1249, 0.0969, 0.0792, 0.0669 ,0.058, 0.0512, 0.0458 ]
list1 =[round( x *i ,2) for x in benford]
expected_benford.append(list1)
return expected_benford
3.2.6 讀入代码进行技术并输出结果
读入代码进行计算后,将最终的计算得出的结果存在dataframe并输出结果。关键代码如下:
for root, dirs, files in os.walk(path):
for file in files:
profitsheet_num = compute_num(path, file)
actual_num = profitsheet_num
for i in range(0, len(profitsheet_num)):
sum_sheet.append(sum(profitsheet_num[i]))
expected_benford = Get_expected(sum_sheet)
finally_answer = Chi_test(len(profitsheet_num), actual_num, expected_benford, P)
sum_sheet.clear()
actual_num.clear()
expected_benford.clear()
print(file)
company.append(re.findall('(.*?)\.', file)[0])
cannot_reject.append(finally_answer.count(0))
can_reject.append(finally_answer.count(1))
dict = {"B_cannot_reject": cannot_reject,
"can_reject": can_reject,
"A_company": company,
}
df_final = pd.DataFrame(dict)
df_final.to_excel('{}\{}.xlsx'.format(path1,pan))
4 检验结果及分析
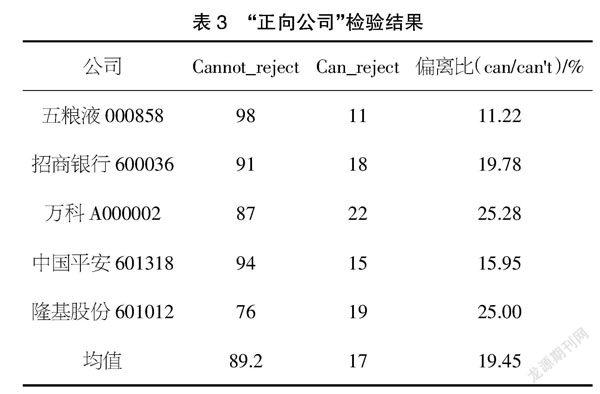
检验结果如表3和表4所示,我们可以清晰地看出“负向公司”的偏离比明显高于“正向公司”,这在一定程度上说明了本福特定律对未发现财务造假公司和已存在造假行为公司有所区分,尤其是在已存在舞弊行为公司身上出现大幅度偏离本福特定律分布的现象。同时,这也意味着通过本福特定律在审计过程中对审计对象进行初步筛选是可靠的。
通过运用此定律,审计人员对目标企业进行审计时,可以先将所分析的数据划分为“一般关注”“重点关注”和“异常”3类,在对比目标数据值与理论推测值符合程度的好坏后,确定哪张报表、哪项数据对审计分析影响不大,哪张报表、哪项数据存在异常需要被重点关注,以此来提升审计监督的效率和有的放矢地控制审计监督的成本。
5 政策建议
为提升审计人员的审计效率,本文提出以下的建议。
5.1 在开展审计工作前,审计人员可预先进行抽样检验
通过运用本福特模型,审计人员在开展审计工作前,可以测度该企业的财务数据是否与本福特定律的偏离程度相一致,若是偏离程度过大,则细查是哪张报表、哪个科目存在数据失真失实的问题,再以此为突破口,然后究根溯源,提升审计取样的针对性。
5.2 企业完善会计内部控制制度
在聘请外部机构进驻企业进行审计前,企业的内审部门应该预先进行自检、自查、自监,对企业自身财务报表的准确性和真实性负责。通过完善企业内部控制制度,对企业的下属控股的子公司进行统一管理和统一审查,不给财务造假的人有可乘之机。除此之外,企业还应提升自身的电子信息化程度,将高新技术与内部审计人员结合,通过外部购买或内部开发的方式,建立一套适合自身企业的电子信息化的财务检查系统,运用计算机技术来甄别财务数据、防控审计风险,在发现疑似人为修改和伪造的虚假信息时发出报警信息,为内审部门的科学审计提供技术保障。
5.3 政府强化对企业财务的监督,加大处罚力度
企業进行财务舞弊的原因:一是在于舞弊成本过低,在巨大收益面前,企业高管往往会忽视财务造假所带来的处罚风险;二是在于企业高管存在侥幸心理,认为只要造假技术水平足够高,那么财务舞弊很难被发现,因此虽然政府加大了对各行各业的监管力度,但企业仍会顶风作案。
为此,各级政府除了需要完善现有企业财务监督和管理的制度外,还需加大对造假企业的惩罚力度,这种惩罚需要经济罚款、行政制裁和媒体曝光等多领域、全方位、立体化并行,实现处罚上的一体化,以此来扶正各行各业的经营风气。
【参考文献】
【1】王虓,张锐.本福特定律在审计抽样中的应用研究[J].天然气技术,2009(04):66-67.
【2】罗玉波.本福特定律在财务审计中的应用研究[J].会计之友,2010(09):76-78.
【3】刘云霞,吴曦明,曾五一.关于综合运用Benford法则和面板模型检测统计数据质量的研究[J].统计研究,2012,29(11):74-78.
【4】罗玉波.大数据环境下本福特定律的审计应用研究[J].中国内部审计,2018(01):24-30.
【5】缑小平,杨金忠.本福特定律在部门决算数据质量评估中的应用研究[J].公共财政研究,2019(02):26-42.
【6】 彭仕宸.上市公司财务造假动因及手段研究[J].技术与市场,2021(04):138-141.
【7】吴冬惠.基于本福特定律的财政大数据审计验证方法[J].审计与理财,2021(07):10-11.
【8】丁文浩,朱齐亮.基于Python的招聘数据爬取与分析[J].网络安全技术与应用,2022(01):43-45.
【作者简介】邱晨炜(1994-),男,广西南宁人,壮族,硕士研究生在读,从事会计信息系统和大数据分析研究。
