六自由度欠驱动AUV系统建模技术研究

杜吉庆 周 丹

(1.苏州中寰园林设计有限公司 江苏苏州 215000; 2.扬州市兴创环境科技有限公司 江苏扬州 225000)

0 引言

当前随着海洋的开发越来越深入，AUV(Autonomous Underwater Vehicle)的应用越来越广泛[1]，例如海洋资源探测、军事应用、救灾救援、地图绘制等，各种应用的要求也随之提高，而精确的AUV系统运动模型是实现各种应用的前提。

AUV系统的非线性和工作环境未知性使得建模困难，为了快速获得AUV系统的控制模型，参数辨识、模型简化和数值建模是建模研究的热点，AUV系统的高非线性和不确定性，称为未建模动力学[2]。计算流体动力学(CFD)被用来对形状不规则系统的模型进行详细分析，Timothy在建模水动力方面做出很大贡献[3,4]。本文在上述文献基础上，描述建模细节，并对参数意义进行说明，所建立模型可以直接根据结构参数进行修改并编程应用。

1 AUV系统运动学模型

以美国Hydroid所研制的一种欠驱动鱼雷型AUV系统为对象进行建模[3]，如图1所示，AUV系统的建模包括运动学模型和动力学模型两个部分，其中运动学模型对物体运动过程中的位置、速度和加速度之间的关系进行描述，而动力学模型则是用来描述加速过程中的动力变化。

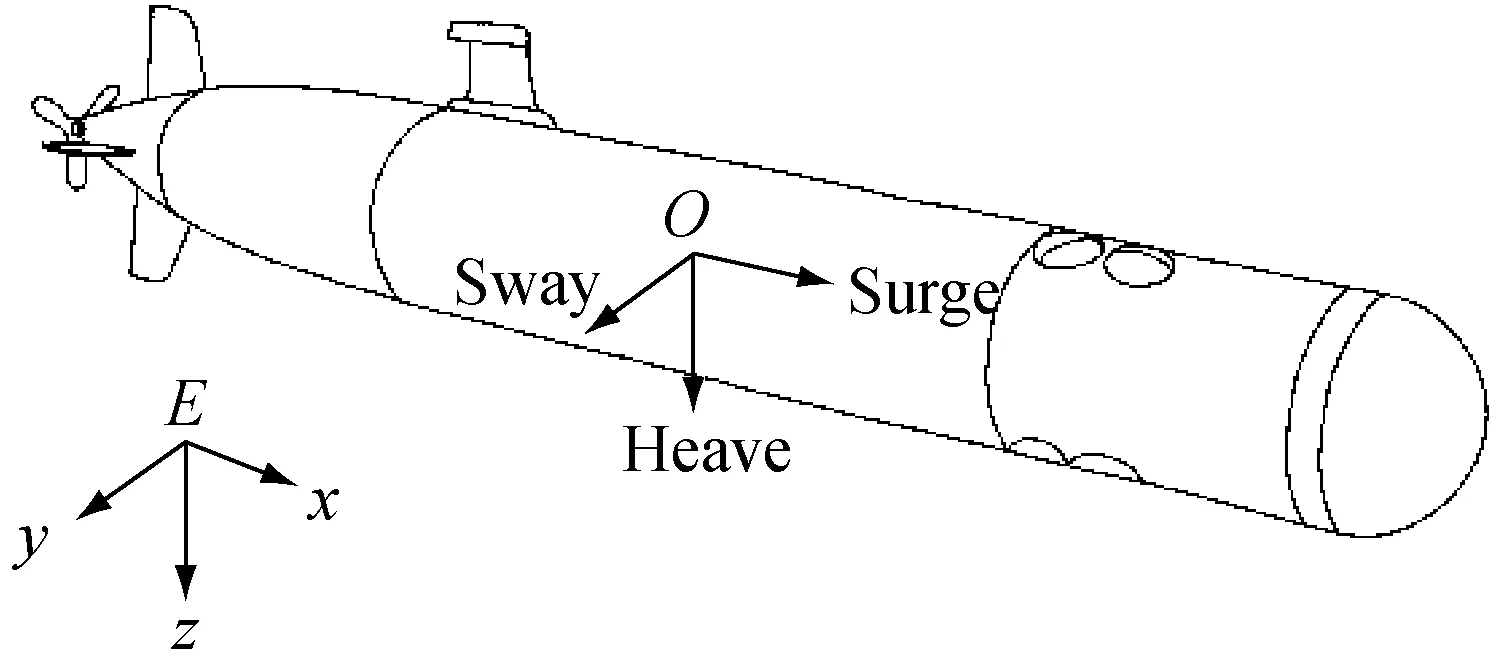
图1 AUV系统结构示意图

本文的AUV数学模型源于Fossen的海洋航行器[4]，相关模型的定义则可以参考SNAME(society of naval architects and marine engineers，1950)[5]，此规范定义了两套坐标系，分别是体坐标系和大地坐标系，各种定义和符号如表1所示。

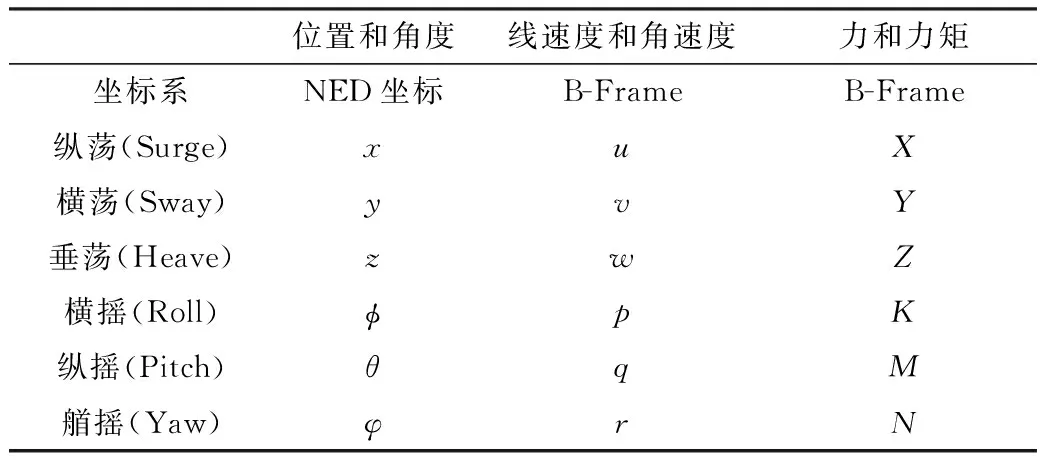
表1 SNAME坐标定义

运动学模型主要解释AUV系统运动变量的几何关系，不考虑引起系统运动及变化的力和力矩。体坐标系和大地坐标系变量之间可以进行相应的转换。

AUV系统的参数包括位置向量η、速度向量ν和推力向量τ，各个变量的定义分别如下所示：

η=[x,y,z,φ,θ,ψ]T

(1)

v=[u,v,w,p,q,r]T

(2)

τ=[X,Y,Z,K,M,N]T

(3)

其中位置向量η对应大地坐标系，原点的绝对位置(x,y,z)和转角姿态(φ,θ,Ψ)[6]。体坐标系是定义在AUV的浮心上的坐标系，速度向量ν表示AUV沿着体坐标系的三个轴的线速度(u,v,w)和三个绕轴的角速度(p,q,r)。而推力向量τ(X,Y,Z,K,M,N)表示AUV系统所受的外部推力和力矩在体坐标系下的矢量表示。将上述两个坐标系下的变量进行坐标变化，变换矩阵J(η)∈R6*6，J(η)是转换矩阵，且是可逆矩阵。

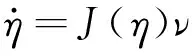
(4)

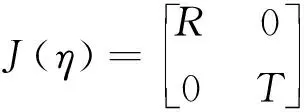
(5)

其中欧拉角η=[φ,θ,ψ]T分别是AUV系统的横摇、纵摇、艏摇角度，R(η)是线速度转换矩阵，是体坐标系到大地坐标系的转换矩阵，T(η)是角速度转换矩阵，是体坐标系到大地坐标系的转换矩阵，同理，如果是从地面坐标系到体坐标系转换[6]，采用逆矩阵的形式。其中R(η)和T(η)分别定义如下，

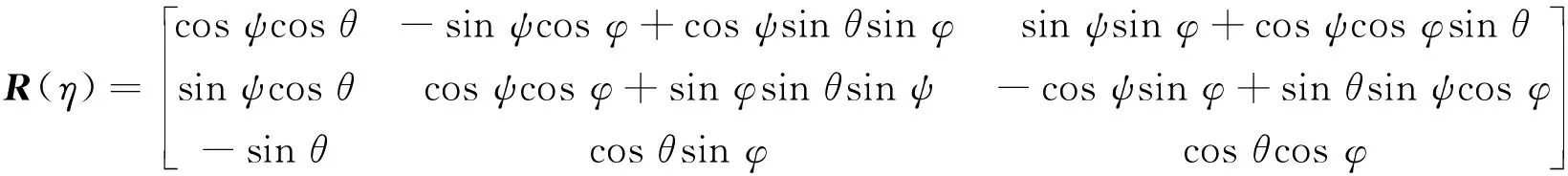
(6)

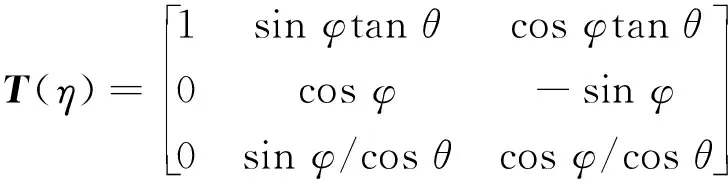
(7)

当θ=±90° 时，T(η)是不存在的，因此，AUV系统的角度存在一定的范围，横滚角φ：-π<φ≤π；纵倾角θ：-π/2<θ<π/2。

实际系统在应用过程中，为了设备安全，姿态角具有一定的约束条件。本系统约束条件为：横滚角φ：-π/4<φ<π/4 ；纵倾角θ：-π/4<θ<π/4。

2 AUV系统动力学模型

AUV系统的动力学部分可以根据线性定理进行叠加，AUV系统的水动力和航行动力包括刚体运动分析和水动力分析两部分，两者可以叠加。动力方程包括动量和动量矩方程，动量方程也就是线性动量，与直线运动有关系，p=mv，而动量矩方程式用角动量表示，与旋转有关系，L=mv×r。

2.1 AUV系统刚体运动分析

理想情况下，AUV系统可以视作无水环境中的理想刚体。刚体运动包括平移运动和旋转运动，不考虑水动力，刚体运动紧凑表达式为:

(8)

其中各个变量的定义如下：

MRB：AUV的刚体质量和转动惯量生成的矩阵；

CRB：科里奥利(Coriolis)力和力矩的矩阵；

τenv：外部环境作用力和力矩，包括风、浪、洋流等；

τpro：推进器的力和力矩。

2.1.1 惯性矩阵MRB

(9)

本系统为对称的AUV系统，质量矩阵分布在矩阵的对角线上[8]。所以式(9)中M11是mI3×3。此时MRB可以写为如下形式：

(10)

惯性矩阵MRB的右下角I0是AUV相对于体坐标系(B-frame)原点的转动惯量矩阵，惯性张量矩阵(Inertia tensor vector)是对称正定矩阵，I0的所有元素是AUV围绕轴旋转的转动惯量。质心的转动惯量：

(11)

此时标准MRB公式如下：

MRB=

(12)

斜对称矩阵S(λ)=-sT(λ) ：

(13)

λ=[λ1,λ2,λ3]T

(14)

细节计算：

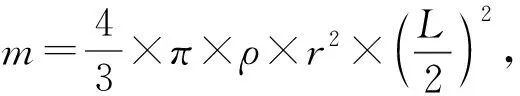
其中Ix、Iy、Iz都是相当于X0/Y0/Z0轴的转动惯量。当体坐标系的主轴{Xb,Yb,Zb}和惯性坐标主轴重合时，此时，可以将I0简写为Ig：

Ig=diag {Ix,Iy,Iz}

(15)

(16)

2.1.2 科里奥利力CRB(v)

CRB(v)是科里奥利力的斜对称矩阵。且与MRB和速度v有关，MSS(marine system simulation)[6]提供了计算方法。

定义如下所示：

CRB(v)=

(17)

CRB(v)=

(18)

上述公式展开为如下形式：

(19)

对于速度比较小的系统，可近似认为CRB(v)=0。从上式可见，当各个速度都是0，总体为0。

2.2 AUV系统水动力分析

AUV的水动力主要包括附加质量力、阻尼力和回复力，AUV水动力作用效果可以按照线性叠加在刚体运动基础上[9]，由Fossen的模型[1]，水动力作用表达式为τhydro：

(20)

其中：

MA：附加质量矩阵；

CA：科里奥利力和力矩的附加质量部分矩阵；

D：阻尼矩阵；

g(η)：回复力矩阵；

下面分别对上述各种水动力组成部分进行说明和分析。

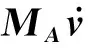
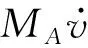
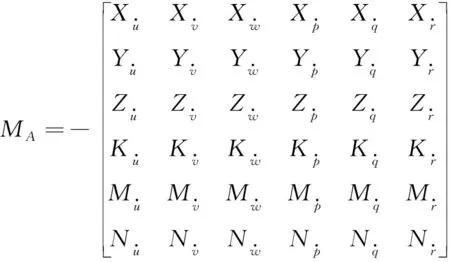
(21)

式(21)MA中各变量为水动力参数，与AUV系统的形状参数L相关，尤其是MA的对角线的参数与L3成正比，其他参数与L4成正比，且与水的密度ρ成正比。

附加质量力可以简写为如下形式：

(22)

理想情况下，MA是正定矩阵，且对角线元素大部分情况下是正数，极少情况下是负数[10]。实际情况下，AUV系统低速运行时，非对角线的元素小于对角线上元素，特别是对于水下具有对称性的AUV系统，非对角元素基本可以忽略不计，式(22)可以简化为对角矩阵：

(23)

细节计算：

附加质量力计算过程参数:

(24)

(25)

(26)

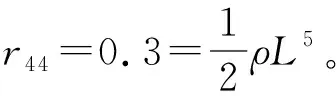
2.2.2 附加质量引起的科氏力CA(ν)ν

附加质量引起的科氏力CA(υ)υ与MA和速度υ有关。

(27)

实际科氏力写成速度ν和MA的形式：

CA(v)=

(28)

2.2.3 回复力g(η)

AUV系统在垂直面上受到作用于重心的垂直向下的重力W和作用于浮心的垂直向上的浮力B，水面航行器平衡条件是W=B，且作用于同一条铅垂线。对于水下AUV系统而言，通常被设计成接近零浮力的临界状态，即重力W略小于浮力B。回复力决定了系统的初稳性，也就是AUV系统受到外来作用力脱离平衡状态时，重力和浮力共同作用使系统恢复平衡的能力，浮心高于重心可以产生恢复平衡的扭矩。

W=mg

(29)

B=ρg∇

(30)

AUV系统在零浮力状态时，回复力可以用如下公式表示：

(31)

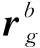
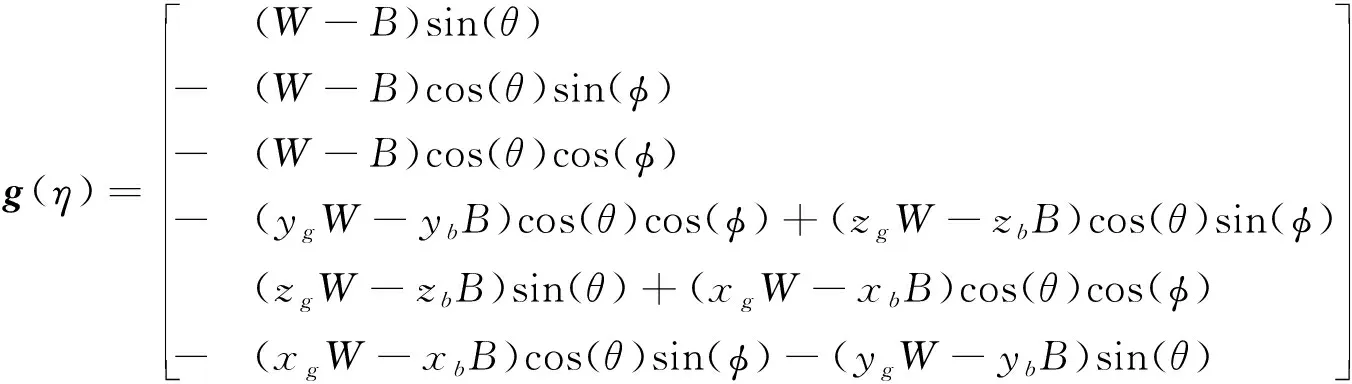
(32)

当选择运动坐标系的原点定义在重心时，rg=03×1，且当W=B时：

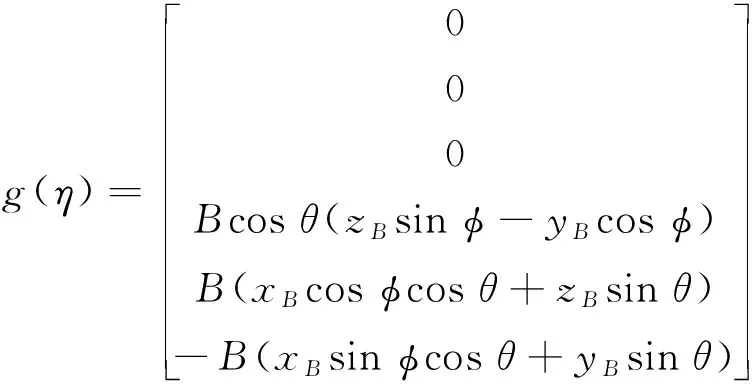
(33)

如果运动坐标系的原点定义在重心时，rg=03×1，但是W≠B。

2.2.4 流体阻尼力D(|v|)

阻尼力按照构成的性质可以被分为4种：

1)势流阻尼:DP(potential damping), 由辐射引起的阻尼， 基本可以忽略不计。

2)表面摩擦阻尼:DS(skin friction)。

3)兴波阻尼：DW (wave drift damping)，AUV系统在波浪作用下的阻尼，对AUV系统产生阻力作用。 由于AUV系统大部分时间工作在水下，因此，此部分可以忽略不计。

4)旋涡脱落阻尼：DM(vortex shedding damping)，是AUV系统在粘性流体中运行的耗散能量。

此处按照文献[6]把D(|v|)划分为表面阻力的线性阻尼D和波浪等非线性二次阻尼Dn(|v|)两个部分。

D(|v|)=D+Dn(|v|)

(34)

文献[1]所假设的AUV系统具有良好的对称性，因此

D(|v|)=-diag{Xu,Yv,Zw,Kp,Mq,Nr}-

diag{Xu|u||u|,Yv|v||v|,Zw|w||w|,Kp|p||p|,

Mq|q||q|,Nr|r||r|}

(35)

2.3 环境干扰

τenv∈R6×1，表示外部环境对AUV系统的力和力矩的干扰，干扰的形式和作用较复杂，一般在水下AUV系统的应用中，将各种干扰假定为线性可加的，因此风、浪、流都可以分开讨论加以叠加。

对于本系统中，风、浪、流不作为水动力模型的一部分，仅作为干扰等不确定因素在各种控制器设计中进行考虑，特别是对于水面USV和浅水应用的UUV，风、浪的影响非常大。实际应用中，考虑外部干扰波浪流动速度，则动力学模型为：

(36)

其中，vr是AUV系统相对于流体的速度，vr=ν-vc，其中vc是波浪速度，假设：

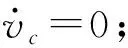
2)vc相对于AUV系统的速度ν为较小数值，近似有CA(ν)ν=CA(vr)vr；

此时，动力学模型为：

Mvr+C(vr)vr+D(vr)vr+g(η)=τenv+τ

(37)

在常规情况下，流体仅有线速度，没有旋转角速度，因此，流体速度为

(38)

2.4 AUV系统推进器建模

AUV系统的推力力矩τpro，由文献[1]可知，推进器的推力是航行器的速度向量ν和控制输入向量u的非线性函数，其中ν是相对于海浪的速度，u是控制输入力矩。

τpro=B(ν)u

(39)

细节计算：B的计算。

τpro=ρD4KT(J0)|u|u(J0)

(40)

J0=Va/(uD)

(41)

(42)

T(u,Va)=T|u|u|u|u+T|u|Va|u|Va

(43)

Q(u,Va)=Q|u|u|u|u+Q|u|Va|u|Va

(44)

τpro=Bu

(45)

其中D是叶桨直径，KT是推进系数，可以由系统桨叶数据推导出。

3 六自由度系统模型

AUV系统在环境中做6DOF的运动，式(46)可以用来描述系统的动力学特性

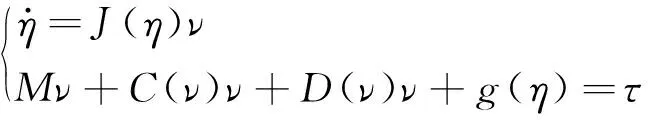
(46)

其中：

M=MRB+MA

C(v)=CRB(v)+CA(v)

D(v)=D+Dv(v)

根据式(27)，AUV系统的速度较低，忽略科氏力和向心力的作用，且AUV系统运动方式主要有前进、后退、上浮、下潜和转艏，因此，可以将其视为简单的单自由度运动[9]，各运动自由度耦合较小，且互不干扰。

4 AUV系统模型的仿真分析

对所建立的AUV系统模型进行仿真分析如图2所示，由于系统模型处于临界平衡状态，因此Z轴存在一定的不平衡力矩，在开环状态下，AUV系统的坐标Z轴存在一定速度，使系统Z轴的坐标发生改变。

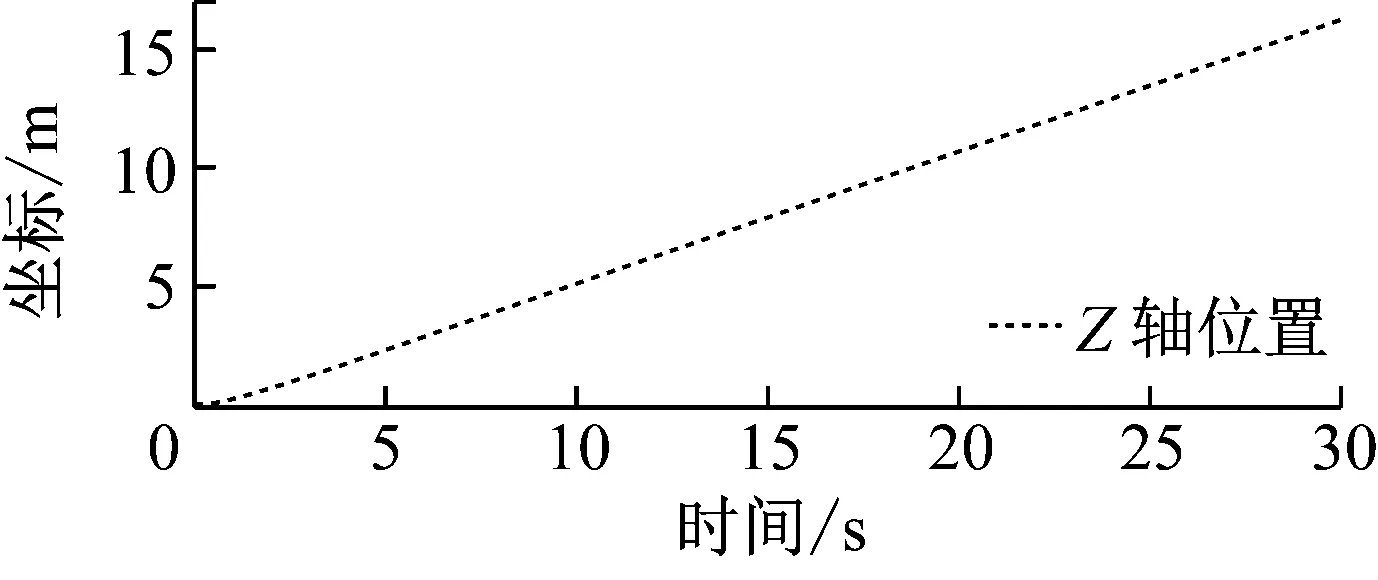
(a)

(b)

AUV系统在实际应用中，一般会保持一个稳定的航向速度，因此速度控制是基本控制，此处采用PID控制器进行闭环控制速度，surge的速度控制效果如图3所示，可见，速度控制具有超调，且在5 s时间范围内达到稳态，当速度发生变化时，系统仍然会有超调，且会达到稳定状态。

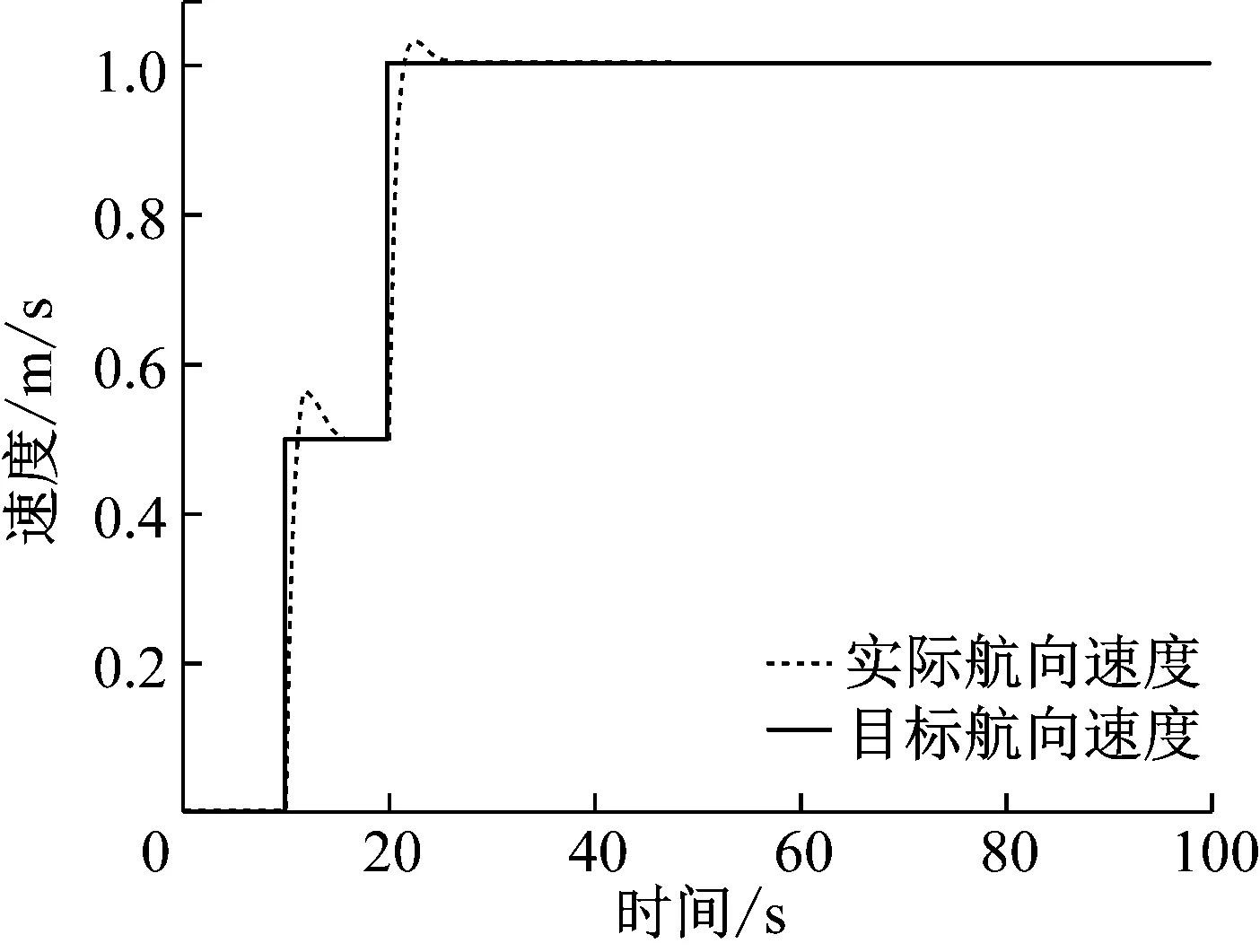
图3 航向角度动态响应

AUV系统在水下运行时，需要有固定的航向目标，或者航向目标发生变化时，可以进行调整，因此，对AUV系统进行航向角度控制，航向角度仿真如图4所示，在t=30时，目标值设定为5 deg，AUV系统可以快速跟踪上目标角度，虽然存在一定超调和系统运行过程中存在波动，但是超调和波动都在可以接受范围之内。

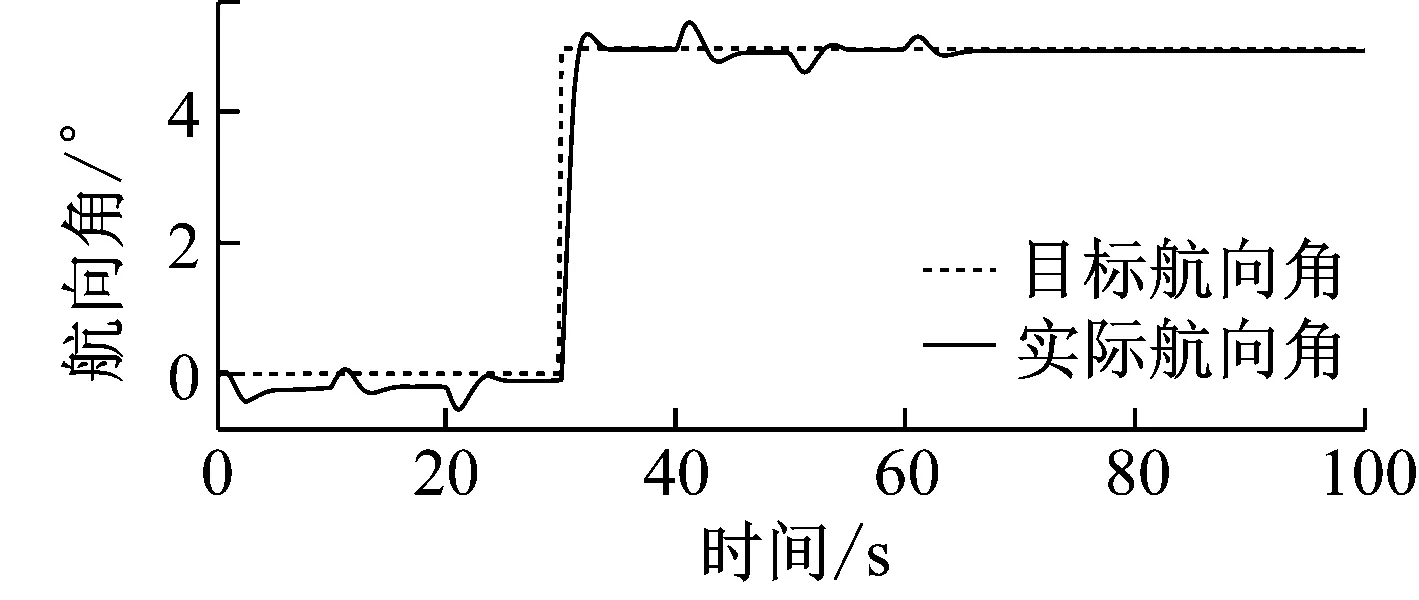
(a)

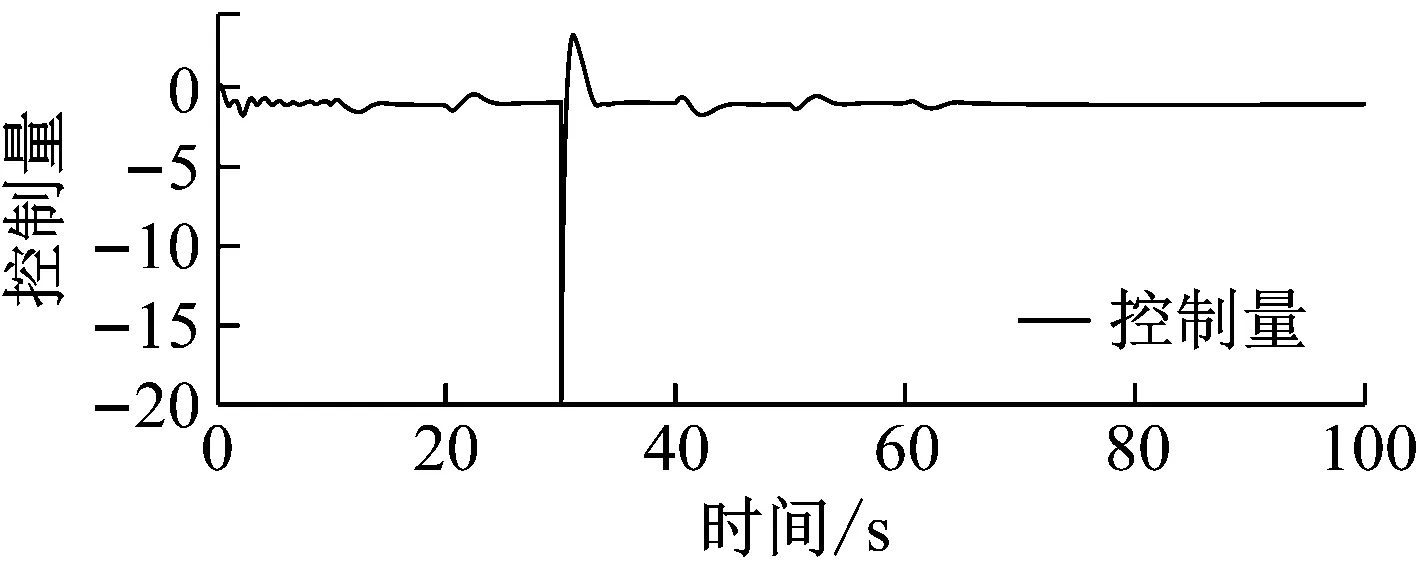
(b)

5 结束语

实验结果表明，本文所建立的AUV 系统模型，既考虑运动学参数，也考虑动力学参数，且对各种参数进行细化，适用于程序的过程设计；根据开环动态测试可见，系统运行结果符合Z轴存在不平衡力矩的结论；根据动态航向速度和航向角度仿真分析可见，系统模型响应速度满足实际设计要求，因此系统模型设计可以用于测试环境的设计。