交通干线信号灯配时的公共周期优化方法
2022-11-04党璠煜樊秀梅张兴辉
党璠煜,樊秀梅,张兴辉
(西安理工大学自动化与信息工程学院,西安 710048)
随着社会经济的发展和人民生活水平的不断提高,汽车逐渐在人们的日常生活出行中普及,在给人们出行带来便利的同时也给能源、环境及交通带来巨大压力。由于修建高架桥、拓宽原有道路等传统的缓解交通拥堵的方式容易受到现有道路设施和土地资源的限制,因此通过优化交叉口信号灯配时策略对交通流进行合理化、智能化管控,成为提高交通运行效率、改善交通拥挤状况的主要手段。在城市交通道路中,各交叉口之间相互关联紧密,且大多数情况下车流集中在主干线,为改善城市整体交通路网的通行能力,实现多交叉口的协调控制是城市交通发展的必然方向[1],其主要思想是将干线上连续的交叉口看成一个整体,通过协调各交叉口信号灯之间的关系,使车辆尽可能多地遇到绿灯并顺利通过多个连续交叉口,从而形成一定的绿波带[2-3]。
交通控制主要是依据交叉口上下游的交通流参数,确定信号灯的周期、绿信比和相位差,给予不同进口方向车辆时间分配通行权,从而实现车辆在交叉口安全、有序、高效通行。信号周期被认为是交通管理与控制中的重要参数,因此,对交叉口信号周期进行分析与优化可以有效改善交叉口的车辆通行。近年来,在对交叉口交通信号配时参数进行改进研究时,多目标优化方法得到了广泛的应用。牟海维等[4]在改进的Webster模型基础上,提出了以车辆延误、行人延误停车率、通行能力、行人平均延误和尾气排放为优化指标的多目标函数,并利用改进的粒子群算法分别对高峰期、低峰期的最佳周期进行求解;成卫等[5]采用RBF(径向基函数)神经网络模型预测交叉口晚高峰的交通流量,并建立了以平均车辆延误和车辆平均停车率为主要控制目标的多目标优化模型,对交叉口信号周期时长进行优化;Mou[6]在对非饱和交通流下的信号配时方案进行优化时,建立了关于道路通行能力、车辆延误和停车次数的多目标优化模型,并利用改进的蜻蜓算法对其进行求解;Kou 等[7]通过实际数据估算了不同车辆类型的排放率,考虑车辆排放与交通通行效率的关系,建立了关于车辆延迟、停车次数和尾气排放的多目标优化模型,并利用遗传算法进行求解;Zhao 等[8]以车辆延误和停车次数为单个交叉口信号配时优化的目标,在饱和度和信号周期范围的约束下,建立了非饱和交叉口多目标优化模型,并采用非支配排序的人工蜂群算法进行求解;刘美妮[9]以交叉口通行能力和车辆平均延误为目标,以相位有效绿灯时间为决策变量,建立了公共周期和绿信比的联合优化模型;李元[10]利用分层控制的思想,将干线协调控制分为两层进行研究,其中交叉口控制层采用改进的两级模糊控制器,使绿灯延时单元可以根据到达和驶出交叉口的车流量动态变化与切换,系统协调层采用经遗传算法优化后的模糊控制器对公共周期和各路口相位差进行优化。
目前,大多数多目标优化方法都是针对单个交叉口进行优化,且在对干线中的信号周期进行计算时仍主要沿用经典的韦伯斯特配时法,再从中选取最大值作为公共周期。这种方法在一定程度上改善了车流量较大的交叉口的控制效果,提高了整体通行能力,却忽略了增加周期时长会使其他交叉口的车辆延误增多。因此,本文以干线协调控制为研究背景,采用多目标优化方法对公共周期进行优化,并利用遗传算法对其进行求解,从而与绿灯时长、相位差的优化形成递进关系,使干线协调控制能更好地发挥作用。
1 公共周期可调整范围优化
1.1 考虑交叉口间距的信号周期优化
在干线协调控制中,公共周期的确定方法为:先利用单点定时信号控制的配时方法计算各交叉口的信号周期,再从中选取最大值作为干线系统的公共周期。以F-B法为例,各交叉口的最佳信号周期计算公式为
(1)
式中,Ci为交叉口i的最佳信号周期,s;Li为交叉口i单个周期总的损失时间,s;Yi为交叉口i总的交通流量比之和。
F-B法以车辆总延误最小为优化目标对信号周期进行求解,但在实际交通道路中,双向交通的道路占绝大多数,若要取得最佳的绿波控制效果,干线上相邻交叉口之间的距离需满足下式:
(2)
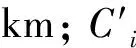
综合考虑车辆延误和交叉口间距对信号周期的影响,分别赋予其相应的权重[11],系统的公共周期可表示为
(3)
式中,C为信号周期长度,s;α、β为权重因子,取值为0~1,实际应用时根据具体情况而定,本试验中α、β取值分别为0.7、0.3。
1.2 基于车辆延误和通行能力的公共周期优化
大多数信号周期的计算方式都是基于某一段时间内检测装置收集的交通流数据确定数值,但由于交通流具有多变性和实时性,因而信号周期的数值也会在一定范围内波动。在多目标优化问题的求解过程中,信号周期作为约束条件之一,其最大值和最小值通常为给定的极值,而不是根据实际交通流推算得出,这会使信号周期的约束作用有所减弱。为此,本文通过分析信号周期与车辆延误、通行能力的关系,确定公共周期的可调整范围,同时为多目标优化问题的求解提供约束条件。
1.2.1 信号周期与通行能力的关系
道路通行能力是指在给定各种道路条件下的指定时间内通过某一横断面的最大通行车辆数,对交叉口而言,某一相位的最大通行能力取决于饱和流量和周期绿信比,用公式表示为
(4)
式中,λ为绿信比;L为总损失时间,s;qc为饱和流量,pcu·h-1。
通过拟合,可以近似得出信号周期与通行能力的关系为
Cap=228.6lnC+522.72
(5)
1.2.2 信号周期与车辆延误的关系
1.地方性。在社会救助制度建立和发展过程中,地方政府所发布的政策文件起到了至关重要的作用。由地方政策框定社会救助权要件兼顾了地区经济发展、生活水平的不平衡,但与此同时,作为社会救助制度中心的社会救助权的地方化,也导致了社会救助体系的“地方割据”,造成了不存在全国意义上的社会救助制度,只存在地方意义上的社会救助制度,《社会救助法》的难产或也与此相关。
车辆延误是计算信号配时和衡量路口通行效果的一个重要参数,它是指交通冲突或信号控制设施的限制给车辆带来的时间损失。根据稳态理论,某一相位的车辆平均延误时间可表示为
(6)
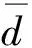
(7)
式中,qs为该相位实际交通量,pcu·h-1;qc为该相位饱和交通量,pcu·h-1;y为该相位的流量比;λ为该相位的绿信比,其计算公式为
(8)
式中,Y为交叉口总的流量比之和。
通过拟合,可以近似得出信号周期与车辆延误的关系为
(9)
分别分析信号周期与通行能力、车辆延误的关系可知:信号周期与通行能力为对数关系,信号周期较小时通行能力的增量较大,因而可通过此关系确定信号周期的最小值[9];信号周期与车辆延误为线性关系,信号周期增大时车辆延误也随之增大,因而可通过此关系确定信号周期的最大值。
在干线协调控制中,公共周期的变化范围是由各交叉口信号周期的变化范围共同决定的,并且公共周期的选取要使各交叉口的交通状态均得到有效协调。因此,公共周期的最小值、最大值分别为
(10)
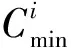
2 建立公共周期优化模型与求解
2.1 建立周期优化模型
在交通信号配时的优化过程中,优化目标主要有车辆延误、通行能力、排队长度、停车次数等。在交通流较小的情况下,优化目标主要是减少信号交叉口延误;而当交通流较大时,车辆在进口道的停止线附近容易形成排队车流,此时的首要优化目标是疏散车流,预防交通拥堵,提高交叉口的通行能力。综合考虑交通效率和性能指标,本文选择车辆延误和通行能力组合的双目标优化模型,并采用加权系数法转化为单目标优化模型进行求解。
由于评价车辆延误和通行能力指标的单位不同,因而首先需要对其进行无量纲化处理,指标的重要程度可以通过不同的权重来表示。建立该模型的最终目标是提高道路通行能力,缩短车辆延误时间,因此公共周期的双目标优化函数可表示为
(11)
约束条件为
(12)
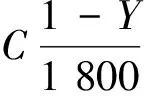
干线的车辆平均延误D和通行能力Cap的计算公式分别为
(13)
(14)
2.2 基于遗传算法的模型求解
由于无法通过传统的数学方法对上述建立的带有约束条件的双目标优化模型求解最优值,因此本文采用智能优化算法中的遗传算法对该模型进行求解。遗传算法是一种基于自然选择和自然遗传机制的搜索算法,通过不断计算各染色体的适应值,选择最好的染色体,从而获得最优解[12]。遗传算法鲁棒性强、搜索效率高,尤其适合处理传统搜索方法难以解决的复杂的非线性问题,在交通信号优化控制中具有良好的应用效果。遗传算法流程如图1所示,具体求解步骤如下:
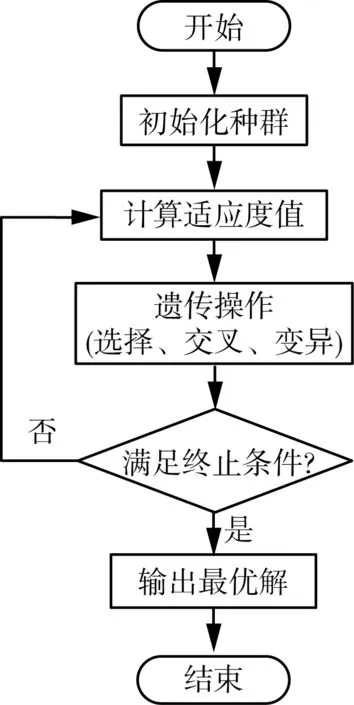
图1 遗传算法流程
步骤1:编码。本文采用实数编码方式,先根据约束条件确定信号周期、绿信比的范围,再对信号周期、绿信比进行实数编码,随机产生满足条件的种群个体,染色体的形式为C、λ1、λ2、λ3、λ4。
步骤2:确定适应度函数。个体的适应度越高,被选择的概率越大,因此本文在计算不同种群的适应度值时,选择目标函数的倒数作为适应度函数,适应度函数的计算公式为
(15)
步骤3:遗传操作。依次进行选择、交叉与变异操作,使问题的解多次迭代进行优化,不断逼近最优解。其中,选择操作时采用适应度比例法计算每个个体被选中的概率,交叉算子pc与变异算子pm均采用自适应算子,以提高迭代速度。
步骤4:迭代终止判断。当找到最优解或达到设定的最大迭代次数,则迭代停止,输出最优公共周期解,否则返回步骤2,继续迭代。
3 实例验证
为验证本文所提出的公共周期优化方法的有效性,在微观交通仿真平台VISSIM4.30中搭建以四个交叉口组成的干线系统进行仿真分析。设东西方向为干线,南北方向为支线,相邻交叉口的间距分别为350 m、400 m、420 m,道路为双向六车道,车道宽度均为3.5 m,且所有交叉口均采用两相位信号控制策略。干线交通模拟场景如图2所示,两相位交叉口控制方案示意如图3所示。
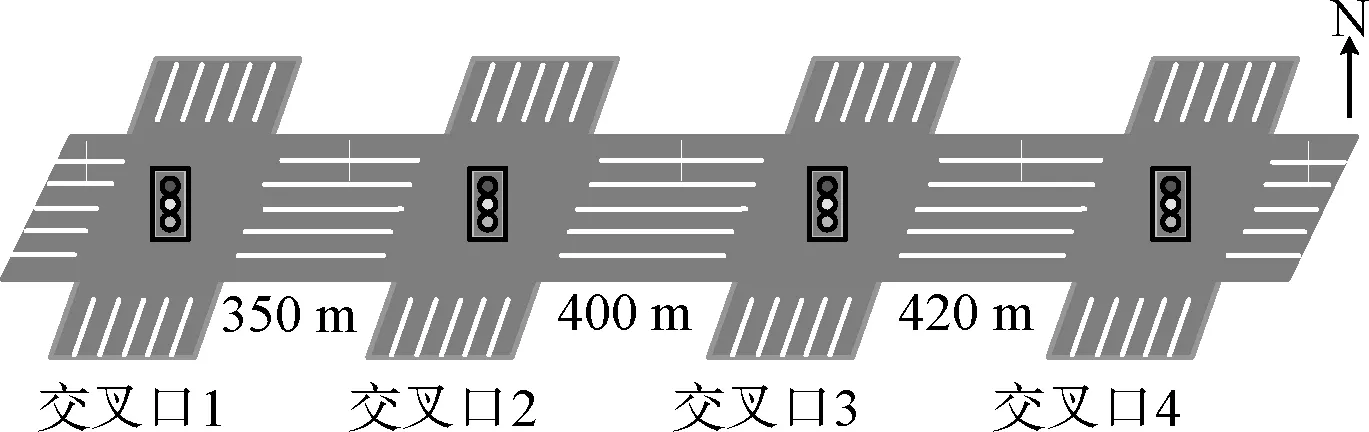
图2 干线交通模拟场景
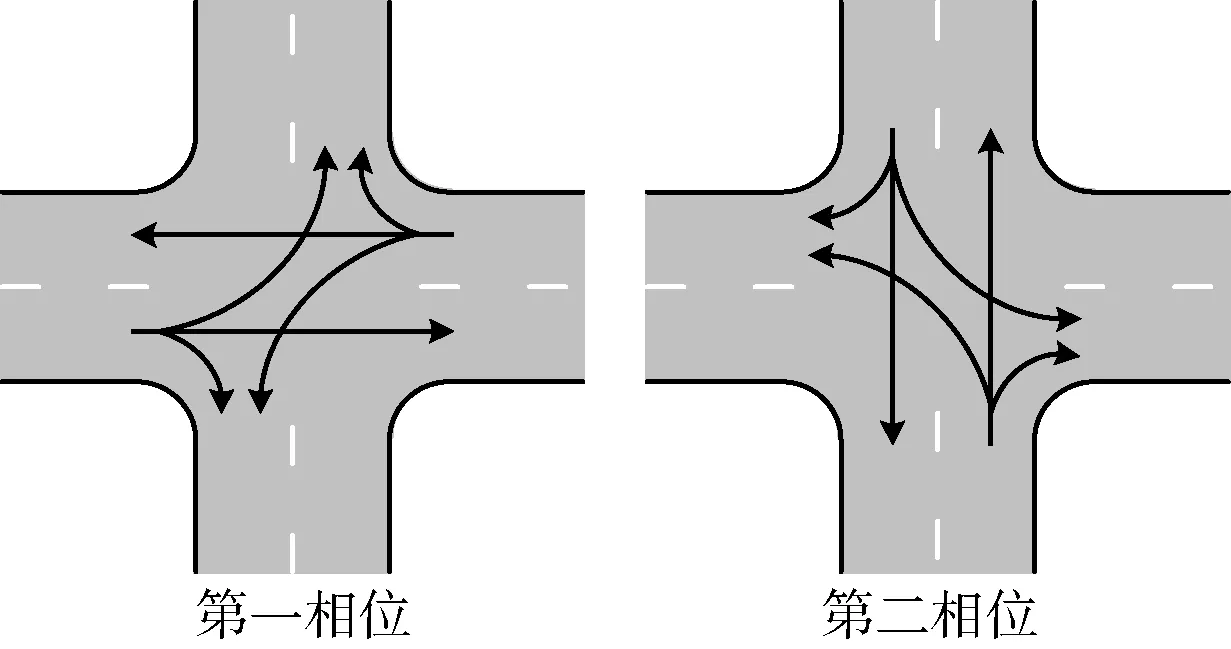
图3 两相位交叉口控制方案示意
3.1 仿真参数设置
交叉口各进口道车流量分布如表1所示,道路上有小型汽车、重型货车和公交车三种车型,车辆占比分别为60%、10%、30%,期望车速分别为80 km/h、60 km/h、60 km/h,三种车型车辆直行、左转、右转的比例分别为50%、20%、30%,初始随机种子为40,仿真时长设置为3 600 s,每隔900 s进行一次数据采集,仿真过程中不考虑行人和非机动车辆对行驶车辆的影响。
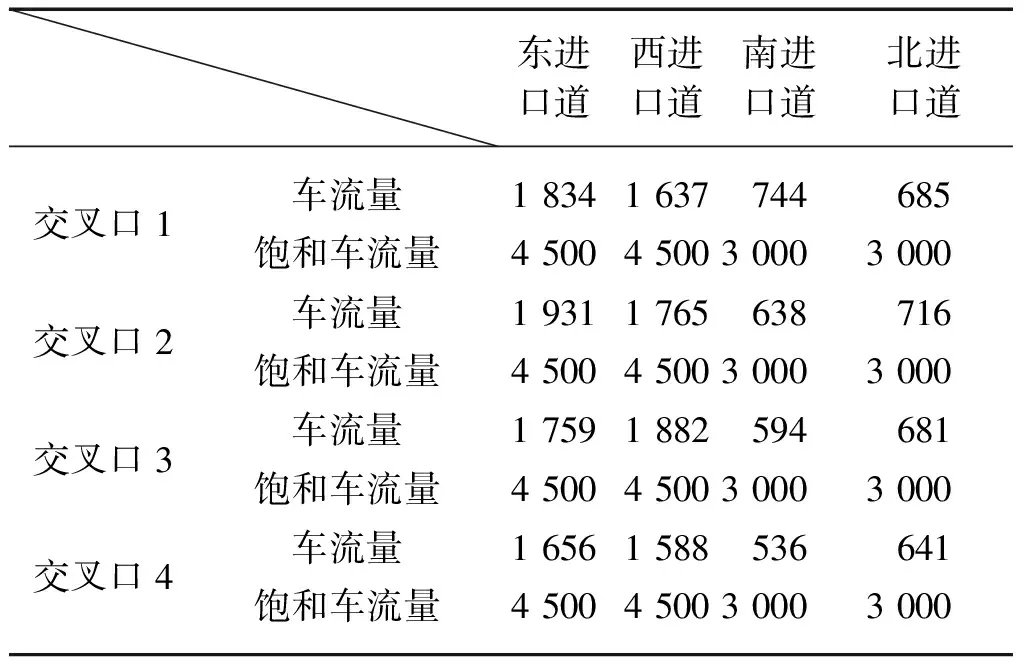
表1 交叉口各进口道车流量分布 (pcu/h)
3.2 仿真结果
在VISSIM中搭建干线路网,根据实际调研和相关参数设定车流的构成与分布;配置信号灯,分别利用公共周期优化前后的配时方案计算信号周期与绿灯时长,再利用数解法计算相邻交叉口的相位差;设置系统评价参数,在干线道路的上行方向和下行方向分别设置检测点共计8个,并对干线道路车辆延误、通行能力这两个评价指标进行数据采集。
本试验在MATLAB中调用VISSIM的COM接口功能,启动整个干线系统的仿真。考虑到交通流的随机性,采用连续仿真模式,使随机种子每次加1,对5个不同随机种子下的数据进行采集,得到优化后的仿真结果。干线车辆延误对比如图4所示,干线通行能力对比如图5所示。

图4 干线车辆延误对比
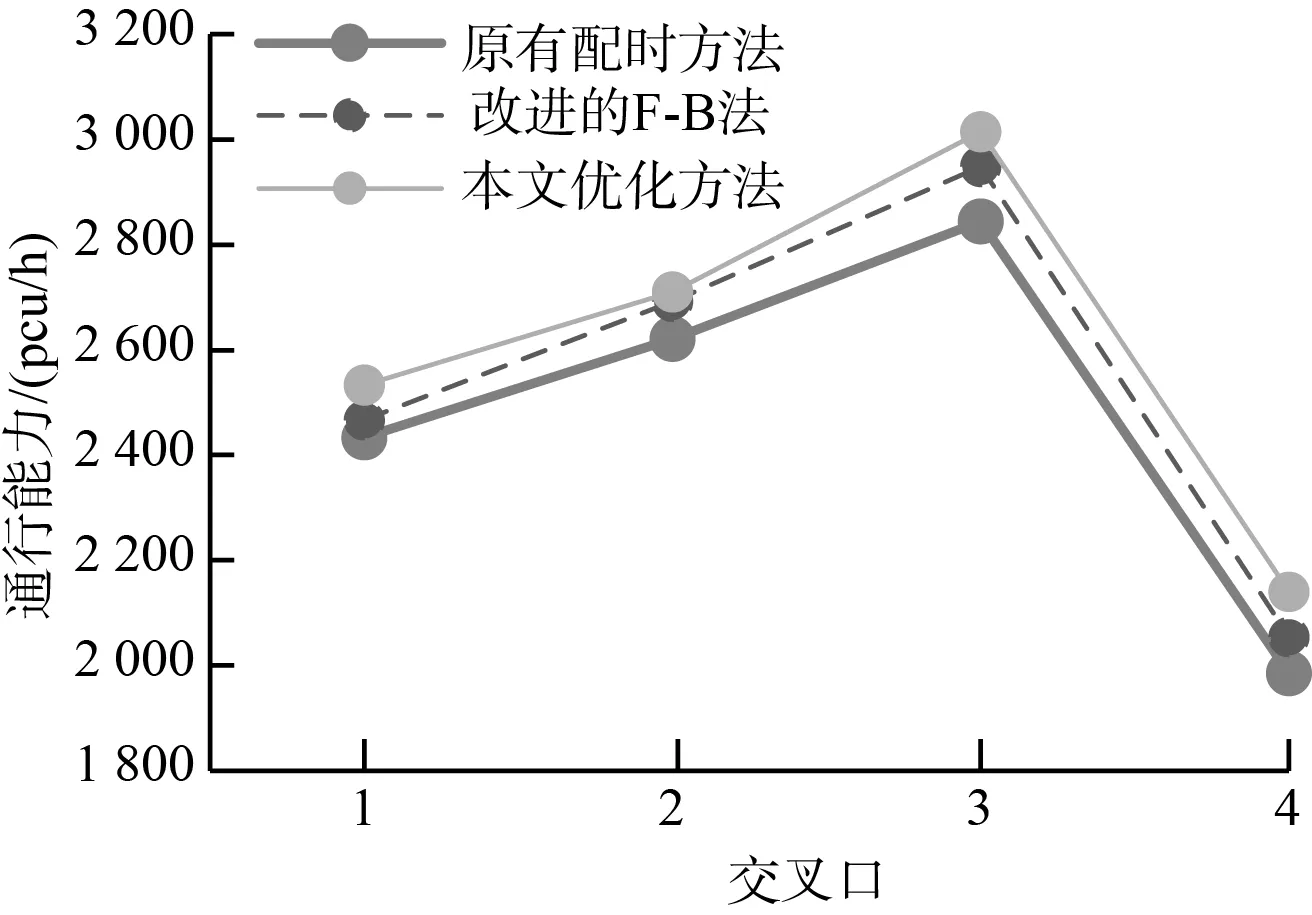
图5 干线通行能力对比
对干线上各交叉口的评价指标进行统计求均值,不同方法仿真结果对比如表2所示,由表2可知,本文所提出的公共周期优化方法相比原有配时方法,在车辆延误上降低了17.0%,在通行能力上提高了5.2%;相比改进的F-B法,在车辆延误上降低了11.2%,在通行能力上提高了2.1%。

表2 不同方法仿真结果对比
4 结语
本文通过分析信号周期与车辆延误、通行能力的关系,确定公共周期的可调整范围,建立了关于公共周期的双目标优化模型,再利用遗传算法对模型进行求解,并通过试验验证其有效性,结果表明:本文所提出的公共周期优化方法相比原有配时方法,在车辆延误上降低了17.0%,在通行能力上提高了5.2%;相比改进的F-B法,在车辆延误上降低了11.2%,在通行能力上提高了2.1%。之后的研究可以从更多角度出发,分析不同评价指标与信号周期之间的关系,例如停车次数、尾气排放等;也可以在本文的研究基础上,进一步对干线系统的绿灯时长和相位差依次进行优化,从而使车辆尽可能连续通过多个交叉口,提升干线整体的通行效率。
