桥面铺装协同受力的空心板梁抗弯承载力研究
2022-11-04徐志华彭德清汪晓红舒伟伟欧阳秋皓黄小文
徐志华, 彭德清, 汪晓红, 舒伟伟, 卢 漉, 欧阳秋皓, 黄小文
(1.江西省交通工程集团有限公司, 南昌 330038; 2.华东交通大学 土木建筑学院, 南昌 330013; 3.江西省天驰高速科技发展有限公司, 南昌 330103)
先张法预应力混凝土空心板梁因其施工工艺简单、结构自重轻、混凝土用量少,在我国中小跨度桥梁中应用广泛。为保护空心板梁体、分散车轮集中荷载、提高桥梁耐久性与提高行车舒适性,通常在空心板梁桥上方浇筑一层钢筋混凝土铺装层[1-2],但在以往研究中,一般将桥面铺装层作为构造层来考虑[3],不考虑铺装层对主梁抗弯承载力的影响。实际工程中,由于混凝土桥面铺装层与主梁粘结紧密并与主梁共同受力,具有改变结构承载力的能力[4-5],故铺装层对主梁抗弯承载力的影响不可忽视。
大量学者对带铺装层混凝土的桥梁进行了研究。周威等[6]开展了设置铺装层与无铺装层的预应力混凝土双T板和空心板梁的弯曲性能试验,发现设置铺装层能明显提高梁体承载力。任森智等[7]对比了梁体顶升法、加厚铺装层法和改造铺装层法3种加固方案,发现改造铺装层经济实惠且方便施工,能够很好地达到设计要求承载力。许国平[8]对带桥面铺装层的空心板桥通过有限元分析及荷载试验研究发现,考虑桥面铺装层参与主梁受力后更接近实测数据。王鹏等[9]对钢筋混凝土简支T梁进行了加固研究,发现增设铺装层加固更有利于提高梁的承载能力。唐国斌等[10]通过对实梁的破坏性试验,研究了铺装层对主梁承载力的影响,结果表明桥面铺装层能与主梁共同受力,极限承载力得到显著提高。王锋[11]通过整体化铺装加固前后的模型试验对比发现,铺装层能将荷载有效地传递给空心板,与梁体协同受力,提高其承载能力。
查阅已有研究成果,主要集中于带铺装层结构的梁体结构承载力试验,对铺装层协同受力的空心板梁抗弯承载能力计算方法研究较少。本文基于平截面假定,对桥面铺装层共同参与受力的先张法预应力混凝土空心板进行了分类,推演了适筋梁抗弯承载力的理论公式,分析了考虑桥面铺装协同受力对预应力混凝土空心板梁受力性能的影响,并通过实际桥梁工程中含有桥面铺装层的先张法预应力混凝土空心板梁承载力试验验证了本文抗弯承载力理论计算研究结果。
1 基本假定与截面简化
1.1 基本假定
实际预应力混凝土空心板梁中,桥面铺装层与预应力混凝土空心板梁的协同受力异常复杂。为简化其抗弯承载力计算的方法,特进行以下基本假定:
1) 考虑桥面铺装层协同受力的预应力混凝土空心板梁正截面抗弯破坏时,截面应变满足平截面假定。空心板梁桥施工时,将空心板顶部凿毛成凹凸不平的接触面,表面清洗干净后浇筑铺装层混凝土[12]。该施工工艺满足了预应力混凝土空心板梁与桥面铺装层之间的抗剪需求,桥面铺装层局部受力与动力效应不影响协调受力和变位[13]。因此,含有桥面铺装层的预应力混凝土空心板梁正截面抗弯破坏时,满足平截面假定的基本要求。
2) 预应力混凝土空心板梁被设计为适筋梁。考虑铺装层协同受力后,只增加截面高度与受压区面积,不会改变其适筋破坏的特征。
3) 在推演抗弯承载力计算公式时,忽略受拉区混凝土抗拉影响,受压区混凝土应力-应变关系按《混凝土结构设计规范》(GB 50010—2010)确定。
4) 仅考虑预应力钢筋对正截面抗弯承载力的贡献,不考虑空心板梁与铺装层中普通钢筋的影响,同时忽略空心板梁桥其余附属结构对承载力的影响。
1.2 截面简化
基于以上基本假定,公路桥梁中先张法预应力混凝土空心板梁的横截面,可划分为桥面铺装层、铰缝、主梁及内部空心圆、预应力钢绞线5部分,如图1所示。
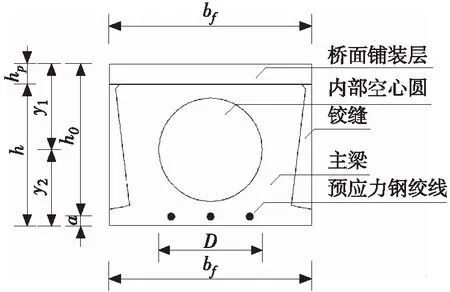
图1 混凝土空心板截面示意
由于桥面铺装层混凝土等级与空心板梁混凝土等级不同,需进行一定的简化。处于适筋破坏的带铺装层空心板梁,其极限抗弯破坏时主梁与铺装层混凝土均达到了极限压应变,混凝土的强度达到了极限抗压强度。为简化计算,根据桥面铺装层极限抗弯承载力相等的原则,将铺装层混凝土换算成空心板强度相同的混凝土,即
(1)
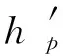
由式(1)可得到桥面铺装层混凝土换算后的厚度:
(2)
在预应力混凝土空心板梁桥中均有铰缝,主要起横向抗剪连接作用,对空心板纵向承载力影响甚微[14-16]。因此,本文忽略铰缝对空心板承载力的影响。
空心板梁含有内部空心圆,如图1所示,若采用内部空心圆的曲线变宽度截面,则造成抗弯承载力表达式异常繁琐。为此,将空心板梁等效为工字形截面,如图2所示。按照等面积、等形心位置及惯性矩不变的原则,将圆形孔等效为工字形截面的矩形孔,得到换算后2个宽为bk、高为hk的矩形孔:
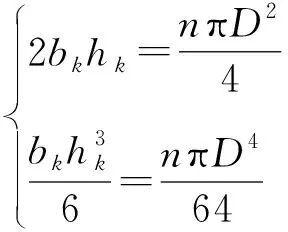
(3)
式中:D为圆形孔直径;n为孔洞个数。
由式(3)可得到矩形孔换算后的宽度与高度为:
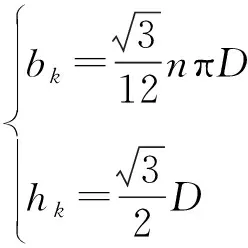
(4)
根据形心位置不变的原则,可得上下翼缘高度与腹板宽度为:
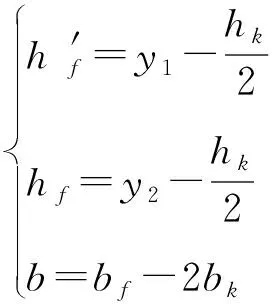
(5)
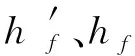
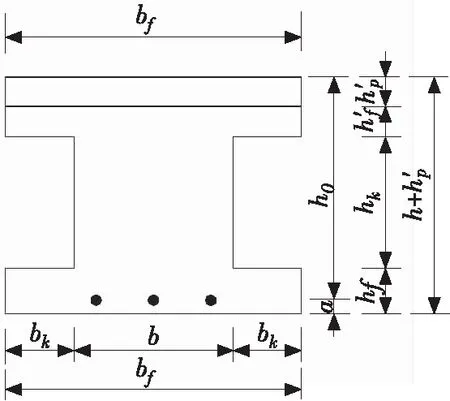
图2 截面简化示意
2 桥面铺装协同受力的空心板抗弯承载力计算
2.1 截面类型划分
根据混凝土受压区高度的不同,可将带铺装层预应力混凝土空心板梁分为2类:
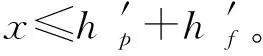
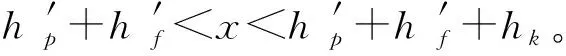
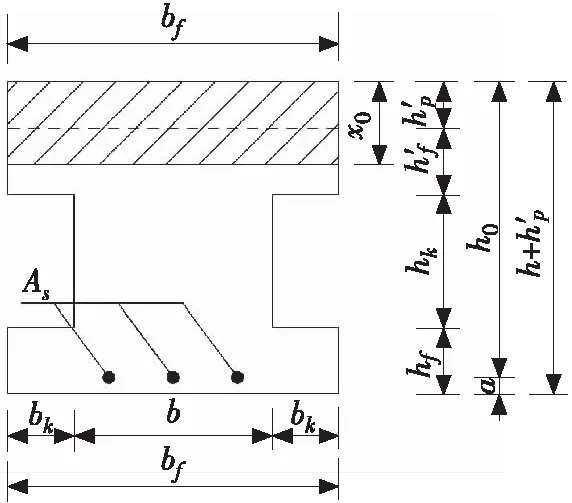
(a) 第1类工字型截面
2.2 第1类工字形截面抗弯承载力计算
当桥面铺装协同受力的预应力混凝土空心板梁为第1类工字形截面时,其抗弯承载能力极限工况下截面受力如图4所示。
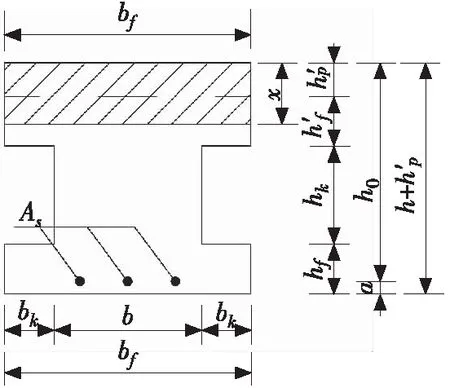
(a) 主视
此时,中和轴在工字形截面上翼缘内,根据截面水平方向受力平衡条件可得:
(6)
式中:fsd和As分别为受拉区预应力钢绞线的抗拉强度设计值和截面面积。
式(1)为第1类工字形截面的判断条件,此时,混凝土受压区高度应按式(7)计算:
fcdbfx=fsdAs
(7)
由式(7)可得:
(8)
根据截面弯矩平衡条件,可得到第1类工字形截面抗弯承载力为:
(9)
式中:Md为弯矩设计值;h0为带铺装层空心板截面有效高度,其值按式(10)计算:
(10)
式中:h为空心板梁高度;a为钢绞线合力点至受拉区边缘的距离。
将式(8)、式(10)带入式(9),可得:
(11)
式(11)为考虑桥面铺装协同受力下预应力混凝土空心板梁第1类截面抗弯承载力的计算。
2.3 第2类工字形截面抗弯承载力计算
当中和轴位于换算后工字形的腹板内时,其抗弯承载能力极限工况下截面受力如图5所示。
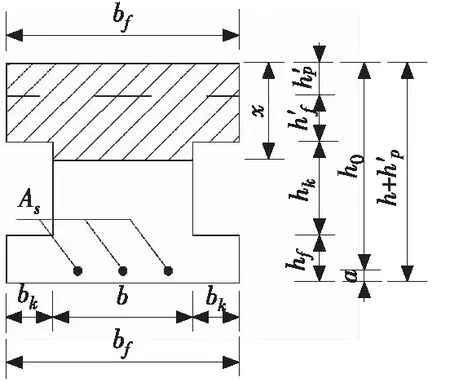
(a) 主视
此时,中和轴在腹板内,根据截面水平方向受力平衡条件可得:
(12)
式(12)为第2类工字形截面的判断条件,由截面受力平衡条件可得:
(13)
由式(13)可得第2类工字形截面混凝土受压区高度:
(14)
根据截面弯矩平衡条件,可得到第2类工字形截面抗弯承载力为:
(15)
将式(14)带入式(15),可得:
(16)
式(16)为考虑桥面铺装协同受力下预应力混凝土空心板梁第2类截面抗弯承载力的计算。
2.4 不考虑桥面铺装协同受力的空心板梁抗弯承载力计算
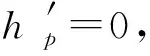
(17)
第2类工字形截面的判断条件为:
(18)
同理,可得不考虑桥面铺装协同受力空心板梁第1类工字形截面抗弯承载力的计算式为:
(19)
第2类工字形截面抗弯承载力的计算式为:
Md=fsdAs(h-a)-
(20)
3 桥面铺装协同空心板受力对空心板梁承载力的影响
3.1 对截面类型的影响
由式(6)、式(12)、式(17)与式(18)可以看出,是否考虑桥面铺装与空心板梁协同受力,会造成空心板梁的截面类型判定条件产生变化。为研究该变化的具体表现形式,选取实际工程中4种典型跨径的预应力混凝土空心板梁,4种跨径空心板梁及铺装层结构材料均为C40混凝土,预应力钢绞线为Φj15高强度低松弛预应力钢绞线。根据相关设计资料获得桥面铺装层厚度通常在10 cm~14 cm之间,本文选取铺装层厚度为10 cm,以分析相同厚度的铺装层对不同跨径空心板梁的影响。空心板梁截面尺寸如表1与图6所示。
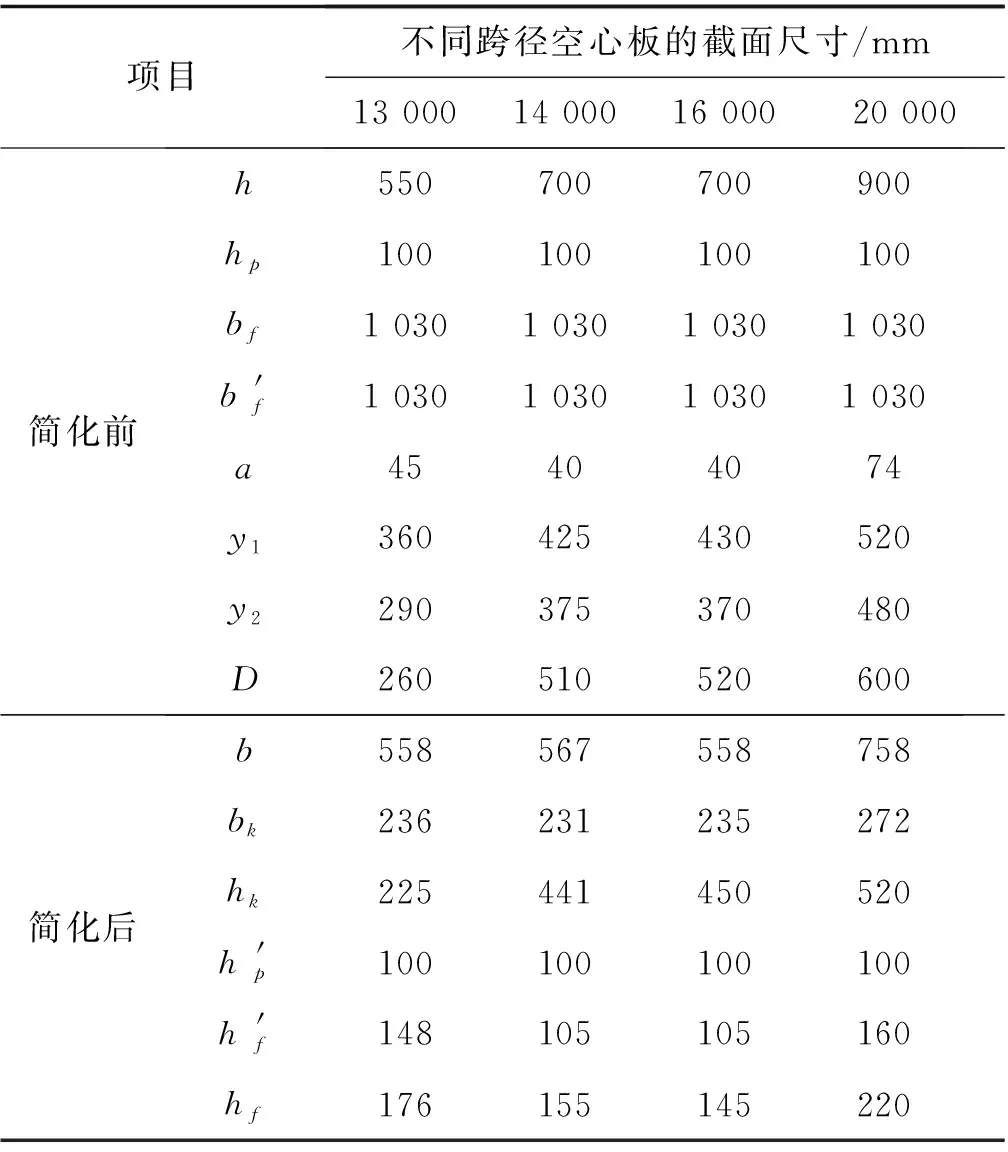
表1 4种常见空心板梁截面尺寸
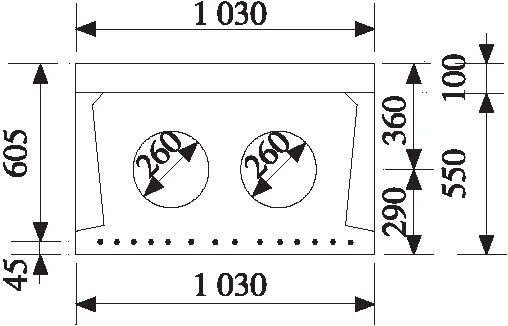
(a) 跨径13 m
使用铺装层协同受力空心板梁截面类型判断标准式(6)和式(12),与不考虑协同受力的空心板梁截面类型判别标准式(17)和式(18),分别计算中和轴高度并判断截面类型,两者对比结果如表2所示。
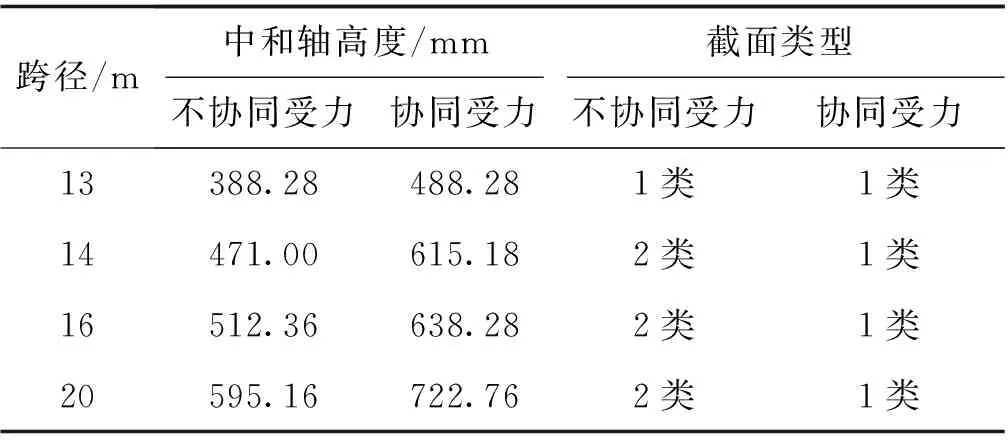
表2 截面类型对比
由表2可见,桥面铺装协同受力后,4种跨径空心板梁的中和轴高度均有较大提高;桥面铺装不共同参与受力时,除跨径13 m外其他跨径均为第2类截面,表明空心圆部分处于受压区;桥面铺装协同受力后,4种跨径空心板梁均为第1类截面,表明受压区在桥面铺装层与空心板梁上部区域。该现象表明,铺装层协同受力后,截面中和轴上移,影响了截面受压区的分布类型。
3.2 对抗弯承载力的影响
铺装层协同受力后,空心板梁的中和轴及截面有效高度均发生了变化,进而引起截面抗弯承载力发生变化。为探索承载力变化的大小,使用式(19)与式(20)计算铺装层不共同受力空心板梁的抗弯承载力,采用式(11)与式(16)计算铺装层协同受力的空心板梁抗弯承载力,两者的结果比较如表3所示。
由表3可知,桥面铺装层协同受力后,4种跨径空心板梁正截面抗弯承载力均有较大幅度提高,并且承载力提高的幅度随着跨径的增大而降低。其中,跨径13 m空心板梁正截面抗弯承载力提高22.71%,跨径20 m空心板梁承载力提高14.47%。综合分析表3可知,桥面铺装协同受力后,预应力混凝土空心板梁抗弯承载力较铺装层不协同受力的空心板抗弯承载力普遍增加10%以上。
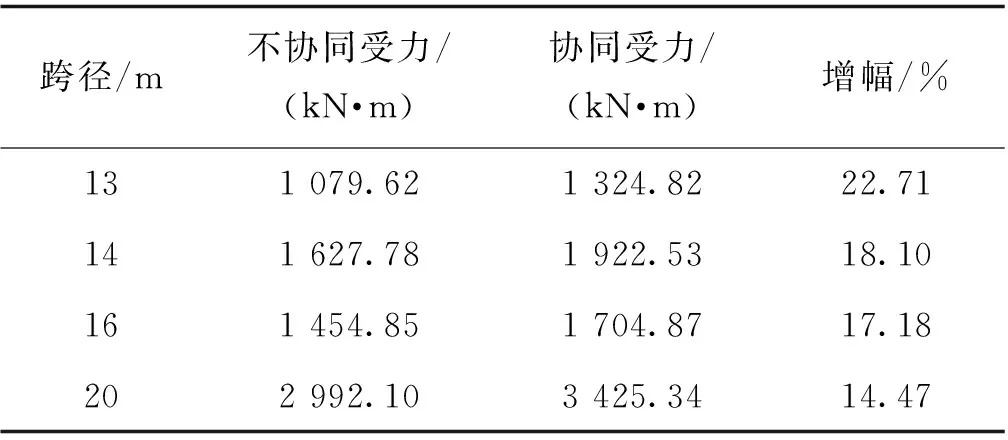
表3 铺装层协同受力对承载力的影响
4 抗弯承载力计算方法试验验证
4.1 试验概况
为验证桥面铺装协同受力对空心板梁正截面抗弯承载力的影响,对实际桥梁工程中带铺装层的预应力混凝土空心板梁进行静载试验,以验证本文抗弯承载力理论计算研究结果。
在南昌至九江高速公路改扩建工程施工中,利用绳锯切割法拆除了一片预应力混凝土空心板单梁,如图7(a)所示。绳锯切割法切面光滑平整,空心板梁完好,对其进行加载试验,测试其实际抗弯承载力。拆除空心板梁桥后,经测量,空心板梁全长14.2 m,截面尺寸如图7(b)所示。通过混凝土钻芯取样与预应力钢绞线取样,实测桥面铺装及空心板梁为C40混凝土,预应力钢绞线为16Φj15高强度低松弛预应力钢绞线。

(a) 空心板截面
本次静力荷载试验在江西某科技有限公司的桥梁结构实验室进行,试验加载及测试方案如图8所示。采用2个千斤顶在跨中两侧相距3 m的位置施加集中力,用于模拟纯弯梁受力区段。静力试验荷载采用分级加载,每级新增荷载10 kN,荷载持续5 min,变形与应变测试稳定后进入下一级加载测试。当变形持续增加而荷载不增加,或出现明显的破坏征兆时,停止加载并记录相应的荷载及测试结果。
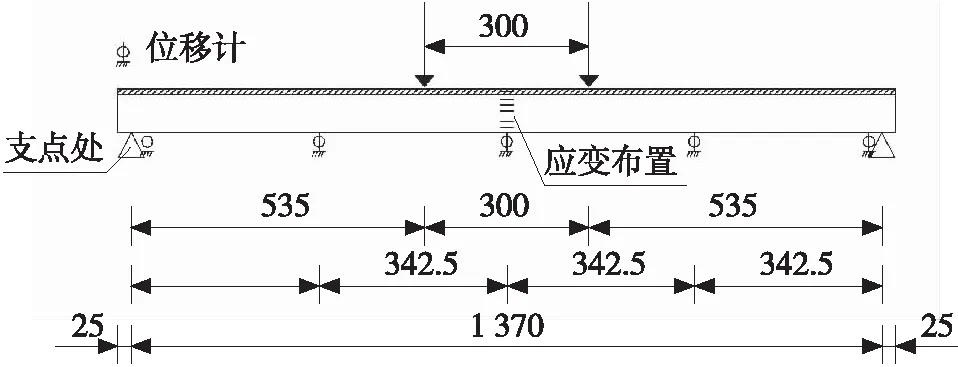
(a) 试验加载及测试示意
4.2 平截面假定验证
本试验在铺装层及空心板跨中侧面粘贴电阻应变片,通过测试不同荷载下截面各高度应变的变化,以验证本文提出的平截面假定。应变片粘贴位置如图9所示,应变测试结果如图10所示。
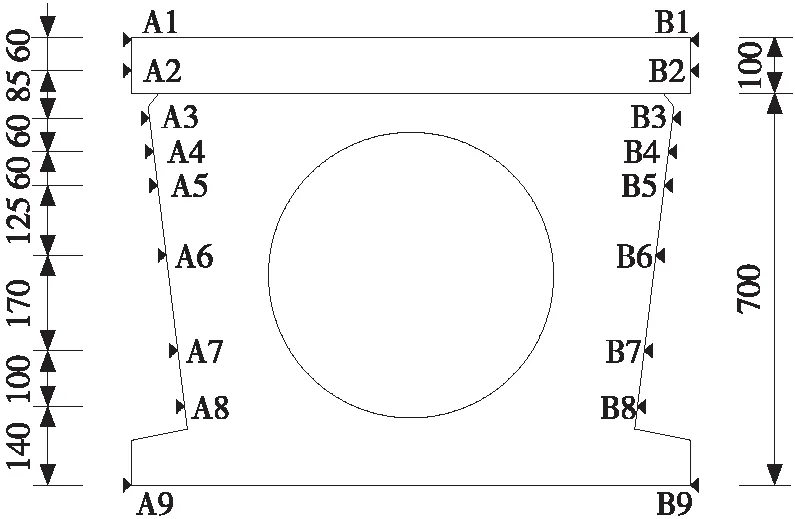
单位:mm
由图10可见,在每级加载中截面各位置的应变均与截面高度基本呈线性关系,验证了本文的平截面假定,特别是在桥面铺装层上的A1、A2应变测点与空心板梁其他位置的应变测点数据均呈线性关系,验证了本文基于铺装层与空心板梁结构界面无滑移基本假定的正确性。
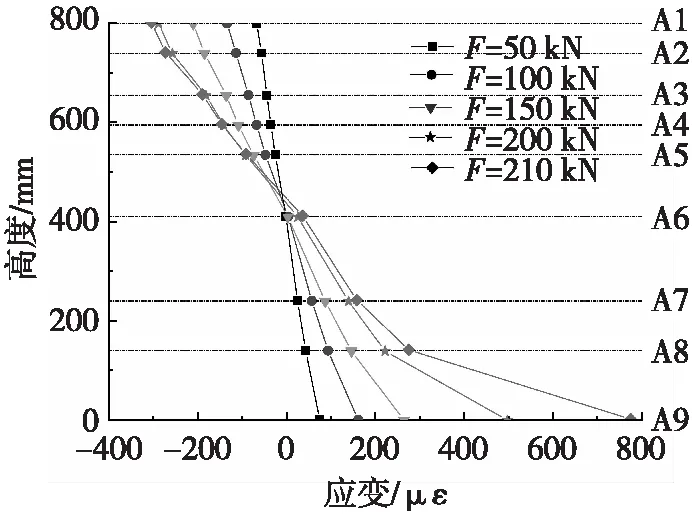
图10 空心板L/2截面应变
4.3 适筋破坏验证
当千斤顶加载至360 kN时,变形持续增加,带铺装层的空心板梁结构出现破坏现象,如图11所示。当空心板梁破坏时,铺装层和空心板之间连接紧密,未出现脱落与界面滑移现象;截面裂缝密集出现,细微裂缝延伸为贯穿裂缝,最大裂缝高度640 mm;铺装层混凝土出现压碎破坏征兆。综合抗弯承载力破坏现象可以看出,带铺装层空心板梁为适筋破坏。

图11 带铺装层预应力混凝土空心板梁破坏现象
4.4 承载力验证
通过记录每级加载荷载与相应阶段各点位移,得到带桥面铺装层空心板梁抗弯承载力试验的荷载-位移曲线,如图12所示。当荷载小于210 kN时,荷载与位移呈线性关系,表明此时结构受力呈弹性变形;当荷载为210 kN时,观察到首条裂缝出现;当荷载超过210 kN时,荷载与位移持续增加;当荷载达到360 kN时,结构破坏。
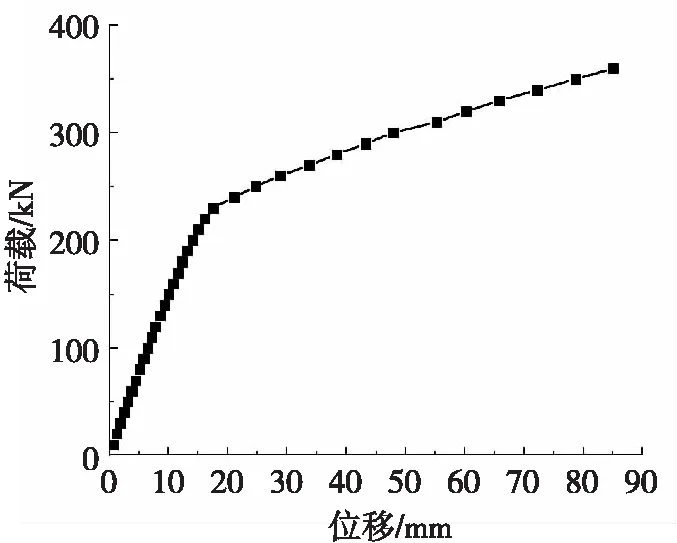
图12 荷载-位移曲线
按图8的加载试验,获得带铺装层空心板梁破坏时截面的极限弯矩和最大裂缝高度,并与根据本文弯矩承载力计算公式获得的极限弯矩及中和轴高度进行对比,结果如表4所示。
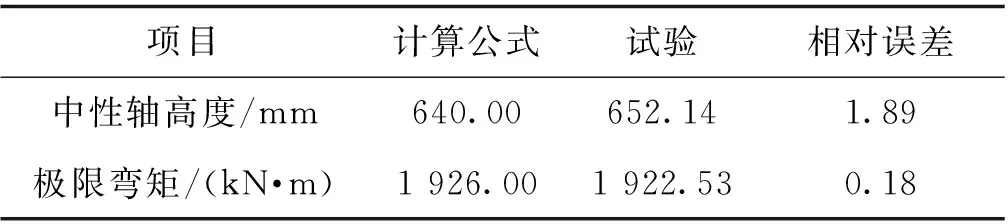
表4 理论计算与加载试验结果对比
由表4可以看出,本文理论方法的中和轴高度与极限承载力结果,均与试验方法结果吻合较好。其中,中和轴相对误差为1.89%,极限弯矩相对误差为0.18%,证明了本文理论公式的正确性。
5 结论
本文基于平截面假定,对考虑桥面铺装协同受力的预应力混凝土空心板梁进行了截面分类,推演了抗弯承载力的实用公式,分析了桥面铺装协同受力对空心板梁力学性能的影响,并通过抗弯承载力试验验证了理论计算成果,主要结论如下:
1) 提出的桥面铺装协同受力的预应力混凝土空心板梁极限承载力计算方法,与试验值吻合较好,相对误差仅有0.18%。
2) 考虑桥面铺装层协同受力后,铺装层和空心板之间连接紧密,不会出现脱落和界面滑移,满足平截面假定,破坏形态为适筋破坏。
3) 考虑桥面铺装层协同受力后,预应力混凝土空心板的中和轴位置上升,抗弯承载力普遍提高10%以上。
