基于Lattice算法的多智能车编队运动规划方法
2022-11-04常彦文邢晓龙
王 伟,常彦文,余 涛,雷 琦,邢晓龙
(1.北京石油化工学院信息工程学院,北京 102617;2.北京星航机电装备有限公司,北京 100074)
0 引言
近年来,自动驾驶技术不断取得新的进展,多车协同编队技术也引起了机器人研究界广泛关注。多车协同系统可以确保实现一个共同的任务目标,被广泛应用在搜索、运输等领域[1]。相比单车而言,多车不仅需要满足编队条件,还需要满足运动过程中导航和避障等其他约束条件,运动规划在导航和避障过程中扮演着重要角色。目前常见的运动规划算法分为三类:一是基于搜索的路径规划A*[2]和动态窗口法(DWA)[3]算法,通过对A*算法改进,不仅消除A*算法的冗余点,还融合了Lattice算法[4],能够满足车辆的非完整性约束,通过对DWA进行改进,修正速度窗口和三个现有评价函数,使多车系统在未知环境下保持队形[5];二是基于采样的路径规划RRT*[6]算法,针对复杂环境提出改进RRT的多机器人编队规划算法,通过在规划过程中加入多机器人之间位置约束,保证了多机器人在编队规划过程中队形保持不变[7];三是基于智能算法的路径规划遗传算法[8]和蚁群算法[9],通过构建机器人运动行为模型和协同行为模型,引入多蚁群系统改进信息素更新机制和状态转移方程,改进了蚁群算法,使多机器人在三维环境中协同行进[10]。这些算法的共同点在于在一定的约束条件下,选出车辆(机器人)从当前点到目标点的最优路径,这些方法在轨迹规划中得到了广泛的应用。但是这些方法也存在固有的缺点,例如:生成的轨迹形状有时候无法处理复杂的障碍约束;由于该方法没有考虑轨迹的最终状态约束[11],在非可执行轨迹的生成和评估中消耗了大量的计算资源,而且多车编队的运动规划还需要考虑各车辆的非完整性约束和位置约束。如何在结构化场景中动态地规划出符合车辆行驶的运动轨迹并且保证车辆的协同行驶是亟待解决的问题。
状态空间采样具有充分利用参考路径的几何约束和生成路径的空间分布一致性好的优点[12],吸引了大量学者的研究[13-14]。本文针对车辆非完整约束底盘,提出一种基于改进的Lattice算法的多车运动规划方法。
1 多车编队方法
本文在考虑多车编队队形的同时加入位置约束并且设计跟随、导航避障和等待的行为策略。跟随者能够根据感知信息动态变换跟随方式,并且兼顾编队队形保持和避障。
1.1 多车编队行为设计
本文针对多车在结构化环境编队行驶及避障,提出多车保持领航-跟随的编队模型。设计了领航者的导航、避障和等待行为;增添了跟随者的跟随、自主导航避障行为,并且通过位置约束调节跟随者的线速度和角速度。当跟随者感知到障碍物且编队模型无法规避时,选择自主导航模式;未感知到障碍物体时则继续选择编队模型位置约束保持队形,这使得编队避障更加灵活。多车编队行为框图如图1所示。
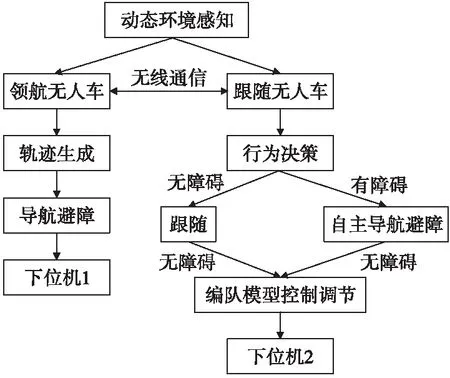
图1 多车编队行为框图Fig.1 Multi-vehicle formation behavior diagram
1.2 编队模型建立
本文以仿真环境中三台车保持三角阵型为例, 首先定义单车模型的非完整性约束模型,然后定义多车编队模型,最后将改进运动规划算法加入模型中,在Gazebo仿真环境下进行验证。
1.2.1单车辆模型
无人车模型属于典型的受非完整性约束的动力模型,其控制装置包括加减速和左右转向两个控制量,采用阿克曼转向结构。本文则利用车辆动力学模型对提出的改进算法进行验证,状态变量为(x,y,θ,v,φ),运动约束方程如式(1)所示,无人车运动模型如图2所示。
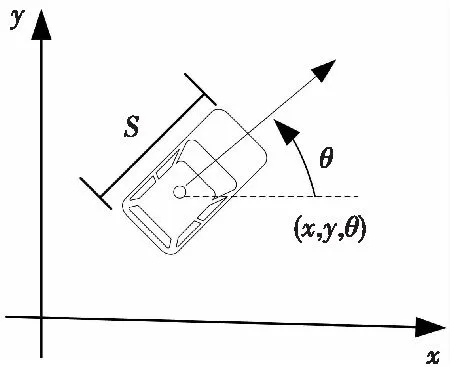
图2 无人车运动模型Fig.2 Motion model of unmanned vehicle
(1)
以小车的车身中点坐标(x,y)表示车辆在地图中的参考位置,θ表示小车的前进方向,v表示小车前进速度(单位:m/s),φ为转向角度,S为前轮轴到后轮轴之间的距离,小车的控制变量u1、u2分别为小车的加速度(单位:m/s2)和车轮转向速度(单位:rad/s)。由于小车是阿克曼转向模型,所以约束小车转向角度|φ|≤φmax,控制输入|u1|≤u1max,|u2|≤u2max。
1.2.2编队运动模型
以下针对有限信息设计距离-角度的编队运动模型,在xOy中描述无人车位姿,设(x,y)是无人车的位置坐标,θ为其方向角。给定一组无人车{F1,F2,F3,…},F1是领航者,其坐标位置向量为 [x1y1θ1]T,Fj是跟随者(j∈[2,n]),Fj坐标位置向量为[xjyjθj]T。无人车的输入是其线速度和角速度,即[viωi](i=1,2,…)。以其中两辆车为例,领航-跟随的编队关系如图3所示。
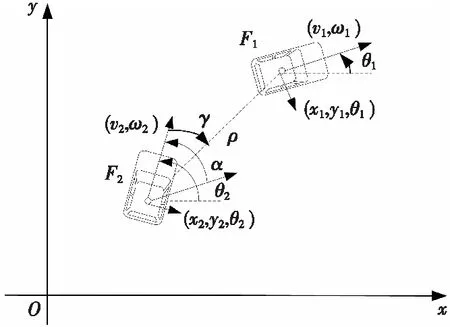
图3 领航-跟随编队坐标关系Fig.3 Coordinate relationship of leader-follower formation
根据图3,ρ为领航者质心到跟随者质心之间的距离,利用欧式距离来计算:
(2)
α为领航者和跟随者方向角差值,α=|θ1-θ2|。β为跟随者y轴到领航无人车质心的视角,β=360°-γ,令ε=β+α,则领航-跟随编队运动系统模型为
(3)

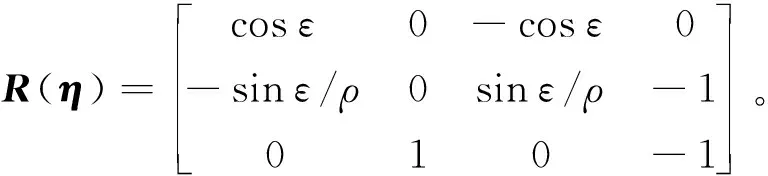
(4)
1.3 编队变换控制调节
跟随者自主导航避障之后,继续变换编队控制,使用比例-积分方式调节方向和角度偏差,进而快速恢复队形。其角速度、线速度计算公式为
(5)
(6)
式中,(dxdy)为自定义跟随者和领航者保持的x和y方向的距离,kx、kz为调节变量。
2 Lattice运动规划算法
针对Lattice规划算法全局路径拟合计算量大的问题,提出将矢量地图法融合进Lattice算法中,并且优化车辆的碰撞形状,将车辆矩形的碰撞形状近似成一组半径相同的圆,进而改进Lattice算法的代价函数。改进Lattice算法在进行采样轨迹规划时,需要将笛卡尔坐标系和Frenet[15]坐标系相互转化,以降低轨迹拟合的计算量[16]。
2.1 Lattice算法分析
Lattice规划算法,主要由状态采样、轨迹生成、碰撞检测和评价函数组成。
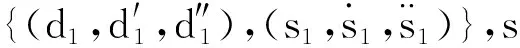
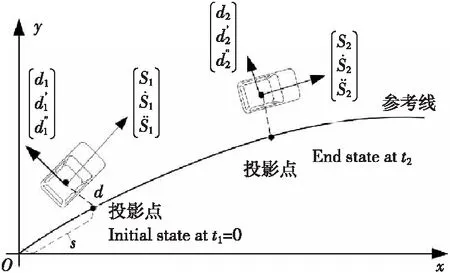
图4 基于Frenet坐标的状态采样Fig.4 State sampling based on Frenet coordinates
2)将t1起始状态、t2末状态作多项式拟合,纵向拟合多项式函数s(t)、横向拟合五次多项式函数d(s)为
s(t)=c1t5+c2t4+c3t3+c4t2+c5t+c6,
(7)
d(s)=k1s5+k2s4+k3s3+k4s2+k5s+k6。
(8)
3)将拟合横向和纵向轨迹进行合成,计算t*时刻的纵向偏移量s*=s(t*)和横向偏移量d*=d(s*),再通过全局参考线还原一个二维平面内的轨迹点Pt*=(x*y*t*)T,Pt*从t*获得一系列的轨迹点P1,P2,P3,…,最终形成一系列完整的轨迹[4]。
2.2 Lattice算法改进
Lattice规划算法需要有一条粗略的全局路径作为先验信息,但是并不要求参考路径是无碰撞的或曲率连续的,为了平滑地跟踪参考路径,并对周围环境的实时感知进行响应,提出一种改进的Lattice算法。
2.2.1Lattice全局轨迹的改进
Lattice算法中首先将车辆的初始状态和末状态转换至Frenet坐标下,然后通过五次多项式拟合形成横向轨迹和纵向轨迹,最后进行二维合成形成全局轨迹。但是对于延伸数公里的结构化道路地图,使用多项式拟合法生成全局轨迹,计算量将会成指数增长。本文提出使用输入矢量图的方法,使用矢量图可以更轻松快速地进行全局轨迹输出,其流程图如图5所示。矢量映射组件如表1所示。
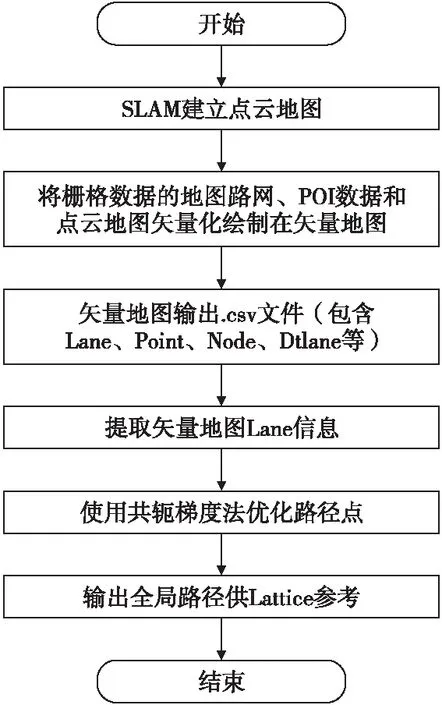
图5 生成全局轨迹流程图Fig.5 Generate global trajectory flow chart
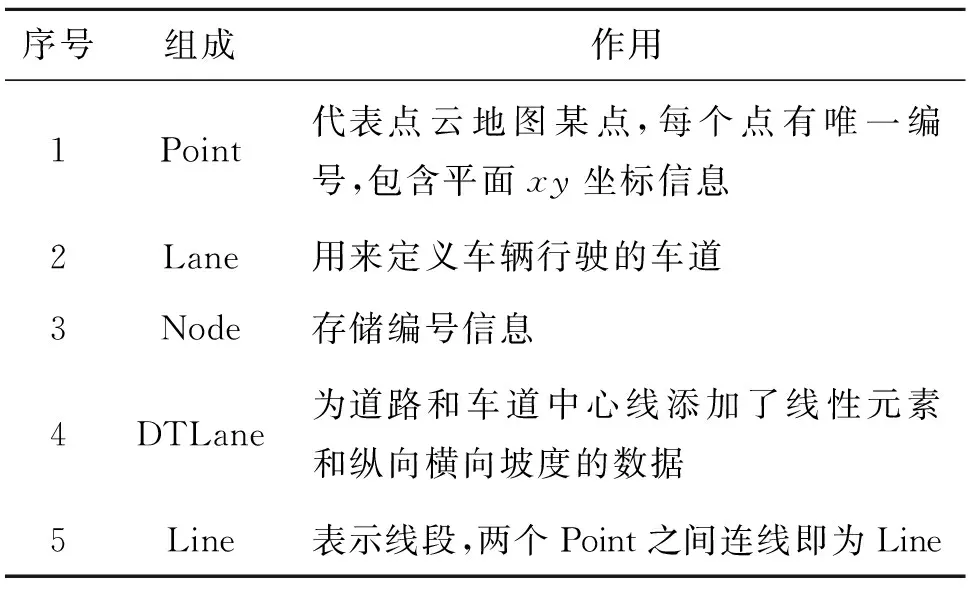
表1 矢量地图元素信息Tab.1 Element information of vector map
2.2.2Lattice碰撞策略和评价函数改进
碰撞测试采用环境感知信息进行,可以表示为占用网格图。为了降低碰撞测试的计算复杂度,本文将车辆的矩形形状改用一组半径相同的圆来近似。如图6所示,为保证安全,障碍物与圆中心之间的所有距离都必须大于圆半径。
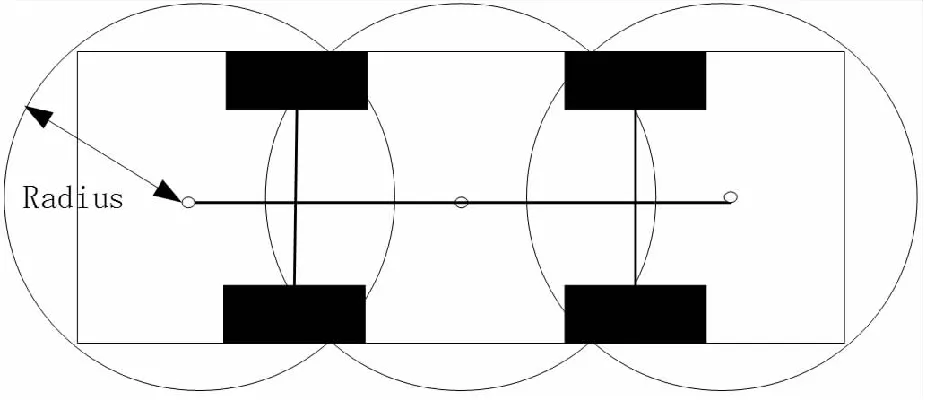
图6 车辆形状圆形分解Fig.6 Circular decomposition of vehicle shape
在此车辆形状的基础上对Lattice设置如下5个评价函数,并对每个评价函数设置权重:
1)障碍物横向距离ρa,计算障碍物各轮廓点到各轨迹的垂直距离ρa作为障碍物横向距离代价因子,障碍物与轨迹重合则设置最大值;
2)障碍物纵向距离ρc,计算车辆沿每一条备选路径方向上距障碍物轮廓点的纵向距离ρc,障碍物不在备选路径上则设置为0;
3)车辆横向偏移ρo,车辆距离中心轨迹的距离ρo,设置此代价因子主要是为了让车辆尽可能遵循全局轨迹行驶;
4)横向加速度ρm,此代价函数为了车辆平稳地变道,ρm值越小,变道越稳定;
5)向心加速度ρn,为了保证车辆能在转弯或掉头处减速慢行。在弯道处车速慢的轨迹其向心加速度就会相对较低,更容易被选出来。
最终评价函数总表达式为
(9)
式(9)中,Ci表示每一条候选路径计算出的评价值(i=1,2,3,…),λ{a,c,o,m,n}代表权重系数,ρ{a,c,o,m,n}代表各项评价函数,i是候选轨迹索引,εi是被评估的每条候选者轨迹,最终选择最小评价值轨迹。
2.2.3改进Lattice算法流程
改进的整体算法流程图如图7所示。首先通过环境感知信息获取车辆的初始状态,给定车辆一个目标点,使用矢量地图法输出全局参考路径,然后截取车体全局路径的部分距离做状态采样,将车辆目前行驶状态和截取部分路径末状态做多项式拟合,形成横向和纵向轨迹,接着给定t*时刻计算横向和纵向偏移量,再通过矢量地图法输出的全局参考轨迹还原成二维平面的轨迹点,最终形成多个完整的局部轨迹。通过碰撞测试和设定的评价函数计算每条候选轨迹的评价值,选择评价最低的作为最优轨迹。
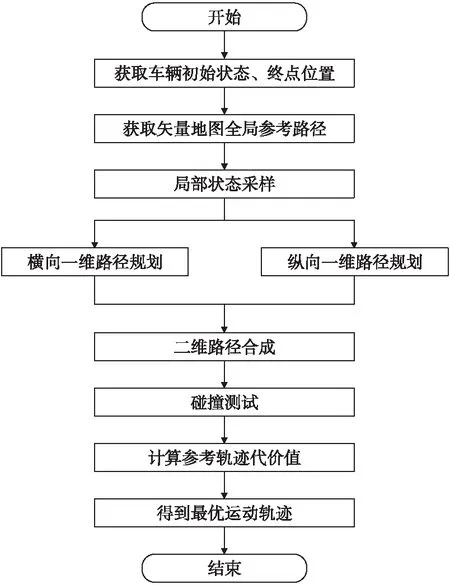
图7 整体改进算法流程图Fig.7 Overall improved algorithm flow chart
3 实验验证
对改进Lattice算法在C++环境下进行实验,为了评估改进方法,有效验证算法的真实性,本文采用Gazebo仿真环境。
3.1 改进Lattice算法全局规划实验
在此针对改进Lattice算法全局规划进行仿真,使用式(1)中无人车运动模型,约束无人车转向角度|φmax|= 0.8 rad,角速度|ωmax|=0.8 rad/s,约束线速度vmax=8 m/s,加速度|u2max|=4 m/s2,设置车辆的初始位置为(25,10),给定的终点为(32,65)。为了验证矢量地图法输出的全局路径是否符合车辆的运动学模型,在实验中构建S型弯道的全局路径。图8为在Gazebo仿真环境中建立的环境模型下,矢量地图法输出的全局路径与无人车运动模型行驶轨迹对比。矢量地图输入的S型全局路径,在路径上没有障碍物时,车辆基本按照全局路径行驶,图中输入的全局路径和车辆行驶的轨迹路线基本一致。在非完整性约束下,从图9、图10两图可看出无人车行驶的线速度、角速度v≤vmax=8 m/s,|ω|≤ωmax=0.8 rad/s,均满足运动学要求。因此矢量地图法输入的全局路径符合车辆的运动学模型。

图8 全局路径规划与车辆行驶轨迹对比图Fig.8 Comparison of global path planning and vehicle trajectory
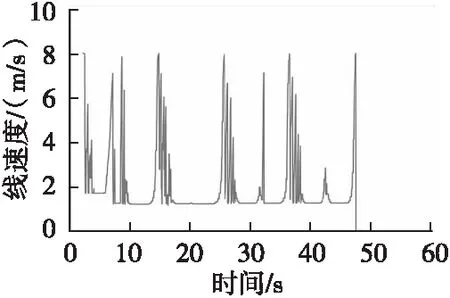
图9 车辆S弯无障碍物线速度Fig.9 Vehicle S-bend line speed without obstacles
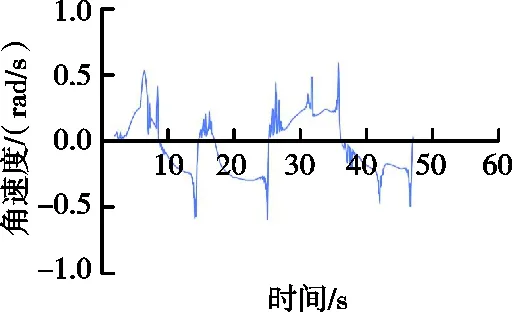
图10 车辆S弯无障碍物角速度Fig.10 Vehicle S-bending angular velocity without obstacles
3.2 改进Lattice算法局部避障实验
本节对Lattice算法的局部规划改进进行仿真,在Gazebo仿真环境中对矢量地图法生成的全局路径上添加障碍物,测试改进前与改进后的轨迹生成,轨迹图如图11所示。在实验中对线速度、转向角度、控制变量进行约束,令vmax=6 m/s,φmax=0.8 rad, |u1max|=4 m/s2,u2max=0.6 rad/s。由图11 可知,在车辆行驶路线上未遇到障碍物时,两种算法生成的轨迹几乎重合,在拐弯之后感知到前方有树时,两种算法开始规划不同的轨迹,左边轨迹为改进Lattice算法生成的轨迹,中间轨迹为Lattice算法生成的轨迹,两者均达到规避障碍物的效果。在规避障碍物时由于改进的Lattice算法将车辆形状分解成多个圆形,从而对候选轨迹的评价值计算更为灵活,避障效果更加安全。图12、图13为改进前后线速度和角速度对比。
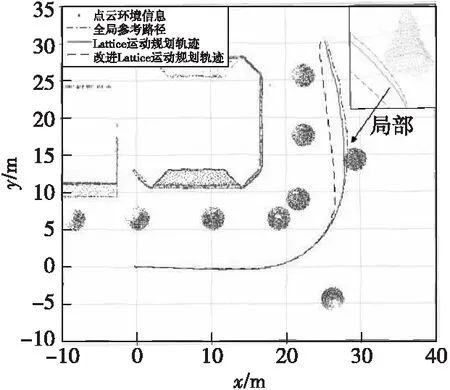
图11 算法改进前后轨迹对比Fig.11 Trajectory comparison before and after algorithm improvement

图12 算法改进前后线速度对比Fig.12 Linear velocity comparison before and after algorithm improvement
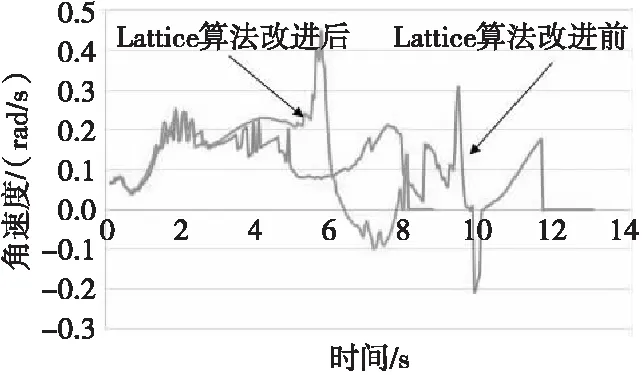
图13 算法改进前后角速度对比Fig.13 Comparison of angular velocity before and after algorithm improvement
根据对改进前和改进后的车辆线速度、角速度分析,改进后的Lattice算法不仅能够灵活规避障碍物,而且因为改进的评价函数所计算出的避障轨迹距障碍物横向距离更大,所以在行驶过程中降低对速度的控制,从而缩短车辆行驶的时间。
3.3 多车编队避障仿真实验
对编队三角阵型加入非完整性约束(车辆位置、速度和转角约束),令领航者和跟随者纵向距离保持5 m,横向距离保持5 m,将基于改进的Lattice算法应用到多车编队中。领航者和跟随者的位置通过NDT正态变换对点云地图进行匹配,可获得每台车在点云地图中的位置。设定领航者的初始位置为(28,10),跟随者1的初始位置为(33,7),跟随者2的初始位置为(23,7),对速度、转向角度、控制变量进行约束,令vmax=6 m/s,φmax=0.8 rad,|u1max|=4 m/s2,|u2max|=0.6 rad/s,实验结果如图14所示。编队模型中各车线速度和角速度如图15、图16所示。
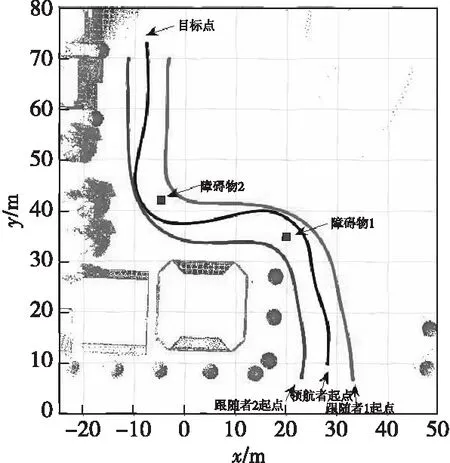
图14 多车编队及避障轨迹图Fig.14 Multi-vehicle formation and obstacle avoidance trajectory diagram
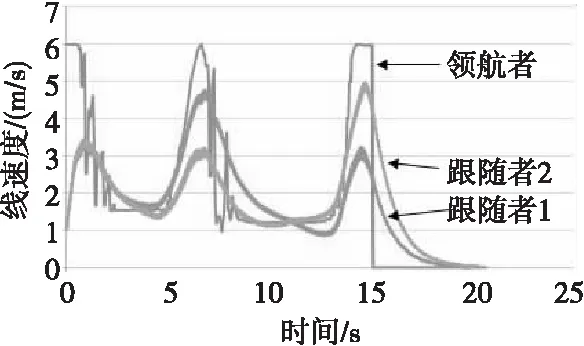
图15 编队模型中各车线速度Fig.15 Line speed in formation model
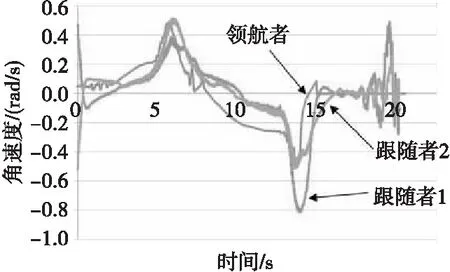
图16 编队模型中各车角速度Fig.16 Vehicle angular velocity in formation model
根据图14可看出在编队运动过程中,不仅能保持编队队形行驶,而且在行驶路径上遇到障碍物时能够动态规避障碍物。根据图15、图16可看出领航者前行时,跟随者线速度和角速度通过多车模型实时调节,使其一直保持指定三角阵型行驶。
4 结论
本文提出将改进Lattice算法应用到多无人车编队运动规划中,该算法可在结构化道路环境下简化领航者全局轨迹生成的复杂度,并提高车辆局部避障的精确性;另外在编队运动过程中加入车轮转向角度、角速度等非完整性约束以及跟随者自主导航行为,设计队形恢复调节函数,使各车能够分布式避障后快速恢复队形。仿真实验证明,基于改进Lattice算法的多无人车编队在按照规划的全局轨迹行驶时,能够根据周围环境信息灵活避障和队形保持。
