基于多通道探测的场向不均匀体定位方法
2022-11-04唐志坤龚晚林
唐志坤,龚晚林
(武汉大学电子信息学院,湖北 武汉 430072)
0 引言
甚高频(very high frequency, VHF)雷达是对场向不均匀体进行探测研究的常用探测设备,利用场向不均匀体的后向散射特性,测量场向不均匀体的距离与多普勒速度,在全球范围被广泛应用,包括印度Gadanki VHF雷达,秘鲁Piura VHF雷达,日本与印度尼西亚共同建造的MU VHF雷达,以及中国三亚VHF雷达、富克VHF雷达与台湾中坜VHF雷达。但在VHF雷达对场向不均匀体的探测中存在着以下缺陷:在单波束模式中只能得到距离-时间-强度(range-time-intensity, RTI)图以及多普勒速度,无法从RTI图中获取电离层场向不均匀体的空间结构,并且由于VHF雷达存在旁瓣过高问题,信号从旁瓣接收导致雷达系统对于信号实际来波方向误判,无法确定不均匀体在空间中的位置。针对这些问题,通过对雷达升级改造使其具有多通道探测能力,基于多通道探测数据,利用空间干涉法得到场向不均匀体的空间中位置。
空间干涉法是研究场向不均匀体的重要方法,通过多个通道接收场向不均匀体的回波信号,通过不同通道间的相位差计算出场向不均匀体在空间中的位置与形态。由D.T. Farley于1981年最先运用在Jicamarca雷达上,用于研究电离层等离子体扰动过程[1],Jicamarca雷达从原有的单通道接收信号升级到双通道接收信号,可以确定在波束范围内的场向不均匀体在东西平面上的位置。随后在1991年由CUPRI改进,提高至三通道接收信号[2],实现在三维空间中的获取场向不均匀体的位置,用于研究E层与F层场向不均匀体的空间细节。之后空间干涉法被广泛应用于多部VHF雷达上,如中坜VHF雷达[3]、三亚VHF雷达[4]等。富克VHF雷达进行了相应的升级改造,在原阵列的北侧新建两个子阵列,用于接收回波信号,实现多通道探测。本文利用富克VHF雷达三通道探测数据实现对场向不均匀体三维空间定位,且增加相位解模糊过程,对主瓣回波与旁瓣回波均能实现空间定位,并利用该方法对富克VHF雷达探测到的典型回波案例的空间结构进行了相关研究。
1 场向不均匀体探测原理
场向不均匀体是电离层中电子密度高于或低于其他介质电子密度的部分。无线电波经过场向不均匀体会导致其产生快速且剧烈的变化,对无线电通信产生严重影响,因此对于场向不均匀体的探测研究有重要意义。
VHF雷达是常用的对场向不均匀体的探测设备,雷达发射的VHF波段的信号与场向不均匀体的散射回波产生相干叠加,并由雷达天线接收到信号,得到场向不均匀体的距离与多普勒速度信息。多通道探测利用多个天线阵列独立进行接收信号,得到空间中不同位置的回波的相位信息,利用相位差计算出回波的方向。图1为测向原理图,天线i与天线j为两个天线接收单元,dij为天线i指向天线j的向量,ΔLij为两个天线接收信号的波程差,两天线接收信号的相位差为
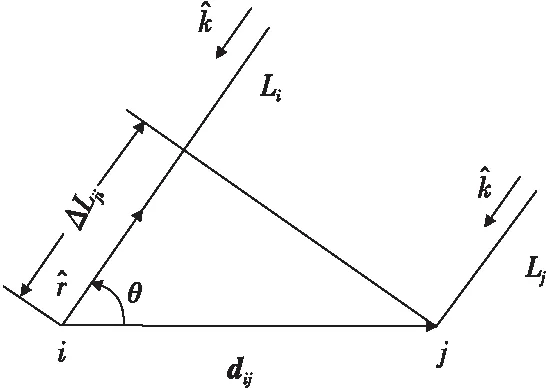
图1 测向原理图Fig.1 Diagram interferometric direction finding
(1)
由式(1)可以得到回波方向与相位差的关系为
(2)
通过多通道探测得到回波的方向后,结合单通道探测中得到的回波距离,实现对场向不均匀体的空间定位。
2 多通道VHF雷达空间定位方法
2.1 探测设备介绍
升级改造后的富克VHF雷达在原有基础上添加了两个新阵列,两个新阵列仅用于接收回波,表1给出了富克VHF雷达的发射参数[5]。
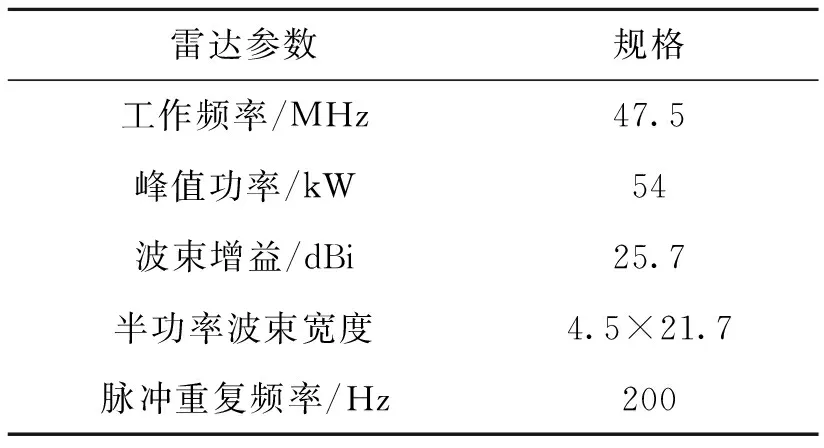
表1 雷达系统参数Tab.1 Radar system parameter
子阵列1由18×4五单元八木天线组成,子阵列2、子阵列3均由9×4五单元八木天线组成,阵列间的位置关系如图2所示。
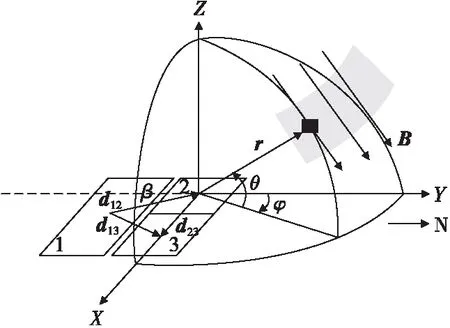
图2 雷达天线阵列图Fig.2 Antenna array diagram of radar
数据处理流程均在CPU为i7-9400F,内存16 G的硬件平台上,操作系统为Windows 10,使用Matlab R2021版本软件环境进行数据处理。
2.2 互相关叠加
将三通道回波信号分别进行FFT与非相干叠加,得到信号归一化互相关谱, 式(3)中〈〉运算符表示非相干叠加与平均运算。
(3)
根据式(4)可以通过归一化互相关谱计算出回波信号之间的相位差:
S21(ω)=〈eiΔφ〉。
(4)
当归一化互相关谱模值大于阈值0.7时,认为回波来自于同一散射区域。通过式(5)得到天线阵列1与天线阵列2的相位差:
(5)
式(5)中,imag(S21(ω)),real(S21(ω))分别为S21(ω)的虚部与实部。
图3给出了2020年4月5日当地时间19:44时刻,在距离为106.8 km的回波互相关谱与相位差。在互相关谱图中加粗的点为互相关谱模值大于0.7的点以及对应的相位差。通过选取互相关谱模值大于0.7的点,得到不同通道间的相位差。
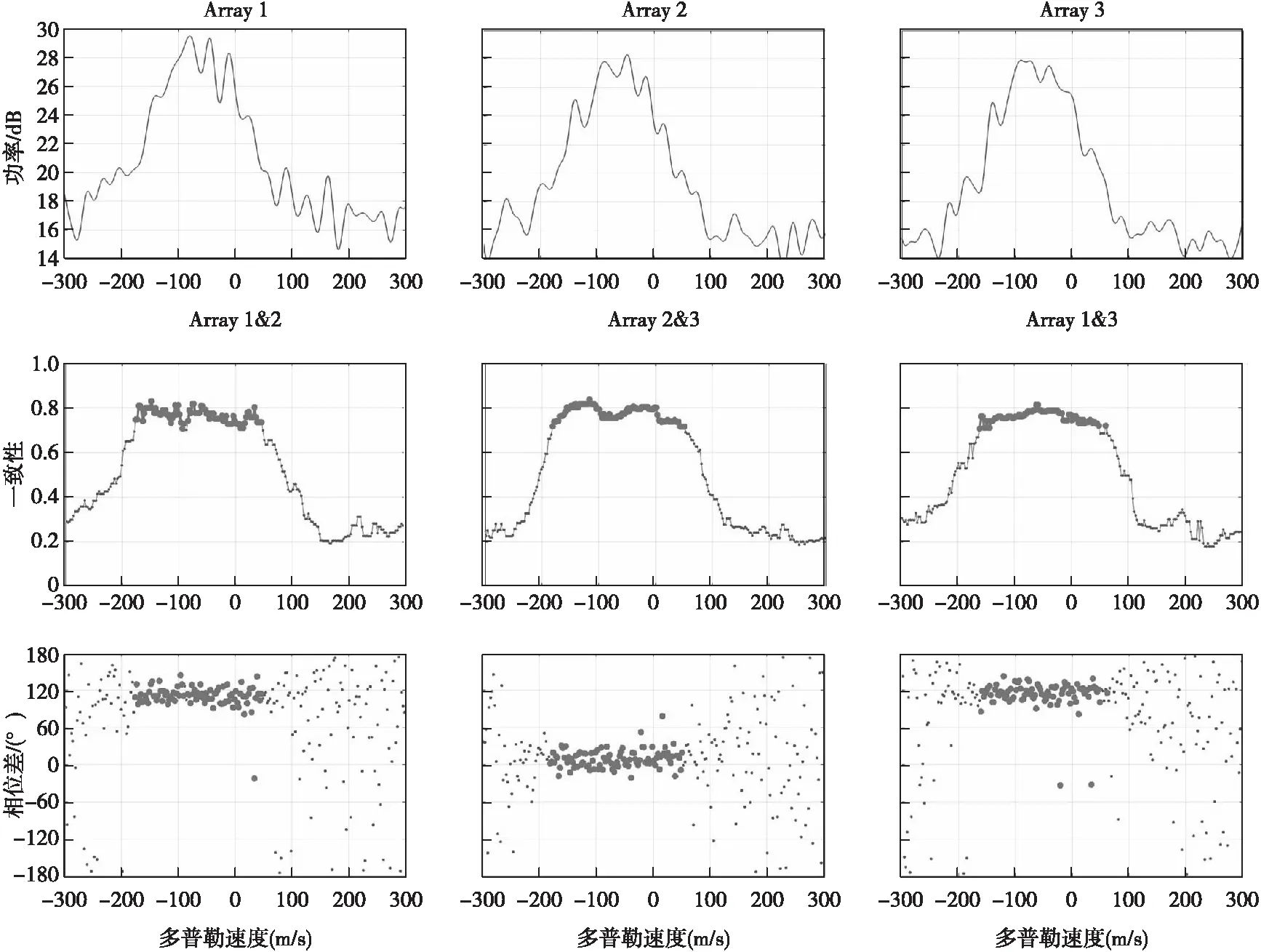
图3 当地时间2020年4月5日19:44,距离为106.8 km回波信号的互相关谱与相位差Fig.3 Cross-spectra and phase difference at range 106.8 km on 05 April 2020, 19:44LT
2.3 相位解模糊
在实际探测中,测量相位差为实际相位差对360°取模后的值。因此我们需要通过将测量相位差增加特定的整数倍360°,使测量相位差恢复到实际相位差。
天线阵列接收信号之间的测量相位差与实际相位差的关系:
Δφ21,actual=Δφ21,measure+l·360°,
(6)
Δφ32,actual=Δφ32,measure+m·360°,
(7)
式(6)、(7)中,l与m称为干涉波瓣数[6],需要确定l与m的值将测量相位差恢复到实际相位差。
当波束与场向不均匀体近似垂直时才能接收到回波。场向不均匀体在空间中的分布满足沿地磁场分布,通过国际地磁参考场(international geomagnetic reference field, IGRF)模型统计所有场向不均匀体可能的分布,得到预测回波区域。通过调整干涉波瓣数l与m的值,使实际相位差在预测相位差范围内,得到实际相位差。
图4为2020年5月15日当地时间00:21:59时刻回波相位差,图4(a)为测量相位差,图4(b)为进行解模糊后得到的实际相位差。图中黑色区域为预测相位差范围,根据不同的相位差使用不同的干涉波瓣数l与m,得到的实际相位差如图4(b)所示,大部分回波的实际相位差在预测相位差范围内。相位解模糊过程有效地将测量相位差恢复到实际相位差。
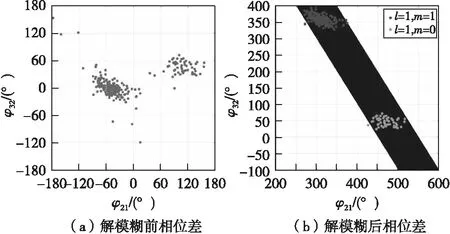
图4 相位解模糊前后相位差对比Fig.4 Comparison of phase difference before and after unwrapping phase ambiguity
2.4 初始相位差校正
通常来说,雷达系统都会存在一个固有相位差,去除固有相位差才能确定正确的相位差。通过找到一个已知位置的目标实现对初始相位差带来的误差进行校正,是常用的校正雷达系统固有相位差方法。
由于Es层场向特性以及Es层的空间分布相当窄的特性,Es层可以作为已知位置的目标[7]。选取2020年5月13日21:25至22:00时间内Es层回波数据,记录下所有满足条件的Δφ21和Δφ32。
当波束方向与地磁场近似垂直时可以接收到Es层回波[8]。通过IGRF模型获取地磁场模型,记录高度范围在90~125 km内满足波束方向与磁场的垂直方向夹角小于0.5°区域的仰角与方位角。利用方位角仰角与相位差的关系得到Es层回波的预测相位差。通过移动测量相位差Δφ32,predict和Δφ21,predict,使得测量相位差全部在预测相位差区域内。预测相位差、校正后相位差与测量的关系如图5所示。雷达系统的固有相位差为
Δφ21,bias=22°,Δφ32,bias=0°。
(8)
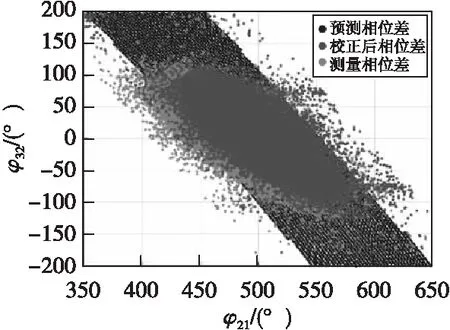
图5 天线阵列初始相位差校正Fig.5 Calibration of initial antenna array phase bias
2.5 计算回波区域在空间中的位置
经过相位解模糊与初始相位差校正后,得到实际相位差,利用实际相位差与雷达天线阵列的位置关系,可以得到回波的方位角与仰角。波程差与回波的方位角φ,仰角θ的关系满足:
Δλ32=d32cosθsinφ,
(9)
Δλ21=d21cosθcos(φ+θ)。
(10)
联立式(9)、式(10)得到回波区域的方位角φ、仰角θ与相位差Δφ21、Δφ32的关系:
(11)
(12)
回波区域分布范围较小,在计算回波区域位置时,可以近似在直角坐标系下计算,得到回波区域在直角坐标系下的坐标:
xEW=rcosθsinφ,
(13)
yNS=rcosθcosφ,
(14)
(15)
式中,Re为地球半径,xEW、yNS分别为在以雷达为原点的直角坐标系下x轴与y轴的坐标,h为在地心为球心的球坐标系下回波区域相对地面的高度。
3 实测结果与分析
3.1 主瓣与旁瓣回波区分
图6为2020年5月15日00:21:59时刻,利用富克VHF雷达多通道探测数据得到的电离层场向不均匀体的三维空间结构投影图。
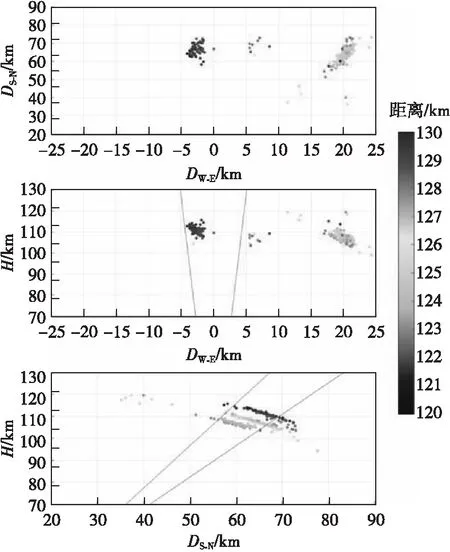
图6 当地时间2020年5月15日00:21:59探测到的场向不均匀体的空间结构Fig.6 Spatial structure of field aligned irregularities on 05 May 2020, 00:21:59LT
回波区域分为东西向分布在-5~0 km的主瓣回波区域与东西向分布在17~22 km的旁瓣回波区域。通过相位解模糊有效地区分了主瓣回波与旁瓣回波,且对于主瓣回波区域与旁瓣回波区域,均在预测回波区域内,满足VHF雷达基于布拉格散射原理的特性,通过相位解模糊,有效地实现了对主瓣回波区域与旁瓣回波区域的定位。
3.2 准周期回波
准周期(quasi-periodic, QP)回波是E层常见回波,对于QP回波的空间结构存在着不同的解释:文献[9]提出的在Es层中存在着高电子密度的连续场向不均匀体,对应着RTI图中高强度回波;文献[10]提出了剪切不稳定性造成的涡旋结构[10],许多小的漩涡结构场向不均匀体进入雷达视场,形成RTI图中QP回波。
图7为富克VHF雷达在2020年04月05日20:00至20:30时间内探测到的典型夜间QP回波的RTI图。在RTI图中,QP回波距离分布在106~110 km,呈现出明显的负向QP回波特性,距离随时间下降,呈负向倾斜,周期约为2 min。

图7 当地时间2020年04月05日探测到的QP回波RTI图Fig.7 Range-time-intensity plot of QP echo on 05 April 2020LT
图8为20:11:15至20:14:45时间内场向不均匀体的三维空间结构投影图。在图中可以得到场向不均匀体的高度分布在90~98 km,在东西方向上分布在-3~3 km,沿场向排列。在这两个QP回波周期内,场向不均匀体运动特性相同,均从较高高度进入雷达视场,高度逐渐下降,在东西方向上自西向东运动,直至离开视场,与RTI图中向下倾斜的条纹状回波对应。从QP回波的三维结构中可以看到QP回波是由较小的场向不均匀体从西侧较高的高度进入雷达视场,场向不均匀体向下与向东方向漂移出雷达视场。观测结果符合文献[10]提出的剪切不稳定性产生的许多小的涡旋结构形成RTI图中的QP回波。
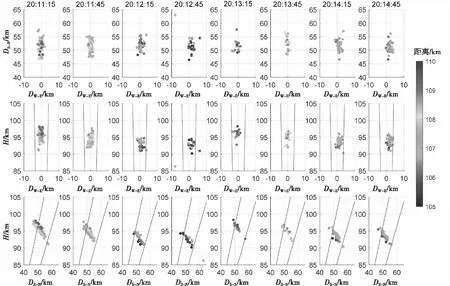
图8 当地时间2020年04月05日探测到的QP回波的三维空间结构投影图Fig.8 Three-dimension spatial structure of QP echo projection plot on 05 April 2020LT
3.3 V型回波
在2013年至2015年,富克VHF雷达多次观测到特殊的V型回波[11],出现在100~180 km范围内,在较高的高度进入雷达视场,初始时强度较弱,随着距离下降回波强度增强,到达距离最低后距离又逐渐上升,回波强度也随之减弱。V型回波被认为是雷达的旁瓣回波,是由E层不均匀体东向或西向运动形成的RTI图上距离增加的V型回波。图9为2020年5月15日00:20至00:45时间内的回波RTI图,在RTI图中可以看到回波在距离较低处强度较高,随着回波的距离逐渐上升强度也逐渐减弱,呈现出与V型回波类似的图案。
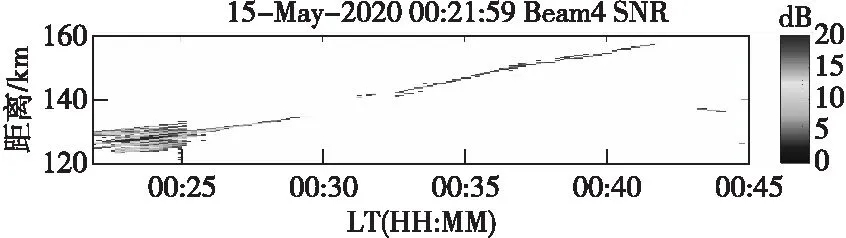
图9 当地时间2020年05月15日探测到的V型回波RTI图Fig.9 Range-time-intensity plot of V-shaped echo on 15 May 2020LT
图10为00:34:59至00:40:59时间内的回波区域三维空间结构投影图,从图中可以看到在东西方向上,场向不均匀体出现在30~40 km,回波在东向运动的过程,在距离快速增加的过程中,高度始终维持在125~135 km,由此可以证明在RTI图中,V型回波是由于场向不均匀体东向或西向的运动产生的。场向不均匀体从西侧的旁瓣进入雷达视场,向东运动靠近雷达。进入主瓣后,由于主瓣波束增益远大于旁瓣回波,因此在RTI图中回波强度增强,随后继续向东运动远离雷达,离开主瓣后,回波强度减弱。观测结果与V型回波由场向不均匀体东向或西向产生的说法相符合。
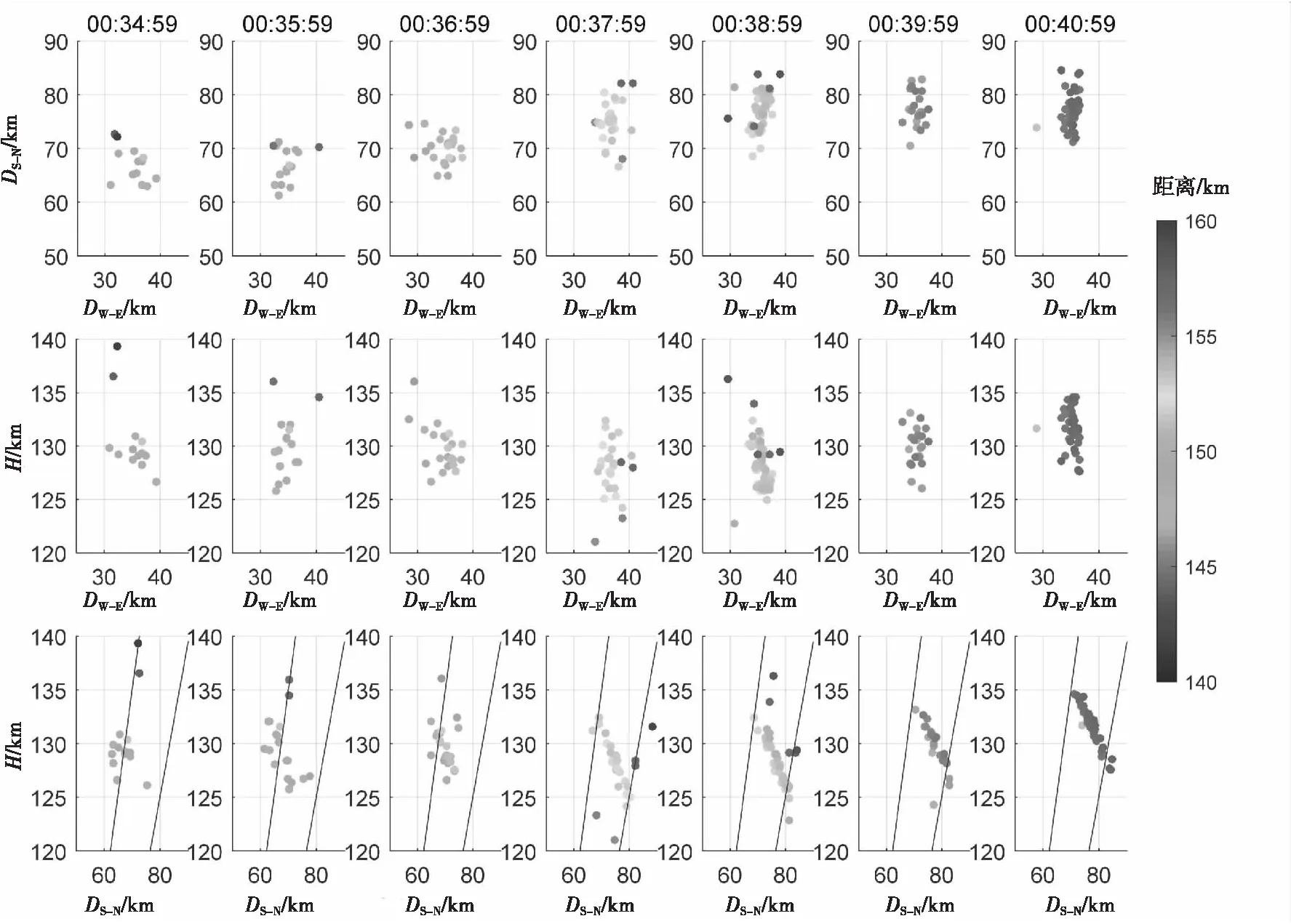
图10 当地时间2020年05月15日探测到的V型回波三维结构投影图Fig.10 Three-dimension spatial structure of V-shaped echo projection plot on 05 May 2020LT
4 结论
本文基于富克VHF雷达多通道信号,实现了对场向不均匀体的空间定位。相较于原有单通道接收信号,新增了对于场向不均匀体精确位置以及实际运动方向的观测能力,并新增了相位解模糊过程。探测结果表明,通过新增相位解模糊过程后,空间干涉法对于来自主瓣回波与旁瓣回波能够区分,且均能实现对场向不均匀体的正确定位。利用该方法对两种常见的场向不均匀体回波,QP回波与V型回波的形态与运动趋势进行了相关研究,均与现有的物理机制相符合,该方法对于利用VHF雷达对场向不均匀体的研究有重要帮助。
