PROBING A STOCHASTIC EPIDEMIC HEPATITIS C VIRUS MODEL WITH A CHRONICALLY INFECTED TREATED POPULATION*

S.P.RAJASEKAR M.PITCHAIMANI

1.Ramanujan Institute for Advanced Study in Mathematics,University of Madras,Chennai -600 005,Tamil Nadu,India;

2.Department of Mathematics,Government Arts College for Women,Nilakottai -624 202,Tamil Nadu,India

E-mail: sekaraja.sp@gmail.com;mpitchaimani@yahoo.com

Quanxin ZHU (朱全新)†

CHP-LCOCS,School of Mathematics and Statistics,Hunan Normal University,Changsha 410081,China

E-mail: zqx22@126.com

Abstract The hepatitis C virus is hitherto a tremendous threat to human beings,but many researchers have analyzed mathematical models for hepatitis C virus transmission dynamics only in the deterministic case.Stochasticity plays an immense role in pathology and epidemiology.Hence,the main theme of this article is to investigate a stochastic epidemic hepatitis C virus model with five states of epidemiological classification: susceptible,acutely infected,chronically infected,recovered or removed and chronically infected,and treated.The stochastic hepatitis C virus model in epidemiology is established based on the environmental influence on individuals,is manifested by stochastic perturbations,and is proportional to each state.We assert that the stochastic HCV model has a unique global positive solution and attains sufficient conditions for the extinction of the hepatotropic RNA virus.Furthermore,by constructing a suitable Lyapunov function,we obtain sufficient conditions for the existence of an ergodic stationary distribution of the solutions to the stochastic HCV model.Moreover,this article confirms that using numerical simulations,the six parameters of the stochastic HCV model can have a high impact over the disease transmission dynamics,specifically the disease transmission rate,the rate of chronically infected population,the rate of progression to chronic infection,the treatment failure rate of chronically infected population,the recovery rate from chronic infection and the treatment rate of the chronically infected population.Eventually,numerical simulations validate the effectiveness of our theoreticalconclusions.

Key words hepatitis C virus;acute and chronically infected;chronically infected treated;extinction;stationary distribution

1 Introduction

The hepatitis C (HCV) virus is a hepatotropic RNA virus that accelerates liver fibrosis,cirrhosis and causes hepatocellular carcinoma (HCC),and is a major threat for liver cancer related mortality worldwide among the human population [1].Flaviviridae is a family of single positive stranded RNA viruses,which contains three genera: flaviviruses,pestiviruses and hepaciviruses [1,2,7,9,10].HCV is a blood-borne virus that induces both acute and chronic infection,and which can lead to chronic liver disease.HCV infection is chiefly transmitted by the transfusion of contaminated blood or blood products;this can occur with contaminated needles/syringes,unsafe injection practice,skin-piercing mechanisms and through injecting drug use (IDU) [3].Heavy alcohol ingestion (as opposed to social drinking) remains a pivotal risk factor for the growth of HCC [3,4,7,8].Exposure to blood during sex may amplify the possibility of HCV [11,12].Generally,HCV infected individuals are asymptomatic until two weeks to six months after transmission (incubation period) [2].No effective prophylactic vaccine against HCV has yet been found,though research by medical scientists continues [6].

After the incubation period of HCV RNA virus within the blood,the acute HCV infection develops as chronic hepatitis C,which is generally sub-clinical [3].At this stage of acute infection,nearly 80% of infected individuals do not exhibit symptoms [5],though certain symptoms can be determined in a minority of acute infected individuals: fatigue,loss of appetite,fever,nausea,vomiting,abdominal discomfort,anorexia,dark-urine and jaundice.Untreated,60-80% of acute HCV individuals may eventually progress to chronic HCV infection.Most chronic HCV sufferers are asymptomatic until potential complications such as cirrhosis,liver damage,liver failure and liver cancer evolve [1,5,13].The Center for Disease Control and Prevention(CDC) reports that approximately 10-20% of people with chronic untreated HCV ultimately wind up with liver cirrhosis,which can cause complications like jaundice,ascites,the need for a liver transplant,hepatic encephalopathy,swelling in the ankles/feet,bleeding from esophageal varices and death [1–4,8,10].

The HCV viral genome is a single-stranded RNA with a positive polarity of nearly 10,000 nucleotides;it is packed with a core protein and enveloped in a lipid bi-layer in which two envelope glycoproteins (E1 and E2) frame the HCV virions.It is spherical and about 45-65 nm in diameter [1,2,9].The HCV genomic RNA has a long open reading frame (ORF) of about 9,000 nucleotides;the ORF produces a polyprotein of nearly 3,000 amino acids.The ORF is flanked by 5′and 3′untranslated regions (UTR) vital for viral translation and replication [2,10].The three structural proteins,like the core and envelope glycoproteins E1 and E2,include those related to viral particle production.There are seven nonstructural proteins including p7,NS2,NS3,NS4A,NS4B,NS5A and NS5B;these allow viral processing and replication,along with particle assembly [1,10].The host of low-density lipoproteins (LDLs) and verylow-density lipoproteins (VLDLs) are known as lipoviroparticles,and they are associated with HCV virions.Lipoviroparticles contain Apolipoprotein B (APOB),APOC,and APOE also.Low ailing infectious non-enveloped viral capsids may persist in the blood of infected individuals[1].

HCV is a high genetic heterogeneous virus.Phylogentic analysis of HCV has revealed 7 main genotypes in different regions of the world that vary in their nucleotide level by 30%,and a large number of subtypes that vary in their nucleotide level by 15-25% [1].Subtypes of the genotypes are labeled as 1a,1b and so on.A global survey carried out recently discovered the genotypes 1 and 3 are the most rampant,claiming up to 46% and 30% of all infections,respectively;genotypes 2,4,5 and 6 accounted for 9%,8%,1% and 6%,respectively [7–10].Genotype 7 has been identified in only a very few individuals from Central Africa [18].Across Europe,about 90% of all cases are genotypes 1,2 and 3;genotypes 1 and 3 have a conspicuous presence in most European countries,though genotype 2 is mostly present in Italy;genotypes 4 and 5 have an escalating presence,but genotype 6 is scarcely seen.In many of the American countries the majority of infections are genotype 1 (1a and 1b);the rest are genotypes 2 (particularly 2a) and 3a.Genotype 3 is discovered rarely in Africa;here genotypes 1,2 and 4 are the most rampant in North and Central Africa,genotypes 1 and 5 dominate South Africa,and genotypes 4 and 5 are the most rampant in North East and Central Africa.A great part of infections in the Indian subcontinent and Thailand are of genotype 3,including innumerable subtypes as originally confirmed in samples from Nepal.Genotype 6 is discovered in 10-20% of the population in many regions of East and South East Asia with a high presence of subtype 6a.To sum up,genotype 1 (1a and 1b) is the most rampant,followed by subtype 3a,which is found primarily in Russia and Australia/New Zealand [7–10,18].

Pretreatment analyses required for anti-HCV treatment can consist of interferon (INF),determination of HCV genotype,determining the present status of the disease (acute,chronic),assessing the stage of liver disease (fibrosis,cirrhosis),considerations of alcohol addiction,evaluation of the immune system,and assessment for HIV/HBV co-infection and co-morbidities[9,13].These days,combinations of direct-acting antivirals (DAAs) have widely replaced INF based therapy [13].In 1998 and 2001,INF plus ribavirin (RBV) and pegylated (Peg)-IFNs plus an RBV antiviral agent was the standard of care,but those were unable to wipe out chronic HCV infection.On the other hand,sustained virologic response (SVR,defined as no discernible HCV RNA in the blood circulation 12-24 weeks after antiviral therapy cease)achieved average cure rates of 42-45%,65-85%,and 70-80% of infected patients with HCV GT1;GT4,GT5 or GT7;and GT2 or GT3,respectively [1,7,9,13].In November 2013,NS3/4A and NS5A protease inhibitors (simeprevir) were endorsed by the Food and Drug administration (FDA) and this was followed December 2013 by another NS5B polymerase inhibitor(sofosbuvir-SOF).Combining two (simeprevir and SOF) or three DAAs provides excellent tolerability and safety for HCV patients with HCV GT1,and cure rates are 90-100% are attained[13].Combinations with SOF/ledipasvir (NS5A replication complex inhibitors) and ombitasvir(NS5A)/paritaprevir (NS3/4A protease inhibitors)/r+dasabuvir (nonnucleoside inhibitor of NS5B) were endorsed by the FDA in October and December 2014,respectively [9,13].In July 2015,SOF+daclatasvir (DCV;NS5A replication inhibitors)+RBV achieved very high SVR rates (95%) in patients with HCV GT1 with excellent tolerabilty and safety.In 2016,the FDA approved elabasvir/grazoprevir to treat chronic HCV patients in the USA and Europe,and SOF/velpatasvir (VEL;NS5A replication inhibitors) ± RBV regimens reached 50-100%in chronic HCV patients with good tolerability [1,9,13].Finally,SOF+RBV reached high SVR rates in chronic HCV patients with GT1,and furthermore,was revealed to be effective in individuals with GT4,GT5 or GT7 infection [9].

This segment focuses on HCV as a stealth virus,one that in the course of the infection attacks the command and control point of the immune system,the CD4 helper T cells,by eliminating epitopes that deregulate antiviral Type 1 cytokines like interleukin (IL)-2 and interferonγ(IFN-γ) and on-regulate Type 2 cytokines such as MHC class II molecules and chemokines,which nourish host tolerance to HCV.Infection with HCV paves the way for chronic susceptibility in 85% of patients without evidence of active,antiviral immunological responses [2,14].Knowing the means by which HCV sets and maintains infection is also to examining modes of human immunoregulation.The part played by CD4+and CD8+T cells in HCV clearance or disease pathogenesis is,at least,ambiguously understood.Certainly,the fact that infection consistently occurs despite the existence of virus-specific CD4+and CD8+T cells in the liver and the peripheral blood implies that these responses are ineffective for many patients.Both innate and adaptive immune responses are vital for HCV viral eradication.For the innate immune response,natural killer (NK) cells appear to be useful in eliminating HCV infection,and it seems that some kind of NK cell receptor genes (KIR2DL3 and HLA-C1) are related to viral eradication [1,2,14,15].

CD4 T cells can be partitioned into at least two types,T helper 1 (Th1) and T helper 2 (Th2),these have different roles in the immune response.The role of CD4 T cells which are prominent in viral escape is problematic;it is easier to handle viral escape methodologies from the point of view of the antibody or killer T-cell identification of viral epitopes.A failure to recognize the causes of viral “escape” would bring about a failure in antibody-facilitated clearance or neutralization of infected cells.HCV has developed several techniques for eluding or evading immense response.For instance,the HCV NS3/4A protein can split and neutralize two host indicating processes that react to HCV pathogen-associated molecular designs to instigate the IFN process.IFN-stimulated genes are sterilized during innate HCV infection,but this is not very effective at doing away with the virus [1,14].Rapidly increasing evidence asserts that CD4 T cells can also have a direct impact on virus-infected target cells,varying from cytotoxicity to secretion of antiviral cytokines like IFN-γand tumour necrosis factor-α(TNF-α).On one level,CD8+killer T cells are somehow required for the ultimate extinction of HCV,and killer cell differentiation rests upon Type 1 cytokines.The last that most patients are unable to recover from the disease highlights the fact that CD8 T-cell responses are neutralized.The origins of these cytokines in the liver environment may not fall in line with conventional paradigms.These somewhat paradoxical observations culminate with the observation that there do exist HCV antigens that are able to extinguish the virus from the blood and liver of at least a minor segments of patients.Here it is suggested that suitable intensive immune responses to HCV are possibly to be controlled by CD4+regulatory T cells [14,15].

Based on HCV viral pathology,reinfection plays as significant a role as primary infection,with respect to infection rate,progression rate,treatment rate and recovery rate (partial or loss of immunity).The treatment model for HCV transmission dynamics [6,17] is given by the following deterministic nonlinear differential system of equations:

Here Φ=β(I+πP+λπT).

The biological meaning of all positive parameters and variables in the deterministic HCV model (1.1) are listed in Table 1.

Table 1 Biological meaning of variables and parameters of deterministic model (1.1)

The basic reproduction number of the deterministic HCV system (1.1) is

Consequently,in [6],the deterministic HCV model (1.1) has the following properties:

· if R0≤1,the deterministic HCV system (1.1) has an infection-free equilibriumE0=(S0,I0,P0,R0,T0)=(Λμ,0,0,0,0),which is globally asymptotically stable on Γ;

· if R0＞1,the deterministic HCV system (1.1) has an endemic equilibriumE1=(S1,I1,P1,R1,T1),which is globally asymptotically stable on Γ.

The biological processes captured and expressed by mathematical models for disease transmission can be valuable in real life scenarios,but deterministic models can be influenced by environmental white noise or by the presence of uncertainty.The treatment model for HCV system (1.1) is perpetually subject to stochastic effects which occur at all levels,from susceptible to chronically treated populations.Phenomena are inevitably modeled and stochastically perturbed based on environmental white noise,and understanding this is essential for a better understanding of many biological phenomena.Stochasticity impacts upon various biological[22–30,39,40,43,44] and other models [31–36,38].Inspired by the above factors,we put forth the stochastic epidemic HCV model for a chronically treated population.The stochastic epidemic HCV model is on the basis of the influence of the environment on individuals manifested by stochastic perturbations,and it is proportional to each state [22,25,41,42].In this paper,the theoretical findings extend to the analysis of the corresponding deterministic system.

We construct the following stochastic epidemic HCV model:

Here Φ is defined in (1.1).

LetW(t)=(W1(t),W2(t),W3(t),W4(t),W5(t)) be a 5-dimensional Wiener processes defined on the given probability space.The components ofW(t) are supposed to be mutually independent.In the stochastic model (1.2),the non-negative constantsσ1,σ2,σ3,σ4andσ5reflect the intensities of the environmental white noise.

The rest of this article is organised as follows: in Section 2 we address the existence of global and unique positive solutions to stochastic HCV model (1.2).In Section 3 the sufficient conditions for the extinction of the hepatotropic RNA virus are attained.Section 4 establishes that there is a unique ergodic stationary distribution of the positive solutions of the stochastic HVC model (1.2) under some conditions.In Section 5 the five-dimensional stochastic model of a hepatitis C virus is validated by extensive numerical simulations,and the dynamics of the stochastic HCV system (1.2) are analyzed.

2 Existence of a Unique Global Positive Solution

It is first pivotal to discover whether or not the solution has global existenceS(t),I(t),P(t),R(t) andT(t) signify the portion of the population that is susceptible,acutely infected,chronically infected,recovered and chronically infected,and treated,respectively,at timet.Here the main consideration is that the solution to the stochastic HCV system (1.2) is global and positive.

Theorem 2.1The stochastic HCV system (1.2) has a unique positive solution (S(t),I(t),P(t),R(t),T(t)),with initial values (S(0),I(0),P(0),R(0),T(0)) for allt≥0;the solution will remain inR5+with probability one,namely,(S(t),I(t),P(t),R(t),T(t)) ∈R5+for allt≥0 almost surely.

ProofRegarding the stochastic HCV system (1.2),its coefficients are locally Lipschitz continuous,so for any initial values (S(0),I(0),P(0),R(0),T(0)) ∈R5+,there exists a unique maximum local solution (S(t),I(t),P(t),R(t),T(t)) ont∈[0,τ*),whereτ*is the explosion time.To show that this solution is global,we should have thatτ*=∞,almost surely (a.s.).We show that (S(t),I(t),P(t),R(t) andT(t)) do not explode to infinity in a finite time.Letν0＞1 be adequately large such thatS(0),I(0),P(0),R(0) andT(0) all lie within the intervalFor each integerν ＞ν0,define the stopping time [21] as

where throughout the entire paper,we set inf Ø=∞(Ø denotes the empty set).Obviously,τνis increasing asν→∞.Leta.s..Next,we demonstrate thatτ∞=∞,a.s..If this affirmation is false,then there is a constant＞0 and anε∈(0,1) such that

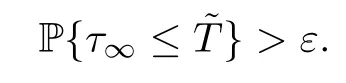
Thus there exists an integerν1≥ν0such that

whereaandbare positive constants to be resolved later.The non-negativity of theV1function can be seen from (u-1 -lnu) ≥0 for allu ＞0.

Utilizing Itˆo’s formula onV1,we have that

where C is a positive constant.Thus

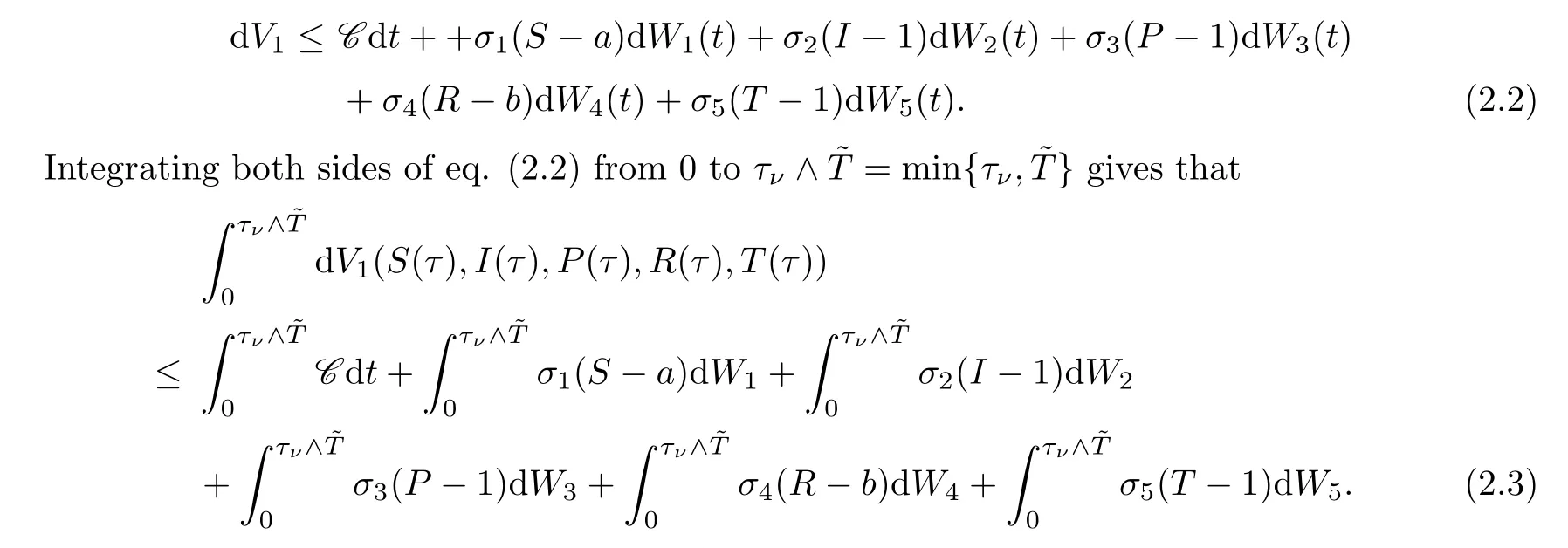
Taking expectations on both sides of (2.3) yields

Let Ων=｛τν≤｝for allν≥ν1.Then,as stated by (2.1),P(Ων) ≥ε.Observe that for everyω∈Ωνthere exist at leastS(τν,ω) orI(τν,ω) orP(τν,ω) orR(τν,ω) orT(τν,ω) that equals eitherνor,since

Hence,we have that

It follows from (2.4) that

where1Ωνis the indicator function of Ων(ω).Lettingν→∞leads to the contradiction that

and hence we obtain thatτ∞=∞a.s.,which completes the proof of Theorem 2.1. □

Remark 2.2In May 2016,the WHO unveiled the ‘Global Health Sector Strategy on Viral Hepatitis,2016-2021’.The strategy laid out a vision of eradicating viral hepatitis as a public health problem,and the global targets being to reduce new viral hepatitis infections by 90% and reduce deaths due to viral hepatitis by 65% by 2030 [20].Hence,it is essential to study the eradication of the hepatotropic RNA virus among chronic infected HCV individuals.This is the subject of the next section.

3 Extinction of the HCV

The spread of the disease and the natural mortality rate of the population,and also the intensities of the white noise in the stochastic system (1.2),are the factors that need to be considered to wipe out HCV.First,we shall present a lemma which will be used in our analysis.

Lemma 3.1Let (S(t),I(t),P(t),R(t),T(t)) be the solution to stochastic HCV system(1.2) with any positive initial values (S(0),I(0),P(0),R(0),T(0)) ∈Then

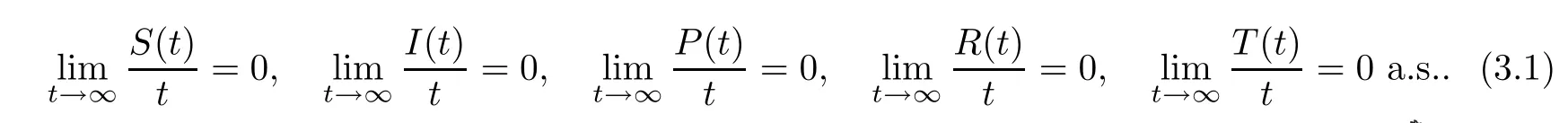
The proof of the Lemma 3.1 is similar to that of Lemma 2.1 and Lemma 2.2 in [37],so we omit it.

Theorem 3.2Let (S(t),I(t),P(t),R(t),T(t)) be the solution of stochastic HCV system(1.2) with any positive initial values (S(0),I(0),P(0),R(0),T(0)) ∈.If

then the HCV in stochastic system (1.2) is eradicated exponentially with probability one;i.e.,

By stochastic system (1.2),we have that

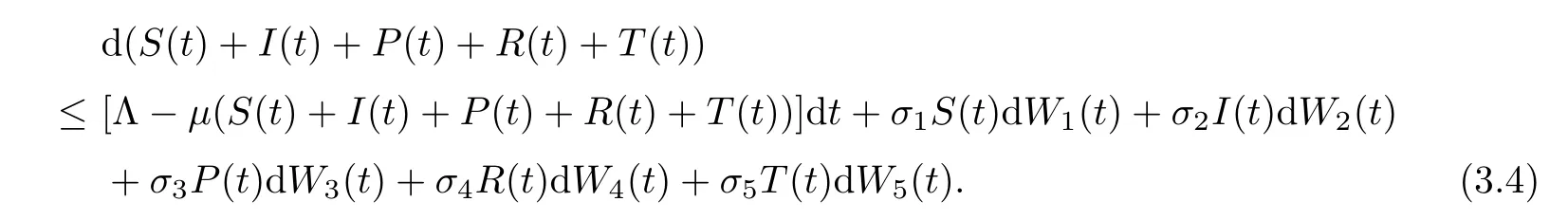
Integrating both sides of (3.4) from 0 tot,with (3.1) and (3.2),we get that

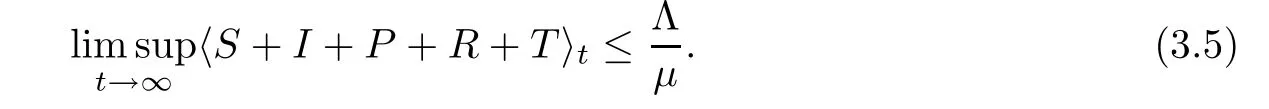
Integrating both sides of (3.3) from 0 tot,and combining with (3.5) andwe attain that

which confirms that

Otherwise,according to (3.4),we have that

which,together with (3.1),(3.2) and (3.7),yields that

Remark 3.3Theorem 3.2 shows the eradication of the hepatotropic RNA virus in stochastic HCV system (1.2) when.For instance,we opt for the environmental white noisesσ1=0.1,σ2=0.4,σ3=0.3,σ4=0.3,σ5=0.3 and other parameters as follows:

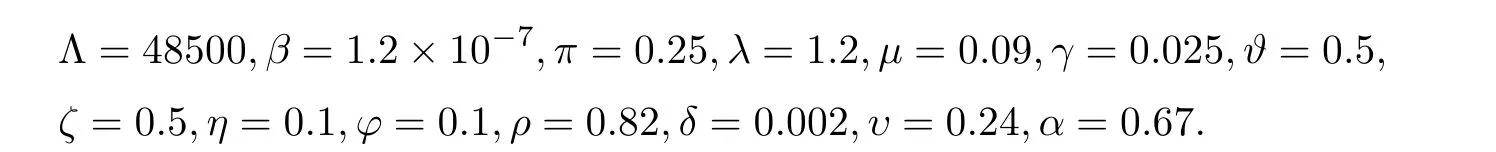
Figure 1 Simulations of stochastic HCV model (1.2) with initial conditions (S(0),I(0),P(0),R(0),T(0))=(0.8,0.18,0.12,0.1,0.1).The parameter values used are as given in Remark 3.4,with σ1=0.1,σ2=0.4,σ3=0.3,σ4=0.3 and σ5=0.3.

Remark 3.4After six months of persistence of hepatitis C RNA virus within the blood,acute HCV individuals will progress to chronic HCV infection.At this stage,they have low levels of immunity.These are the factors regarding the persistence of HCV amongst the population.HCV persistence is addressed in the next section.

4 Ergodic Stationary Distribution

When considering epidemiological dynamical systems,we are interested in when the disease will persist and prevail in a population.In this section,we present some theories about stationary distribution (see Has’minskii [19]),and we show that there exists an ergodic stationary distribution which reveals when a disease will persist.LetX(t) be a homogeneous Markov process in Rd,described by the following stochastic differential equation:

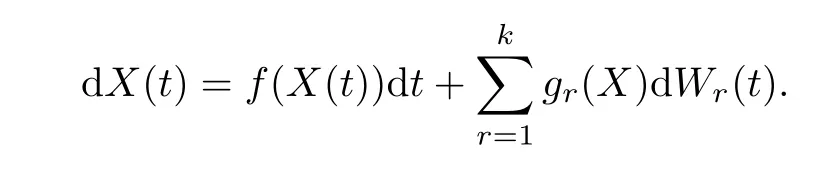
The diffusion matrix is defined as

Lemma 4.1(see [19]) The Markov processX(t) has a unique ergodic stationary distributionπ(.) if there exists a bounded domainD⊂Rdwith a regular boundary Γ having the following properties:

A1: there is a positive numberMsuch that,forx∈D,ξ∈Rd;

A2: there exists a non-negative C2-functionV(x) such that LVis negative for anyx∈RdD.Then

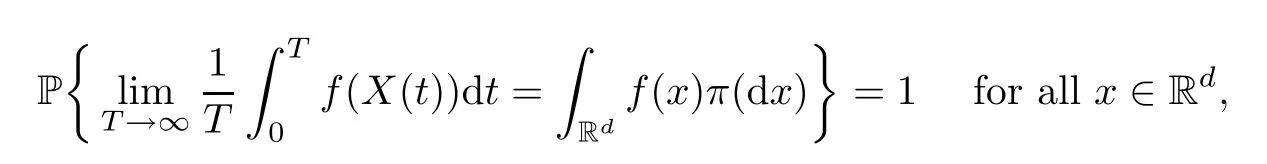
wheref(.) is a function integrable with respect to the measureπ.

Define a parameter

Theorem 4.2Assuming that,for any initial values (S(0),I(0),P(0),R(0),T(0))∈,stochastic HCV system (1.2) admits a unique stationary distributionπ(.),and it has the ergodic property.

ProofTo prove Theorem 4.2,it suffices to validate conditions A1and A2of Lemma 4.1.The diffusion matrix of stochastic HCV system (1.2) is given by

Next,we focus to proving condition A2.Define

whereci(i=1,2,···,9) are positive constants to be resolved later.By virtue of It’s formula onU1,we get that

wherec10,c11,c12andc13are positive constants to be determined later.

From (4.1),we have that

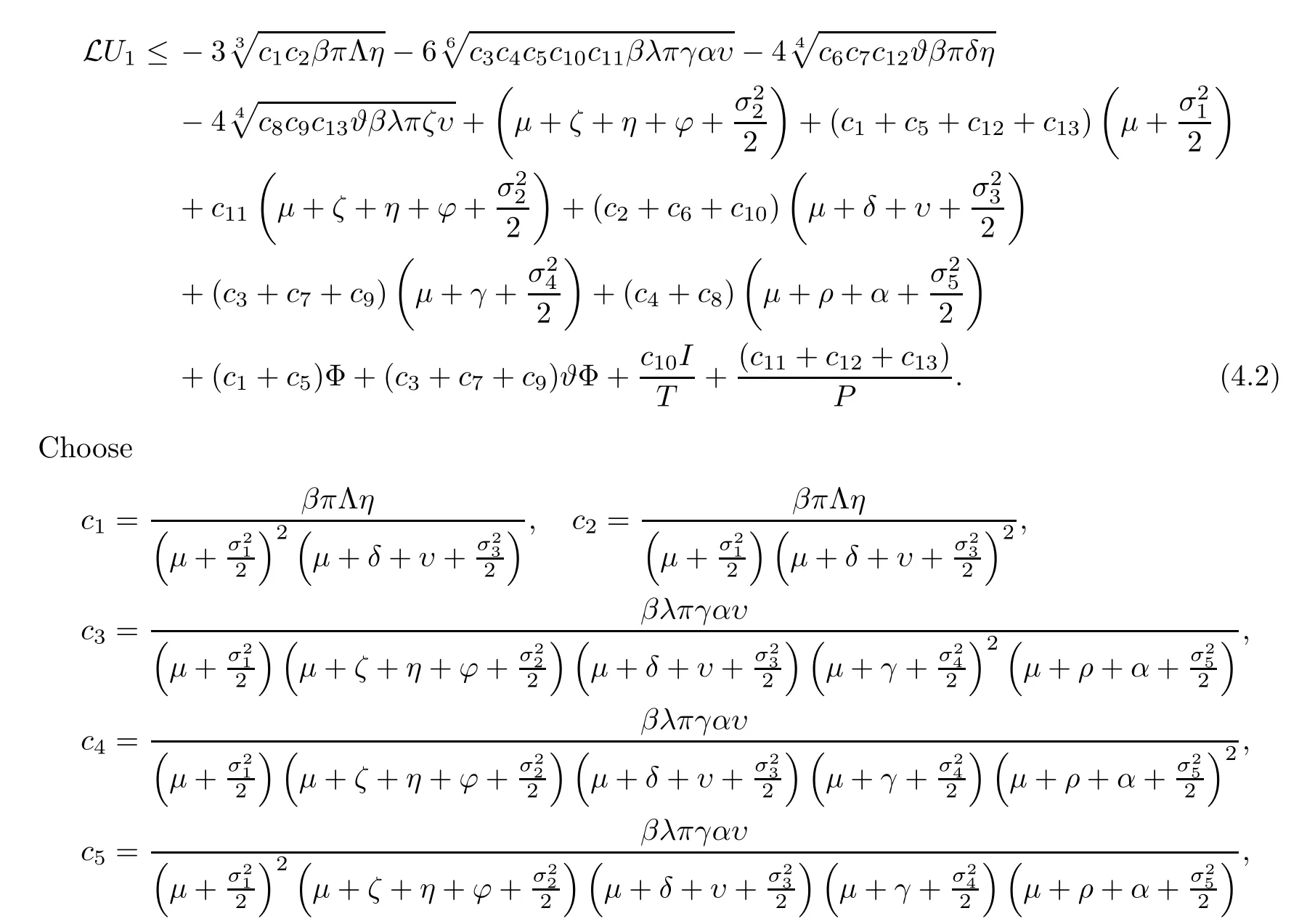
Consider,k1=c1+c5,k2=c3+c7+c9,k3=c10andk4=c11+c12+c13.It follows that

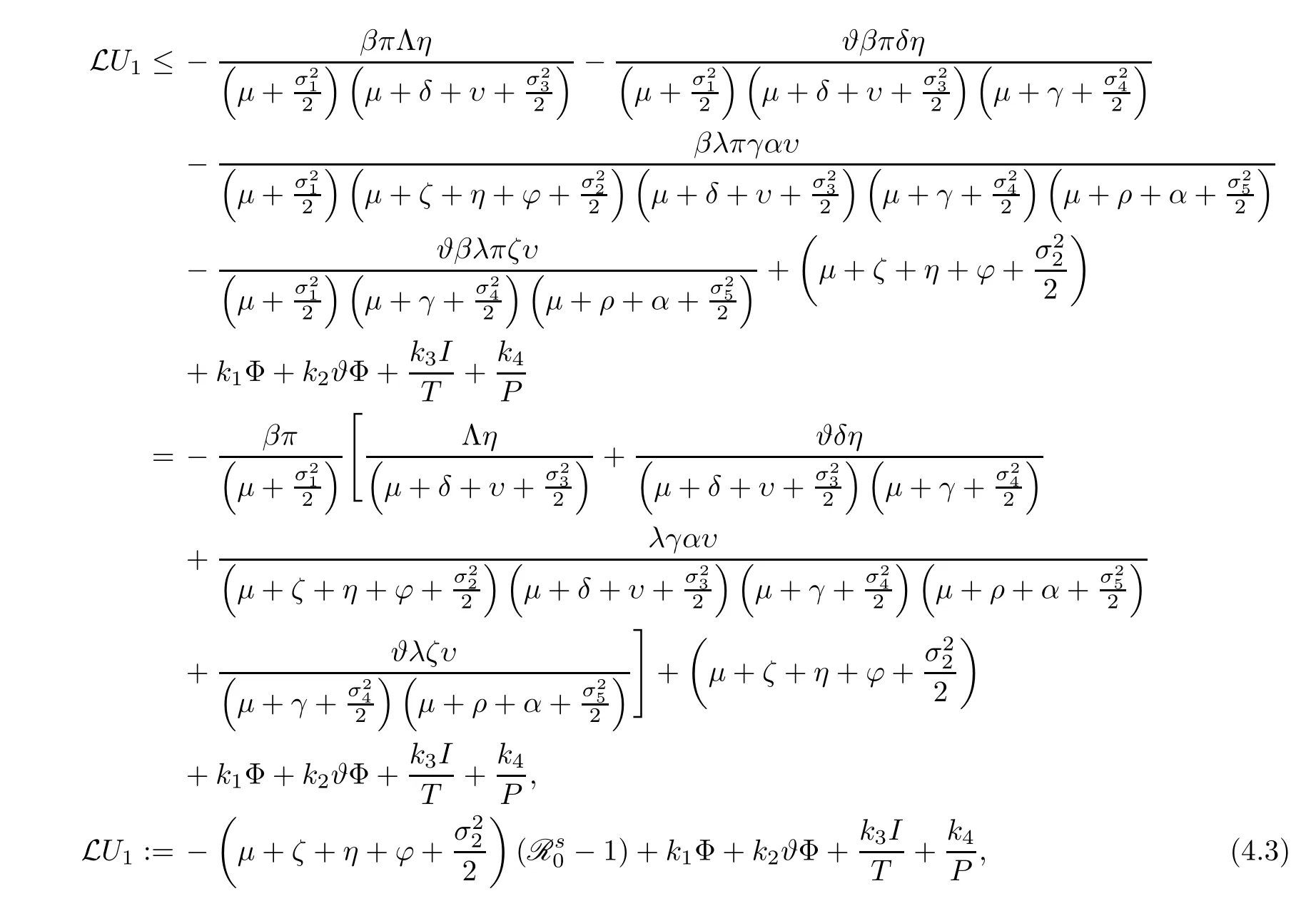
Define a C2-functionQ(S,I,P,R,T):→R as

Moreover,Q(S,I,P,R,T) is not only continuous,but also tends to ∞as (S,I,P,R,T) approaches the boundary ofand as ||(S,I,P,R,T)|| →∞,where ||.|| denotes the Euclidean norm of a point in;consequently,it must be lower bounded and attain this lower bound at a pointin the interior of.Then we can define a non-negative C2-functionas follows:

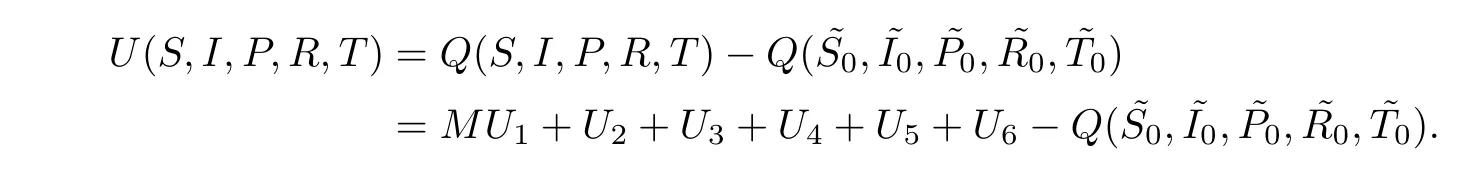
Applying Itˆo’s formula,we have that

Similarly,we have that

In view of (4.3),(4.5),(4.6),(4.7),(4.8) and (4.9),we obtain that

Now we are in position to construct a compact subset D∈such that the condition A2in Lemma 4.1 holds.Define the bounded closed set

where 0＜∈＜1 is a sufficiently small constant.In the set D∈,we can choose∈sufficiently small such that the following conditions hold:

HereFis a positive constant which will be given explicitly in expression (4.19).Conveniently,we can divide D∈into the following ten domains:

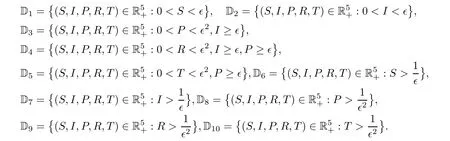
Case 1If (S,I,P,R,T) ∈D1,in view of (4.10),one can see that

This follows from (4.11).

Case 2If (S,I,P,R,T) ∈D2,we obtain that

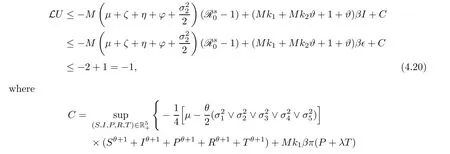
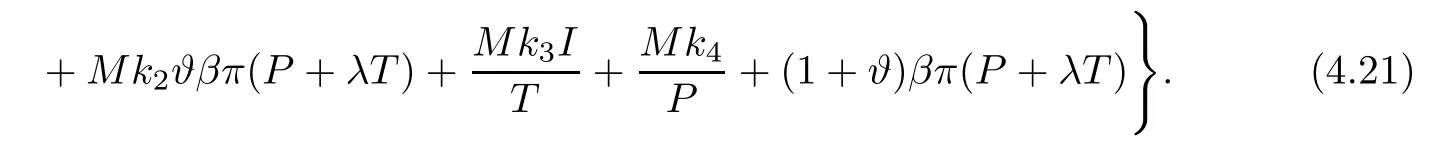
This follows from (4.4) and (4.12).

Case 3If (S,I,P,R,T) ∈D3,as a consequence of (4.10),we get that

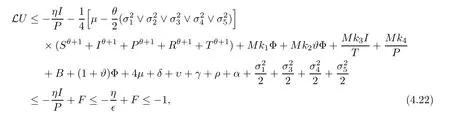
which follows from (4.13).

Case 4If (S,I,P,R,T) ∈D4,from (4.10),we can attain that

which follows from (4.14).

Case 5If (S,I,P,R,T) ∈D5,in connection with (4.10),we derive that

which follows from (4.15).

Case 6If (S,I,P,R,T) ∈D6,owing to (4.10),we have that

which follows from (4.16).

Case 7If (S,I,P,R,T) ∈D7,on account of (4.10),we attain that

which follows from (4.16).

Case 8(S,I,P,R,T) ∈D8coupled with (4.10) yields that

which follows from (4.17).

Case 9If (S,I,P,R,T) ∈D9,by (4.10),one can obtain that

which follows from (4.17).

Case 10If (S,I,P,R,T) ∈D10,by (4.10),one can obtain that

which follows from (4.17).

Obviously,from (4.18),(4.20),(4.22),(4.23),(4.24),(4.25),(4.26),(4.27),(4.28) and (4.29),we attain that for a sufficiently small∈,LU(S,I,P,R,T) ≤-1,∀(S,I,P,R,T) ∈ D∈.Hence the condition A2of Lemma 4.1 holds.It follows from Lemma 4.1 that stochastic system(1.2) is ergodic and has a unique stationary distributionπ(.).This completes the proof. □

Remark 4.3Theorem 4.2 affirms that stochastic HCV system (1.2) has a unique ergodic stationary distributionπ(.) if

Notice that the expression ofconverges with the basic reproduction number R0for the deterministic model (1.1) if the environmental white noise is not taken into account.For example,we fix the parameters as follows: Λ=48500,β=0.025,π=8.47 × 10-5,λ=0.5,μ=0.005,γ=0.5,ϑ=0.4,ζ=0.005,η=0.0007,φ=0.008,ρ=0.5,δ=0.0001,υ=0.8,α=0.9 withσ1=0=σ2=σ3=σ4=σ5.We do this by calculating=1.3366 and R0=1.3369.Otherwise,we choose the above parameters exceptβ=5 × 10-7,π=0.8,μ=0.001,η=0.07 and the environmental white noisesσ1=0.15,σ2=0.14,σ3=0.2,σ4=0.1,σ5=0.2.We have that=1.4405.Figure 2 reflects the first and second segments of the figures,which confirms the existence of the unique stationary distribution of stochastic HCV model (1.2) and the probability distribution of the stationary distribution,respectively.

Figure 2 The first and second segments of the figures show the existence of the unique stationary distribution of stochastic HCV model (1.2) with initial conditions (S(0),I(0),P(0),R(0),T(0))=(0.8,0.18,0.12,0.1,0.1),and the probability distribution of the stationary distribution,respectively.

5 Numerical Simulations and Discussions

In this article,we have explored a stochastic epidemic hepatitis C virus model with a chronically infected treated population.We showed that the stochastic HCV system (1.2) has a unique global positive solution.We attained sufficient conditions for the extinction of the hepatotropic RNA virus.Furthermore,we accomplished sufficient conditions for the existence of a unique ergodic stationary distribution of the positive solutions to the stochastic HCV model(1.2) by obtaining a suitable Lyapunov function.

For better understanding,the effect of varied environmental noise on the model’s dynamic behavior based on real-life parameters is examined through numerical simulations.We apply Milstein’s Higher order method [45] to find the solution (1.2) with initialS(0)=0.8,I(0)=0.18,P(0)=0.12,R(0)=0.1,T(0)=0.1,and suppose that the unit of time is one day.The stochastic HCV model can be written in terms of the subsequent discretization equations:

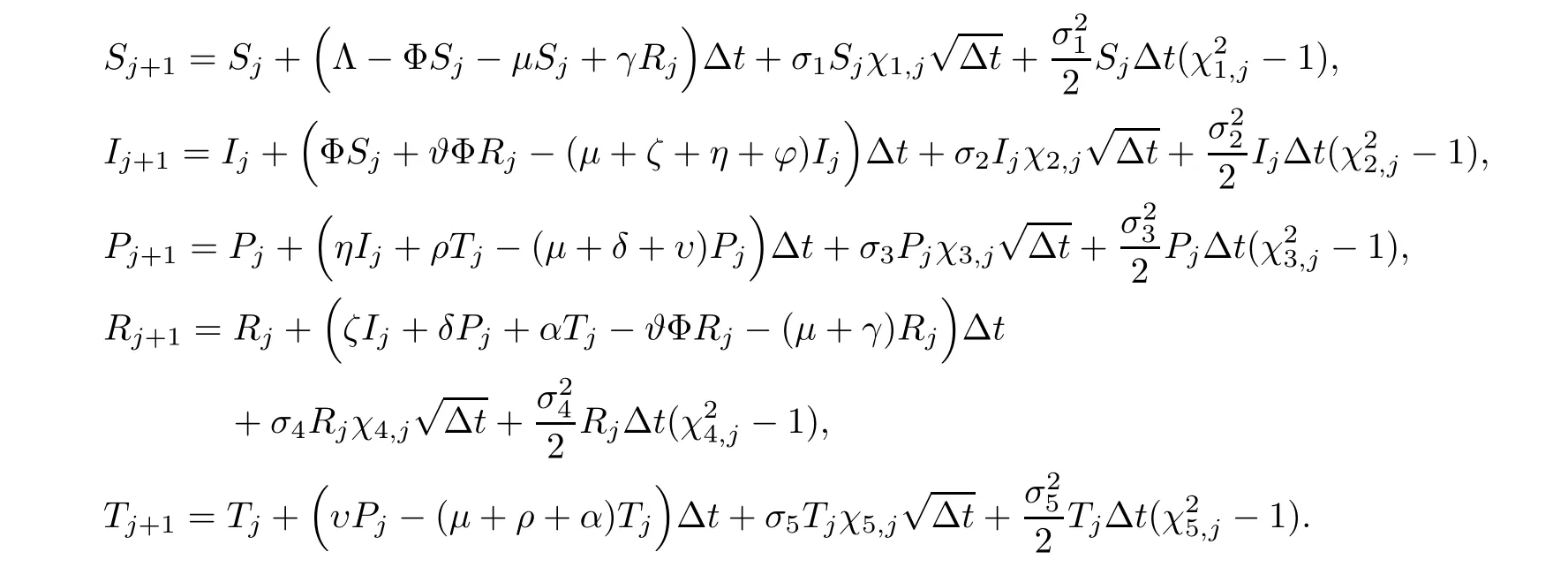
Hereχi,j(i=1,···,5),j=1,2,···,nare the independent Gaussian random variables which follow the distributionN(0,1),and0 reflects the intensities of white noise.Consider the time step Δt=0.02.

We choose the parameter values of stochastic HCV system (1.2) as given in Table 2 and the intensities of environmental noiseσ1=0.2,σ2=0.2,σ3=0.3,σ4=0.2,σ5=0.3.

Noting that

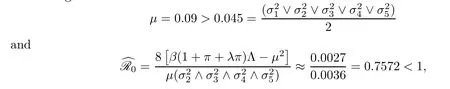
the conditions of Theorem 3.2 are verified (see Figure 3).On the other hand,Theorem 3.2 shows that the HCV in stochastic system (1.2) is eradicated exponentially with probability one.Furthermore,increasing the disease transmission rate from 2.1×10-7to 4×10-4,decreasing the rate of progression to chronic infection,decreasing the treatment failure rate of the chronically infected population etc.,are all factors that can affect the chances of HCV growing from acute infection to chronic infection.Keeping all the parameter values the same as in Table 2,we can expectβ=4 × 10-4,π=0.008,η=0.7,ρ=0.5,δ=0.012,υ=0.34 with the intensities of environmental white noise as follows:

Figure 3 Simulations of stochastic HCV model (1.2) with initial conditions (S(0),I(0),P(0),R(0),T(0))=(0.8,0.18,0.12,0.1,0.1).The parameter values used are as given in Table 2,with σ1=0.2,σ2=0.2,σ3=0.3,σ4=0.2 and σ5=0.3

By computation,

and the conditions of Theorem 4.2 are fulfilled (see Figure 4).Take another set of parameter values the same as in Table 2,exceptβ=0.005,π=6 × 10-4,η=0.7,ρ=0.5,δ=0.012,υ=0.34 withσ1=0.2,σ2=0.1,σ3=0.2,σ4=0.1,σ5=0.2,by determining that=1.2304＞1.Note that the small intensities of environmental white noise lead to disease persistence,while large intensities of environmental white noise may be helpful for suppressing disease outbreak and eradicating the hepatotropic RNA virus.

Table 2 List of parameters

Figure 4 The existence of the unique stationary distribution of stochastic HCV model (1.2)

In future work,we will concentrate on some more realistic but complex models,such as considering the effects of impulsive perturbations on system (1.2).Theorem 3.2 shows that the disease in eradicates in acute and chronically infected populations if we have the condition.What is the behavior of stochastic HCV system (1.2) in the case wherein Theorem 3.2? On the other hand,we could put some other environmental noises,like Poisson noise,Lévy noise and so on,into system (1.2),and examine the dynamical performance of the system.

In any case,mathematical models pertaining to pathology and epidemiology must always keep environmental noise in mind.