EXISTENCE RESULTS FOR THE KIRCHHOFF TYPE EQUATION WITH A GENERAL NONLINEAR TERM*

School of Mathematics and Information,Guangxi University,Nanning 530004,China

E-mail: huirongpi2001@163.com;274152148@qq.com

Abstract This paper is mainly concerned with existence and nonexistence results for solutions to the Kirchhofftype equationin R3,with the general hypotheses on the nonlinearity f being as introduced by Berestycki and Lions.Our analysis introduces variational techniques to the analysis of the effect of the nonlinearity,especially for those cases when the concentration-compactness principle cannot be applied in terms of obtaining the compactness of the bounded Palais-Smale sequences and a minimizing problem related to the existence of a ground state on the Pohozaev manifold rather than the Nehari manifold associated with the equation.

Key words Kirchhofftype equation;general nonlinearity;variational methods;Pohozaev identity

1 Introduction

We are concerned with the nonlinear Kirchhofftype problem

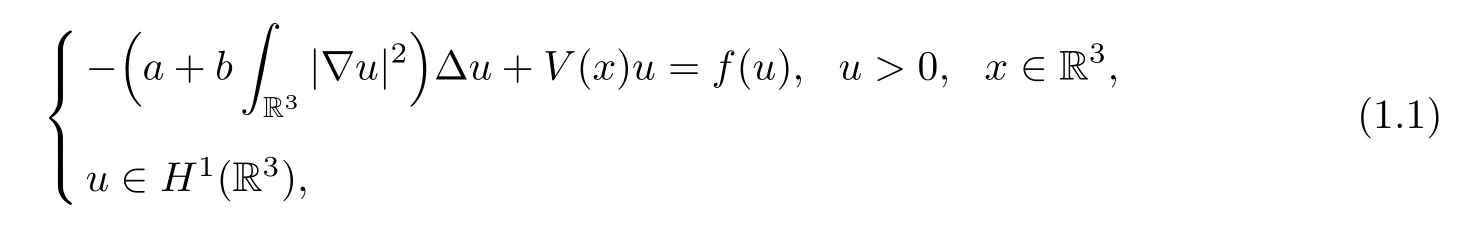
wherea ＞0,b≥0 are two constants andV: R3→R is a potential function satisfying that

(V1)V(x) ∈C1(R3,R) is a nonnegative function with

(V2) there exists a constantα∈(0,a) such thatfor allx∈R3{0};

(V3)Vis radially symmetric;

(V4) ∇V(x) ·x≤0,for allx∈R3;

(V5) 3V(x)+∇V(x) ·x≥0 for allx∈R3,and the strict inequlity holds for some subset of R3with a positive Lebesgue measure.

Moreover,we assume that the functionfsatisfies the following hypotheses:

(f1)f∈C(R,R) is an odd function;

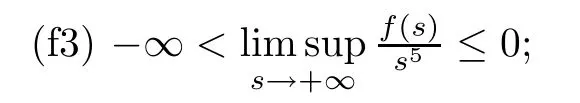
(f4) there existsζ ＞0 such thatf(s)ds ＞0.

The above general hypotheses on the nonlinearityfintroduced by Berestycki and Lions [3] do not require superlinear growth at infinity.

Problem (1.1) arises in an interesting physical context.Indeed,if we establish thatV(x)=0 and replace R3by a bounded domain Ω ⊂R3in (1.1),then we have the following KirchhoffDirichlet problem:

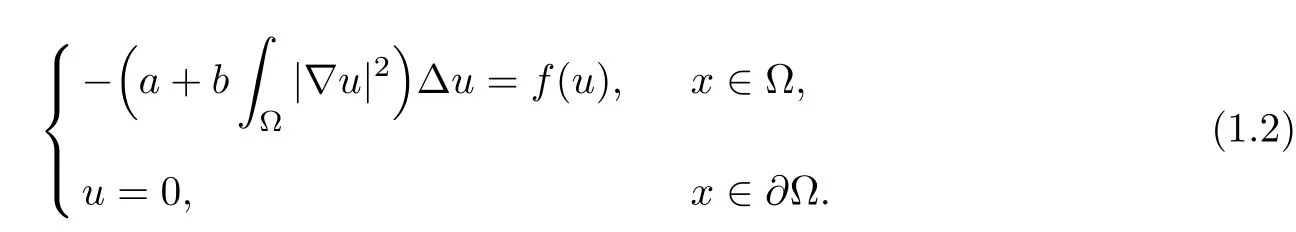
This is related to the stationary analogue of the equation

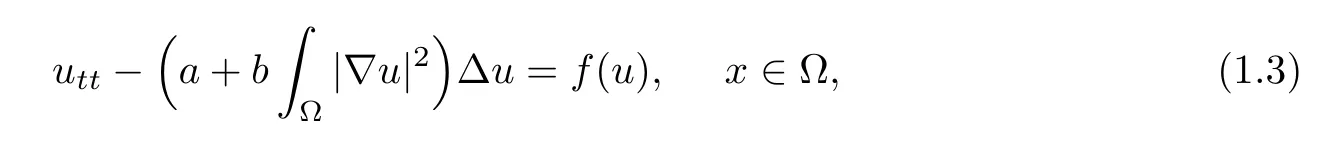
which was first proposed by Kirchhoff[12] as an extension of the classical d’Alembert wave equation for describing the transverse oscillations of a stretched string.It is pointed out that problem (1.3) also appears in fields such as biological systems,whereudescribes a process which depends on the average of itself (for example,population density;see [5]).Mathematically,problem (1.1) is a nonlocal problem as the appearance of the termimplies that (1.1)is not a pointwise identity.This causes some mathematical difficulties,but also makes the study of such a problem particularly interesting.For more mathematical and physical background regarding problem (1.1),we refer readers to the papers [1,4,6,9,12,13,20] and the references therein.After the pioneering work by J.-L.Lions [14],where an abstract functional analysis approach was introduced to the equation (1.3),the Kirchhofftype equation has received much more attention.

Recently,the Kirchhofftype equation

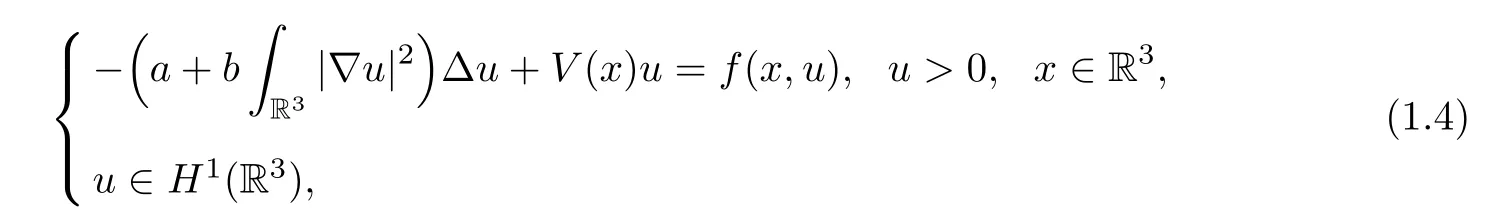
wherea ＞0,b ＞0 are constants andV: R3→R,f∈C(R3× R,R),has been studied extensively by many researchers.Let us briefly comment on some of those that are related to our work.Wu [21] obtained the existence of nontrivial solutions to (1.4) by proving that the Palais-Smale condition holds whenf(x,u) satisfies the Ambrosetti-Rabinowitz type condition

(ART) there existsμ ＞4 such that 0＜μF(x,s) ≤sf(x,s),∀s ＞0,where

Vsatisfies

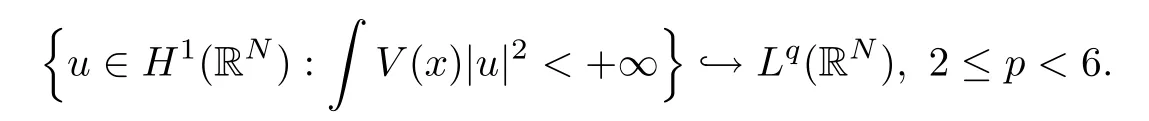
He and Zou [9] considered the problem (1.1) withf(u)=|u|p-2u,4＜p ＜6 satisfying (ART),and they proved the existence of a ground state solution by using the Nehari manifold under the assumption that

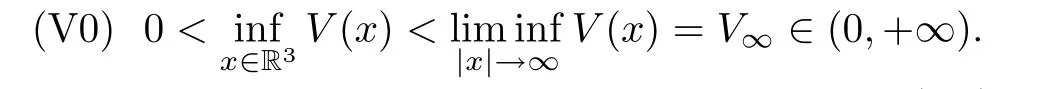
Later on,some researchers considered the problem (1.1) withf(u)=|u|p-2u,2＜p≤4.In this case,it is difficult to get a bounded Palais-Smale sequence,hence arguments used above do not work any more.Li and Ye [13] studied thatf(u)=|u|p-2u,3＜p≤4,using a monotonicity trick,and with a new version of a global compactness lemma,they proved that(1.1) has a ground state solution.Then Guo [8] defined a new Nehari-Pohozaev manifold,different from that in [13],and generalized the result in [13] to the general nonlinearityf(u)andf∈C1(R3,R),including the casef(x,u)=|u|p-2u,2＜p≤4.The result of [8] was later extended by Tang and Chen in [20].They presented some new arguments for substituting the assumptionf∈C(R3,R) and the weak version monotonicity assumption onf.

Whenb=0,equation (1.1) does not depend on the nonlocal term anymore,it becomes the steady state of the nonlinear Schrdinger equation,which has been extensively studied in the last three decades,especially regarding the existence of positive solutions,multiple solutions,ground states and semiclassical states.Most of those results rely on the assumptions (V0) and the classical Ambrosetti-Rabinowitz condition onf,namely,

(CAR) there existsμ ＞2 such that 0＜μF(s) ≤sf(s),∀s ＞0,whereIt is well known that whenfsatisfies the classical Ambrosetti-Rabinowitz condition (CAR)andVsatisfies (V0),a standard method [7,15] to look for the ground state solution for (1.1)withb=0 is to study the minimizing problem on the Nehari manifold.On the other hand,if,∀x∈R3,the concentration-compactness principle cannot be applied for obtaining the compactness of the bounded Palais-Smale sequences,and the minimizing problem on the Nehari manifold cannot be solved.However,if the nonlinear term satisfies (f1)–(f4),a similar study can be done by replacing the Nehari manifold with the Pohozaev manifold;see also [2,11,16].

Inspired by the above,especially by the works [2,8,20],in the present paper,we consider the Kirchhofftype equation with the nonlinear termfsatisfying (f1)–(f4),which partially improves the result of Guo [8],and establishes the existence of positive solutions and the nonexistence of ground state solutions.To our knowledge,this case seems to have been considered by few authors,so the results in this paper are new.The hypotheses (f1)–(f4) onfdo not require the superlinear growth at infinity,but bring some difficulties for dealing with the boundedness of the Palais-Smale sequences.The assumptions (V1)–(V3) onVmean that the new Nehari-Pohozaev manifold introduced in [8,13,20] and the concentration-compactness principle cannot be used.The nonlocal term gives us a big challenge and the existence result to (1.1),which can also be viewed as an extension of the result of Azzollini and Pomponio [2] concerning (1.1) with the caseb=0.We remark that we do not assume either,which is needed in[8,20],or the (CAR) condition on the nonlinearity.

To give the results of this paper,we will use the following notations:

·H1(R3) is the usual Sobolev space endowed with the norm

·Hr1(R3) :={u∈H1(R3) :u(x)=u(|x|)};

· the functionalI(u) is associated to the equation (1.1);

· P is the Pohozaev manifold related to equation (1.1).

The first main result can be stated as follows:

Theorem 1.1Assume that (V1)–(V3) and (f1)–(f4) hold.Then the problem (1.1) has a radially symmetric solutionu∈Hr1(R3).

As a consequence of Theorem 1.1,we can prove

Theorem 1.2Assume that (V1)–(V3) and (f1)–(f4) hold.Then the problem (1.1) possesses a radial ground state solution,namely a solution minimizing the action among all of the nontrivial radial solutions inHr1(R3).

In the third part of the paper,we are interested in solving a minimization problem strictly related to the existence of a ground state for (1.1).We get the following result

Theorem 1.3Assume that (V1)(V2)(V4)(V5) and (f1)–(f4) hold.Thenis not a critical level forI.In particular,the infimumpis not achieved.

Remark 1.4An example ofVsatisfying (V1)(V2)(V4)(V5) is,with a constantk ＞0.From (V2),we know that

This paper is organized as follows: in Section 2,we give some preliminary results and existence theorems.Then in Section 3,we obtain the nonexistence result.

2 Some Preliminary Results and Existence Results

We do some modifications onf.Following [3],defines0=min{s∈[ζ,+∞)|f(s)=0}.Iff(s)0 for anys≥ζ,we denotes0=+∞,and assume that the function: R →R satisfies

Note that,by the maximum principle,a solution of problem (1.1) within place offis a solution of (1.1) for the original functionf.Hereafter we shall consider thatfis defined as in(2.1) that (f1),(f2),(f4) andhold.Furthermore,we set,for anys≥0,

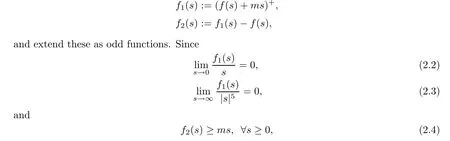
we have that,for anyε ＞0,there existsCε＞0 such that

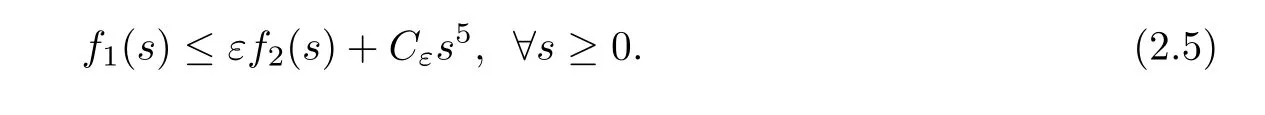
Under the conditions (V1)–(V3) and (f1)–(f4),and according to the critical point theorem,solutions of (1.1) are the critical points of the functionalI:H1(R3) →R given by

Using an indirect approach from [10],we first look for the bounded Palais-Smale sequences of the perturbed functionals

for almost allλnear 1.Then we will deduce the existence of a nontrivial critical pointuλof the functionalIλat the mountain pass levelCλ,defined below.Next,by the assumptions on V,we prove the boundedness ofuλn,which is a bounded Palais-Smale sequence forI:=I1obtained by an approximation procedure,and the convergence of the sequence {uλn},asλn→1,to get the solution of (1.1).

We will apply the following slightly modified version of [10,Theorem 1.1] (see [2,Theorem 3.1]):

Theorem 2.1Let (X,‖·‖) be a Banach space and letJ⊂R+be an interval.We consider a family ofC1functionals onXof the form

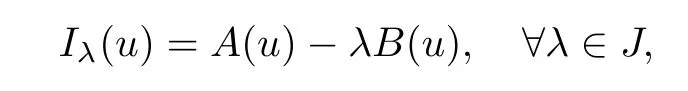
withB(u) ≥0,∀u∈X,and eitherA(u) →+∞orB(u) →+∞as ‖u‖ →+∞,and such thatIλ(0)=0.We define,for anyλ∈J,

If,for everyλ∈J,the set ΓλØ and

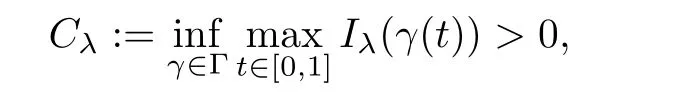
then,for almost everyλ∈J,there is a bounded (PS)Cλsequence inX.

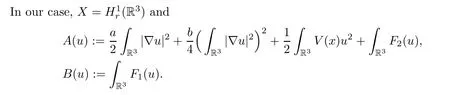
In order to apply Theorem 2.1,we need to choose a suitable intervalJsuch that ΓλØ for anyλ∈J,andCλ＞0.

According to [3],we get that there exists a functionz∈H1r(R3) such that

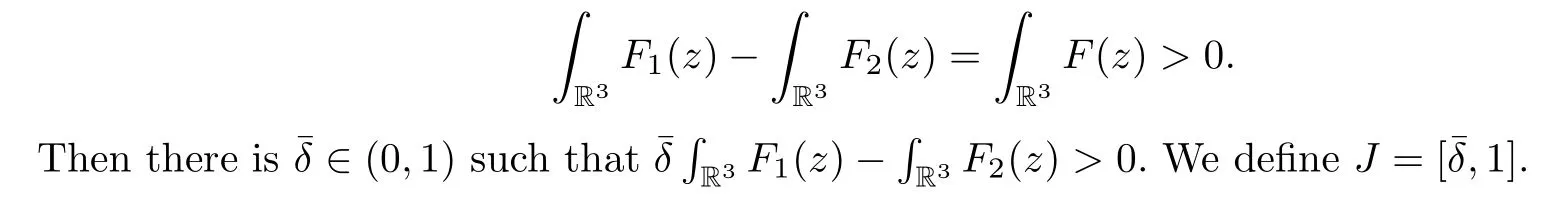
Lemma 2.2For everyλ∈J,we have the set Γλ≠Ø.

ProofLetλ∈J.Set＞0 sufficiently large.Definein the following way:

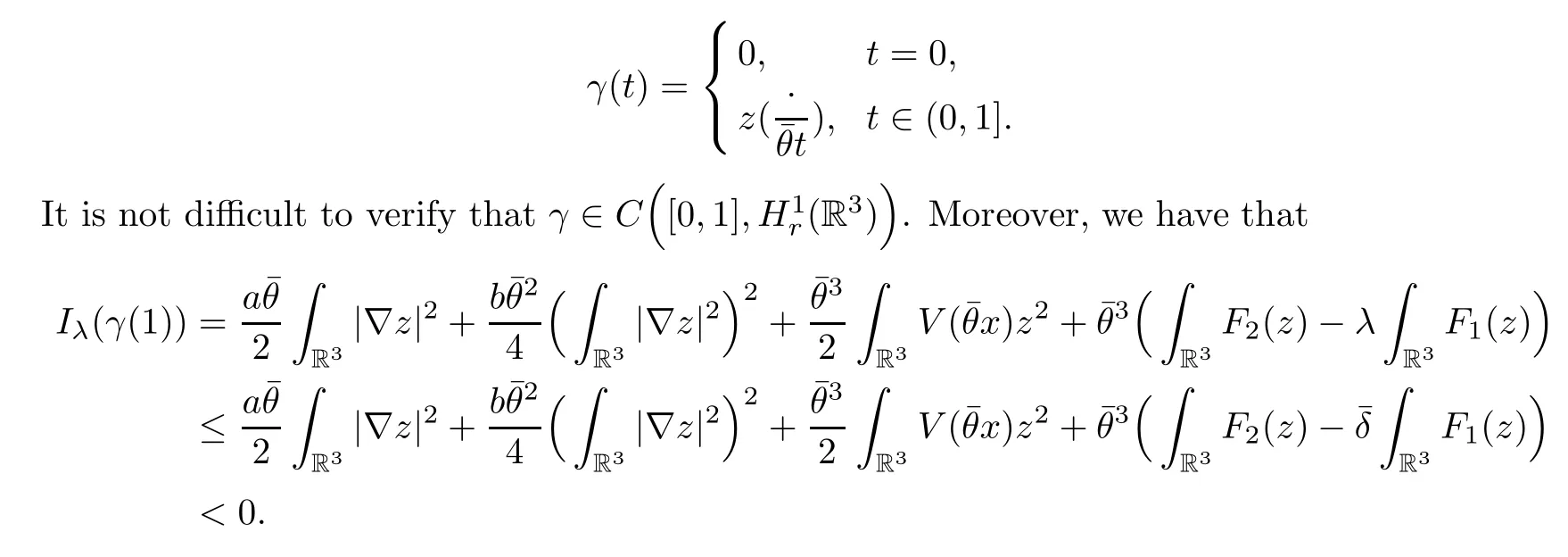
The last inequality holds for (V1) and＞0 sufficiently large.This implies thatγ(t) ∈Γλ,for allλ∈J. □

Lemma 2.3There exists a constantσ ＞0 which is independent ofλsuch thatCλ≥σ ＞0 for anyλ∈J.

ProofFor anyu∈andλ∈J,according to (V1),(2.6) and (2.7),we get that

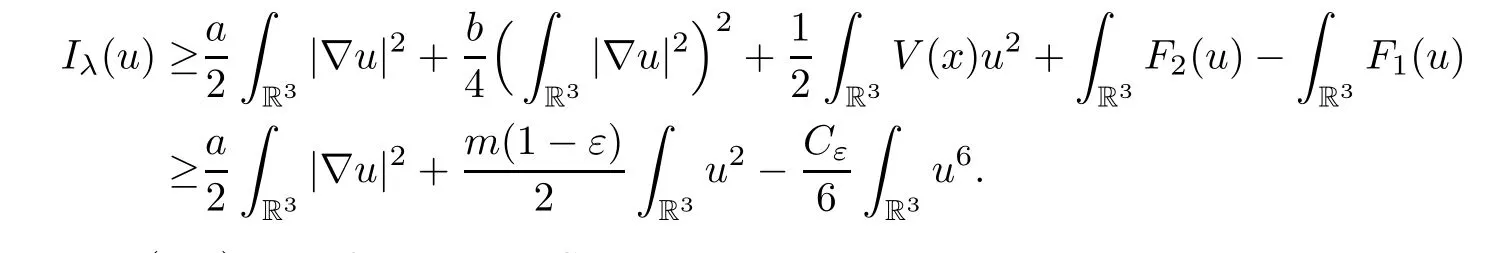
Chooseε∈(0,1) and fix,by the Sobolev embedding theorem,that there existρ ＞0 andσ ＞0 such thatIλ(u) ≥σ ＞0 for ‖u‖=ρandIλ(u)＞0,if 0＜‖u‖＜ρ.Note that,for anyλ∈J,γ∈Γλ,γ(0)=0 andIλ(γ(1))＜0,one has that ‖γ(1)‖＞ρ.By the continuity ofγ,we deduce that there existstγ∈(0,1) such that ‖γ(tγ)‖=ρ.Therefore,∀λ∈J. □

We present a variant of the Strauss Compactness Lemma,which plays an important role in the existence of solutions.

Lemma 2.4Assume thatP(x),Q(x) ∈C(R,R) satisfies,and assume thatvn,vandzare measurable functions from R3to R,withzbounded,such that

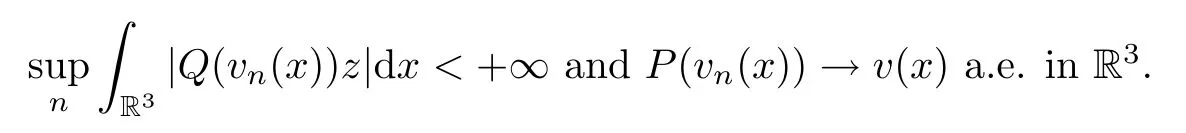
Then ‖(P(vn)-vz‖L1(B)→0 for any bounded Borel setB.Furthermore,if we also have that,then ‖(P(vn) -v)z‖L1(R3)→0.

The proof of Lemma 2.4 is similar to that of Theorem A.I in [3],so it is omitted here.

Lemma 2.5For anyλ∈J,any bounded Palais-Smale sequence for the functionalIλcontains a convergent subsequence.

ProofLetλ∈Jand {un} be a bounded Palais-Smale sequence forIλ.Up to a subsequence,we can assume that there existsu∈such that

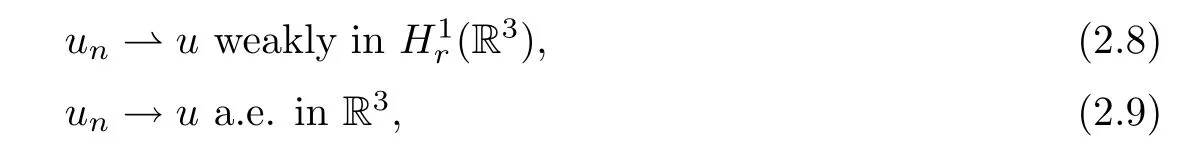
by using the fact thatis compactly embedded intoLq(R3) for 2 ≤q ＜6.

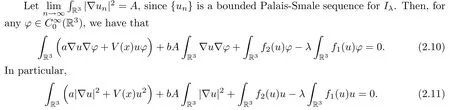
By (2.2),(2.3),the well-known Strauss Radial Lemma (see [17]) and by applying Lemma 2.4 forvn=un,v(x)=f1(u)u,P(s)=f1(s)s,Q(s)=s2+s6andz=1,we have that

From (2.11),we deduce that

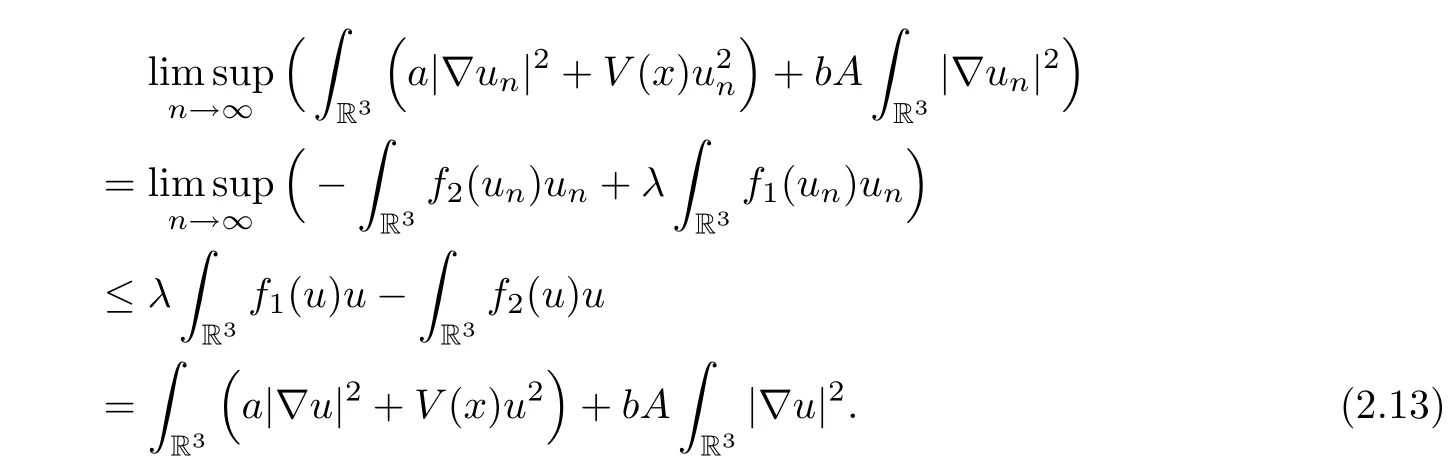
On the other hand,by weak lower semicontinuity,we have that

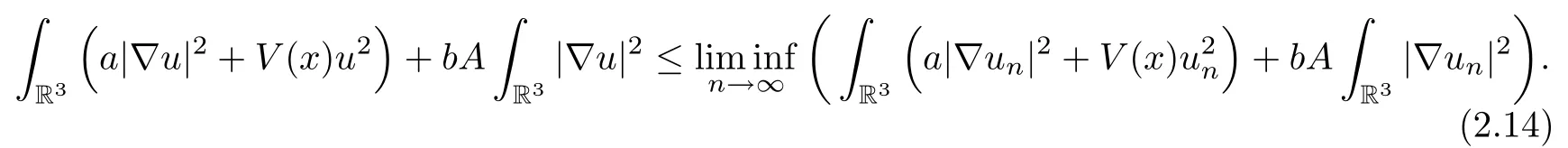
By (2.12),(2.13) and (2.14),since

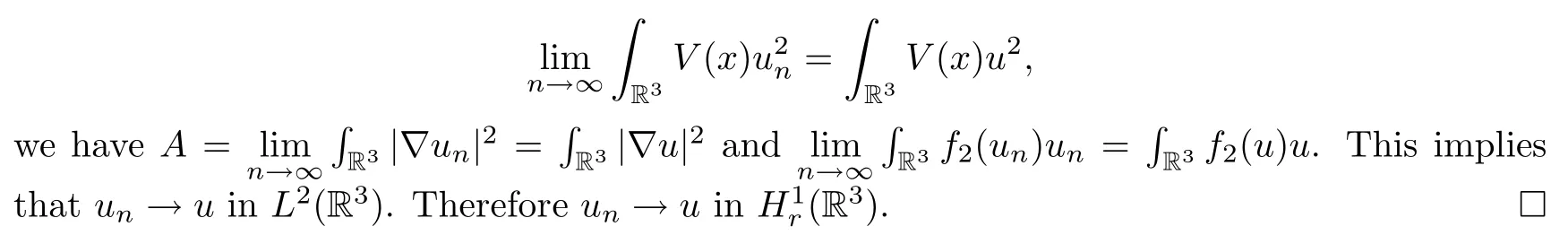
Using Theorem 2.1 and Lemma 2.5,we obtain the following desired result:

Lemma 2.6For almost everyλ∈J,there existsuλ∈Hr1(R3){0} such thatIλ(uλ)=Cλand (Iλ)′(uλ)=0.

From (2.15),(V2) and the fact thatIλn(un)=Cλn,we have that

Noting thatCλ≤C¯δfor anyλ∈J,we get that {|∇un|} is bounded inL2(R3).On the other hand,by (2.5) and the fact that,for anyε∈(0,1),there existsCε＞0 such that

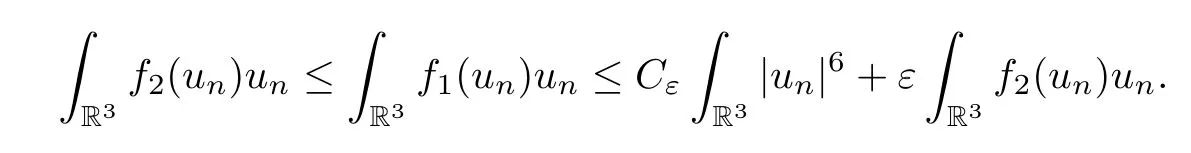
Therefore,by (2.4) and the Sobolev embedding,we get that

Moreover,from Lemma 2.3,Iλn(un)=Cλnand the boundedness of {un},we deduce that

Therefore,{un} is a Palais-Smale sequence for the functionalI,and by Lemma 2.5,uis a nontrivial solution for (1.1).Furthermore,by standard arguments [18,19],we can use the strong maximum principle to get thatu ＞0. □

In order to prove Theorem 1.2,we set

Lemma 2.7sr＞0.

ProofIffsatisfies (f1)–(f4),according to (2.5),we have,for anyu∈Sr,ε∈(0,1) fixed,that

whereCε,C ＞0.Therefore,we deduce that.Note that,for anyu∈Sr,by(V2) and

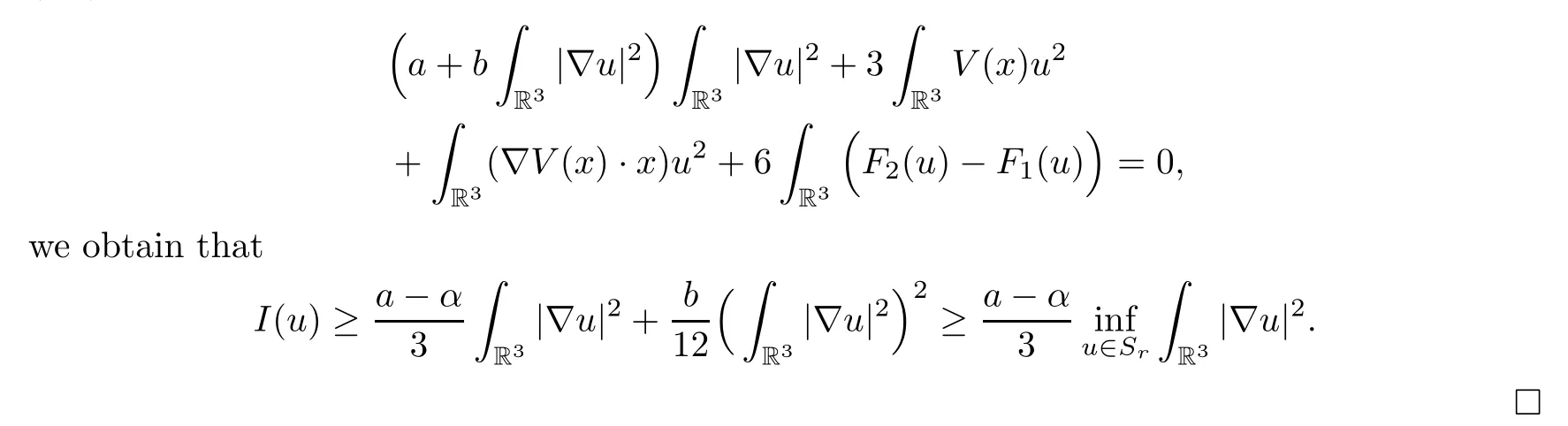
Proof of Theorem 1.2Choose a minimizing sequence {un} ⊂SrwithBy an argument used in the proof of Theorem 1.1,we show that {un} is bounded inFrom Lemma 2.5,there existsu∈such thatun→uin.Hence,the conclusion follows by Lemma 2.7. □

3 The Nonexistence Result

In this section,under the assumptions (V1)(V2)(V4)(V5) and (f1)–(f4),we give the nonexistence result for the problem (1.1).

For our purposes,we need to consider the following problem:

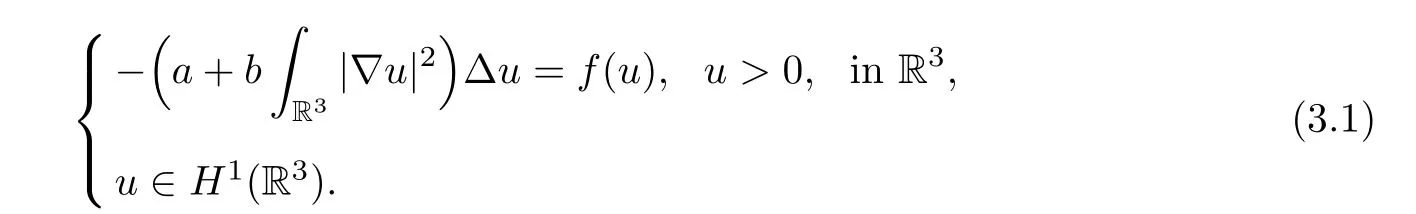
The functionalI∞associated with (3.1) is given by

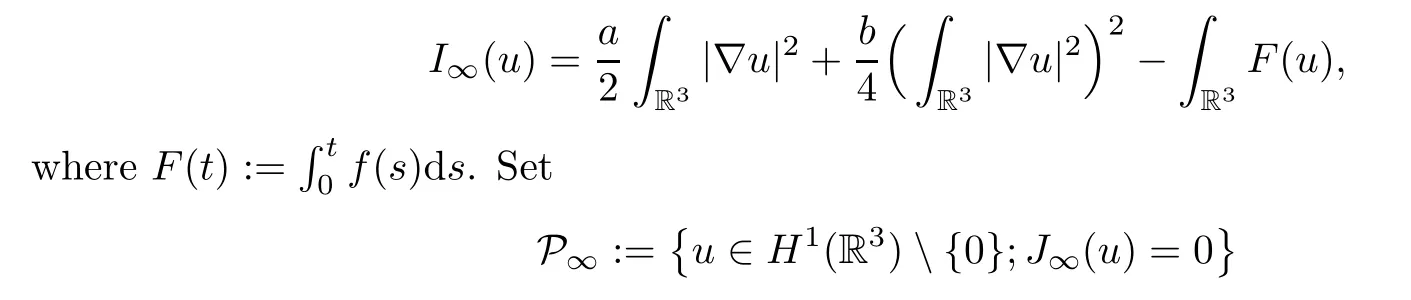
as the Pohozaev manifold related to (3.1) with

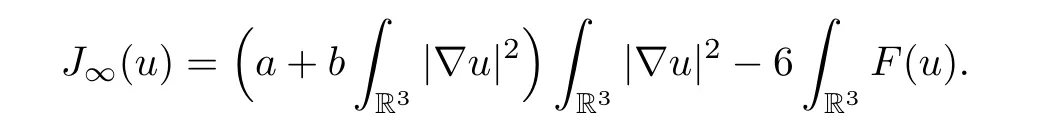
The functionalIassociated with (1.1) is given by

ProofFor anyu∈P,we have that

The assumptions (V5) and (f1)–(f4),along with the Sobolev embedding inequality,imply that

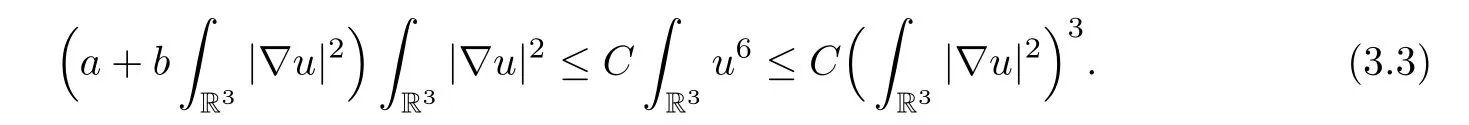
Therefore,there exists a positive constantδ ＞0 such that.From (3.2) and(V4),we obtain that

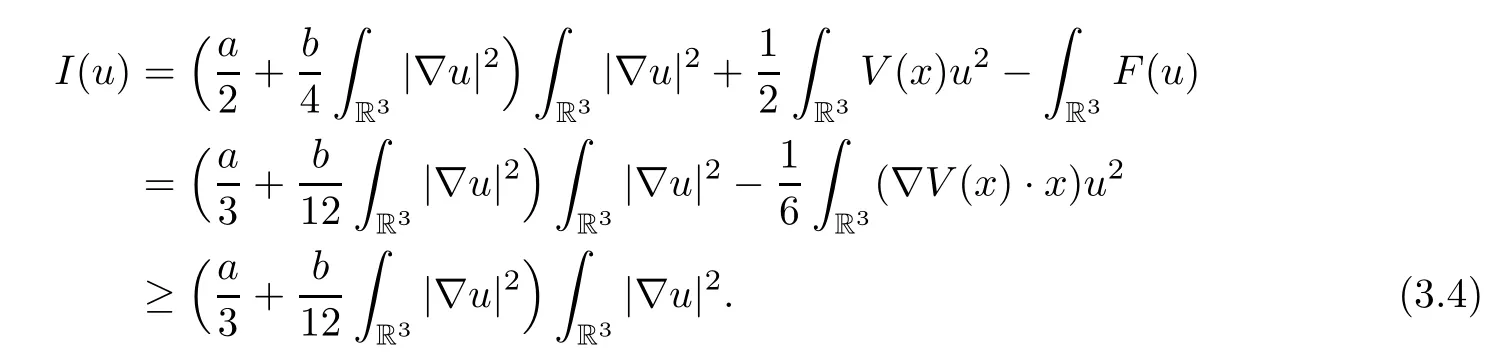
Collecting the previous estimates (3.3) and (3.4),we get that.Similarly,we have that□

Lemma 3.2Letu∈H1(R3) be such that.Then there exists a uniqueθ1∈(0.1] such that∈P∞.In particular,by (V5),the conclusion,for anyu∈P withθ1＜1,holds.

ProofFirst we define the function

According to (f1)–(f4),we have thatψ′(θ)＞0 forθ ＞0 is sufficiently small and ifθ ＞0 is sufficiently large,soψ′(θ)＜0.Sinceψ′is continuous,there exist a uniqueθ1=θ1(u)＞0 such thatψ′(θ1)=0,which means that

Foru∈P,we have that

ThereforeR3F(u)＞0,by (V5).Letθ1＞0 such thatψ′(θ1)=0.Combining (V5),(3.5) and the equalityψ′(θ1)=0,we get that

Thereforeθ1∈(0,1),and the conclusion holds. □

Lemma 3.3For everyu∈P∞,there existssuch thatI∞() ≤I∞(u).

ProofIfu∈P∞,then

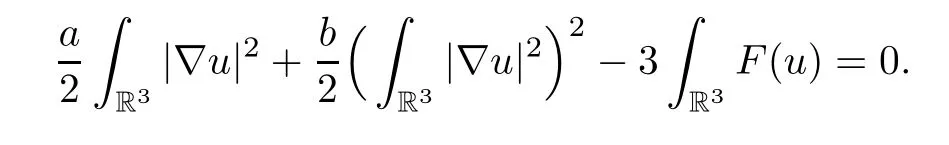
Denote byu*the Schwarz symmetrization ofu.According to the theory of symmetrization,it holds that

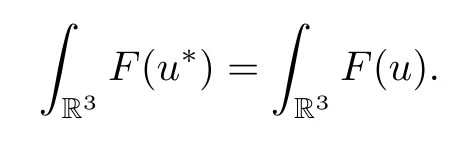
By Lemma 3.2,there existsθ∈(0,1] such that.Therefore,we have that

Applying Lemma 2.4,we have thatun→0 inH1(R3),which contradicts the fact that.This contradiction verifies the claim.

Lettingn→+∞in (3.6),we obtain that

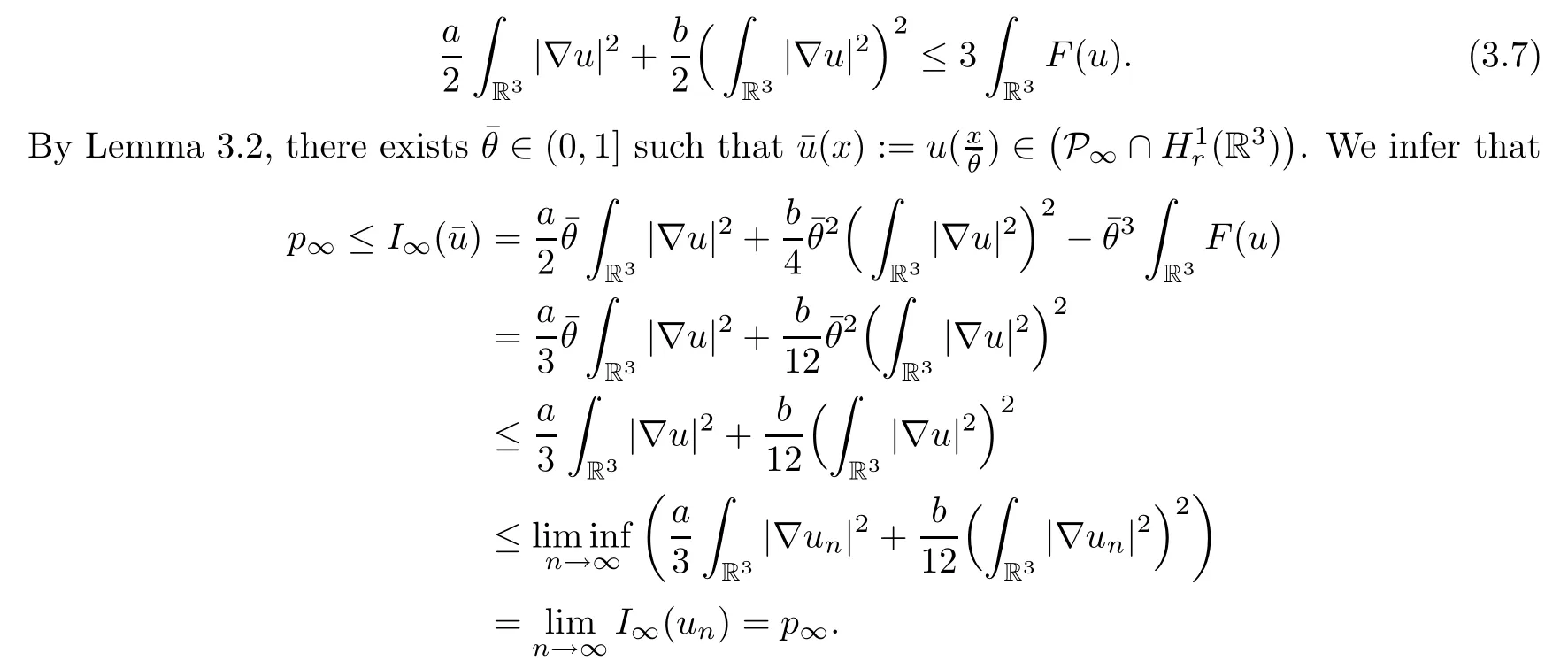
This implies thatI∞()=p∞.□

Lemma 3.5P∞:=｛u∈H1(R3) {0};J∞(u)=0｝is a natural constraint forI∞associated to problem (3.1).

ProofLetube a critical point of the functionalI∞restricted to the manifold P∞.By the theorem of the Lagrange multipliers,there existsμ∈R such that

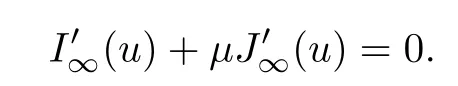
Thus,proving this Lemma is equivalent to proving thatμ=0.Indeed,

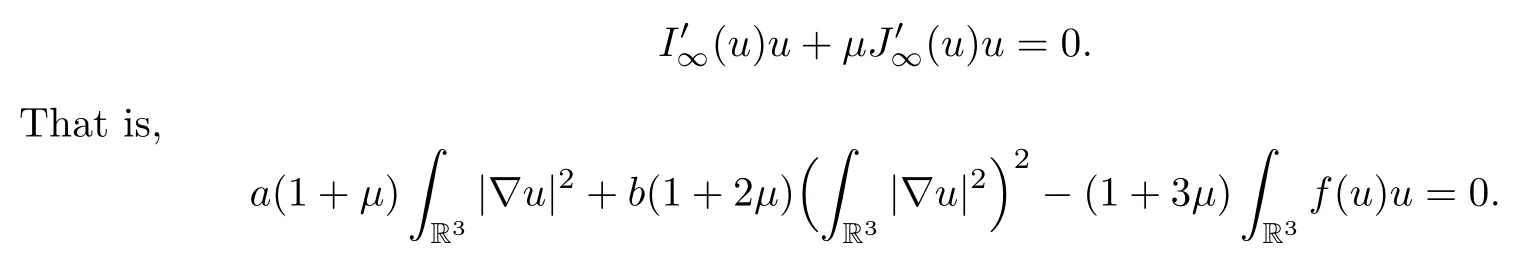
This expression may be associated with the equation

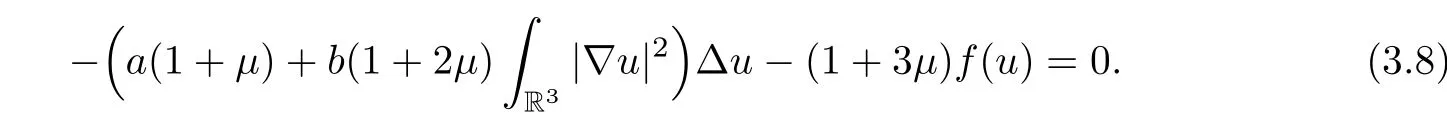
Moreover,solutions of the equation (3.8) satisfy the following Pohozaev identity:

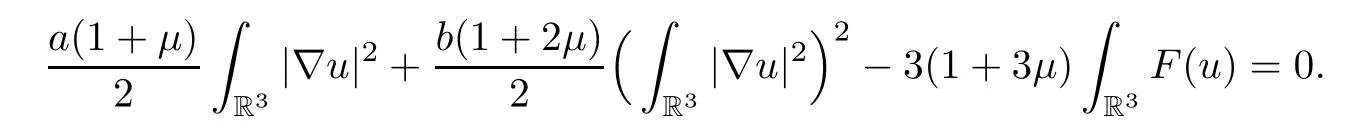
Noting thatu∈P∞,it holds that

Sinceuis a solution of (3.8),(u)=0.This shows that

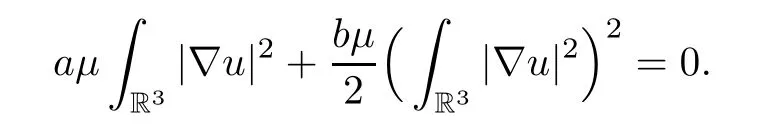
We get thatμ=0,due to the fact thatu≠0. □

Theorem 3.6Assume that (f1)–(f4) hold.Then the problem (3.1) has a positive ground state.

ProofDue to Lemma 3.1,Lemma 3.4 and Lemma 3.5,we obtain a nontrivial solutionu∈H1(R3) to problem (3.1).According to Lemma 3.3,the minimizeruforp∞is radially symmetric and a ground state of (3.1).Notice that |u| ∈H1(R3) is also a ground state of (3.1),since the functionalI∞is even and the manifold P∞is symmetric,hence we may assume thatu≥0.The strong maximum principle and standard arguments [18,19] imply thatu ＞0 in R3.Therefore,uis a positive ground state of problem (3.1). □

Lemma 3.7p≥p∞.

ProofLetu∈P.From Lemma 3.2,there existsθ∈(0,1) such that.By(V4),we have that

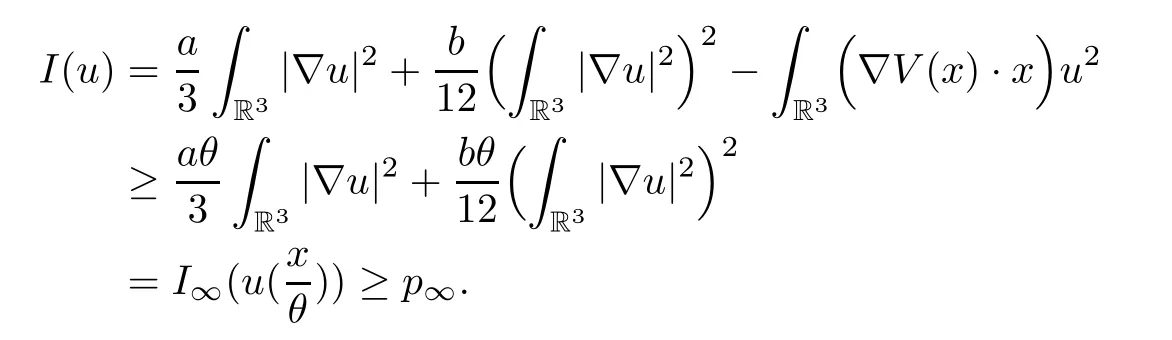
Thus,we obtain thatp≥p∞. □

Lemma 3.8Ifu∈P∞,then there existsθ2＞0 such that∈P.Moreover,we haveθ2∈(1,+∞).

ProofIfu∈P∞,then

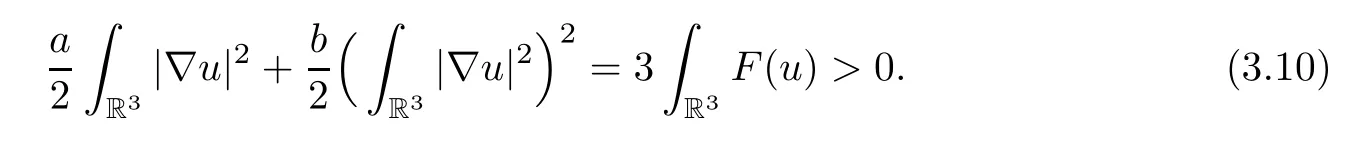
We define the function

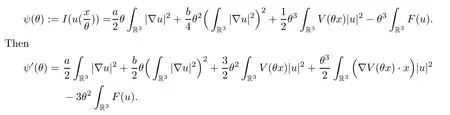
According to (V1)–(V2) and Hardy’s inequality,we have thatψ′(θ)＞0 forθ ＞0 sufficiently small and

Therefore,we conclude thatθ2＞1. □

We conclude that {θyn} is bounded.

Note thatu∈P∞;that is,

From (3.12),(3.13) and (3.14),letting |yn| →+∞,we obtain that

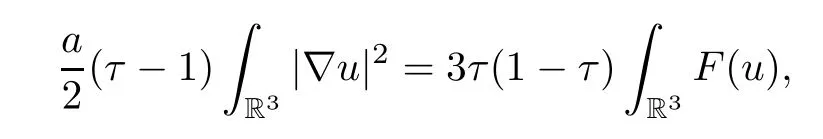
which is impossible,sinceτ ＞1.Hence we get that□

Lemma 3.10p=p∞.

ProofLetw∈H1(R3) be a ground state solution of problem (3.1).Thenw∈P∞,and.For anyy∈R3,we have thatw(· -y) ∈P∞andI∞(w(· -y))=p∞.By Lemma 3.9,there existsθy＞1 such that∈P.Therefore,we have that

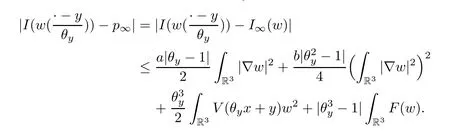
Furthermore,by (V1) and the Lebesgue Dominated Convergence Theorem,we get that

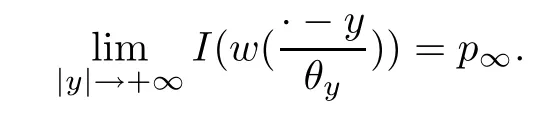
This implies thatp≤p∞.From Lemma 3.7,we havep=p∞. □

Proof of Theorem 1.3Suppose,by contradiction,that there existsu∈H1(R3) such thatu∈P andI(u)=p.By Lemma 3.2,we have thatu() ∈P∞withθ∈(0,1),so

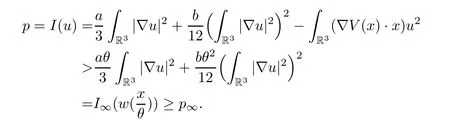
This gives us a contradiction.Therefore the infimumpis not achieved. □