GENERALIZED ORLICZ-TYPE SLICE SPACES,EXTRAPOLATION AND APPLICATIONS*

School of Mathematics and Statistics,Chongqing Three Gorges University,Chongqing 404100,China

E-mail: haiyansongbai@163.com

Abstract We introduce a class of generalized Orlicz-type Auscher–Mourgoglou slice space,which is a special case of the Wiener amalgam.We prove versions of the Rubio de Francia extrapolation theorem in this space.As a consequence,we obtain the boundedness results for several classical operators,such as the Calderón–Zygmund operator,the Marcinkiewicz integrals,the Bochner–Riesz means and the Riesz potential,as well as variational inequalities for differential operators and singular integrals.As an application,we obtain global regularity estimates for solutions of non-divergence elliptic equations on generalized Orlicz-type slice spaces if the coefficient matrix is symmetric,uniformly elliptic and has a small (δ,R)-BMO norm for some positive numbers δ and R.

Key words generalized Orlicz space;extrapolation;Hardy–Littlewood maximal operator;Muckenhoupt weight;variation inequality

1 Introduction

The slice space studied in this paper is associated with the classical Lebesgue space and the generalized Orlicz space.We first give a short history of the generalized Orlicz space.The classical Orlicz spaces are well known and have been studied for a long time,see,for instance the monograph [63] and related references.Generalized Orlicz spaces,also called Musielak–Orlicz spaces and Nakano spaces,are a class of Banach function space that includes a number of spaces of interest in harmonic analysis and PDEs as special cases.The basic example of a variable exponent space was introduced by Orlicz [61].Following [61],the spaces were introduced by Nakano [59,60] and others and a comprehensive synthesis of this earlier work was presented by Musielak [58].As mentioned in [38],generalized Orlicz spaces are of interest as the natural generalization of important function spaces such as Lebesgue spaces,weighted Lebesgue spaces,classical Orlicz spaces,variable Lebesgue spaces and so on.Generalized Orlicz spaces have appeared in many problems in PDEs and the calculus of variations [9–11,13,27,37,40,43],and also have applications for image processing [1,24,41] and fluid dynamics [66].Meanwhile,generalized Orlicz spaces as underlying spaces are drawing more and more attention from those who are interested in functionals or partial differential equations with non-standard growth increase.In [39,40,42],the authors systematically studied the operators of classical harmonic analysis and generalized Sobolev spaces,and established a very broad theory that unites and extends previous work in the generalized Orlicz setting.We refer to the recent book [38] for more details on this topic.

Amalgam spaces were first introduced by Wiener in 1926;see [67–69].In general,for anyp,q∈(0,∞),the amalgam spaceW(Lp,Lq) is defined by setting

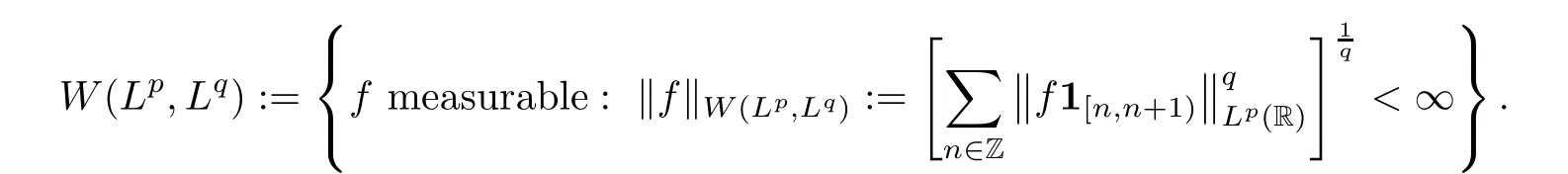
The norm of the element of Wiener amalgam spaces could simultaneously treat localLpand globalLqproperties,while the Lebesgue space does not distinguish between local and global properties.In terms of applications,this makes Wiener amalgam spaces more appealing.In 1980,Feichtinger [31] introduced a generalization of amalgam spaces which enables a vastly wide range of Banach spaces of functions or distributions defined on a locally compact group to be used as local or global components.

Very recently,Auscher and Mourgoglou [7] introduced particular cases of Wiener amalgams,the slice spaces,which are used to study the classification of weak solutions in the natural classes for the boundary value problems of at-independent elliptic system in the upper half-space.In [8],Auscher and Prisuelos–Arribas further introduced a more general slice space,and studied the behavior of operators such as the Hardy–Littlewood maximal operator,the Calderón–Zygmund operators and the Riesz potentials on these spaces.The terminology “slice spaces” comes from the heuristic image of slicing the tent space norm at a fixed height.For more details about slice spaces regarding duality,atomic decomposition and interpolation,we refer to [2].Recall that,for anyq,r,t∈(0,∞),the slice spacein[8] is defined as the space of all locallyr-integrable functionsfon Rnsuch that

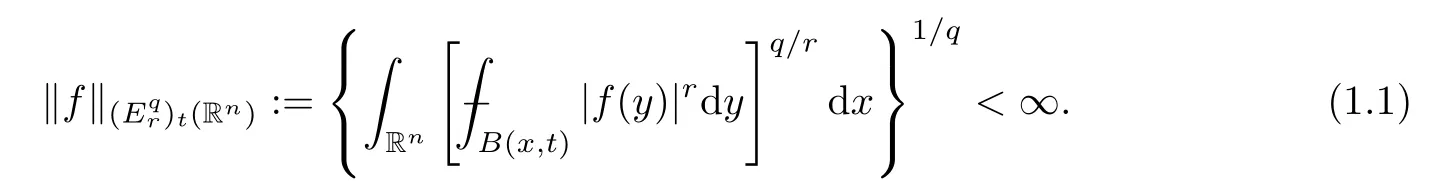
In this paper,we study a new class of slice space,,by replacing the global Lebesgue spaceLq(Rn) in (1.1) with the generalized Orlicz spaceLφ(·)(Rn),which is closely related to the generalized Orlicz tent space(see Definition 7.1 below).

This work is very much influenced by a series of works [6,8,28,29,42].In [8],by establishing the boundedness of some operators on tent spacesand establishing that their slice spacesare retractions of tent spaces,Auscher and Prisuelos–Arribas obtained the boundedness of these operators on.As opposed to the approach in[8],we use an extrapolation result on(see Theorem 3.11 below) to deal with the boundedness of operators,variational inequalities,and the global regularity estimates for solutions of non-divergent elliptic equations on generalized Orlicz slice spaces.As in[28,Theorem 4.6],when one tries to state an extrapolation theorem on a Banach function spaceX,one needs to prove thatX1/q0is a Banach function space and that the Hardy–Littlewood maximal operatorMis bounded on the associate space (X1/q0)′for someq0∈(0,∞).The novelty of this paper is that our extrapolation theorem (see Theorem 3.11 below) ononly needs the boundedness of the Hardy–Littlewood maximal functionMon the generalized Orlicz space,rather than the associate space,whereqandγare positive and real numbers.

The remainder of this paper is organized as follows: in Section 2,we give the necessary definitions and results about generalized Orlicz spaces.In Section 3,we introduce the generalized Orlicz space.To state our extrapolation theorem,we first get the change of angle with theApweights in slice spaces(see Proposition 3.4).In terms of this and the extrapo-

lation result inLφ(·)(Rn) ([29,Theorem 4.5]),we show that for generalized Orlicz slice spaces,at different heightstandswith comparable norms.In addition,we obtain the boundedness of the Hardy–Littlewood maximal operatorMonBy clarifying the relationship between,we establish a version of the extrapolation theorem on generalized Orlicz-type slice spaces (see Theorem 3.11 below).

In Section 4,we apply our extrapolation theorem (see Theorem 3.11 below) to study the boundedness of some classical operators,such as the standard Calderón–Zygmund operators,the Marcinkiewicz integrals with the rough kernels,the Bochner–Riesz mean operators and the Riesz potentials on generalized Orlicz-type slice spaces.Variational inequalities for Calderón–Zygmund operators,as well as the standard averaging operators,are obtained on our slice spaces in Section 5.The last application of our extrapolation theorem is given in Section 6,where we exhibit global regularity estimates for solutions of non-divergent elliptic equations,whose coefficient matrixAis symmetric,uniformly elliptic and has a small (δ,R)-BMO norm for someR ＞0 on the generalized Orlicz slice space.

Finally,let us introduce some notation.ByL0(Rn) we denote the set of (Lebesgue) measurable functions on Rn.For any givenx∈RnandR∈(0,∞),letB(x,R) :={y∈Rn:|x-y|＜R}.Given a locally integrable functionfand a setEwith finite measure,we setFor any setE,we use1Eto denote its characteristic function.LetFor anyp∈[1,∞],letp′be its conjugate index;that is,p′satisfies 1/p+1/p′=1.We always useCto denote a positive constant;their values may change at each appearance.We also useCα,β,···to denote a positive constant depending on the indicated parametersα,β,···.

2 Generalized Orlicz Spaces

Hereafter,we say that a functionfis almost increasing if there existsL≥1 such that for alls≤t,f(s) ≤Lf(t) and we say that a functionfis almost decreasing if there existsL≥1 such that for alls≤t,f(t) ≤Lf(s).We say thatfis increasing/decreasing forL=1.

Definition 2.1Letφ: [0,∞) →[0,∞] be an increasing function such that,φ(0)=.Such a functionφis called a Φ-prefunction.For a Φprefunction,

(2) if it is left continuous and convex,we say thatφis a convex Φ-function;

The set of weak,convex and strong Φ-functions are denoted by Φw,Φcand Φs,respectively.

From the definition,it follows that Φs⊂Φc⊂Φw.

Definition 2.2Given two functionsφandψon [0,∞),we say that they are equivalent,i.e.,φ≃ψ,if there existsL≥1 such that,for anyt∈[0,∞),φ(t/L) ≤ψ(t) ≤φ(Lt).

While it is common in the literature to work with Φ-functions,it is also convenient to work at times with either a weak or a strong Φ-function.One can do this since every weak Φ-function is equivalent to a strong one;see [40,Proposition 2.3].

Lemma 2.3Every weak Φ-function is equivalent to a strong Φ-function.

For two Φ-(pre)functionsφ≈ψ,if there existsK≥1 such that,for anyt∈[0,∞),K-1φ(t) ≤ψ(t) ≤Kφ(t),we say thatφis doubling if there exists a positive constantAsuch thatφ(2t) ≤Aφ(t) for everyt≥0.For doubling Φ functions,≃and ≈are equivalent.

Definition 2.4Givenφ∈Φw,byφ-1we denote the left-inverse ofφ:

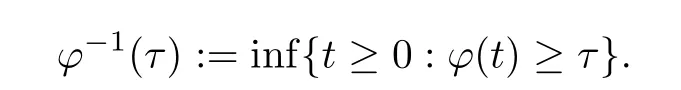
By the definition of the left inverse,we know thatφ-1is increasing and thatφ-1°φ(t) ≤t.Ifφis left-continuous,thenφ°φ-1(τ) ≤τ.

To define generalized Orlicz spaces,we first recall the definition of generalized Φ-functions.

Definition 2.5A functionφ: Rn×[0,∞) →[0,∞) is called a generalized Φ-function if

(1)φ(x,·) is a Φ-function for everyx∈Rn;

(2)φ(x,|f(x)|) is measurable for every measurable functionf(x).The set Φ(Rn) is the family of all generalized Φ-functions.The families Φw(Rn),Φc(Rn) and Φs(Rn) are defined analogously.

Now we recall the generalized Orlicz spaces by referring to [29,Definition 2.6].

Definition 2.6Letφ∈Φw(Rn).For any measurable functionfon Rn,we define the semimodularϱφ(·)by

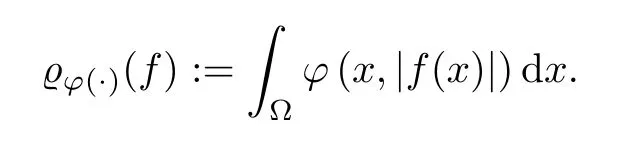
The generalized Orlicz space is defined as the setLφ(·)(Rn):

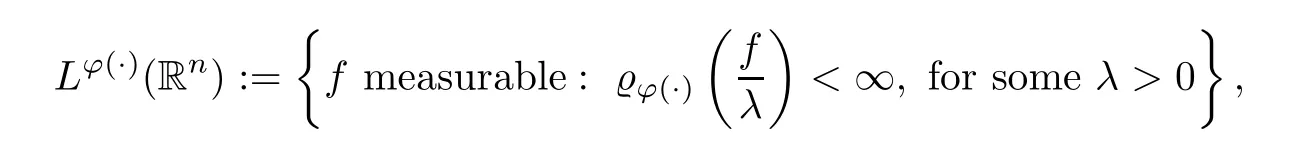
equipped with the (Luxemburg) norm

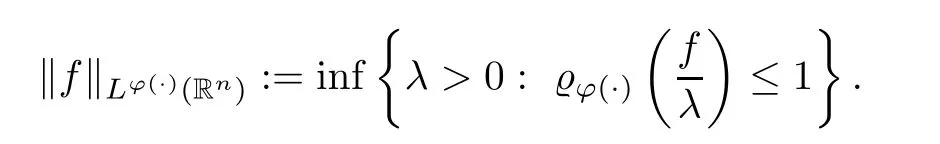
The Hardy–Littlewood maximal operatorMis defined by setting,for any locally integrable functionfandx∈Rn,

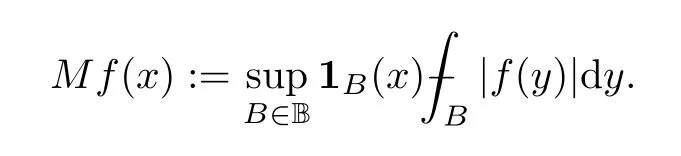
A family of hypotheses for the generalized Orlicz functionφwas introduced in [42] to study the boundedness of the Hardy–Littlewood maximal operatorMon generalized Orilcz spaces.

Definition 2.7Givenφ∈Φw(Rn) and 0＜p ＜∞,we say thatφsatisfies taht

(A0) there existsα∈(0,1] such thatα≤φ-1(x,1) ≤α-1for almostx∈Rn;

(A1) there existsβ∈(0,1) such thatβφ-1(x,t) ≤φ-1(y,t) for everyt∈and everyx,y∈Rnwith |x-y| ≤1;

(A2) for everys ＞0 there existβ∈(0,1] andh∈L1(Rn)∩L∞(Rn) such thatβφ-1(x,t) ≤φ-1(y,t) for almost everyx,y∈Rnand everyt∈[h(x) +h(y),s];

(aInc)pt→t-pφ(x,t) is almost increasing for almostx∈Rn;

(aDec)pt→t-pφ(x,t) is almost decreasing for almost inx∈Rn;

We say thatfsatisfies (aInc) if there existsp ＞1 such thatfsatisfies (aInc)pand (aDec) for somep ＜∞.

Remark 2.8Ifφ∈Φw(Rn) satisfies (aInc)pand (aDec)q,thenp≤q.Indeed,by the definitions of (aInc)pand (aDec)q,we know thatis almost increasing for allx∈Rnand thatis almost decreasing for allx∈Rn.Then,fors,t∈(0,∞) withs ＜t,we have that

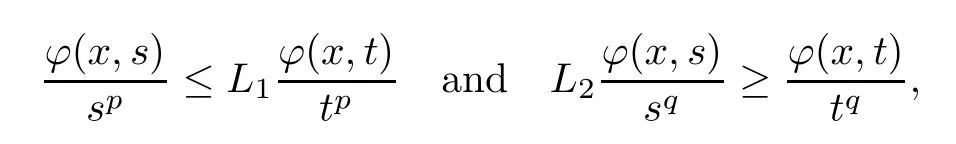
whereL1,L2∈[1,∞).Ifq ＜p,then,for alls ＜twitht∈(1,∞),

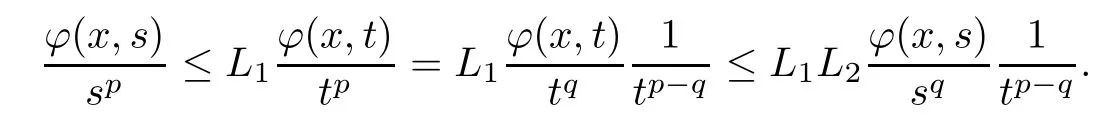
There is a contradiction ast→∞.Thusp≤q.

Remark 2.9Letp∈[1,∞) andφ∈Φw(Rn).Then,

(1) ifφsatisfies (aInc)p,for anyr∈[1,p],φsatisfies (aInc)r.

(2) ifφsatisfies (aDec)p,for anyr∈[p,∞),φsatisfies (aDec)r.

Provided thatφ∈Φw(Rn) satisfies (A0),(A1),(A2) and (aInc),in [42,Theorem 4.7],

Lemma 2.10Letφ∈Φw(Rn) satisfy (A0),(A1),(A2) and (aInc).Then the Hardy–Littlewood maximal operatorMis bounded onLφ(·)(Rn).

Definition 2.11Letφ∈Φw(Rn).For anyx∈Rnandt∈[0,∞),we define the conjugate Φ-functionφ*by

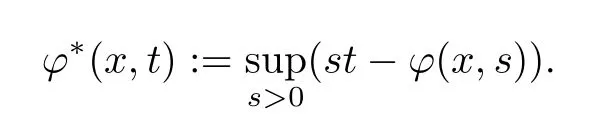
To describe the impact of rescaling and conjugation,Cruz-Uribe and Hst[29] introduced two operators on Φ-functions: givenφ∈Φwandα∈(0,∞),let

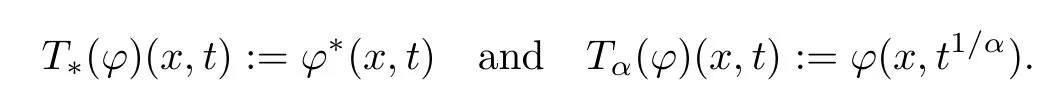
They also proved the following properties:

Lemma 2.12Letφ∈Φwandα∈(0,∞).Then,

(1) conditions (A0),(A1) and (A2) are invariant underT*andTp;

(2)φsatisfies (aInc)por (aDec)pif and only ifT*(φ)=φ*satisfies (aDec)p′or (aInc)p′,wherep∈(1,∞) and.Furthermore,Tαmaps (aInc)pto (aInc)p/αand (aDec)pto(aDec)p/α.

Corollary 2.13Letq∈[1,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2) and(aDec)q.Then the Hardy–Littlewood maximal operatorMis bounded onLφ*(·)(Rn).

ProofFrom Lemma 2.12,it follows thatφ*satisfies (A0),(A1),(A2) and (aInc)q′.This and Lemma 2.10 yield that the Hardy–Littlewood maximal operatorMis bounded onLφ*(·)(Rn).Hence we get the result. □

A weightωis a positive and locally integrable function on Rn.We say thatω∈Ap(Rn),1＜p ＜∞if it holds that

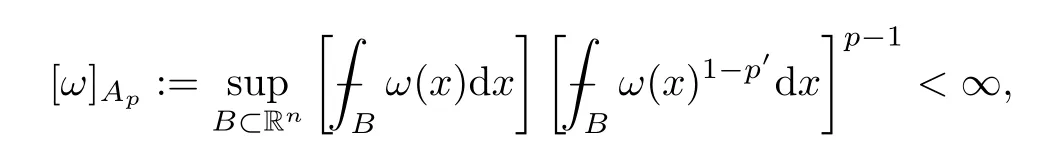
and we say thatω∈A1(Rn) if it holds that

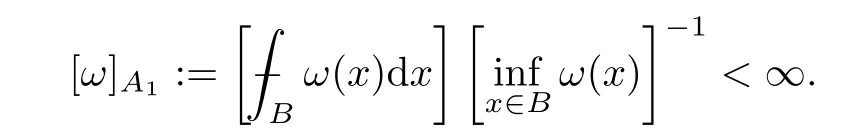
Forp∈[1,∞) andω∈Ap(Rn),we define the weighted Lebesgue spaceLp(Rn,ω) as the set of all measurable functionsfsuch that

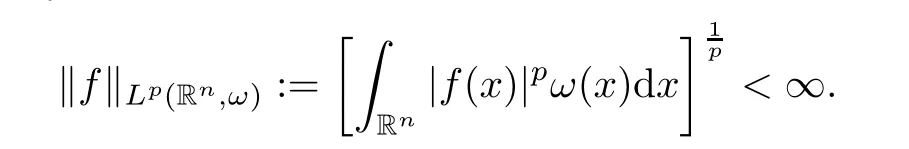
The following extrapolation theorem comes from [29,Theorem 4.5] or [38,Theorem 5.3.1]:

Lemma 2.14Let F be a given family of pairs (f,g) of non-negative and not identically zero measurable functions.Assume that,for somep∈[1,∞) and allω∈A1(Rn),

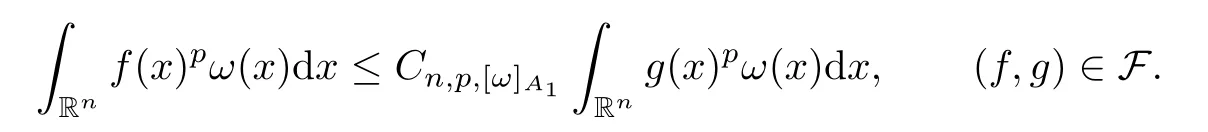
Suppose thatφ∈Φw(Rn) satisfies (aInc)p.If the Hardy–Littlewood maximal operatorMis bounded on,then there exists a positive constantCsuch that

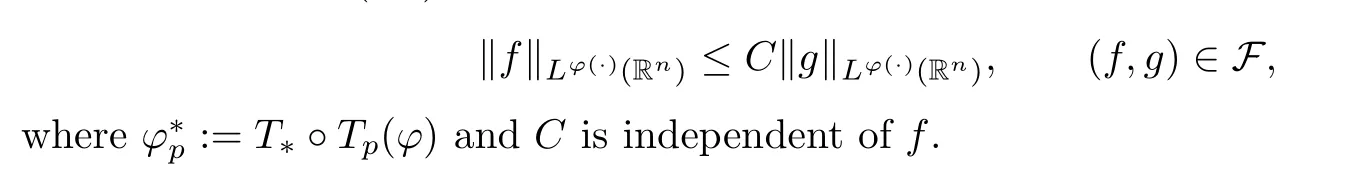
3 Generalized Orlicz-type Slice Spaces

Now we introduce the generalized Orlicz slice space

Definition 3.1Lett,r∈(0,∞) andφ∈Φw(Rn).The generalized Orlicz slice spaceis defined as the set of all measurable functionsfsuch that

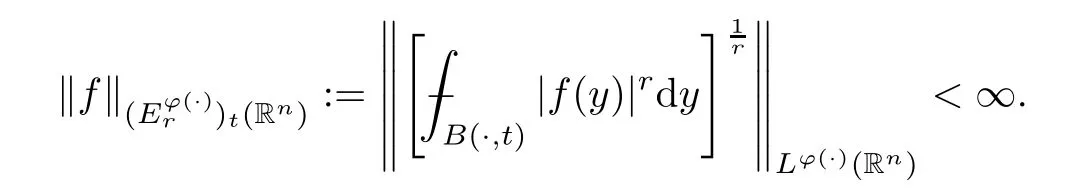
Remark 3.2Letr,p∈(1,∞) andφ(x,t)=tp.goes back to the slice space as in (1.1) introduced in [7] forr=2 and in [8] for the full range ofr.

The following extrapolation theorem on weighted Lebesgue spaces comes from [55,Lemma 3.3]:

Lemma 3.3Let F be a given family of pairs (F,G) of non-negative and not identically zero measurable functions on Rn.Suppose that,for some fixed exponentp0∈[1,∞) and every weightω∈Ap0(Rn),

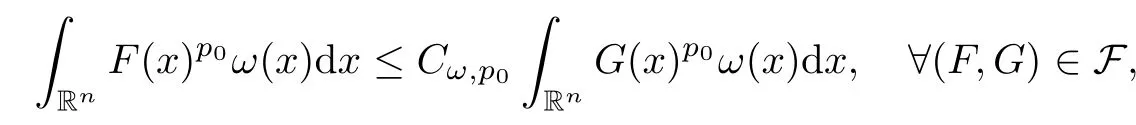
Then,for allp∈(1,∞) and for allω∈Ap(Rn),

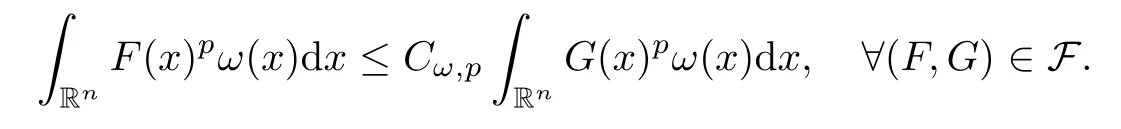
We first apply the above extrapolation theorem to obtain the change of angle withApweights in the slice spaces.More precisely,we state this as follows:

Proposition 3.4Lett∈(0,∞),p∈[1,∞) andα,r∈(1,∞).Givenω∈Ap(Rn) andq∈(0,rp],there exists a positive constantCsuch that

whereCis independent off,tandα.

Remark 3.5Letω≡1,α ＞1,r=2 andq∈(1,∞).Using the fact thatnorms are comparable tonorms with aperturetand [5,Theorem 1.1],the authors in [7,Lemma 3.5] proved that

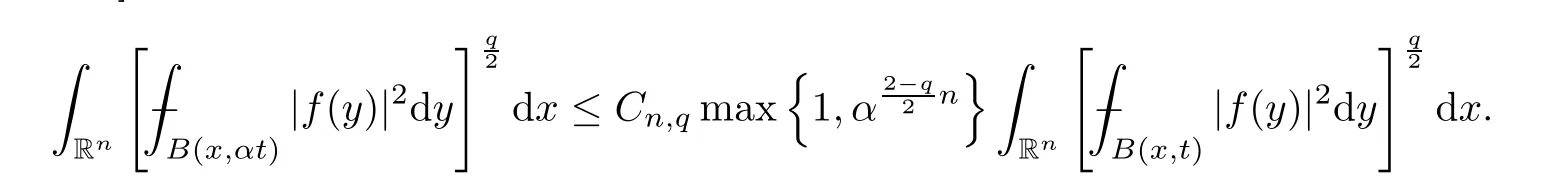
In Proposition 3.4,we do not get the result for the case in whichq ＞2p.

ProofOur idea is motivated by [55].Provided that 1 ≤p ＜∞andω∈Ap(Rn),for every ballBand every measurable setE⊂B,by [36,(7.3)],

To prove Lemma 3.4,we split things to three steps.We first obtain the case in whichq=rand 1 ≤p ＜∞.From this we extrapolate,concluding the desired estimate in the ranges 0＜q≤rpand 1＜p ＜∞.Finally,we shall consider the case in whichp=1 and 0＜q ＜r.

From now on,we fixα ＞1.For the first step,letq=rand 1 ≤p ＜∞.Byω∈Ap(Rn)and (3.1),we conclude that

To prove the second step,take an arbitraryp0∈[1,∞) and consider as F the family of pairs

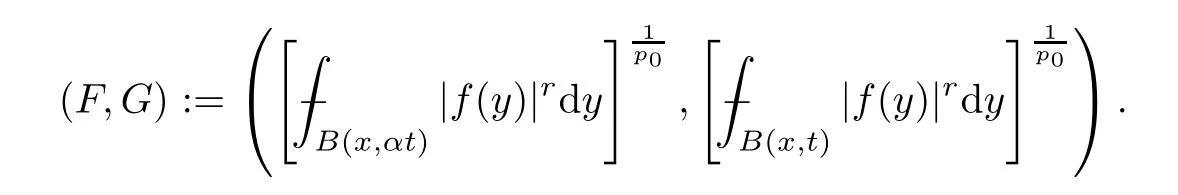
Then,for anyω∈Ap0(Rn),(3.2) gives that

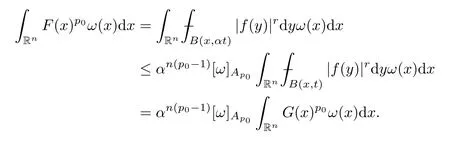
Applying Lemma 3.3,we obtain that,for any given 1＜p ＜∞andω∈Ap(Rn),

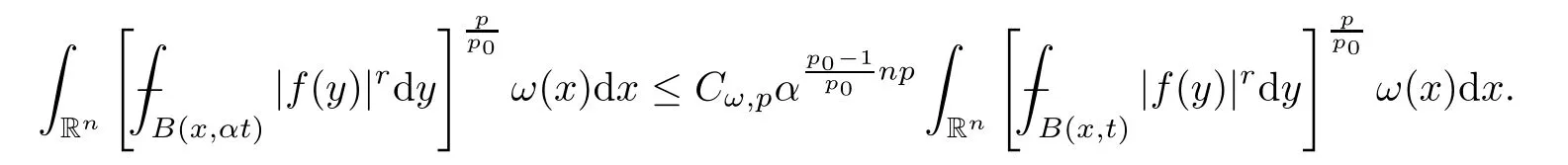
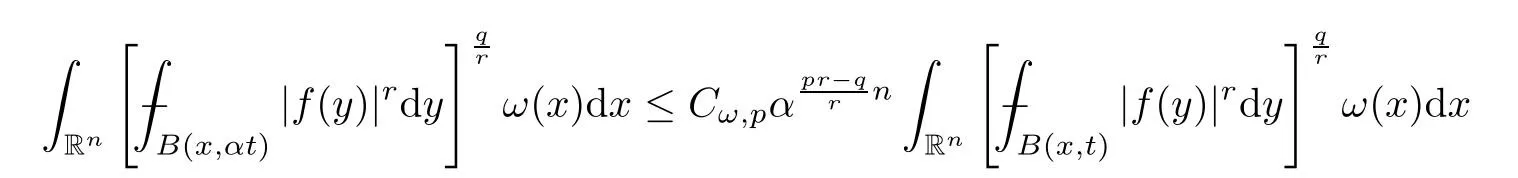
holds true.

To complete the proof it remains to consider the case in whichp=1 and 0＜q ＜r.Without loss of generality,we assume that

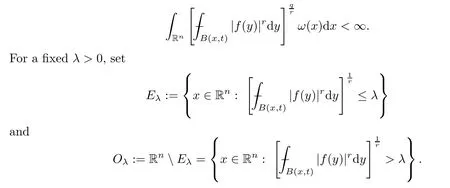
Then,for each 0＜γ ＜1,we also consider the set of globalγ-density with respect toEλdefined by

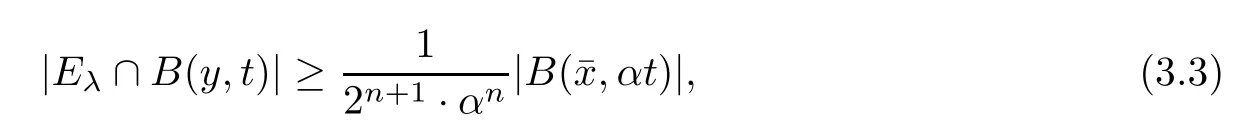
which,together with (3.1),further implies that,for anyy∈R(E*λ),

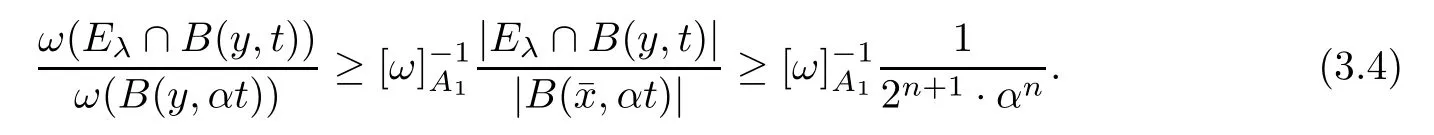
It follows from (3.4) that

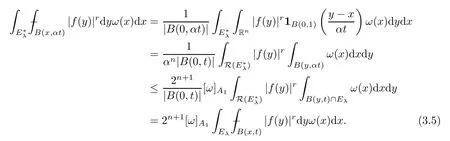
Sinceω∈A1(Rn),by [36,Theorem 7.1],we know thatMis bounded fromL1(Rn,ω) toL1,∞(Rn,ω).From this,(3.3),(3.5) and the definition of,we deduce that

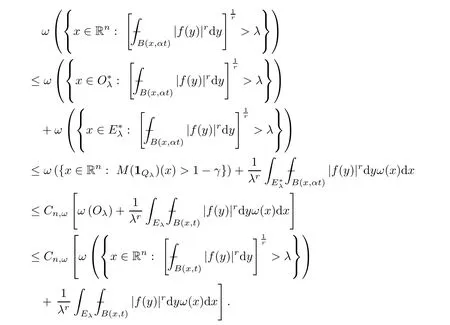
Using this and the assumption that 0＜q ＜r,we obtain that

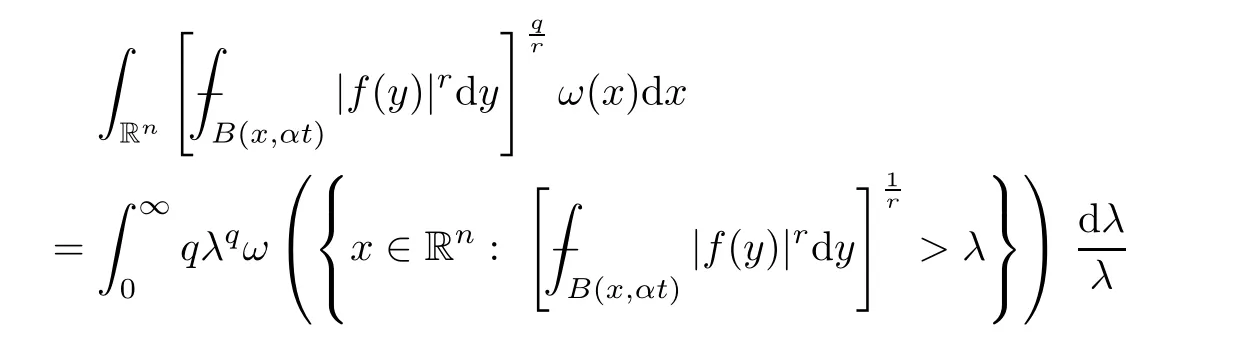
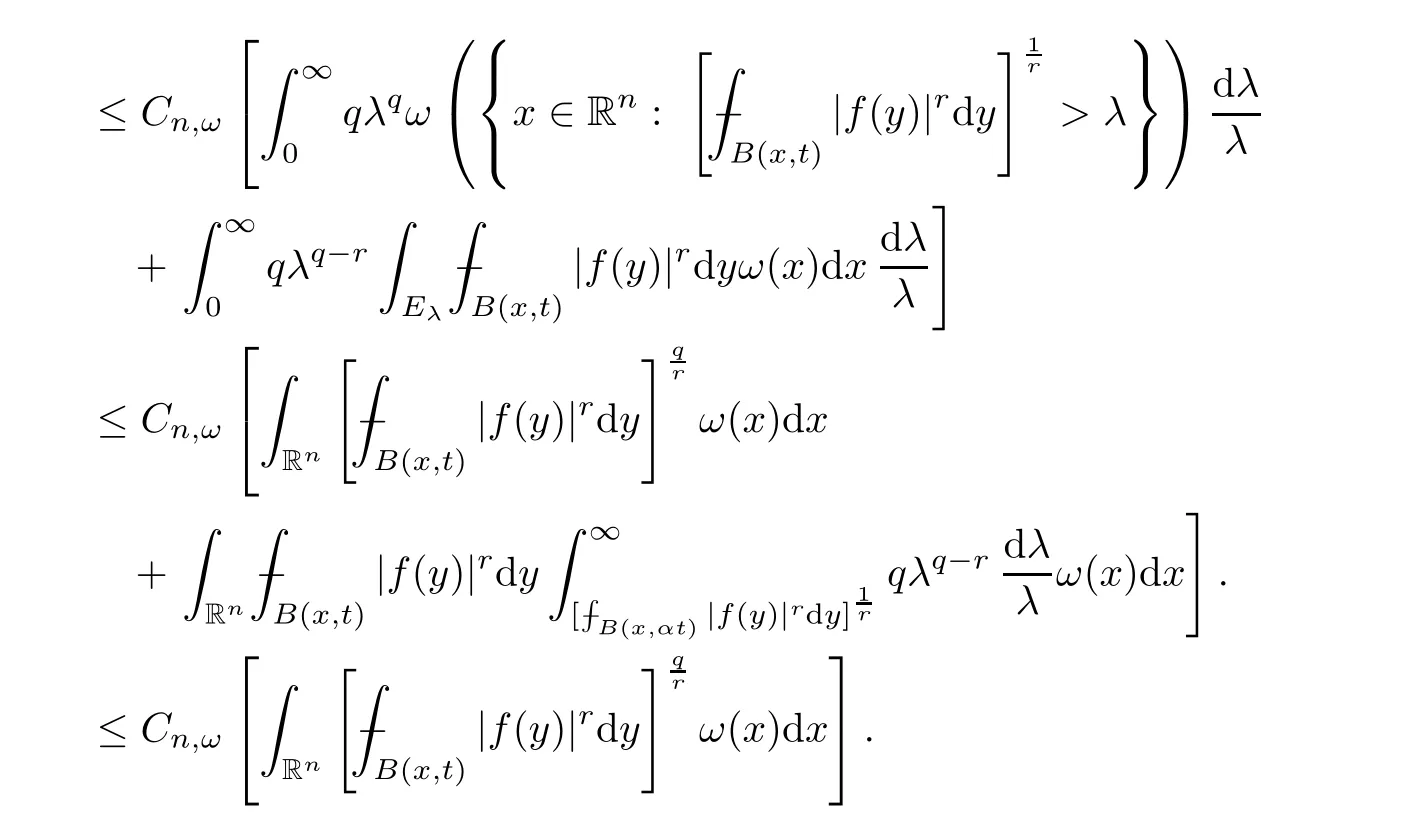
Thus,we have completed the proof of Proposition 3.4. □

Now we use the extrapolation method to show that if a functionfbelongs tofor somet ＞0,then it is also infor alls ＞0.

Theorem 3.6Letr∈(1,∞) and letφ∈Φw(Rn) be a generalized Orlicz function.If there existsq∈(0,r] such thatφsatisfies (aInc)qand the Hardy–Littlewood maximal operatorMis bounded on,then,for anys,t∈(0,∞),with comparable norms.

ProofWithout loss of generality,we assume thats=αtwithα ＞1.Then it suffices to prove that there exists a positive constantCsuch that,for all

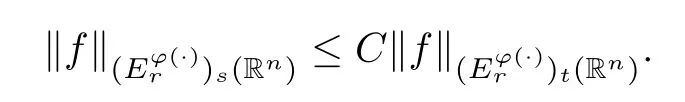
Consider the extrapolation pairs

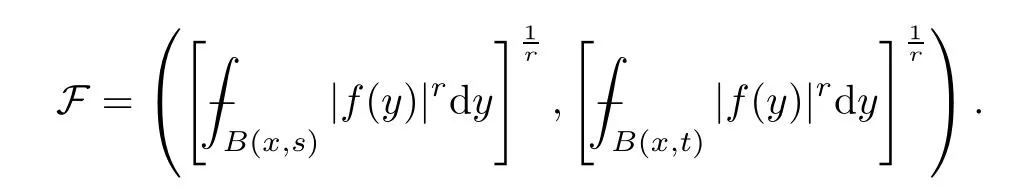
For anyω∈A1(Rn),bys=αt,q∈(0,r] and Proposition 3.4,we have that

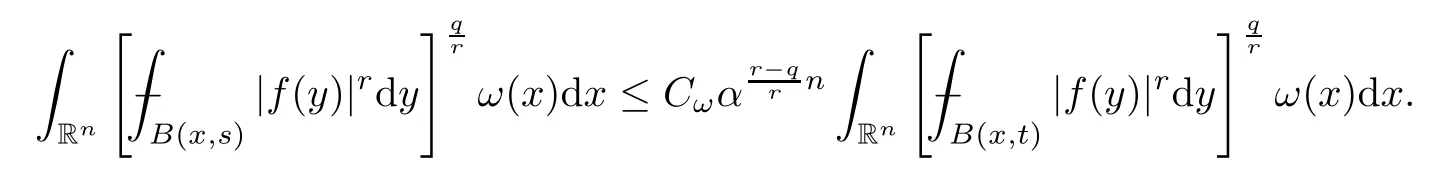
Then,using Lemma 2.14,we conclude that

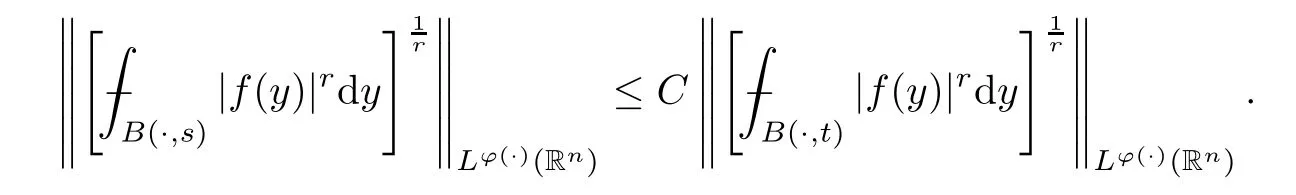
This finishes the proof of Theorem 3.6. □

Next we apply Theorem 3.6 to get the boundedness of the Hardy–Littlewood maximal operator on generalized Orlicz-type slice spaces if it is bounded onfor somep ＞0.

Theorem 3.7Lett∈(0,∞),r∈(1,∞) andφ∈Φw(Rn).If there existsq∈(1,r]such thatφsatisfies (aInc)qand the Hardy–Littlewood maximal operatorMis bounded on,thenMis bounded on;that is,there exists a positive constantCindependent oftsuch that

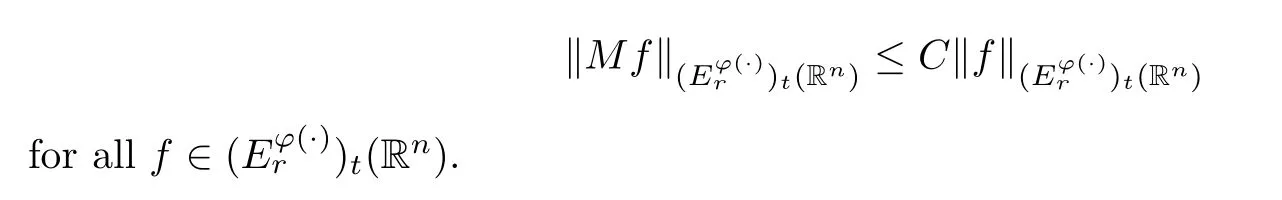
ProofGiven 1＜r ＜∞,by [8,Lemma 4.1],there exists a positive constantCsuch that,for anyt ＞0,x∈Rnand any functionf∈Lrloc(Rn),

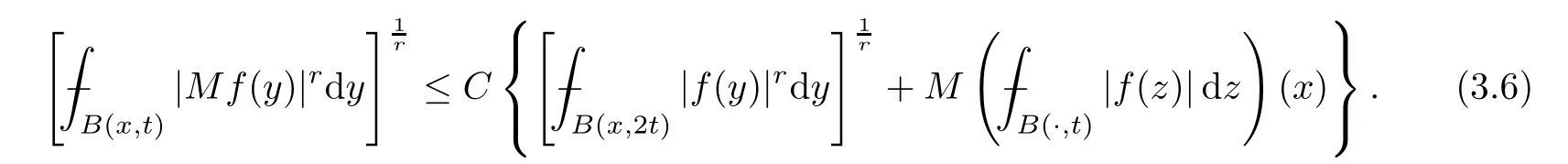
Because ofq∈(1,r] and the assumption thatMis bounded on,in terms of Theorem 3.6,we have that

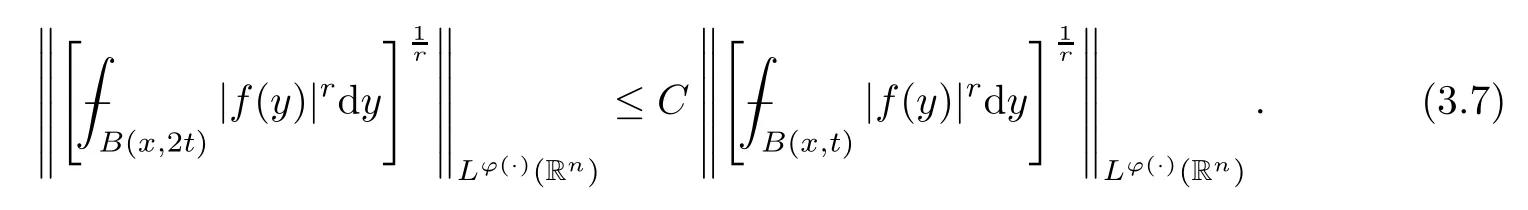
Now we deal with the second term on the right-hand side of (3.6).By [36,Theorem 7.3],for anyq∈(1,∞) andω∈Aq(Rn),

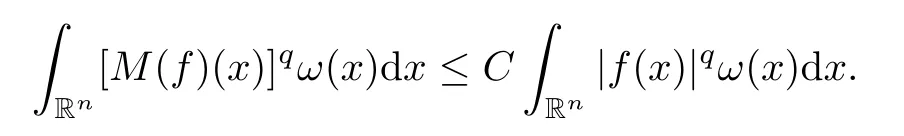
SinceMis bounded on,by Lemma 2.14,Mis also bounded onLφ(·)(Rn).This,together with Hlder’s inequality,yields

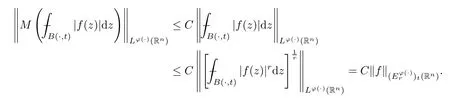
This finishes the proof of Theorem 3.7. □

Corollary 3.8Lett∈(0,∞) andr∈(1,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc) and (aDec).ThenMis bounded onuniformly int.

Definition 3.9Lett,r∈(0,∞) andφ∈Φw(Rn).The associated spaces ofare defined by

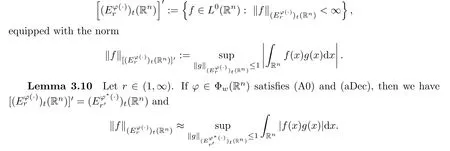
ProofBy Fubini’s theorem,

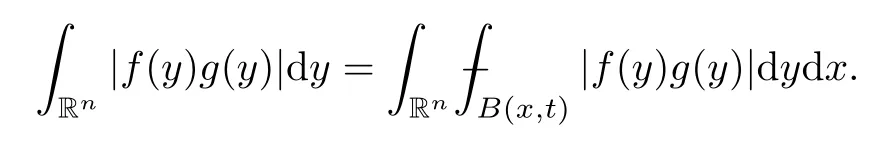
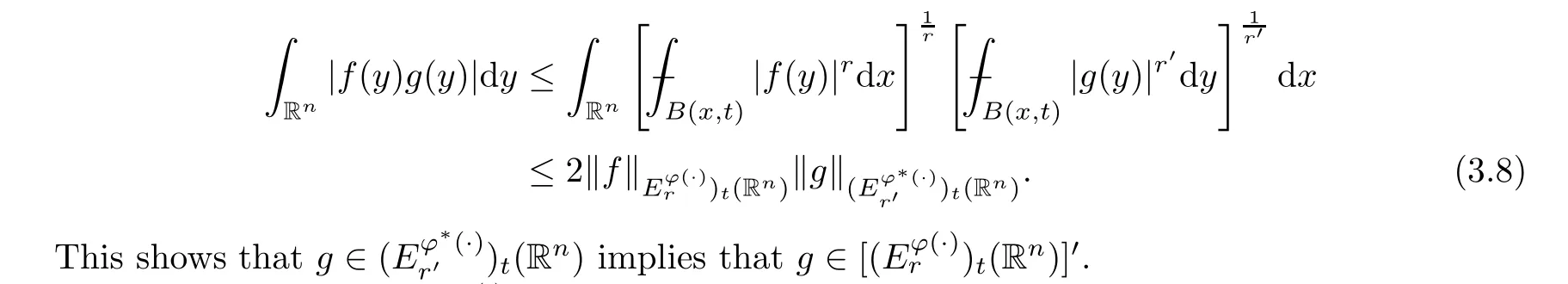
which shows thatgis an element of.Thus,we have completed the proof of Lemma 3.10. □

Now we give a version of the extrapolation theorem on the generalized Orlicz-type slice space.

Theorem 3.11Given a family of extrapolation pairs F,assume that,for somep,q∈[1,∞) withp≤q,and allω∈A1(Rn),

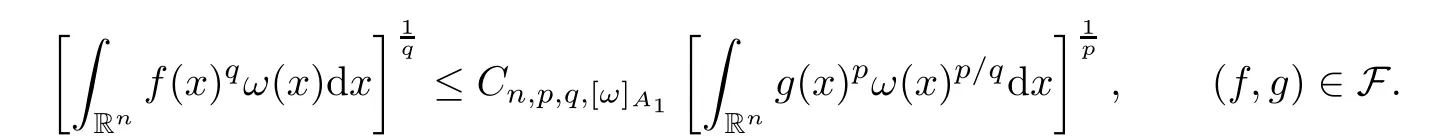
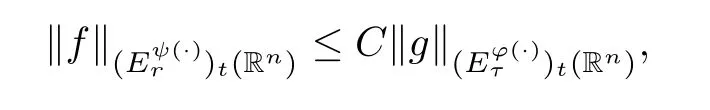
whereCis independent offandt.

ProofSinceτ ＞p,,we have thatr ＞q.By the conditionγ∈(1,(r/q)′] and Theorem 3.7,we conclude thatMis bounded onLetm:=The Rubio de Francia iteration algorithm R :L0(Rn) →[0,∞]is defined by

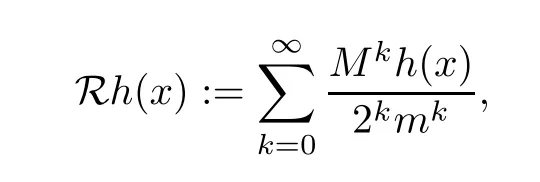
where fork≥1,Mkdenoteskiterations of the maximal operator,andM0h=|h|.The following properties are easily checked by the properties of the maximal functionMand theA1weights:

(A) |h| ≤Rh,

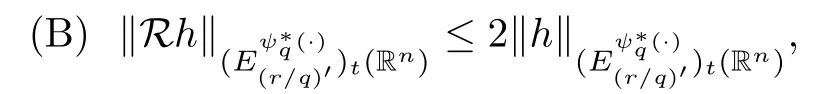
(C) Rh∈A1and [Rh]A1≤2m.

Indeed,|h|=M0(h) ≤Rh,so (A) holds.Using the fact that∞,we have that

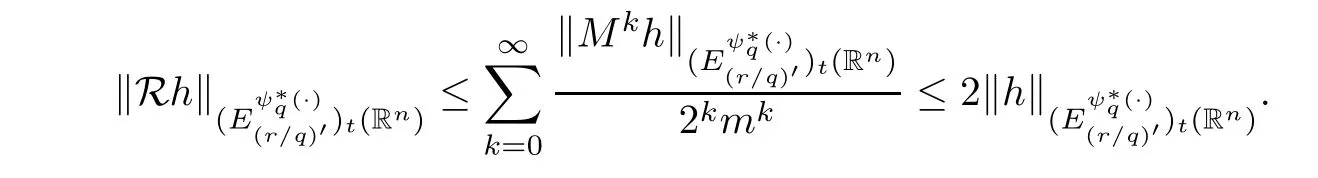
Thus,(B) is valid.Proving (C) is equivalent to proving thatM(Rh)(x) ≤2mRh(x).In fact,for almost everyx∈Rn,by the sublinearity of the maximal operator,

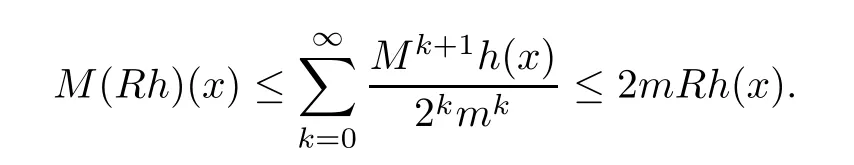
Fix (f,g) ∈F and define.By Lemma 3.10 and (A),we have that

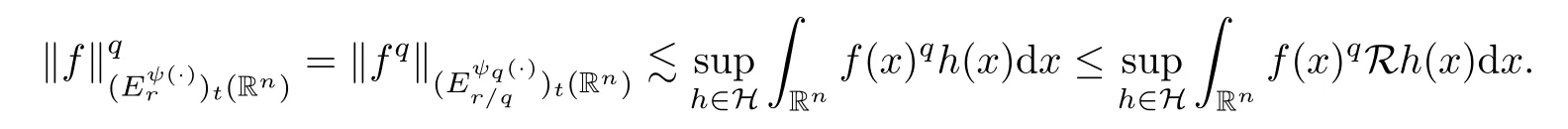
To apply our hypothesis,by our convention of families of extrapolation pairs we need to show that the right-hand term is finite.It follows at once however,by Hlder’s inequality and (B),for allh∈H,

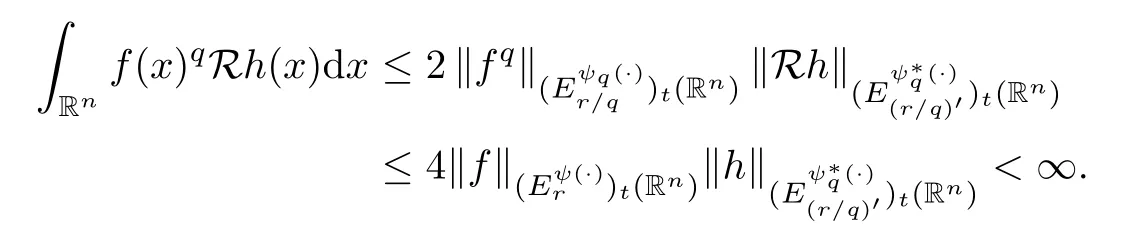
Given this and (C),we can apply our hypothesis to get that

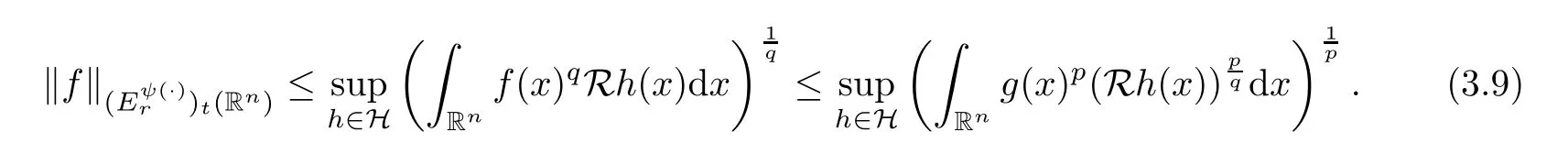
Then,for anyh∈H,by Hlder’s inequality (see (3.8)),we obtain that

It follows from the property (B) that

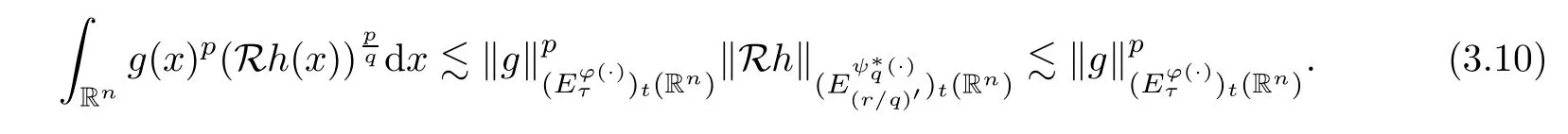
Combined with (3.9) and (3.10),the desired result is concluded. □

Whenβ=0 in Theorem 3.11,we get the following corollary:

Corollary 3.12Given a family of extrapolation pairs F,assume that for somep0∈[1,∞)and allω∈A1(Rn),

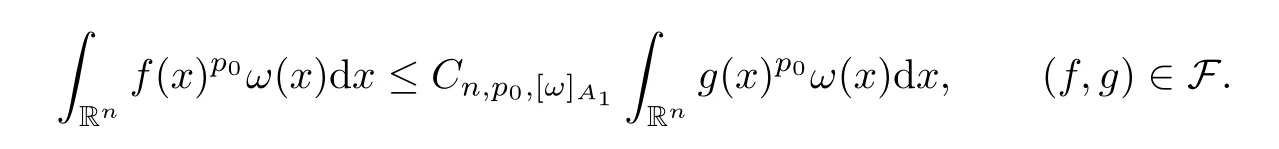
Lett∈(0,∞) andr∈(p0,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(aInc)p0and (aDec).If there existsγ∈(1,(r/p0)′) such that the Hardy–Littlewood maximal operator is bounded on,then there exists a positive constantCsuch that

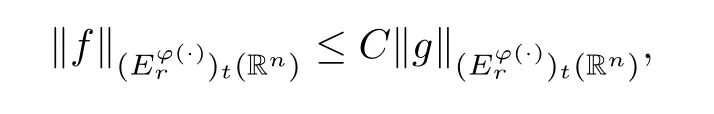
whereCis independent offandt.

Moreover,we have the following corollary:

Corollary 3.13Given a family of extrapolation pairs F,assume that,for somep0∈[1,∞) and allω∈A1(Rn),

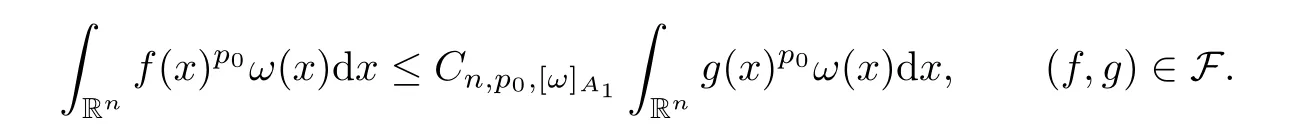
Lett∈(0,∞),r∈(p0,∞) andp∈(p0,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc)pand (aDec).Then there exists a positive constantCsuch that

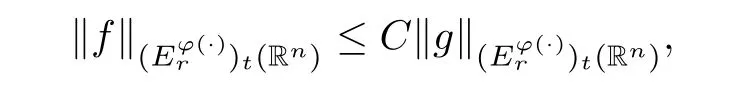
whereCis independent offandt.

ProofSinceφsatisfies (aInc)pand (aDec),there existsq∈[p,∞) such thatφsatisfies (aDec)q.By Lemma 2.12(2),satisfies (aInc)(q/p0)′and (aDec)(p/p0)′.Letγ∈(1,(r/p0)′]such thatγ ＜(q/p0)′.Thensatisfies (aDec)[(q/p0)′/γ]′.Applying Lemma 2.12(1),we know thatsatisfies (A0),(A1) and (A2).From Corollary 2.13,it follows thatMis bounded on,which,together with Theorem 3.11,implies Corollary 3.13. □

Remark 3.14Ausher and Martell [6,Theorem 4.9] proved a limited range extrapolation theorem in weighted Lebesgue spaces.One can also establish a similar version of the limited range extrapolation theorem on the generalized Orlicz slice space;we leave this to interested readers.

4 Boundedness Results for Operators

4.1 The Hardy–Littlewood maximal operator

The vector-valued inequalities for the Hardy–Littlewood maximal operator are very useful for studying function spaces,especially Hardy-type spaces;see,for instance,[64].For 1＜p,q ＜∞,ω∈Ap(Rn) and measurable functions {fk}k∈N,there exists a positive constantCsuch that,for all sequences of {fj}j∈Nsatisfying ‖{fj}‖ℓq∈Lp(Rn,ω),

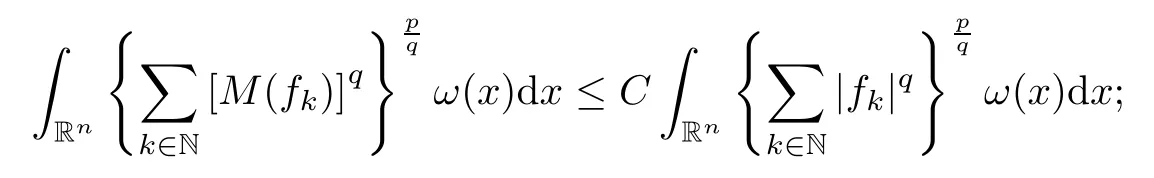
see [4].Therefore,we have the following vector-valued inequality:

Corollary 4.1Lett∈(0,∞) andr∈(1,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc) and (aDec).Then there exists a positive constantCsuch that

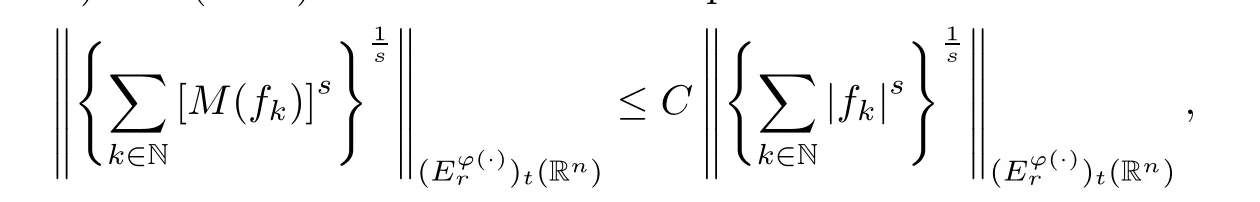
whereCis independent of {fj}j∈Nandt.

4.2 Calderón–Zygmund singular integrals

LetTbe a Calderón–Zygmund singular integral which is defined by,for allf∈andx∈supp(f),

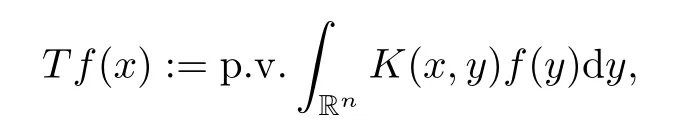
where the kernelK: Rn× Rn{(x,x) :x∈Rn} →R satisfies,for someε ＞0,

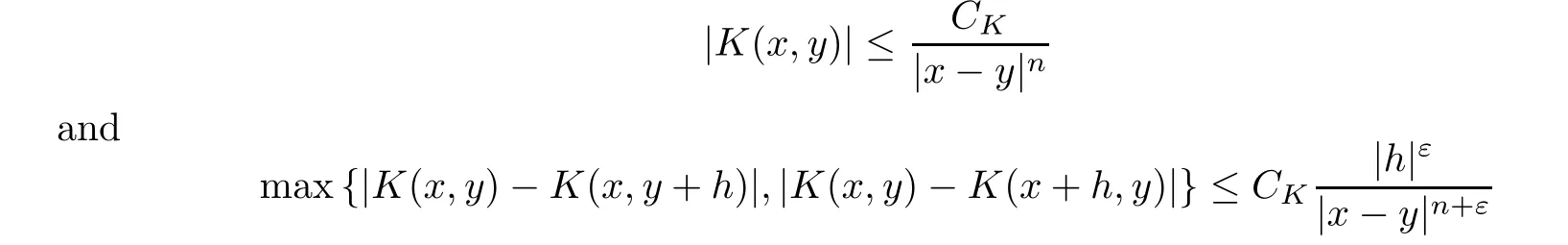
whenever |x-y| ≥2|h|.Moreover,we always assume thatTcan be extended fromL2(Rn)toL2(Rn).From [36,Theorem 7.11],forp∈(1,∞) andω∈Ap(Rn),there exists a positive constantCsuch that,for allf∈Lp(Rn,ω),

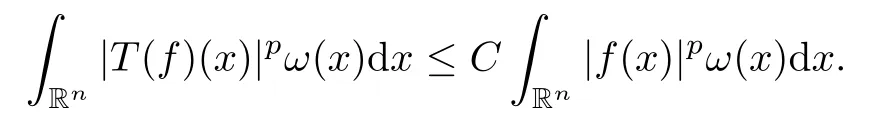
Therefore we have

Corollary 4.2Lett∈(0,∞) andr∈(1,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc) and (aDec).Then there exists a positive constantCsuch that

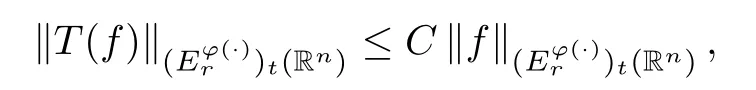
whereCis independent offandt.

4.3 Marcinkiewicz integrals

Letn≥2.We denote by Sn-1the unit sphere in Rnequipped with the normalized Lebesgue measure dσ.Let Ω be homogeneous of degree zero and satisfy that

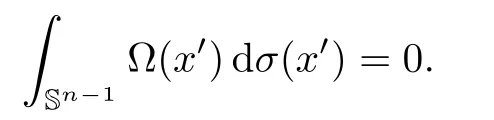
Then the Marcinkiewicz integral of higher dimensionμΩis defined by

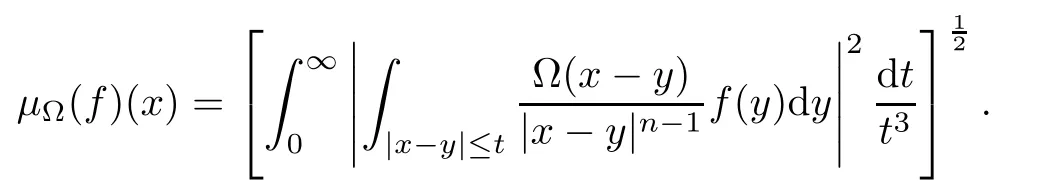
In [33],the authors proved that if Ω ∈Lθ(Sn-1) with 1＜θ≤∞,then,forθ′＜p ＜∞andω∈Ap/θ′(Rn),there exists a positive constantCsuch that,for allf∈Lp(Rn,ω),

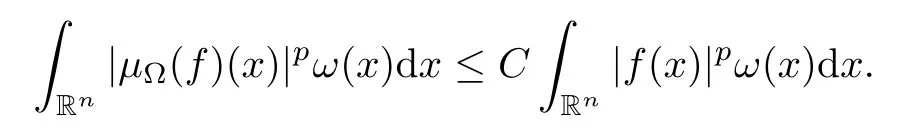
Therefore,we have

Corollary 4.3Let Ω ∈Lθ(Sn-1) with 1＜θ≤∞.Lett∈(0,∞),r∈(θ′,∞) andp∈(θ′,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc)pand (aDec).Then there exists a positive constantCsuch that

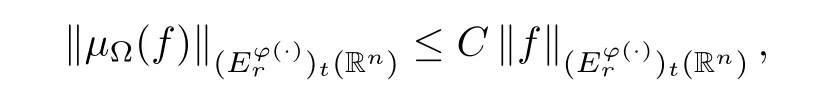
whereCis independent offandt.

4.4 Bochner–Riesz operators

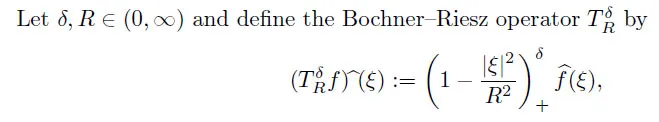
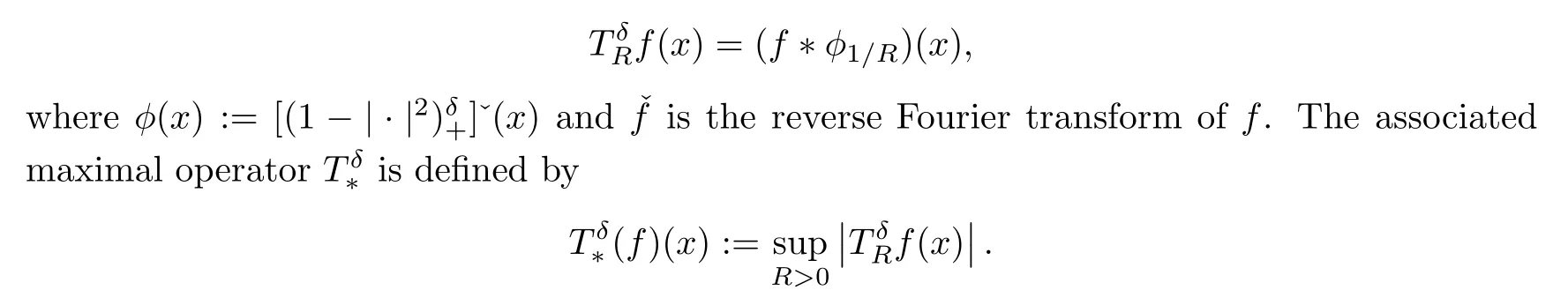
For the case ofn≥2,Shi and Sun [65] proved that ifp∈(1,∞) andω∈Ap(Rn),then there exists a positive constantCsuch that,for allf∈Lp(Rn,ω),

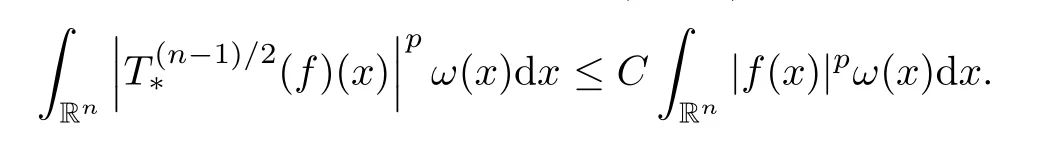
Therefore,we have

Corollary 4.4Letn≥2,t∈(0,∞) andr∈(1,∞).Suppose thatφ∈Φw(Rn) satisfies(A0),(A1),(A2),(aInc) and (aDec).Then there exists a positive constantCsuch that

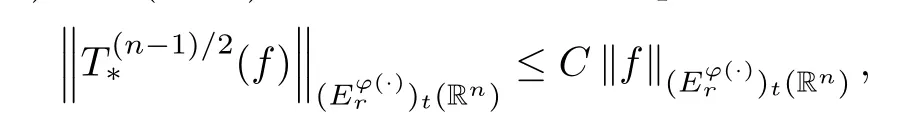
whereCis independent offandt.

4.5 The Riesz potential

Let 0＜α ＜n.The Riesz potential is defined by setting,for almost everyx∈Rn,

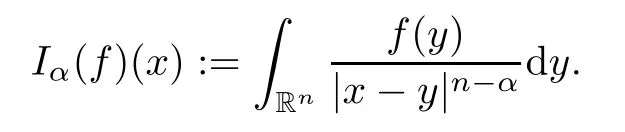
From [57],we can deduce that,for allω∈A1andp,qsuch that 1＜p ＜n/αand 1/p-1/q=α/n,there exists a positive constantCsuch that,for allf∈Lp(Rn,ωp/q),

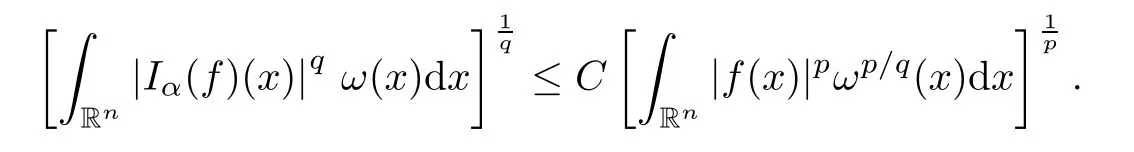
It is known that Muckenhoupt and Wheeden [57] stated the weighted norm inequalities ofIαin terms of the class ofAp,q(Rn).However,as with [29,P.4344],A1(Rn) weights are sufficient for our purpose.

Lemma 4.5Letφ∈Φw(Rn) satisfy (A0),(A1) and (A2).Defineβ∈(0,∞),ψ(x,t) :=[t-βφ-1(x,t)]-1.Thenψalso satisfies (A0),(A1) and (A2).

ProofSincet-βφ-1(x,t) is left-continous and increasing fort,by [38,Lemma 2.3.9(c)and Lemma 2.3.11],we know thatψis increasing,left continuous andψ-1(x,t)=t-βφ-1(x,t).Thusψ-1(x,1)=φ-1(x,1) ≈1 for almost everyx∈Rn,which shows thatψsatisfies the condition (A0).Similarly,we find thatψalso satisfies the condition (A1).

Sinceφsatisfies the condition (A2),for everys ＞0,there existγ∈(0,1] andh∈L1(Rn)∩L∞(Rn) such thatγφ-1(x,t) ≤φ-1(y,t) for almost everyx,y∈Rnand everyt∈[h(x) +h(y),s].Then,for the abovesandγ,

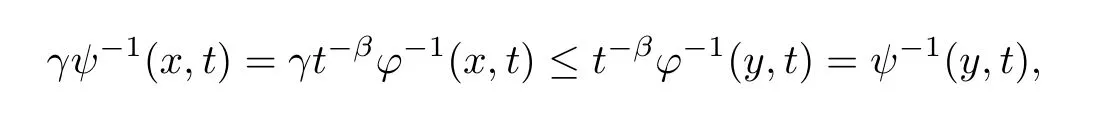
wheneverx,y∈Rnand for everyt∈[h(x) +h(y),s].Thus,we have proven thatψsatisfies(A2). □

Lemma 4.6Letβ∈[0,∞) andφ∈Φw(Rn).Defineψ(x,t) :=[t-βφ-1(x,t)]-1.Let 1 ≤p≤q ＜∞such that.Ifφsatisfies (aInc)p(or (aDec)p),thenψsatisfies (aInc)q(or (aDec)q).

ProofBy similarity,we only prove that ifφsatisfies (aInc)p,thenψsatisfies (aInc)q.From [38,Proposition 2.3.7],we know thatφ-1satisfies (aDec)1/p;that is,there exists a positive constantL∈(0,1] such that,for all 0＜s ＜t,

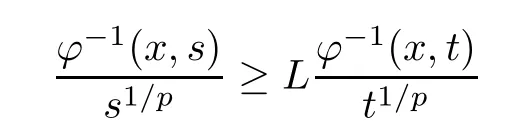
holds true for almost everyx∈Rn.Then,for all 0＜s ＜t,

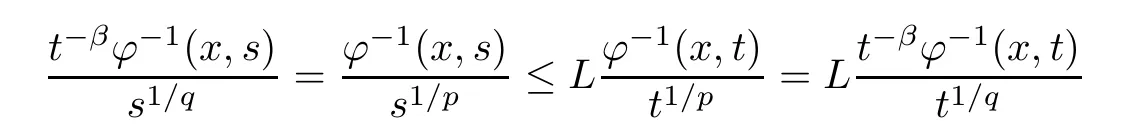
also holds true for almost everyx∈Rn.This shows thatt-βφ-1(x,t) satisfies (aDec)1/q.Applying [38,Proposition 2.3.7] again,we know thatψsatisfies (aInc)q. □

Therefore we have

Corollary 4.7Lett∈(0,∞),r∈(1,∞) and suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc) and (aDec)with 1＜＜n/α.Letψ-1(x,s) :=s-α/nφ-1(x,s),τ∈(1,∞)andr∈(1,∞) withThen there exists a positive constantCsuch that

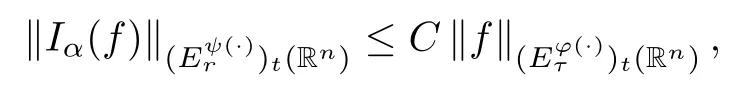
whereCis independent offandt.

5 Variational Inequalities

Variational inequalities have been the subject of numerous recent research articles in probability,ergodic theory and harmonic analysis.The first variation inequality was proven by Lépingle [52] for martingales.Bourgain [12] proved the variational inequality for the ergodic averages of a dynamic system.Bourgain’s work inaugurated a new research direction in ergodic theory and harmonic analysis.Some authors systematically studied jump and variational inequalities for ergodic averages and truncated singular integrals (mainly of homogeneous type);see [21,22,46–49].Very recently,some mathematicians have paid attention to the weighted jump and variational inequalities;see [23,45,53,54] and the references therein for more details.

Let 1 ≤q ＜∞and leta={at}t＞0be be a family of complex numbers.Theq-variation norm of the familyais defined by

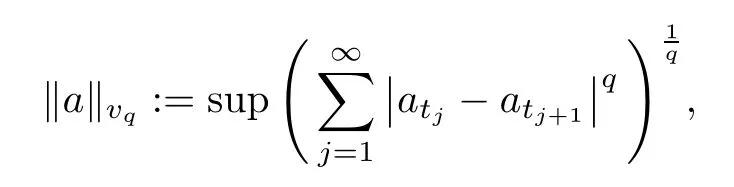
where the supremum takes over all increasing sequences {tj} of positive numbers.All functions on (0,∞) with finiteq-variation are collected as a vector space and denoted byvq.This is a Banach space modulo constant functions.The norm ‖·‖vqwill be also denoted by Vq: Vq(a)=‖a‖vq.

Givenq≥1 and a family of Lebesgue measurable functions F :={Fs:s ＞0} defined on Rn,the strongq-variation function Vq(F) is defined by setting,for anyx∈Rn,

Moreover,given a family of operators A={As:s ＞0} onLp(Rn)(1 ≤p ＜∞),the strongq-variation operator V(A) is similarly defined by setting,for anyf∈Lp(Rn) andx∈Rn,

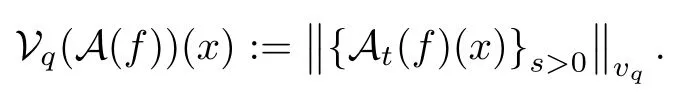
LetKbe a standard Calderón–Zygmund kernel as in Subsection 4.2.For anys ＞0,letKsbe the truncated operator

Set K :={Ks:s ＞0} andq ＞2.By [53,Theorem 1.1],for any 1＜p ＜∞andω∈Ap,there exists a positive constantCsuch that,for allf∈Lp(Rn,ω),

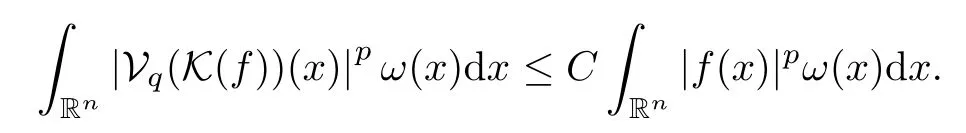
Corollary 5.1Letq ＞2,t∈(0,∞) andr∈(1,∞).Assume thatφ∈Φw(Rn) satisfies(A0),(A1),(A2),(aInc) and (aDec).Then there exists a positive constantCsuch that

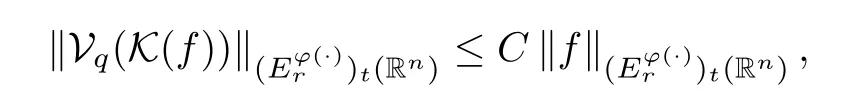
whereCis independent offandt.

Given a locally integrable functionfon Rn,for anyx∈Rnands ＞0,define the average operatorAsas

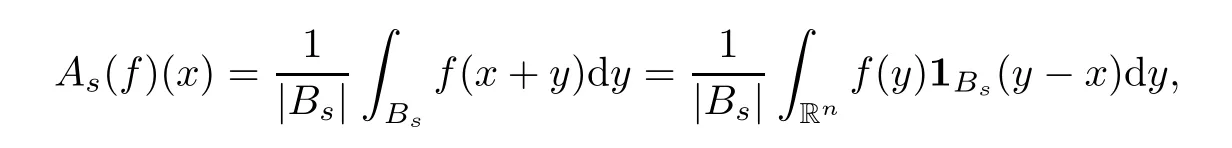
whereBsis the open ball inRnwith the center at the origin and radiuss.Let A={As:s ＞0}.From [53,Theorem 1.2],whenq ＞2,for any 1＜p ＜∞andω∈Ap,there exists a positive constantCsuch that,for allf∈Lp(Rn,ω),

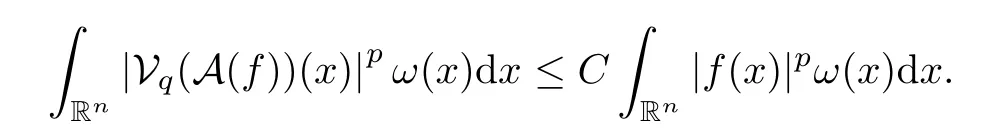
Corollary 5.2Letq ＞2,t∈(0,∞),r∈(1,∞),and letφ∈Φw(Rn) satisfy (A0),(A1),(A2),(aInc) and (aDec).Then there exists a positive constantCsuch that

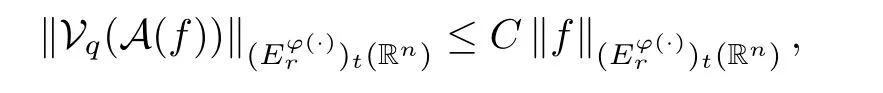
whereCis independent offandt.

6 Global Regularity Estimates for Non-Divergence Elliptic Equations

Consider the elliptic equation in non-divergence form

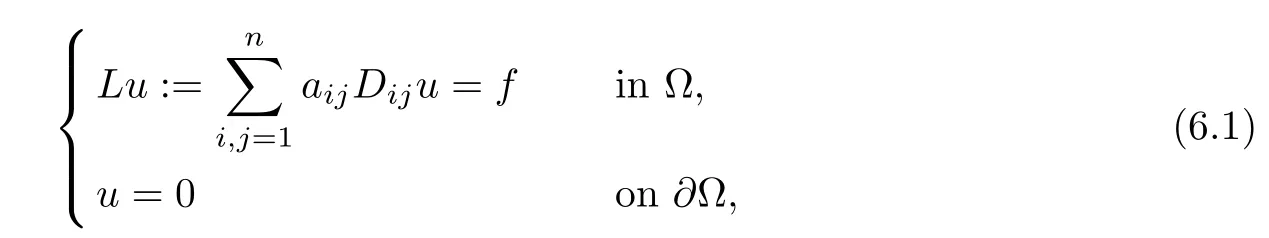
where Ω is aC1,1domain on Rnand the coefficient matrixsatisfies the following conditions:

· (Symmetric condition)aij=ajifor alli,j=1,···,n;

· (Uniformly elliptic condition) there exists Λ＞1 such that Λ-1|ξ|2≤〈A(x)ξ,ξ〉 ≤Λ|ξ|2for allξ∈Rnand a.e.x∈Rn.

The problem under consideration has a long history and has received great attention from many mathematicians.The well-posedness of the problem was proved in [56] under suitable conditions on the coefficients and the underlying domain.Since then,there have been a number of papers which have been dedicated to the study of regularity estimates for the solutions to the problem (6.1).Note that,for the classical Lebesgue spaces,this is the starting point of theLp-regularity theory and a crucial corollary of theLpboundedness of the Calderón–Zygmund operators.We refer to [25,26,50,51] for theLp-regularity results concerning this problem.Moreover,theLp-regularity for the quasilinear elliptic equation in non-divergence form was obtained in [62].The regularity estimate for the problem (6.1) on Morrey spaces was considered in [30].The authors of [15,16,34,70] paid attention to the weightedLp-regularity for this problem.Also,these results have been extended to weighted mixed Lebesgue spaces [35]and variable exponent Lebesgue spaces [14,17–19].Very recently,generalized Orlicz regularity estimates for non-divergent parabolic and elliptic equations have been studied in [3,43].

Definition 6.1A locally integrable functionbon Rnis said to be a BMO function if

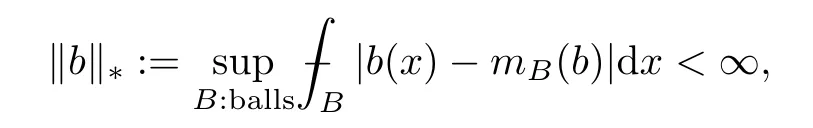
where the supremum is taken over all balls on Rn.

A BMO functionbis said to have a small (δ,R)-BMO norm for someδ ＞0 andR ＞0 if

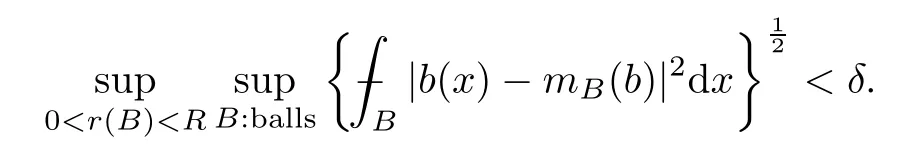
Remark 6.2Clearly,ifbis in BMO(Rn) with ‖b‖*＜δ,then it is (δ,R)-vanishing for everyR ＞0,and ifbis in VMO(Rn) (Vanishing Mean Oscillation),then,for eachδ ＞0,it is(δ,R)-vanishing for someR ＞0.

Now we apply our extrapolation result to obtain a global estimate for solutions of nondivergent elliptic equations on generalized Orlicz-type slice spaces.

Corollary 6.3Let Ω be aC1,1domain,lett∈(0,∞) andr∈(1,∞).Suppose thatφ∈Φw(Rn) satisfies (A0),(A1),(A2),(aInc) and (aDec).Then there exist enough smallδ∈(0,∞) such that the solutionu∈W2,2(Ω) ∩W1,20 (Ω) to the problem (6.1) satisfies the estimate

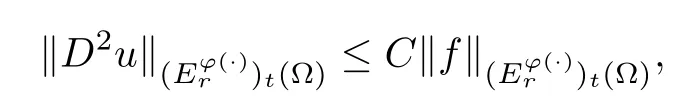
whenever the coefficient matrixAis symmetric,uniformly elliptic and has a small (δ,R)-BMO norm for someR ＞0,whereCis a positive constant independent ofu,fandt.

ProofFrom [15,Theorem 2.4] and [70,Theorem 1.2] (see also [14,Theorem 1.2]),we know that the solutionu∈W2,2(Ω) ∩W1,20 (Ω) of the system (6.1) satisfies that,for anyω∈Ap(Rn) andf∈Lp(Rn,ω) withp∈(1,∞),

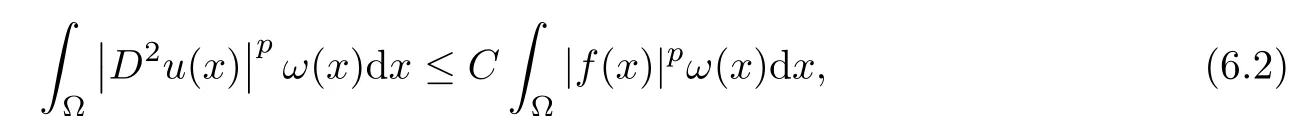
whereCis independent offandu.Sinceφsatisfies (aInc),there existsp∈(1,∞) such thatφsatisfies (aInc)p.Now we can choosep0∈(1,p) such that (6.2) holds trues.By this and by Corollary 3.13,we have that

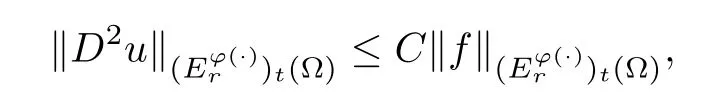
whereCis independent off,uandt.We complete the proof of Corollary 6.3. □

7 Further Remarks

7.1 Generalized Orlicz tent spaces

For anyα∈(0,∞) andx∈Rn,let,which is called the cone of apertureαwith vertexx∈Rn.Letr∈(1,∞).For any measurable functionF:andx∈Rn,define

Recall that a measurable functionFis said to belong to the tent space,withp∈(0,∞),if

Definition 7.1Letφ∈Φw(Rn).The generalized Orlicz tent space,with apertureα,is defined as the set of all measurable functionsFsuch that A(α)(F) ∈Lφ(·)(Rn),and it is naturally equipped with the norm

We have trivial embedding and projection that allow us to carry the properties of generalized Orlicz tent spaces to generalized Orlicz slice spaces by retraction.Letf: Rn:→C.For anyt∈(0,∞),define

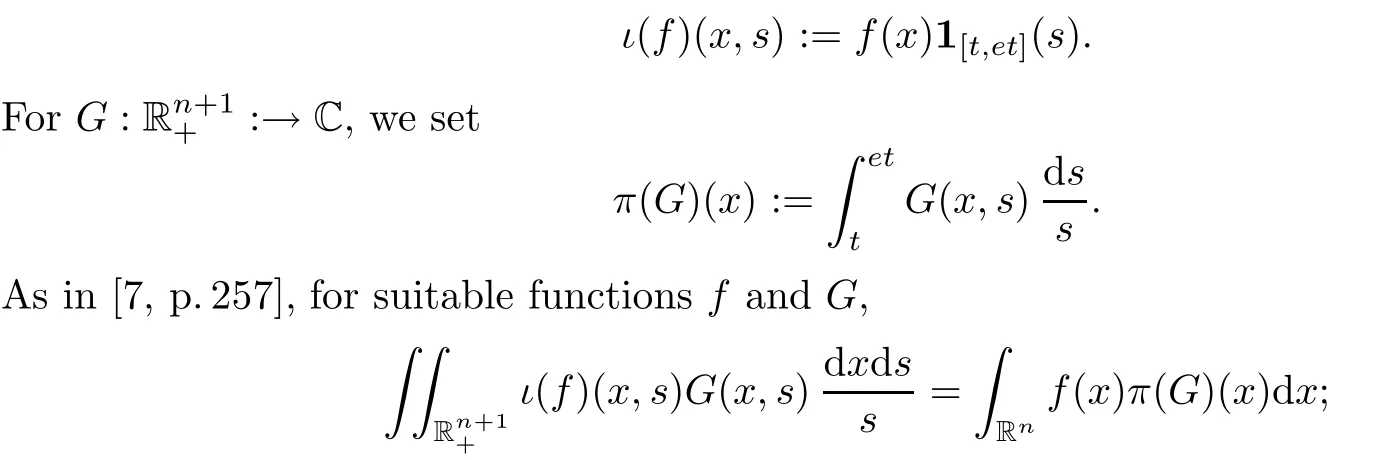
that is,πis the dual ofιin some sense,and

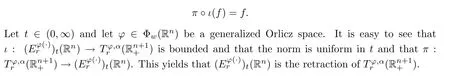
7.2 Hardy-type spaces

Recall that,in [64],the authors developed a real-variable theory of Hardy spaces associated with ball quasi-Banach function spaces;unifies most of the results on Hardy spaces built on different function spaces,such as Hardy spaces,Hardy–Morrey spaces,weighted Hardy spaces,Orlicz–Hardy spaces,variable Hardy spaces,Herz–Hardy spaces,Lorentz–Hardy spaces,amalgam Hardy spaces and so on.For details we refer to [64] and the references therein.

Topologize the space S(Rn) by the norms {pN}N∈Ngiven by setting,for anyN∈N andφ∈S(Rn),

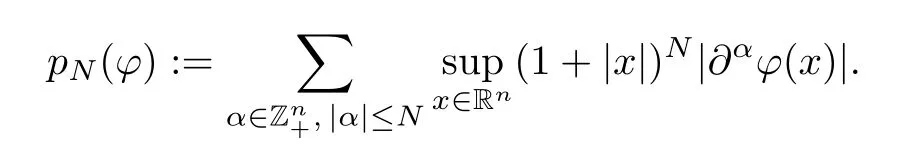
Then,for anyN∈N,define FN:={φ∈S(Rn) :pN(φ) ≤1}.We also endow S′(Rn) with the weak-* topology.

Givenb∈(0,∞) andψ∈S(Rn),define the maximal functionof Peetre type by setting,for allx∈Rn,

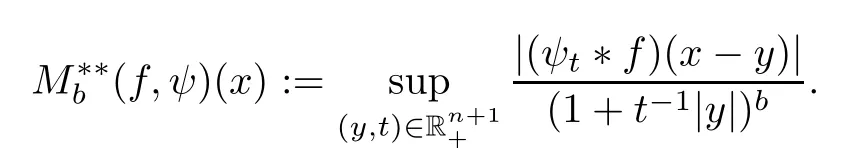
Definition 7.2Lett,r∈(0,∞) andφ∈Φw(Rn).Then we define the Hardy-type spaceas the space of distributions

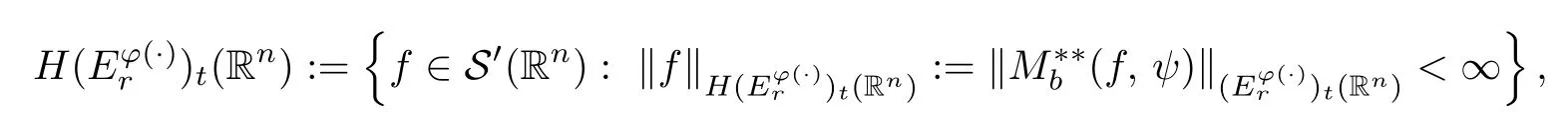
whereb∈(0,∞) is sufficiently large andψ∈S(Rn) satisfies that

Remark 7.3In [71],the authors studied the Orliz-slice Hardy spaceH(EqΦ)t(Rn).However,this is absolutely different from our Hardy-type spaces.

Letφ∈Φw(Rn) satisfy (A0),(A1),(A2) and (aDec).According to [64],the real-variable theory of some Hardy-type spaceHX(Rn) heavily depends on the vector-valued Fefferman–Stein inequality on its underlying function spaceXand properties of the Hardy–Littlewood maximal operatorMon the associated spaceX′.By Corollary 4.1 we have the vector-valued Fefferman–Stein inequality over generalized Orlicz-slice spaces.Applying Lemma 3.10 and Corollary 3.8,we can attempt to obtain some boundedness of the Hardy–Littlewood maximal operatorMon the associated space of generalized Orlicz spaces.Therefore,the real-variable theory of the Hardy-type spacecould be established as a special case of the Hardy-type space in [64].