Development of a methodology for assessing the adequacy of electric power systems

Dmitry S.Krupenev,Denis A.Boyarkin,Dmitrii V.Iakubovskii

1.Melentiev Energy Systems Institute of Siberian Branch of the Russian Academy of Sciences,Lermontov str.,130,Irkutsk,664033,Russia

Abstract: This study presents the results of a research into the developing a methodology for assessing the adequacy of advanced electric power systems characterized by the integration of various innovative technologies,which complicates their analysis.The methodology development is aimed at solving two main problems: 1) increase the adequacy of modeling the processes that occur in the electric power system and 2) enhance the computational efficiency of the adequacy assessment methodology.This study proposes a new mathematical model to minimize the power shortage and enhance the adequacy of modeling the processes.The model considers quadratic power transmission losses and network coefficients.The computational efficiency of the adequacy assessment methodology is enhanced using efficient randomnumber generators to form the calculated states of electric power systems and machine learning methods to assess power shortages and other reliability characteristics in the calculated states.

Keywords: Electric power systems,Adequacy,Power shortage minimization,Pseudo-and quasi-random number generation,Machine learning methods.

0 Introduction

In the context of the operation of electric power systems(EPS),issues with regard to their reliability are becoming increasingly relevant.This relevance is owing to various reasons including the following:

-The growing role of electricity in human lives and the continuously increasing demands of end users for reliable power supply.Recently,there have been an increasing number of cases of significant economic damage as well as damage to human health and life owing to power outages[1-3].The requirements for advanced life support systems such as heat supply,water supply,fire extinguishing,and security to ensure their power supply reliability,are high.This is primarily owing to the service facilities (which are generally crowded locations) and the failure of life support systems (including that owing to electricity nonsupply),which can result in adverse consequences.This is particularly true for life support systems that operate under harsh climatic conditions,where the cost of failure of such systems increases significantly.

-Complications in the management of EPS functioning,long-term operation,and expansion planning.These are primarily owing to the integration of distributed generation[4],renewable energy sources (RES)[5],and energy storage systems[6]into the EPS and the emergence of loadcontrolled consumers[7].These technologies have specific operating conditions that affect EPS reliability and generate the requirement for a more detailed representation of the system.

-Various conventional problems in the electric power industry.These include the high wear and tear of certain energy equipment,low culture of repairs,and low rates of advancement and renovation of energy equipment[8].

The reliability of power systems can be only resolved by using dedicated methods and tools for assessing their reliability.Moreover,the EPS reliability should be assessed in all the periods of the life of the system,and the reliability indices obtained should be used to make decisions to ensure reliability.

This study addresses the adequacy of the EPS.Adequacy is the capability of the EPS to satisfy the requirements of consumers within a certain amount and constraints on the energy resources supply,given unplanned and planned interruptions in the operation of the EPS components and operational constraints[9].Adequacy is considered while solving problems related to long-term planning and the long-term expansion of the EPS.

The reasons listed above actualize the issues of EPS reliability and impose certain requirements on the adequacy assessment methodology.The main requirements are more detailed representation of the EPS structure,enhancement of the accuracy of the EPS modeling processes,and the use of effective mathematical methods and digital technologies.Therefore,this study aims to present the results of a study on improving the computational efficiency of the methodology for assessing EPS adequacy.This is necessary for effectively solving various problems in the synthesis of the reliability of the power supply.This paper comprises the Introduction,four sections,and the conclusions.The first section presents a description of the methodology used for the EPS adequacy assessment.The second section focuses on the results of a study on the influence of pseudo-and quasi-random number generators on the computational efficiency of the methodology for EPS adequacy assessment and experimental studies on the analyzed generators.The third section describes a new model for minimizing the EPS power shortage.It considers the network coefficients and quadratic power losses.The fourth section presents the observations of the application of machine learning methods to the analysis of the calculated states of the EPS.

1 Methodology for assessing EPS adequacy

The problem of EPS adequacy assessment is formulated as follows: determining the adequacy indices for the given hourly power consumption schedules over a certain period for the reliability zones;unit commitment;technical and reliability parameters of the generating equipment in the reliability zones;and the structure,technical,and reliability parameters of power lines in the interzone tie lines.Adequacy is generally assessed considering only the main structure of the EPS (generation and main network),without the distribution network.Power consumers are equivalent at the level of buses of step-down substations with a high voltage of 220 kV (110 kV in certain cases)[10].The widespread development of distributed generation necessitates the factoring in of individual sections of the distribution network with distributed generation for an effective assessment of adequacy.The calculated scheme is represented as a multi-zone model while assessing adequacy.Each zone includes part of the analyzed power system.This system is characterized by a set of generating units and an integrated hourly power consumption schedule for the assessment period.The electrical network within the reliability zone was not considered.This is because it is considered that there cannot be any constraint on active power transmission under any of the most probable conditions.It is noteworthy that when necessary,there can be a separate generating station (generating unit) or substation with the load of a specific consumer in the reliability zone.The power transmission lines (TLs)between reliability zones are considered because these form interzone tie lines,for which the constraints on active power transmission in normal and repair conditions are known in advance.

For the EPS adequacy assessment factors in stochastic events and processes that occur in EPS,the calculated scheme has a large dimension.Only a few of the known reliability assessment methods for technical systems are suitable for solving this problem because we assess an EPS consisting of thousands of components for a sufficiently long time.In practice,a methodology for assessing adequacy relies on the Monte Carlo method[10-12]and involves three main computational steps:

1.Generate the calculated states of the EPS based on the Monte Carlo method.

2.Minimize power shortages in the calculated states of EPS,and determine the power shortages in the EPS reliability zones for each calculated state.

3.Calculate the EPS adequacy indices.The primary indices among these are the probability of shortage-free operation in reliability zones,mathematical expectation of power shortages in reliability zones,and mathematical expectation of power undersupply in reliability zones.

The methodological requirements presented in the introduction determine the lines of development of the adequacy assessment methodology,which is feasible in several directions.This study focuses on the following:1) the use of sequences of numbers distributed uniformly in a normed space at the first computational stage to obtain the fastest feasible convergence of the Monte Carlo method,2) the enhancement of the adequacy of representation of the power shortage minimization problem for EPS and the application of effective mathematical methods for solving it,and 3) the use of machine learning methods to analyze the calculated states of the EPS.

2 Study of the influence of random number generators on the computational efficiency of EPS adequacy assessment methodology

The stage of generating random (calculated) EPS states involves the formation of a set of probable calculated states for the considered period.The calculated states of the EPS were generated for all the hours of the analysis period while simulating random events based on the Monte Carlo method.These events include the failures of generating units,failures of power transmission lines,and irregular load fluctuations.A random event (generator unit failure,power line failure,etc.)kmwith a probability ofpmis simulated by sampling a random numbersmfrom a set with a uniformly distributedSin the interval [0,1].Ifsmlies in the interval[0,pm],kmis considered to have occurred.Otherwise,eventkmdoes not occur.

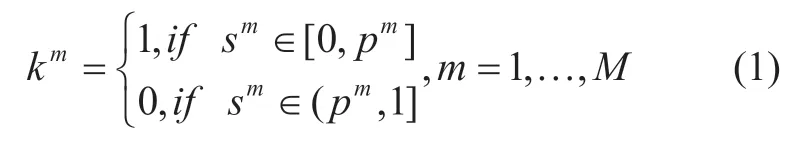
whereMis the set of calculated states of EPS.

The quality of the random numbersSused in the problem is of high importance for the speed and accuracy of adequacy assessment.The characteristic of the distribution of random numbers and the correlation (interdependence) of neighboring values affect the simulation results.Using the Monte Carlo method,sequences of random numbers should satisfy the following fundamental requirements to the extent feasible:

-the most feasible repetition of a random distribution (in particular,a uniform distribution);

-non-availability of correlations in the relative position of the members of the sequence;

-a sufficiently large period of repetition (looping) of the sequence (or the absence of such a period as in “entropy generators”).

Note that it is infeasible to obtain a true random number generator using mathematical modeling.Pseudo-random number generators (PRNGs)[13]and quasi-random number generators (QRNGs)[14]were used to obtain sequences of random numbers.The most commonly used PRNGs are Mersenne Twister[15],Xorshift[16],PCG[17],and their derivatives.QRNGs generate non-random sequences to ensure better uniform distribution properties.These include the Holton[18],Niederreiter[19],and Sobol sequences[14].The algorithms Mersenne Twister and Xorshift are based on a linear feedback shift register,and PCG improves the simplest linear congruential generator by applying an output permutation function.The proposed QRNG algorithms generate low-discrepancy sequences that are distributed uniformly within a unit hypercube.All the algorithms have different properties that affect the results of the calculations and simulations using the Monte Carlo method.However,notwithstanding the availability of various tests for their evaluation (NIST,TEST-U01,DIEHARD,etc.),it is occasionally infeasible to reliably determine the behavior of the system while using these.Therefore,experimental calculations are required.

The indicated pseudo-and quasi-random number generators were tested to assess the adequacy of the EPS test.In addition,a comparative analysis of the performance of the approaches relied on the formula for the calculation error of the Monte Carlo method[19]:

whereζis a random variable modeled by the Monte Carlo method,Dζis the variance of the random valueζ,andNis the number of trials.

Adequacy is assessed by the Monte Carlo method unless the stop criterion is attained,i.e.,the threshold valueξis given a priori.Consequently,two indicators affect the speed of attainment of the threshold value,according to Formula (2):

1) the number of calculated states of EPS,

2) the convergence rate of a random variable,which is characterized by the variance.

Thus,it is necessary to identify a sequence of random numbers at which the maximum rate of convergence of the random variable under study is attained,which corresponds to the minimum number of tests required to achieve specified accuracy.Simultaneously,it is necessary to consider that different periods are required to form different sequences of numbers depending on the complexity of the algorithm.

The testing was performed on IEEE RTS-24[20],as shown in Fig.1(a).While assessing adequacy,the system was divided into reliability zones (Fig.1 (b)),with interzone tie lines consisting of power lines between the reliability zones.Figure 1 (b) shows the controlled cut sets (S) and their maximum allowable active power flows.

Fig.1 IEEE RTS-24

A set of experiments was conducted to assess the adequacy of the mathematical expectation of power shortage.Table 1 shows the time consumed to generate and analyze 10 000 states with the number generators studied.

Table 1 Calculation time for 10 000 states using various PRNGs and QRNGs

As shown in Table 1,Mersenne Twister was demonstrated to be the fastest,and the Hammersley sequence algorithm was the slowest.The Sobol sequences were the fastest among the QRNGs.

The next step in the analysis of the presented number generators was to assess these for the speed of attainment of the specified stop criterion.In this case,the time of the calculated state analysis as well as the running time of the algorithm of the random number generator were considered.Table 2 shows the results of the analysis of PRNGs and QRNGs.

As shown in Table 2,the Sobol sequences indicate the best results.

Table 2 Number of iterations and calculation time required to achieve a stop criterion of 0.0065 for various PRNGs and QRNGs

3 Improved models of EPS power shortage minimization

An important component of the adequacy assessment methodology based on the Monte Carlo method is the correspondence of the power-shortage minimization model to the real-world conditions of EPS operation.The adequacy assessment only involves the analysis of EPSshortage conditions.It is considered that if such conditions are feasible in reality,the dispatching service and automatic control systems would be capable of rationally using all types of reserves available in the EPS.This would,in turn,minimize the power shortage.It is important for the power-shortage minimization model to reflect the physical limitations of the EPS with maximum accuracy.

Power-shortage minimization models evolved progressively as this problem was implemented.Furthermore,computational and mathematical technologies were developed.Several models have been developed.These differ in the extent to which these factor in various EPS functioning features that affect the correctness of determining the power shortage and other reliability indices,as well as the complexity and detail of the energy system representation.In the first stage of the development of the method to assess EPS adequacy,the power shortage minimization model was represented as a linear programming problem[21-23].These formulations did not consider power transmission losses.Such models have certain limitations that affect the accuracy of determination of power shortage.These models also have the problem of non-uniqueness in the power shortage distribution by the reliability zone.It can result in distortion of the real adequacy indices.These models can be used to estimate the EPS power shortage and can be applied only to the longterm (≥10 years) development of power systems,when the initial data forecast uncertainty is essential and calculation errors can be offset by forecast inaccuracy.

The next step of improvement was to consider power transmission losses in the interzone tie lines in the model for power shortage minimization[23-25].Originally,the power losses were set to depend linearly on the transmitted power.This resulted in an improvement in the accuracy of calculations of EPS power shortage,its distribution over reliability zones,and the accuracy of the determined EPS adequacy indices.

Further improvement of the accuracy of the powershortage minimization model involves the formulation of the problem given the quadratic relationship between the power loss and power transmitted via the interzone tie lines[23-26].The problem of power shortage minimization of the analyzed states of the EPS given the quadratic transmission losses in the power lines of the interzone tie lines can be written in the following form:

Determine

subject to the power balance constraints

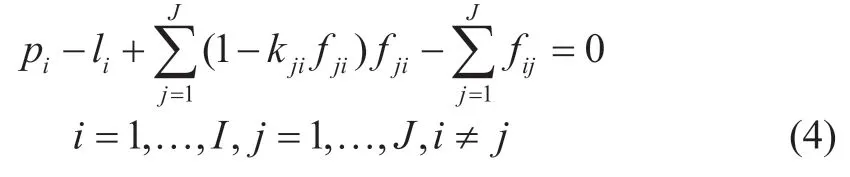
and the constraints on variables

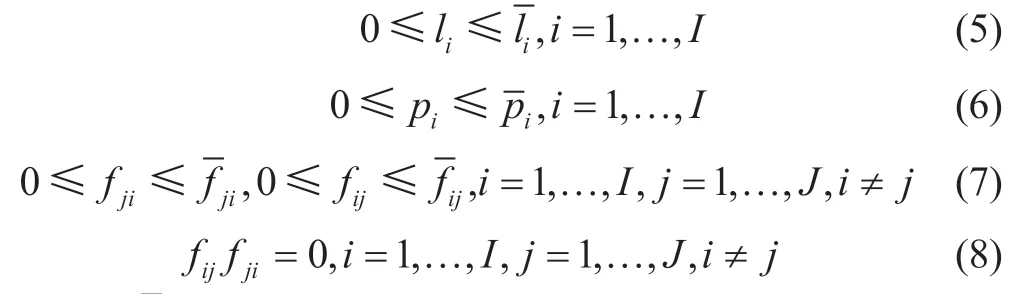
whereisthegiven(predicted)powerconsumptionin reliabilityzonei,MW;liis theactual(certain) power consumption in reliability zonei,MW;is the overall value of the operating power for generating plants in reliability zonei,MW;piis a certain (actual) load of generating units in reliability zonei,MW;is the transfer capability of the tie line between zonesjandi,MW;is the transfer capability of the tie line between zonesiandj,MW;fjiis the actual loading of the tie line between zonesjandi,MW;fijis the actual loading of the tie line between zonesiandj,MW;andkjiare coefficients of specific losses of power when transmitted from reliability zonejto reliability zonei.

A further development of the power shortage minimization model is the statement using a network coefficient matrix,or a first-order sensitivity matrix indicating the dependence of the variations in power flows through the interzone tie lines on the variations in the balance of power in EPS reliability zones[12,25-27].Network coefficient matrices are used to reflect the actual feasible EPS load flow,which depends on various factors such as the reactance of the line.

In this case,it is necessary to assess the minimum shortage of power of the EPS similarly as in the previous statement.However,the constraints of the following type must be considered,rather than the constraints of balance (4):

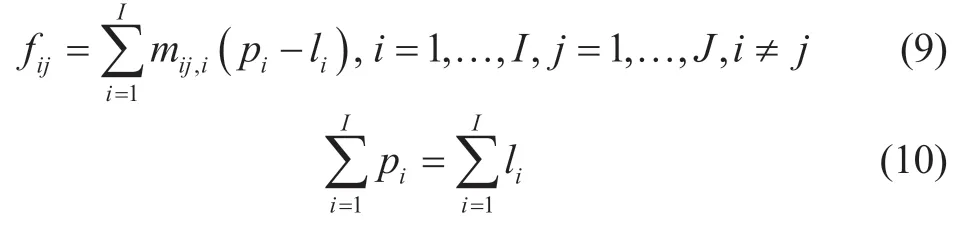
wheremij,iis the coefficient of the power distribution from thei-th reliability zone to the balancing reliability zone to the tie line between EPS reliability zonesiandj.It is determined by calculations of steady-state power flows.

Models (3) and (5-10) are linear.It does not consider active power losses.The development of this model considers both network coefficients and quadratic power losses.In this case,the balance constraints are of the following form:

The considered models of power shortage minimization were studied using IEEE-RTS-24 (Fig.1 (b)).

Tables 3,4,and 5 present the calculation data when the mathematical models under study were used.Moreover,the experiment was conducted for heavy load conditions with a load increase step of 10% to increase the maximum power consumption in all the reliability zones.

Table 3 Power shortage values in the study of the model with quadratic losses under heavy load conditions,MW

Table 4 Power shortage values in the study of the model with matrix of network coefficients (MNC) under heavy load conditions,MW

Table 5 Power shortage values in the study of the model with MNC+ quadratic losses under heavy load conditions,MW

According to the analysis of the initial state with the balance of power in the reliability zones,the reliability zones Z3 and Z4 are deficient.According to the analysis of the power shortage of the original EPS option for all the models under study,the transfer capability of the EPS network is sufficient to transmit power in the required amount from the reliability zones with surplus generation to the deficient zones.The results indicate the shortage of power for the analyzed models when the power consumption in the reliability zones increases by 10%.However,the power shortage occurs only in the reliability zone Z4 in the quadratic loss model,and in the reliability zones Z3 and Z4 in the remaining models.It is noteworthy that in the mathematical model wherein quadratic losses occur,the total quantity of power shortage is low (51.76 MW) compared with the other models analyzed (216.65 MW).This reveals the additional power transmission constraints that originate when we consider network coefficients.At the third load-increase step (30%),a significant difference remains between the power shortage in the model with quadratic losses and that in the other two models.In addition,there appears to be a marginal difference between the results of the models with MNC and MNC + quadratic losses (837.1 MW and 837.62 MW,respectively).This is because of increases in the power transmitted over the controlled cut sets and power transmission losses.

4 Use of machine learning methods in the analysis of calculated states of EPS

The minimization of the power shortage for the calculated states yields certain parameters that characterize EPS reliability.The determination of power shortage minimization is a difficult problem.This ultimately affects the performance of the entire adequacy assessment methodology and its applicability in solving subsequent problems such as the determination of the economically optimal reserves of generating capacity in the EPS.An alternative approach to solving this problem is the use of machine learning methods.These can increase the speed of the adequacy assessment.Machine learning methods are increasingly being used to solve various electric power problems.These methods are most widely used to predict various events and parameters.These are also used to solve analytical problems[28-30].In this study,it is proposed to use these for analyzing the calculated states in the problem of EPS adequacy assessment using the Monte Carlo method.This is the first time that such a solution has been proposed.

When we approach the problem being solved in the most comprehensive manner,the problem of power shortage minimization is best suited to the concept of multitask regression.This is because according to its conditions,it is necessary to identify a set of desired values such as system and nodal shortages,power flows with identical input data on the state of EPS,and loading of generating units according to operating conditions in zones.

The technique involves the division (into two subsets) of the total number of calculated-states generated to calculate the adequacy indices[31,32].The first subset has a smaller size than the second and constitutes a training subsample.Here,the desired values are determined using an algorithm based on optimization methods.The obtained training sample is employed to construct regression functions for multitask regression,whose purpose is to learn to recognize the necessary parameters of EPS reliability according to certain criteria.The optimized values for the second set of states are determined using a multitask regression model.The complete scheme for calculating adequacy using the Monte Carlo method with multitask regression is shown in Fig.2.

Fig.2 Algorithm for adequacy assessment using Monte Carlo method with multitask regression

Multitask regression aims to predict multiple independent continuous target variables simultaneously based on the same set of input variables.Such problems are normally solved using ordinary regression (support vector machine,linear regression,gradient boosting,and random forest).Its number corresponds to the number of unknown variables.

The study identifies the most effective machine learning methods for solving the stated problem.A set of experiments is conducted to assess the adequacy of the mathematical expectation of power shortage determined for 10 000 calculated states for the system shown in Fig.1.The runtimes are presented in Table 6.The machine learning methods investigated include linear regression,support vector machine,random forest,and gradient boosting.

As shown in Table 6,the use of multitask regression generally reduces the calculation time.This is notwithstanding the need to determine a set of EPS reliability parameters (power shortages in each reliability zone,loading of power transmission lines,loading of generating units,etc.).The fastest methods are simple linear regression and gradient boosting.

The next step in the analysis of the presented methods is to assess the speed of achievement of the specified criterion.In this case,the time of analysis of the calculated state as well as the time required to select a training sample and train the model are considered.Table 7 presents the results of this analysis.

Table 6 Runtime of machine learning algorithms when calculating RTS-24

Table 7 Number of iterations and calculation time required to attain the stop criterion of 0.0065

The table indicates an increase in the convergence rate with respect to the calculation of the EPS adequacy assessment using the Monte Carlo method without machine learning methods.Linear regression and gradient boosting retain their prominence in terms of complex rate,although random forest is the leader in terms of the convergence rate.

5 Conclusion

This study presents several directions for the development of a methodology for adequacy assessment of electric power systems using the Monte Carlo method.This is not an exhaustive set of directions for developing this methodology.The results presented in this study were obtained from the authors.The first strand uses efficient random-number generators to generate the calculated states of the electric power system.The observations of the research on pseudo-and quasi-random number generators indicated that the generator of quasi-random numbers of Sobol sequences is the most effective.The second is to increase the adequacy of the EPS power-shortage minimization model.A model that considers the network coefficients and quadratic power transmission losses has been developed.The third line of development is the application of machine learning methods in the analysis of the calculated states of the electric power system.Research has revealed that the use of multitask regression can increase the adequacy assessment speed and simultaneously maintain the required accuracy of results.

Acknowledgements

This work was conducted within the framework of the project under state assignment (No.FWEU-2021-0003) of the RF Basic Research Program for 2021-2030 and with financial support from the Russian Foundation for Basic Research within the framework of the scientific project No 20-08-00550.

Declaration of Competing Interest

We declare that we have no conflicts of interest.