基于SVM 的地下采煤区沉陷灾害发育敏感性分区研究
2022-11-04薛永安邹友峰张文志张明媚柳广春宋明伟
薛永安,邹友峰,张文志,张明媚,柳广春,宋明伟
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.太原理工大学 矿业工程学院,山西太原 030024;3.河南省采空区场地生态修复与建设技术工程研究中心,河南 焦作 454000;4.山西能源学院地质与测绘工程系,山西 晋中 030600;5.中国科学院地理科学与资源研究所 中国科学院陆地表层格局与模拟重点实验室,北京 100101)
地下矿产采出后,开采区周围岩土体的原始应力平衡状态被破坏,岩土体上出现位移与变形[1],这是一个十分复杂的过程,是采矿、地质等许多因素及多场耦合综合影响的结果,在地表上表现为塌陷坑与地裂缝[2],属于矿山地质灾害的范畴,具有渐进性特点,本文称为沉陷灾害。沉陷灾害是地下采煤扰动导致地表快速或缓慢沉降的一种地质灾害,在矿区分布广泛,既造成大量土地资源损毁,又严重破坏当地的地形地貌景观,还会严重影响周边植物生长[2],也是诱发斜坡地质灾害和影响区域生态地质环境的重要因素。因此,开展地下采煤区沉陷灾害发育敏感性分区研究对国土综合整治与生态修复、下伏老采空区重大工程项目设计与稳定性监测、地质灾害防治与预警等至关重要,同时对地下采煤区生态环境修复战略[3]具有助力作用。
灾害敏感性是指在特殊地形或某些因素作用下发生灾害的可能性[4],灾害敏感性评价则是针对某一地区现存或潜在灾害空间分布概率的定性或定量分析。目前,地质灾害敏感性评价工作已经取得众多研究成果[5],针对地表沉陷灾害敏感性评价,主要集中在开采地下水引起的地表沉降[6-8]和废弃矿区地表沉降的灾害敏感性评价研究[9-11],提出了众多评价模型并被应用和开展对比分析[12-14],为沉陷灾害发育敏感性分区研究提供了评价模型选择参考。敏感性评价模型一般可分为定性模型和定量模型,随着研究的不断深入,更多评价模型被引入该领域[15-16],为灾害风险评估与定量评价提供了良好的模型基础。目前,常用的评价模型主要包括:频率比(Frequency Ratio,FR)[17]、确定性系数(Certainty Factor,CF)[18]、支持向量机(Support Vector Machine,SVM)[19]、随机森林(Random Forest,RF)[7-8]和自适应神经模糊推理系统(Adaptive-Network-Based Fuzzy Inference System,ANFIS)[20]等。在模型应用中,确定地表沉陷影响因子是沉陷灾害发育敏感性分区评价的前提,如有研究者认为覆岩岩性、地表坡度、采空区范围、岩体力学性质、地下水等是诱发地表沉陷的主要影响因素[21-22],沉陷灾害敏感性评价则是在上述基础上所做的进一步研究工作[23]。评价因子的可靠性选择,评价模型的适用性对比,为开展地下采煤区沉陷灾害发育敏感性分区研究提供了丰富的理论与实践参考[21-23]。
山西省太原市西山地区地下采煤强度高,沉陷灾害及次生地质灾害分布广泛,给人民生活安全及经济发展带来较大影响。文献[24]开展了崩塌、滑坡、不稳定斜坡和地面塌陷4 种地质灾害与发育特征因子之间关联性的空间统计分析,为太原西山地区沉陷灾害发育敏感性评价提供了特征因子选择参考。文献[25]针对斜坡地质灾害敏感性评价中地势起伏度提取最佳尺度开展了研究,为太原西山地区地质灾害敏感性评价时地势起伏度因子可靠提取提供了依据。
针对地下采煤区沉陷灾害发育敏感性分区,笔者选择在小样本情况下应用广泛的SVM 模型为敏感性评价模型,分别以不同年度核查编录的沉陷灾害作为模型建立与预测能力验证数据,开展太原市西山前山区沉陷灾害发育敏感性分区研究,以期为地下采煤区沉陷灾害及次生地质灾害防治提供科学的方法与数据支持。
1 研究区与数据源
1.1 研究区概况
太原市西山前山区位于山西省太原市西部山区(图1),北西以尖草坪区、万柏林区和晋源区行政界线为边界,南东以山前坡脚线为界,总面积441.063 km2。区内采煤活动历史悠久,已近百年,煤矿开采主要为地下开采方式,既有国有大矿,包括西铭矿、杜儿坪矿、官地矿、白家庄矿和西峪煤矿,还有分布广泛且数量庞大的乡办、村办、联营小型煤矿,逐渐在空间上形成了大矿与小矿既有邻近、又有重叠的地下采煤区,地表沉陷情况极其复杂,沉陷灾害及次生地质灾害分布广泛,部分地裂缝发育于山顶基岩或山体出露岩层(图2)。
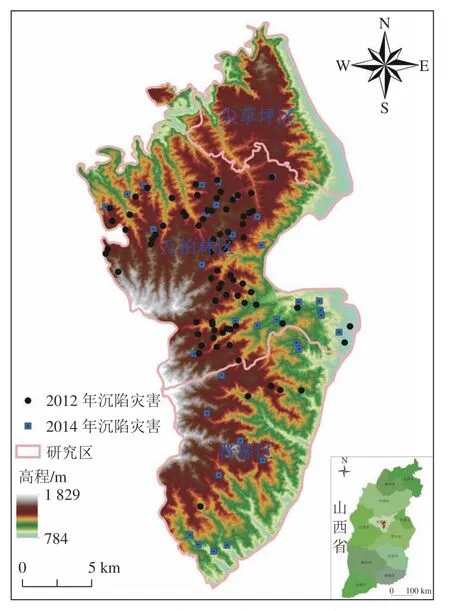
图1 太原市西山前山区地理位置Fig.1 Geographical map of Xishan area of Taiyuan City

图2 太原市西山前山区沉陷灾害Fig.2 Subsidence disaster in Xishan area of Taiyuan City
1.2 数据源
1) 沉陷灾害数据
收集到研究区2012 年、2014 年核查编录的地面塌陷与地裂缝灾害共113 处,提取地裂缝的中心位置,以点形式与地面塌陷构建沉陷灾害点图层,其空间分布如图1 所示。其中,2012 年79 处,2014 年34 处,数据来源于山西省太原市规划和自然资源局。
2) DEM 数据
在地理空间数据云网站下载了研究区的ASTER GDEM V2 数据,并重采样为30 m 分辨率的DEM 数据,作为研究区的数字地貌因子提取基础数据,高程中误差为±22.723 m[25]。
3) 地质数据
研究区1∶200 000 数字地质图来源于山西省太原市规划和自然资源局。
2 研究方法
沉陷灾害发育敏感性分区步骤如下:
(1) 收集研究区实际核查编录的2012 年和2014年的沉陷灾害空间分布数据,以2012 年发育的沉陷灾害为训练样本建立模型,以2014 年发育的沉陷灾害为验证样本评价模型预测精度。
(2) 从地形地貌和地质因素两个方面出发建立评价因子组合。
(3) 以评价因子提取结果输入基于机器学习思想的SVM 模型开展沉陷灾害发育敏感性评价,以受试者特征曲线(Receiver Operating Characteristic,ROC)下面积(Area Under the ROC Curve,AUC)作为定量评价指标对分区结果进行精度验证。
(4) 以自然间断点法进行等级划分并制作研究区沉陷灾害发育敏感性分区图。
总体技术路线如图3 所示。
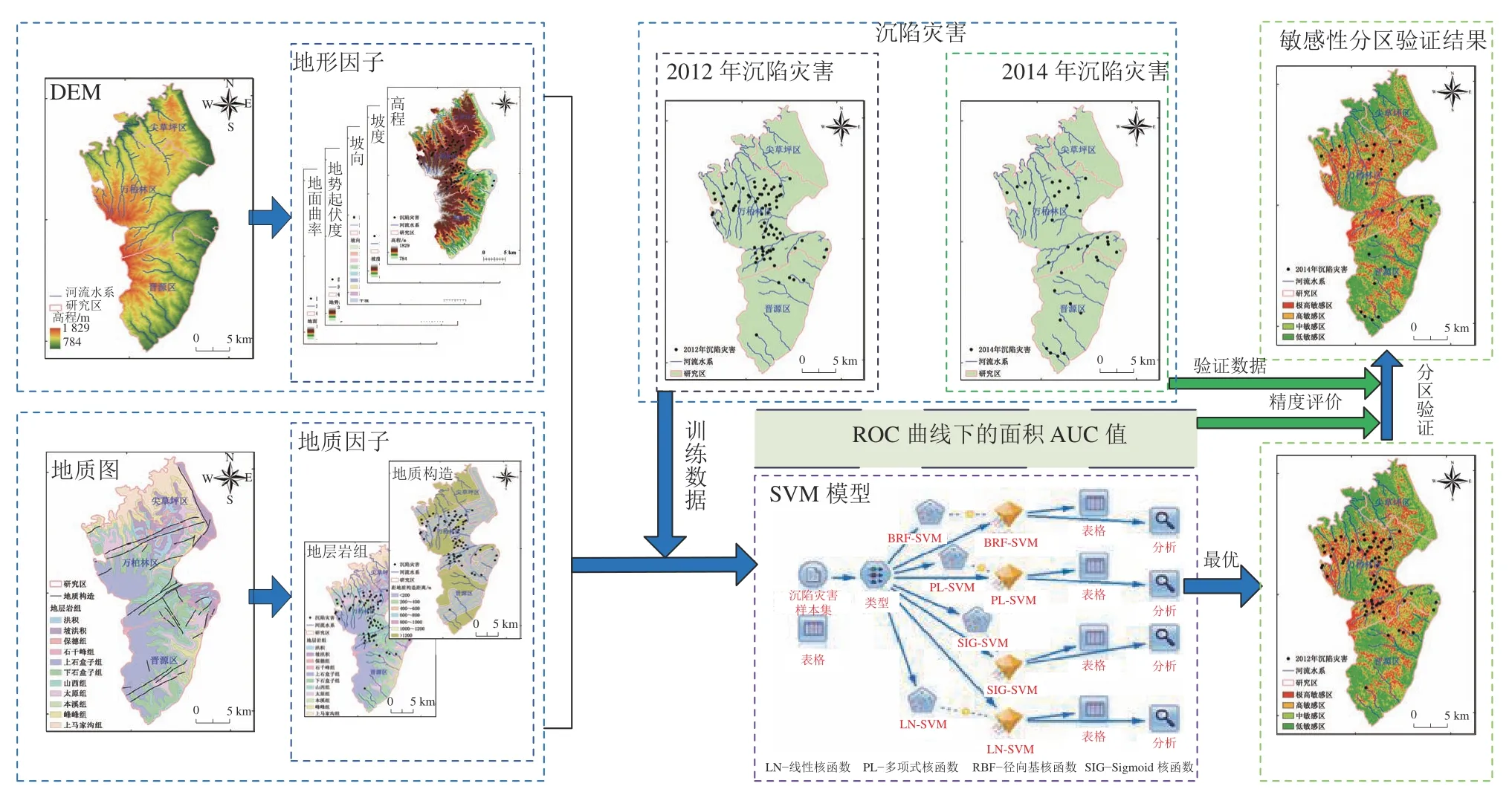
图3 总体技术路线Fig.3 Technology roadmap for the study
2.1 评价因子
针对地下采煤活动对矿区微地貌、土地利用等带来的扰动影响,文献[26-27]选择研究区中西部的杜儿坪煤矿南三盘区为对象,其中,文献[26]采用1∶10 000地形图所生产的3 期DEM 数据分别代表矿区采前、采中和采后3 个时期的地形表面,开展了数字地貌时空演变特征分析,结果表明坡度与地势起伏度统计结果随时间推进而变化明显,坡向也有一定的影响。因此,DEM 数据的获取时间对数字地貌因子分析结果是否可靠具有重要约束,灾害敏感性预测研究中应尽可能采用与沉陷灾害发育时间相匹配的DEM 数据进行数字地貌因子提取。文献[27]则以采前、采中和采后的5 期遥感影像为数据源,采用最小距离分类法进行了矿区土地利用信息提取与演变分析,结果表明,土地利用类型转移过程和方向与煤炭开采扰动过程相吻合。因此,遥感影像时相不同,所提取的土地利用信息则不同,以特定年份的遥感影像所提取的土地利用数据和植被覆盖数据与历史编录的沉陷灾害数据进行相关分析,其结果不确定性极大。
沉陷灾害影响因子众多,在开采沉陷预计中多采用地形地貌、地质因素、采煤方法、煤层厚度、埋深、工作面尺寸等因子[1,28],专家学者基于不同目的建立了不同的影响因子序列。受地下采煤相关数据获取困难、定量表述不足制约,并考虑方法的通用性,本文在现有研究的基础上[24-25],综合考虑地下采煤区数字地貌特征和土地利用时空演变的影响[26-27],从地形地貌与地质因素出发,选取高程、坡度、坡向、地势起伏度、地面曲率、地层岩组、地质构造共7 个因子作为沉陷灾害发育敏感性评价因子组合(表1)。
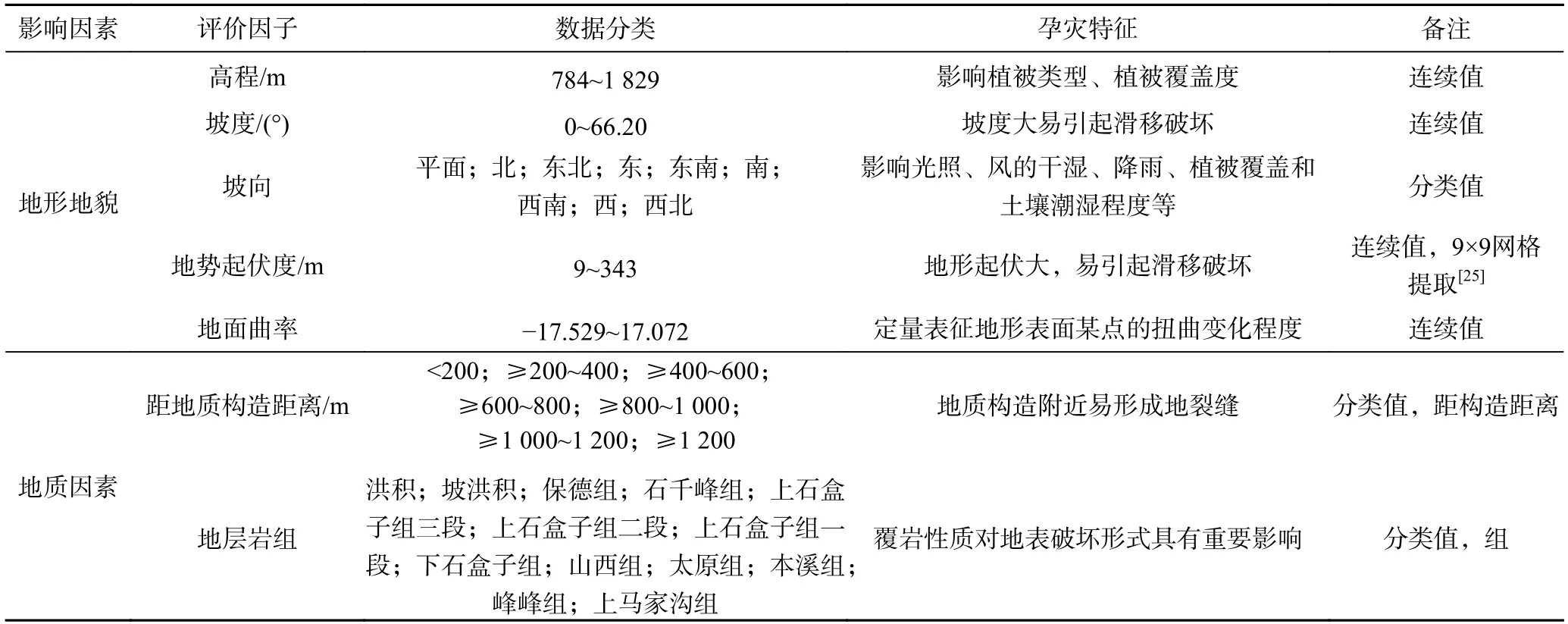
表1 研究区沉陷灾害敏感性评价因子Table 1 Assessment factors of subsidence disaster sensitivity in the study area
以ASTER GDEM V2 数据在ArcGIS 软件中提取高程、坡度、坡向、地势起伏度和地面曲率,基于1∶200 000 地质图提取地层岩组与地质构造信息,利用ArcGIS 软件制作研究区2012 年沉陷灾害发育敏感性评价因子图(图4)。
经图4 统计,沉陷灾害在各行政区之间的空间分布规模差异性较大,2012 年的平均发育密度为0.179 处/km2,万柏林区的发育密度最高,达到0.336 处/km2,高于研究区平均水平。其次是晋源区,为0.034 处/km2,发育密度相对较低。

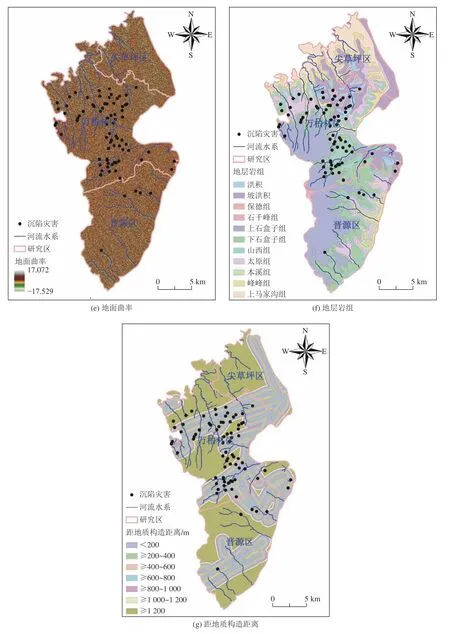
图4 太原市西山前山区沉陷灾害评价因子Fig.4 Assessment factors of the subsidence disaster in Xishan area of Taiyuan City
2.2 支持向量机(SVM)
支持向量机是一种基于最大间隔的线性判别分类方法,其功能强大,可以最大化模型的预测准确度,被认为是目前针对小样本统计估计和预测学习的最佳理论,最早被用于研究小样本情况下的机器学习[29],在地质灾害敏感性评价研究中应用较多[13,30]。
SVM 通过引入核函数有效地解决了非线性分类问题,使敏感性评价中的非线性分类计算复杂度不再取决于空间维数,而是取决于用于建模的沉陷灾害样本数量,尤其是其中支持向量的灾害点数量。显然,核函数是SVM 克服维数灾难实现沉陷灾害敏感性评价有效分类的关键。SVM 常用核函数(表2)主要有线性核函数(Linear Kernel,LN)、多项式核函数(Polynomial Kernel,PL)、径向基核函数(Radial Basis Function,RBF)和Sigmoid 核函数(Sigmoid Kernel,SIG)[13]。

表2 SVM常用核函数[31]Table 2 Common kernel functions of SVM[31]
目前,地质灾害敏感性评价中径向基核函数应用较多[30],但研究区内沉陷灾害样本数量较少,应对比4种核函数SVM 模型的预测精度,选择最优核函数建立SVM 预测模型。
沉陷灾害敏感性分区SVM 模型预测步骤如下:
(1) 建立研究区沉陷灾害数据集,包括训练样本集和验证样本集。
(2) 提取沉陷灾害点在评价因子图中的值,作为属性值记录下来,包括:高程、坡度、坡向、地势起伏度、地面曲率、地层岩组和距地质构造的距离。
(3) 建立4 种SVM 模型,包括LN-SVM 模型、PL -SVM 模型、RBF-SVM 模型和SIG-SVM 模型。
(4) 采用训练样本对4 种SVM 模型进行训练,统计评价因子在每一种模型中的权重排序,分析模型预测正确率与错误率,避免出现过拟合和欠拟合。
(5) 选择预测正确率最高的SVM 模型作为沉陷灾害敏感性分区预测模型。
(6) 采用验证样本评价最优SVM 模型的预测精度,对比训练样本的预测精度,分析预测结果的合理性。
2.3 精度评价
敏感性评价是一个二值分类问题,一般将样本分为正类和负类,现有研究中通常采用真正类率和真负类率构建受试者特征曲线(ROC),利用ROC 曲线下的面积(AUC 值)作为敏感性分区预测精度的度量[13,31],AUC 值的范围为[0,1],值越大越好,表明模型预测能力越强,灾害敏感性分区预测结果精度越高。
根据AUC 值的大小可以划分敏感性分区预测模型的精度等级(表3)[13]。

表3 敏感性预测模型精度等级[13]Table 3 Accuracy levels of sensitivity prediction model[13]
对于二值分类问题,假设C1为正类,C2为负类,对应的2×2 混淆矩阵见表4。其中,TP 表示分类方法准确预测为C1的点的数目;FP 表示分类方法预测为C1,但实际属于C2的点的数目;FN 表示分类方法预测为C2,但实际属于C1的点的数目;TN 表示分类方法准确预测为C2的点的数目。

表4 二值分类混淆矩阵Table 4 Confusion matrix of binary classification
敏感性Sp,也称为真正类率,是C1中所有点被正确预测的比例,计算公式[32]如下:

特异性(Xp),也称为真负类率,计算公式[33]如下:

AUC 值计算公式[33]如下:
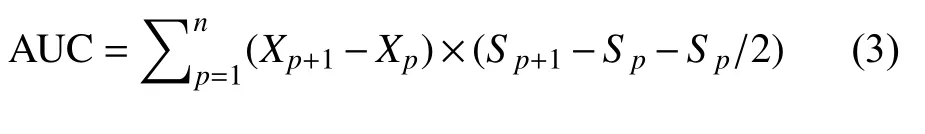
3 沉陷灾害发育敏感性分区结果与讨论
3.1 结果
本文按照图3 的技术流程开展研究区沉陷灾害发育敏感性分区预测。
训练样本和验证样本分别随机生成同等数量的非沉陷灾害样本,建立由79(沉陷灾害)+79(非沉陷灾害)个样本点组成的训练样本数据集,共有训练样本点158 个。建立由34(沉陷灾害)+34(非沉陷灾害)个样本点组成的验证样本数据集,共有验证样本点68 个。其中,沉陷灾害样本点与非沉陷灾害样本点之间的距离为500 m。
3.1.1 评价因子权重
利用SPSS 软件统计4 种常用核函数SVM 模型评价因子的重要性排序,结果对比如图5 所示。
图5 显示,4 种模型中评价因子的权重顺序并不相同,其权重从高到低的排列顺序分别为:
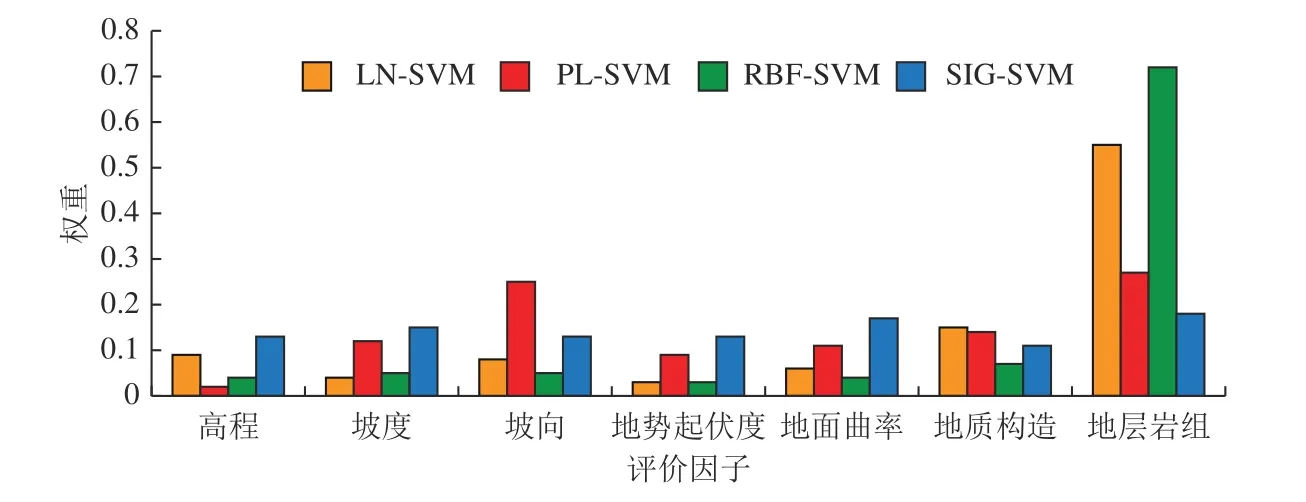
图5 研究区不同核函数SVM 模型沉陷灾害敏感性评价因子权重对比Fig.5 Comparison of the weight of subsidence disaster sensitivity evaluation factors in different kernel function SVM models in the study area
(1) LN-SVM 模型:地层岩组,地质构造,高程,坡向,地面曲率,坡度,地势起伏度。
(2) PL-SVM 模型:地层岩组,坡向,地质构造,坡度,地面曲率,地势起伏度,高程。
(3) RBF-SVM 模型:地层岩组,地质构造,坡向,坡度,地面曲率,高程,地势起伏度。
(4) SIG-SVM 模型:地层岩组,地面曲率,坡度,地势起伏度,坡向,高程,地质构造。
3.1.2 SVM 模型优选
4 种核函数SVM 模型预测正确率在SPSS 软件中的统计结果见表5。
由表5 可以看出,4 种核函数SVM 模型的预测正确率由高到低排列为:PL-SVM 模型、LN-SVM 模型、RBF-SVM 模型、SIG-SVM 模型,其中,PL-SVM 模型表现最优。
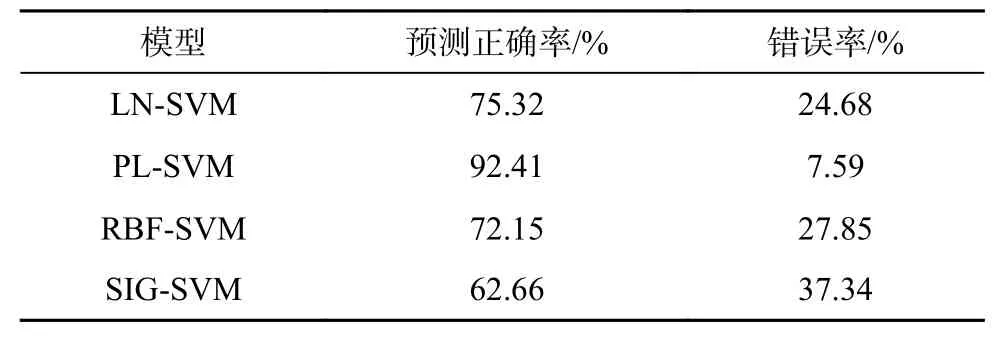
表5 研究区不同核函数SVM 模型预测正确率Table 5 Prediction accuracy of SVM models with different kernel functions in the study area
3.1.3 评价结果
通过因子权重分析及预测正确率对比,PL-SVM模型的因子重要性排序更合理,预测正确率最高,明显优于其他3 种模型。因此,本文采用PL-SVM 模型进行研究区沉陷灾害发育敏感性分区预测,并在ArcGIS 中采用自然间断点法将研究区划分为4 个敏感性等级,分别为:极高敏感区、高敏感区、中等敏感区和低敏感区,得到研究区沉陷灾害敏感性分区结果(图6a),验证结果如图6b 所示,对训练样本和验证样本的分区统计结果见表6。
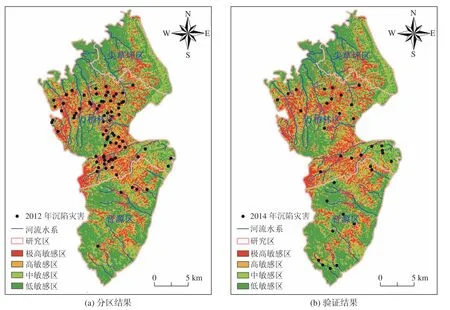
图6 研究区沉陷灾害敏感性分区与验证Fig.6 Sensitivity zoning and verification of subsidence disaster in the study area

表6 研究区沉陷灾害敏感性分区统计Table 6 Statistics on sensitivity zoning of subsidence disaster in the study area
由表6 可以看出,PL-SVM 模型通过训练样本和验证样本分别统计得到的频率比值(频率比=灾害点比例/分区栅格比例)均随敏感性等级升高而递增,经对比其趋势均符合线性函数,拟合方程分别为:
(1) 训练样本频率比趋势:y=-0.791x+3.24,R²=0.999 7。
(2) 验证样本频率比趋势:y=-0.514x+2.47,R²=0.988 7。
其中,y为频率比值;x为敏感性等级,极高为1,高为2,中为3,低为4。
可以看出,2 个拟合方程的决定系数R²的值均接近于1,表明PL-SVM 模型通过训练样本和验证样本所计算的频率比值与敏感性等级之间呈良好的正相关,均以更小的极高与高敏感性分区面积分布了更多的沉陷灾害。训练样本频率比的趋势较验证样本频率比的趋势相关性更好,表明2012 年与2014 年发育的沉陷灾害在研究区内的空间分布略有不同。
3.1.4 精度评价
利用式(3) 分别计算训练样本与验证样本在PLSVM 模型敏感性分区预测结果中的AUC 值,其中,以2014 年沉陷灾害作为验证样本的PL-SVM 预测模型的AUC 值为0.755,低于以2012 年沉陷灾害作为训练样本的PL-SVM 预测模型的AUC 值(0.854),表明PL-SVM 模型在验证样本集的预测精度略低于训练样本集,符合预测模型在测试数据集上的精度一般低于训练数据集精度的规律。但2 种模型预测精度均较高,训练模型精度等级为非常好,预测模型精度等级为好。预测精度表明,模型在训练样本与验证样本上既没有过拟合,也没有欠拟合,结果较为合理。
3.2 讨论
3.2.1 评价因子权重
由图5 可以看出,地层岩组在4 种模型中均是最重要的评价因子,表明沉陷灾害发育与地层岩组分布关系密切,是地面塌陷与地裂缝发育的最重要影响因素。尽管在SIG-SVM 模型中地质构造表现为影响最弱的因子,但从4 种模型中前3 位因子出现的频率可以看出,地质构造对沉陷灾害发育的影响仅次于地层岩组,表明在构造断裂附近,岩层破碎,地下采煤扰动再次打破断裂附近的岩体力学平衡,诱发地表塌陷或开裂。
由图5 可知,地势起伏度因子在LN-SVM 和RBFSVM 模型中均是沉陷灾害发育影响最弱的因子,在PL-SVM 模型中为次最弱因子,表明区域范围内高程最大值与最小值之间的差值大小对沉陷灾害发育影响较小。一般情况下,当沉陷灾害处于沟谷边缘时极易诱发崩塌与滑坡灾害,而沉陷灾害仅包括地面塌陷与地裂缝,因此,地势起伏度因子在敏感性评价中贡献较小。
由图5 同时可以看出,LN-SVM 和RBF-SVM 模型中地层岩组的权重远超其他因子,SIG -SVM 模型中各因子的权重相对平衡,地层岩组略高于其他因子,而PL-SVM 模型中地层岩组与坡向因子的权重明显高于其他因子,在评价因子组合分析中,既没有过分依赖某一个因子,也没有分散因子权重,其合理性高于其他3 种核函数模型。
3.2.2 预测模型优选
SVM 预测模型的性能优劣主要取决于核函数的选择,本文分别对比了LN-SVM 模型、PL-SVM 模型、RBF-SVM 模型和SIG-SVM 模型在研究区沉陷灾害敏感性分区中的预测精度,预测正确率分别为75.32%、92.41%、72.15%、62.66%,其中,PL-SVM 模型预测正确率明显高于其他3 种核函数SVM 模型,分别比LNSVM 模型、RBF-SVM 模型和SIG-SVM 模型的预测正确率高22.69%、28.08%和47.48%。SIG-SVM 模型的预测正确率是4 种模型中最低的,分别比LN-SVM模型、PL-SVM 模型和RBF -SVM 模型的预测正确率低16.81%、32.19%和13.15%。
由图5 可知,PL-SVM 模型的评价因子权重排序合理性最好,而SIG-SVM 模型则最差,与预测正确率完全一致,选择PL-SVM 模型作为研究区沉陷灾害发育敏感性分区预测模型是可靠的。
3.2.3 沉陷灾害敏感性分区预测结果
敏感性评价研究中通常采用总样本的70%或80%作为训练点建立预测模型,剩余30% 或20%作为验证点验证预测模型精度[30-31]。本文以研究区2012 年和2014 年实际发育的沉陷灾害分别作为训练样本和验证样本,基于PL-SVM 模型进行沉陷灾害发育敏感性分区预测。结果表明,2012 年沉陷灾害发育在极高、高、中、低4 个等级的数量百分比分别为49.37%、29.11%、17.72%、3.80%,极高和高敏感区分布了共78.48%的沉陷灾害。2014 年沉陷灾害发育在极高、高、中、低4 个等级的数量百分比分别为38.24%、26.47%、20.59%、14.71%,极高和高敏感区分布了共64.71%的沉陷灾害。
由图6 可知,2012 年沉陷灾害在研究区内有明显的聚集特征,2014 年则演变为随机分布,部分沉陷灾害出现在低敏感区,导致敏感性分区预测结果对验证样本(AUC=0.755)的精度略低于训练样本(AUC=0.854),但图6b 可以看出,模型的预测结果良好,2014 年新发育的沉陷灾害大部分位于极高和高敏感区,为沉陷灾害核查提供了重点区预测,可极大减少野外调查的盲目性与野外工作量。
3.2.4 综合分析
目前,地下采煤区地质灾害敏感性评价研究中一般将多年灾害点混合作为样本进行模型训练,但忽视了受采煤扰动影响的矿区地貌特征和土地利用时空演变[26-27],采用特定年份的灾害数据进行建模又需要面对样本数量过少对敏感性评价结果所带来的不确定性影响。今后应就此问题继续展开研究,利用遥感解译手段增加特定年份灾害样本数量,提升区域灾害点小样本情况下沉陷灾害发育敏感性分区预测精度。
研究区含煤地层出露,极高和高敏感区主要分布于王封煤业、西铭煤矿、杜儿坪煤矿、西峪煤矿、白家庄煤矿等多个大型煤矿区域,相比较地形地貌与地质因素,大、小矿地下采煤扰动是研究区沉陷灾害发育的主控因素。本文基于方法适用性考虑,未将地下采矿扰动影响列为敏感性评价指标,今后应继续研究如何定量化引入地下采矿相关指标参与沉陷灾害敏感性评价。
太原市西山地区近年所开展的采煤沉陷区治理效果明显,玉泉山城郊森林公园、长风城郊森林公园、四达沟生态恢复景区等分布于研究区东缘,生态地质环境恢复较好,但沉陷灾害极高和高敏感区与植被覆盖区重叠度较高,对区内地下水资源保护形成潜在威胁,应防止水资源破坏导致植被衰退而引起矿区生态环境再次恶化[28],也是矿山生态环境治理需要重点关注的区域。同时,分布于林地内的沉陷灾害点给遥感解译和野外调查带来困难,灾害数据集完备性受限,给敏感性分区评价结果的精准性与可靠性带来一定的影响。
4 结论
a.PL-SVM 模型是研究区沉陷灾害敏感性分区预测的最优模型,分别以2012 年和2014 年实际发育沉陷灾害点为训练模型和验证模型,其训练精度与验证精度均较高,且训练精度较验证精度高,对地下采煤区沉陷灾害发育敏感性分区具有良好的适用性和预测性。
b.PL-SVM 模型划分了研究区沉陷灾害极高、高、中和低敏感区4 个等级的面积比例,极高与高敏感区主要分布于万柏林区和晋源区边山一带,与研究区内大矿与小矿的重合带高度吻合。灾害点比例随敏感性等级升高而递增,与敏感性等级之间呈现良好的线性正相关。分区结果合理,对研究区沉陷灾害普查与防治重点区确定具有指导价值,对开展同类研究具有参考意义。
c.应进一步改进、完善评价因子组合,并选择更多评价模型开展对比,组建更可靠的沉陷灾害发育敏感性预测体系,同时收集研究区最新的沉陷灾害数据进行模型验证,为地下采煤区沉陷灾害发育敏感性分区预测提供最适用的结果。
