基于神经网络的轨道电路行车信号判断＊

贾智奥，禹建丽，刘泽源，陈洪根

（1.郑州航空工业管理学院管理工程学院，河南郑州 450046；2.河南科技大学材料科学与工程学院，河南洛阳 471000）

1 研究背景

随着“交通强国，铁路先行”的国家战略政策的实施，高铁已经成为人们出行必不可少的交通工具，铁路业也得到了突飞猛进的发展。近年来，随着铁路总里程数的增加，列车运行频次不断提高，铁路运行的安全性逐渐成为铁路运输的主题。在保证安全性的前提下，现代铁路还要提高铁路运输的效率，这就需要加大铁路设备的建设从而达到效率和安全的双重保障。而在各种铁路设备中，轨道电路系统是列车控制系统的核心，是信号系统的重要组成部分。轨道电路设备故障引起铁路信号系统故障的情况是铁路事故的重要原因之一[1]。因此，轨道电路行车信号判断的研究具有重要意义。

关于轨道电路方面的研究，国内学者已经取得了很多研究成果，曹雲梦等[2]采用BP 神经网络对高压脉冲轨道电路进行故障预测，实现了有关故障的识别分类，较传统预测方法更为可行高效；彭丽宇等[3]采用神经网络方法对铁路轨道不平顺进行预测分析，为铁路轨道养护维修提供技术支持；陶汉卿等[4]将多分支BP神经网络用于轨道电路故障预测，提高了预测准确率和计算效率；徐绍俊[5]以25 Hz 相敏轨道电路为研究对象，提出一种BP 神经网络与模拟退火相结合的故障诊断方法，有效提高了诊断效率和准确度；米根锁等[6]采用BP 神经网络对轨道电路的分路不良进行故障预警，得到可靠预警结果等。而ZPW-2000R 型无绝缘移频轨道电路是铁路区间段的基础设备，它根据主接入电压、调接入电压等数据来判断是否有列车占用车道[7]，来达到自动控制目的，以提高运输效率。

鉴于目前关于轨道电路行车信号判断的研究相对较少，本文提出一种基于神经网络的智能方法。通过采集轨道电路设备的列车运行实时数据，以轨道电路室内设备的主接收器调接入电压为输入，列车行车信号为输出，构建人工神经网络来判断轨道电路行车信号，通过调节各层神经元的权值达到机器学习的效果。测试实验研究表明，本文所提方法对轨道电路行车信号判断准确率达到100%，体现了人工智能方法的高效性和可行性。

2 神经网络模型

2.1 神经网络拓扑结构及学习算法

由于受到生物神经元结构的信息传递的启发[8]，W.McCulloch 和W.Pitts 提出了第一个神经网络模型，开启了人工神经网络发展的时代。人工神经网络具有自适应性、自学习性、自组织性、容错性，并且具有并行式处理能力、分布式存储能力、自动提取信息能力等[9]，其最主要的功能是非线性映射功能和较强泛化能力[10]。

BP 神经网络（Back Propagation Neural Network）是人工神经网络算法之一，是一种有效的分类和识别工具。BP 神经网络学习过程分为信息正向传播和误差反向传播过程。通过不断调整各层神经元的权值使实际输出与期望输出之间的误差不断减小[11]，直到满足精度要求。本文研究的BP 神经网络模型如图1 所示。

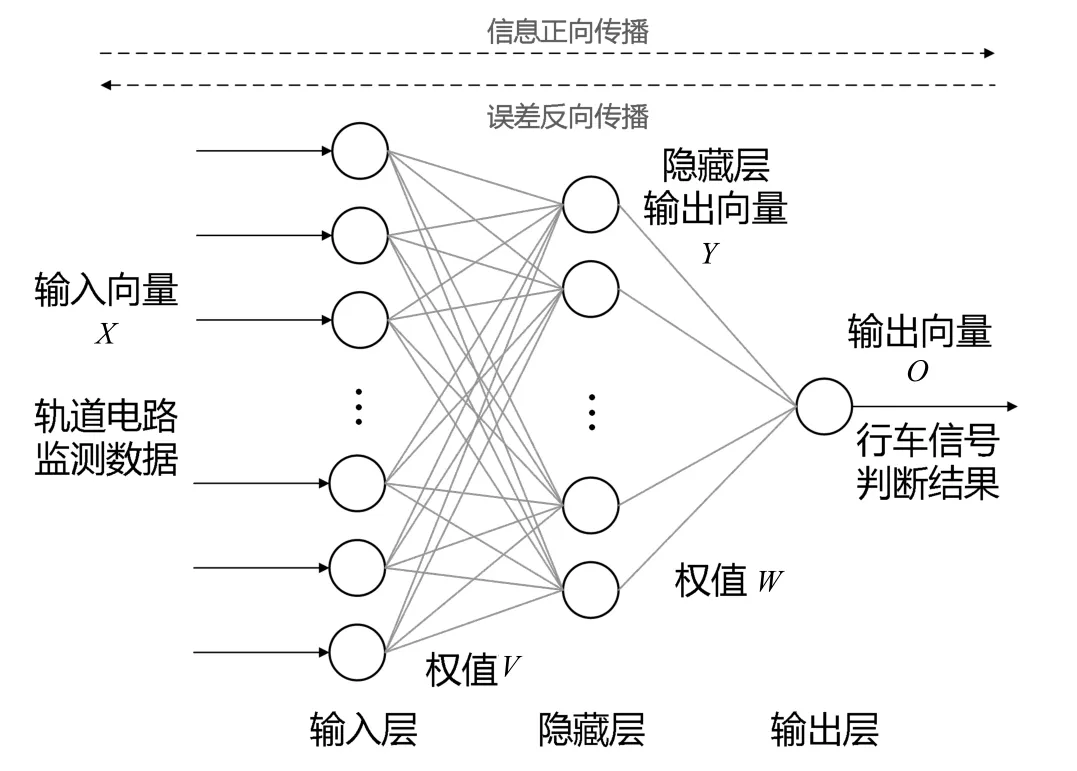
图1 神经网络结构

其中，网络的输入向量为X=（x1，x2，…，xi，…，xn）T，隐藏层输出向量为Y=（y1，y2，…，yj，…，ym）T，输出层输出向量为O=（o1，o2，…，ok，…，xl）T，期望输出向量为d=（d1，d2，…，dk，…，dl）T，输入层到隐藏层的权值矩阵：V=（v1，v2，…，vj，…，vm），隐藏层到输出层的权值矩阵：W=（w1，w2，…，wk，…，wl）。

对于输出层，有：

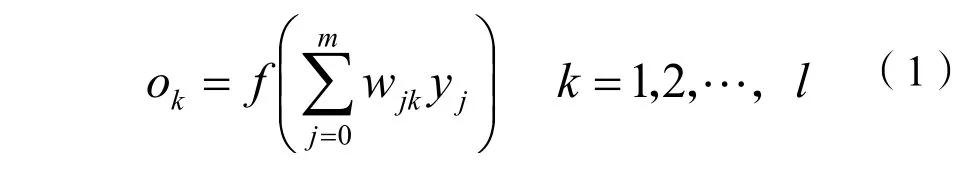
对于隐藏层，有：

公式（3）即期望输出与输出向量的误差，又称性能指标函数。

至此为网络的信息正向传播过程。若误差E不满足期望精度，则通过梯度下降法调整各层权值矩阵V和W，通过对误差E求偏导数，可得到输出层到隐藏层和隐藏层到输出层的权值调整分别为：

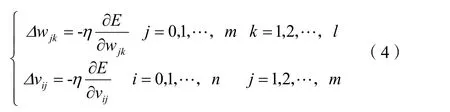
式（4）中，负号表示梯度下降；常数η∈（0，1），表示学习速率。

一般BP 神经网络需要经过多次的信息正向传播和误差反向传播不断减小误差[12]，可通过设置目标误差精度和最大迭代次数来使网络学习过程停止，最后通过保存相应的权值阈值即得到最终的模型。

尽管BP 神经网络的非线性映射能力和泛化能力很强，可有效解决很多实际问题，但采用负梯度下降调整权值可能会陷入局部最小值，故引入动量因子来修正权值，使网络学习速率加快且保持稳定。加入动量因子的权值调整为：

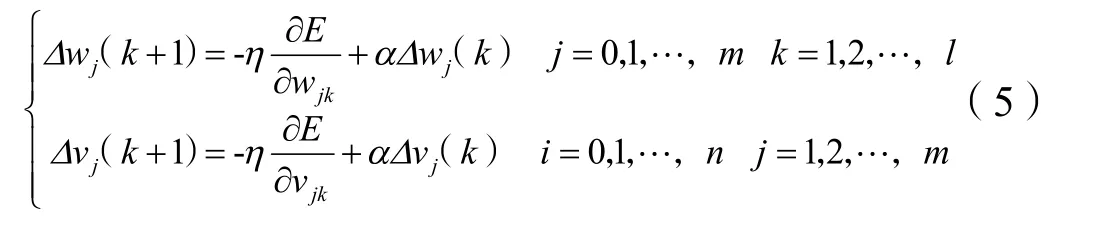
2.2 BP 神经网络模型构建

本文实验根据ZPW-2000R 型无绝缘移频轨道电路系统设备采集的实时电压数据来判断行车信号，且主接收器的调接入电压大小在轨道过车占用和正常空闲状态有较为明显的差别。实验采集的轨道过车占用和正常空闲的调接入电压数据变化如图2 和图3所示。

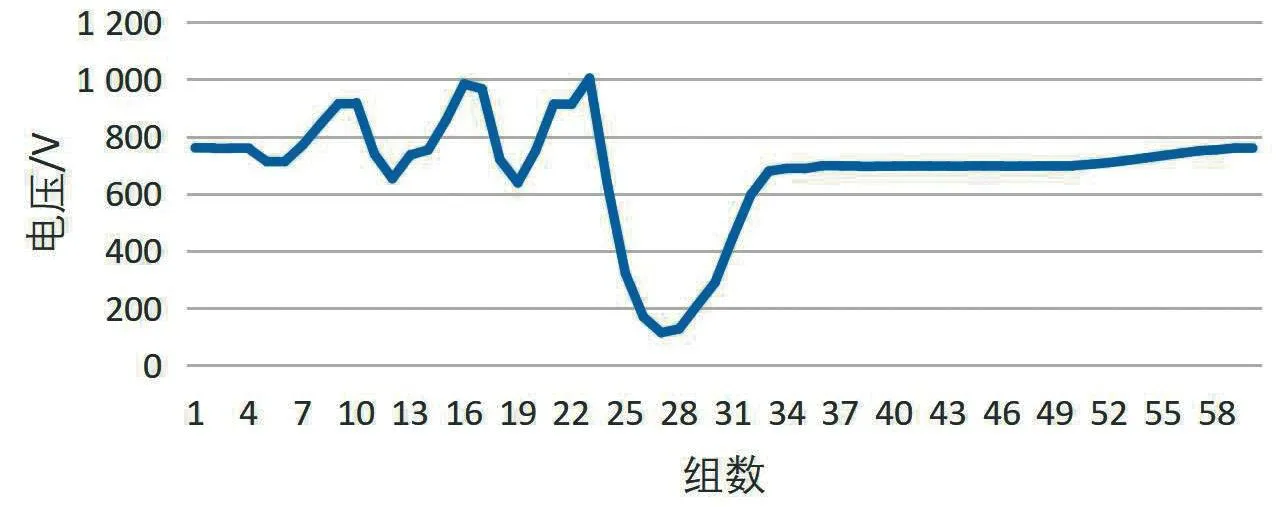
图2 轨道行车占用电压变化

图3 轨道正常空闲电压变化

神经网络模型构建的基础是网络的输入和输出，本文将轨道电路系统主接收器的调接入电压实时数据作为网络的输入向量，由于监测目的是判断是否有列车占用车道，所以将轨道电路行车信号判断结果（过车占用或正常空闲）作为神经网络输出。

通过采集得到了15 组轨道过车的实时电压数据，每组均为一个列向量，由于行车道每次过车的时间长短不一，导致了每组数据的维度不尽相同，所以取其中维度最高的60 维作为标准，将其余的数据前后补上车道正常电压数据至所有数据均达到相同的维数60，得到了最终的60×15 车道过车占用数据组成的矩阵，对于车道的正常空闲数据采集了36 组，把15 组车道过车数据其中的11 组和36 组正常数据其中的20 组合并为一个60×31 的矩阵，即为最终的神经网络训练输入矩阵P；其余的4 组过车数据和16 组正常数据合并为了60×20 的网络行车信号判断实验的测试矩阵P2；对于网络输出，定义“车道过车占用”为1、“车道正常空闲”为0，得到MATLAB 中神经网络训练输出矩阵T=[ones（1，11） zeros（1，20）]，同理可得网络行车判断实验的输出矩阵T2=[ones（1，4）zeros（1，16）]。

以下是神经网络模型的一些基本参数的确定和选取。

输入层和输出层神经元个数：由于神经网络输入矩阵P、输出矩阵T的维度分别为60 和1，确定输入层和输出层神经元个数分别为60 和1。

激活函数：本文网络模型选取transig 函数为隐藏层激活函数，purelin 线性传递函数为输出层激活函数，训练函数为traingdx。运用信号正向传播、误差反向传播的方式不断调整各层之间的权值，减小误差，提高准确率。

损失函数：模型的损失函数表征出了所有样本与实际值的误差总和。本文的回检实验采用默认的均方误差（MSE）为性能函数，而行车判断实验采用平均绝对误差（MAD）和均方误差（MSE）来作为性能函数，其计算公式为：

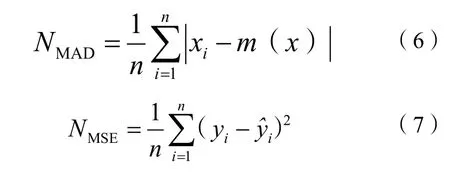
3 神经网络训练

采用MATLAB R2018b 软件，先将输入矩阵P进行归一化处理，建立神经网络模型，并进行回检，得到初始回检结果如图4 所示。

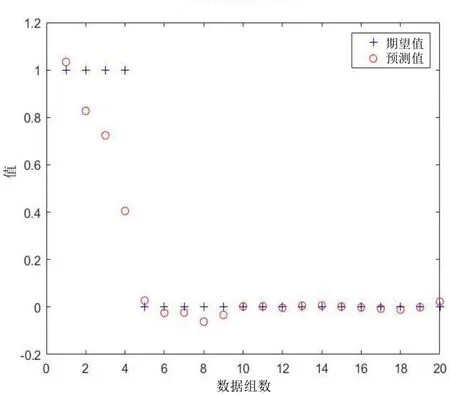
图4 初步回检结果

从图4 可以看出，后3 组车道过车数据和前5 组车道正常数据的判断结果较差，因此，后续实验将所有对应数据打乱顺序，之后再输入到神经网络中进行算法学习。

而隐藏层神经元个数依据经验公式：

式（8）中：p、m和n分别为隐藏层、输入层和输出层神经元个数；α为1～10 的常数。

由上述公式（8）可以得出隐藏层神经元个数应介于9～18。

该行为中国工商银行安徽省分行，在安徽省内，其综合实力排名靠前，所以此结果证明了该模糊综合评判模型的有效性和可行性。

通过神经网络算法训练、回检及行车判断实验，发现当隐藏层神经元个数不同时模型回检的均方差均在10-5量级，差别较小，所以采用行车判断结果的平均绝对误差和均方差来确定隐藏层神经元个数。并由公式（6）（7）计算出隐藏层神经元个数为9、10、11、12、13、14、15、16、17、18 的平均绝对误差分别为0.369 00、0.366 76、0.293 63、0.315 26、0.401 32、0.375 35、0.388 71、0.418 65、0.357 28、0.382 78，均方误差分别为0.298 91、0.293 73、0.195 44、0.221 63、0.342 88、0.320 35、0.335 56、0.366 99、0.307 85、0.339 02。

行车判断结果误差与隐藏层神经元个数的关系如图5 所示。由图可知，2 种误差变化较为稳定，p为11 时均达到最小值为0.293 63 和0.195 44。

图5 隐藏层神经元个数与误差关系

当p=11 时，网络训练的均方差随迭代次数的变化如图6 所示，由图可知，算法进行到第400 代时，均方差逐渐趋于稳定，当进行到1 000 代时，算法停止，即达到最大迭代次数的停止条件，且网络均方差在第986 代达到1.27×10-5。

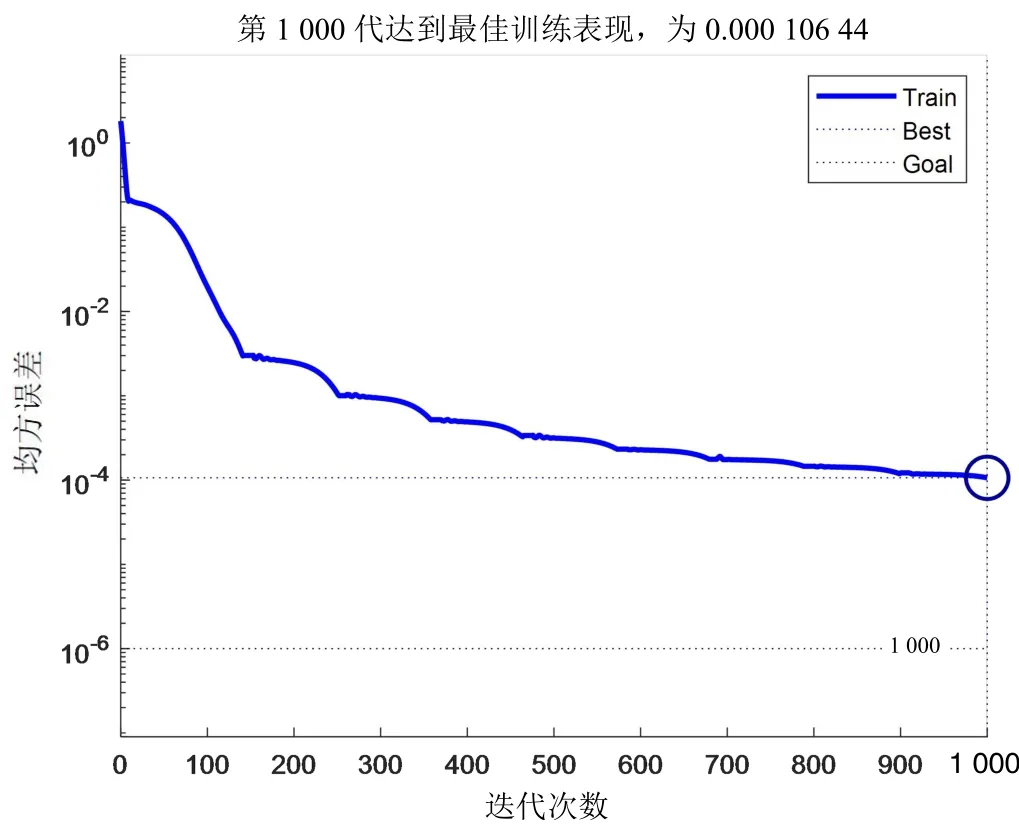
图6 网络均方差变化图

此外，算法的迭代次数、学习率、目标精度等参数也会对判断结果产生一定的影响。

对于学习率的选取，太低的学习率会减缓网络的训练速度，过高的学习率又会对损失函数产生影响，分别对学习率为0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10 进行实验，通过比较行车判断结果的误差来确定学习率，结果如图7 所示。

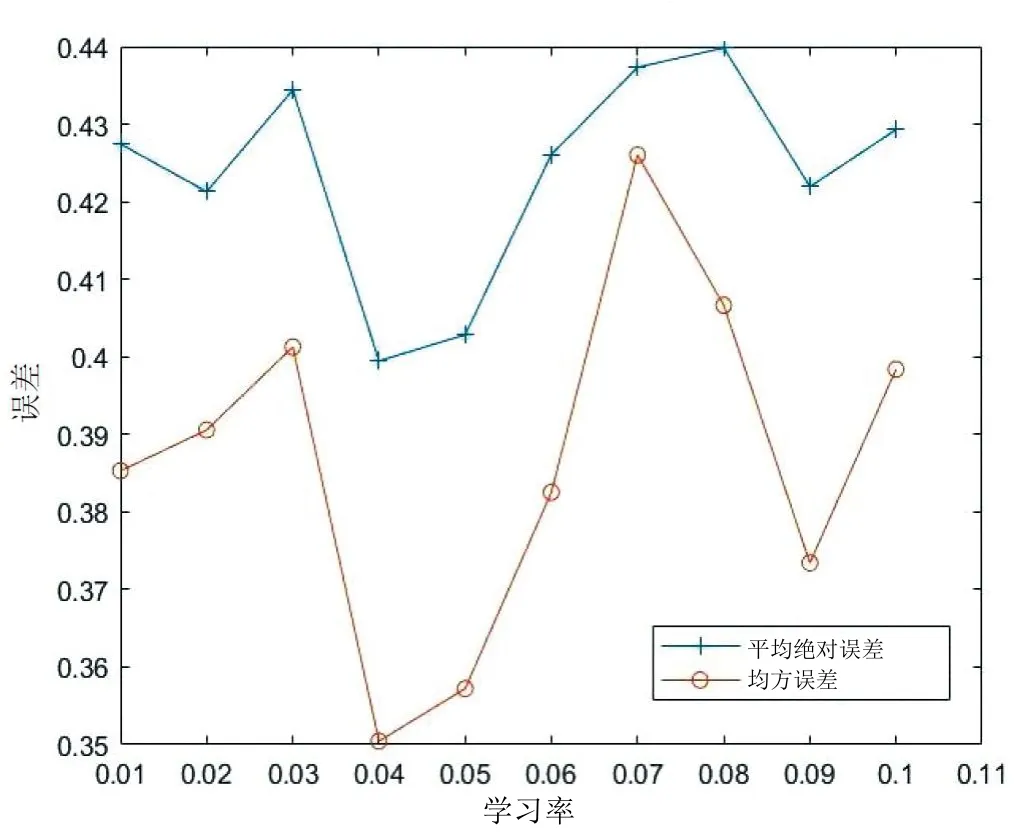
图7 学习率与误差关系

从图7 可以看出，当学习率为0.04 时，两种判断误差均达到最小，所以算法的学习率设置为0.04。

在反向传播过程中动量因子的引入，既可加快学习速度又可保持算法稳定，具体表达式为：

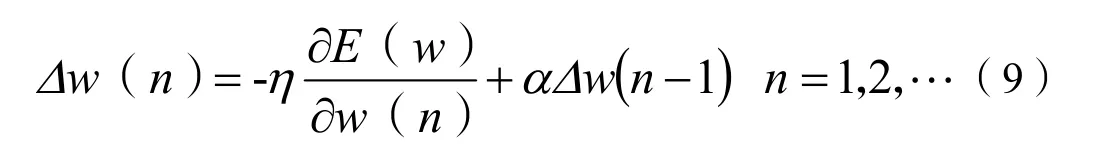
公式（9）中第二项为动量项，α∈（0，1），为动量因子。分别对0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9 进行训练，得到动量因子和判断结果误差的关系如图8 所示，从图中可以看出，动量因子为0.1 时两种误差均达到最小，所以算法的动量因子设置为0.1。

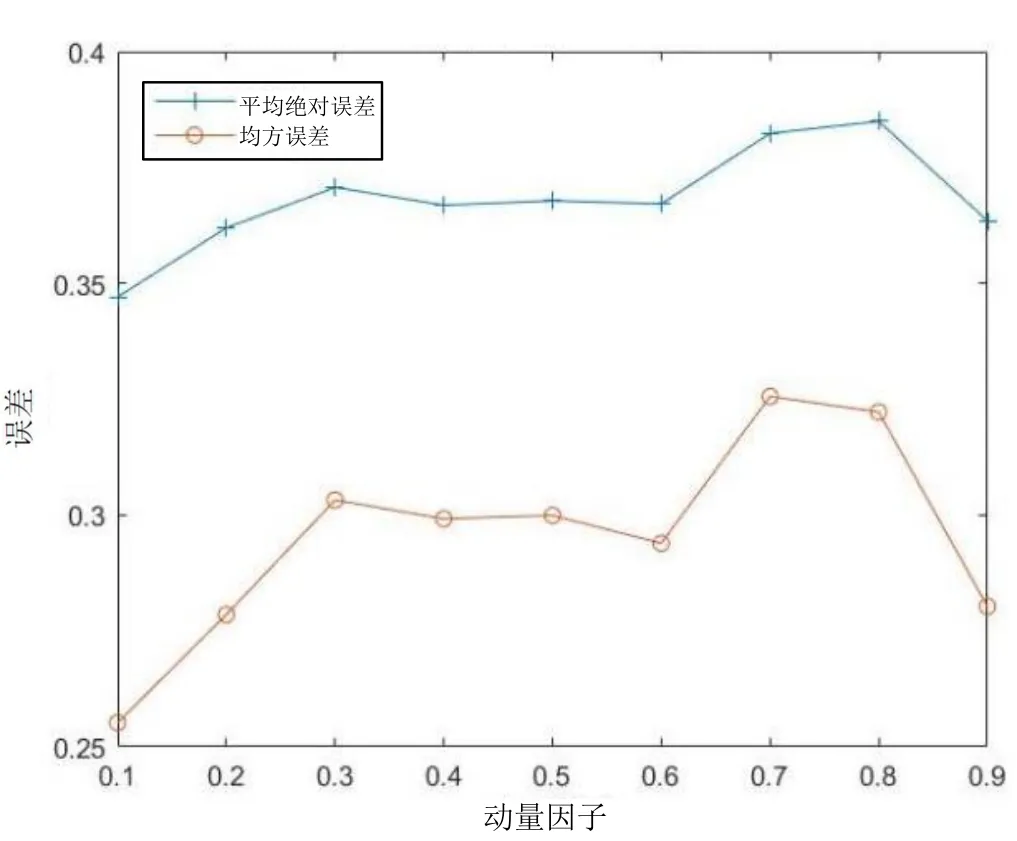
图8 动量因子与误差关系

本文确定的算法的相关参数如表1 所示。

表1 神经网络模型参数

4 BP 神经网络回检实验及行车判断

采用p=11 的神经网络判断模型进行回检实验，将31 组行车信号实时数据（其中包括11 组过车占用数据和20 组正常空闲数据）输入神经网络，回检结果如图9 所示。

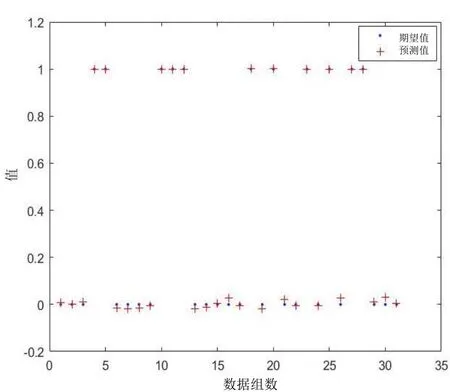
图9 模型回检结果

由图9 可知，31 组回检实验数据的其中第4、5、10、11、12、18、20、23、25、27、28 组结果接近1，为过车占用信号。其余20 组的结果接近0，为正常空闲信号，回检准确率为100%。

当神经网络回检完成后，为了验证神经网络对行车判断的准确性，再把20 组的实时测试数据集P2（其中包括4 组过车占用数据和16 组正常空闲数据）代入训练完成的神经网络，进行轨道电路行车信号判断实验验证。

对于模型的预测值，若大于等于0.5，记为1，表示为过车占用信号，小于0.5，记为0，表示为正常空闲信号，来检验结果是否为有效判断。具体判断结果如表2 所示。

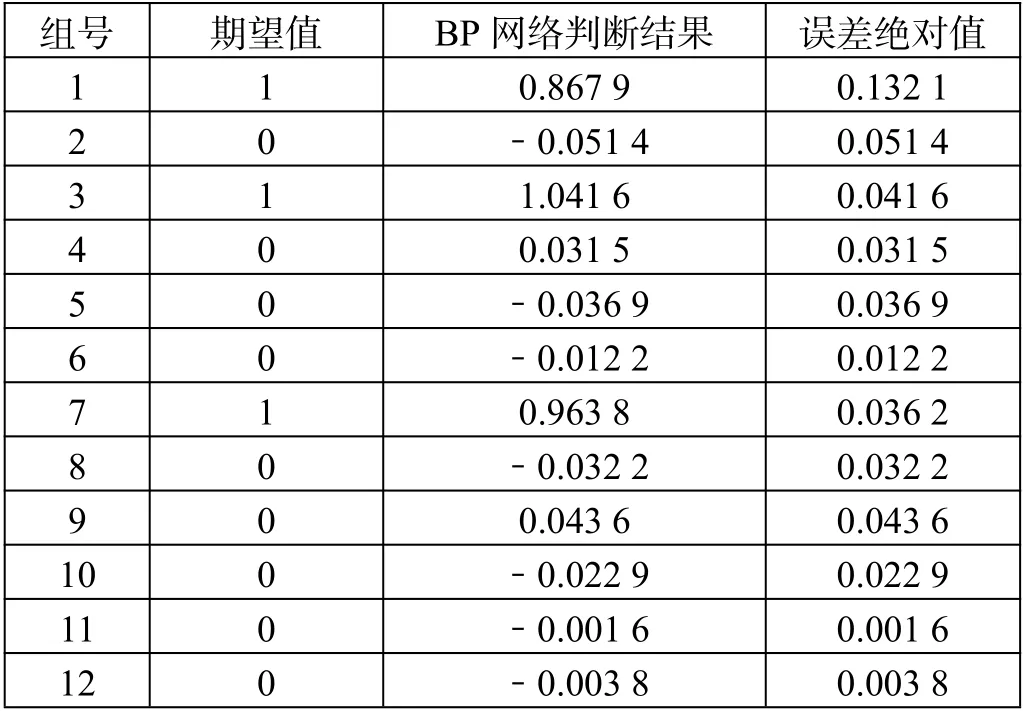
表2 模型测试结果

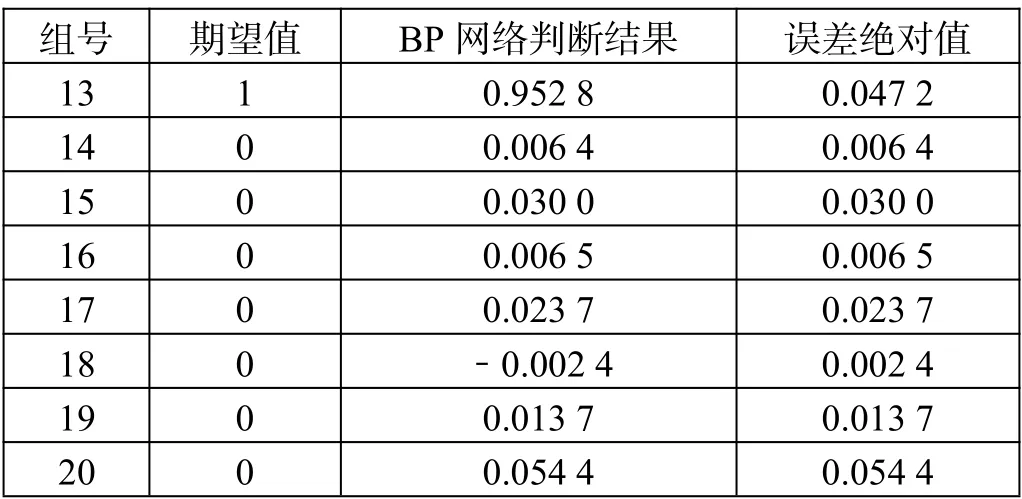
表2（续）

由表2 可知，20 组测试数据判断结果中第1、3、7、13 测试组的结果均大于0.5，记为1，即过车占用信号，其余16 组小于0.5，记为0，即正常空闲信号，判断准确率为100%。

5 基于RBF 神经网络的行车判断

径向基函数（RBF）神经网络是一种三层结构的前馈型人工神经网络，包括输入层、隐藏层和输出层。从输入层到隐藏层的是非线性变换，隐藏层的输出层是线性变换[14]。

RBF 神经网络需要求解的参数有基函数的中心、方差和隐藏层到输出层的权值。一般采用自组织选取学习中心方法，即第一步通过无监督学习过程求解隐藏层的基函数中心和方差，第二步通过有监督学习过程求解隐藏层到输出层的权值[15]。

RBF 神经网络的隐藏层节点采用输入模式与中心向量的距离（如欧式距离）作为函数的自变量，并使用径向基函数作为激活函数。神经元的输入离径向基函数中心越远，神经元的激活程度就越低。RBF 网络的输出与部分调参数有关，譬如，一个隐藏层输出值只影响一个输出层的输出值，因此具有“局部映射”特性。

本文调用径向基（RBF）神经网络语句net=newrb（P，T，goal，spread，mn，df），设置目标误差goal为10-6，初始常数spread 设置为1，最大神经元个数mn 为20，df 为1，表示每增加1 个神经元显示一次结果，通过行车判断实验发现当spread 常数为1 和2 时，对正常信号可有效判断，而对过车信号无法正确判断，准确率分别为80%和90%，当大于等于3 时，准确率均为100%；当spread 常数为3 时，神经元个数增加到12 个时达到目标误差算法停止，判断结果如表3 所示。

由表3 可知，RBF 网络20 组测试数据判断结果中第4、13、16、17 测试组的结果均大于0.5，记为1，即过车占用信号，其余16 组小于0.5，记为0，即正常空闲信号，判断准确率为100%。

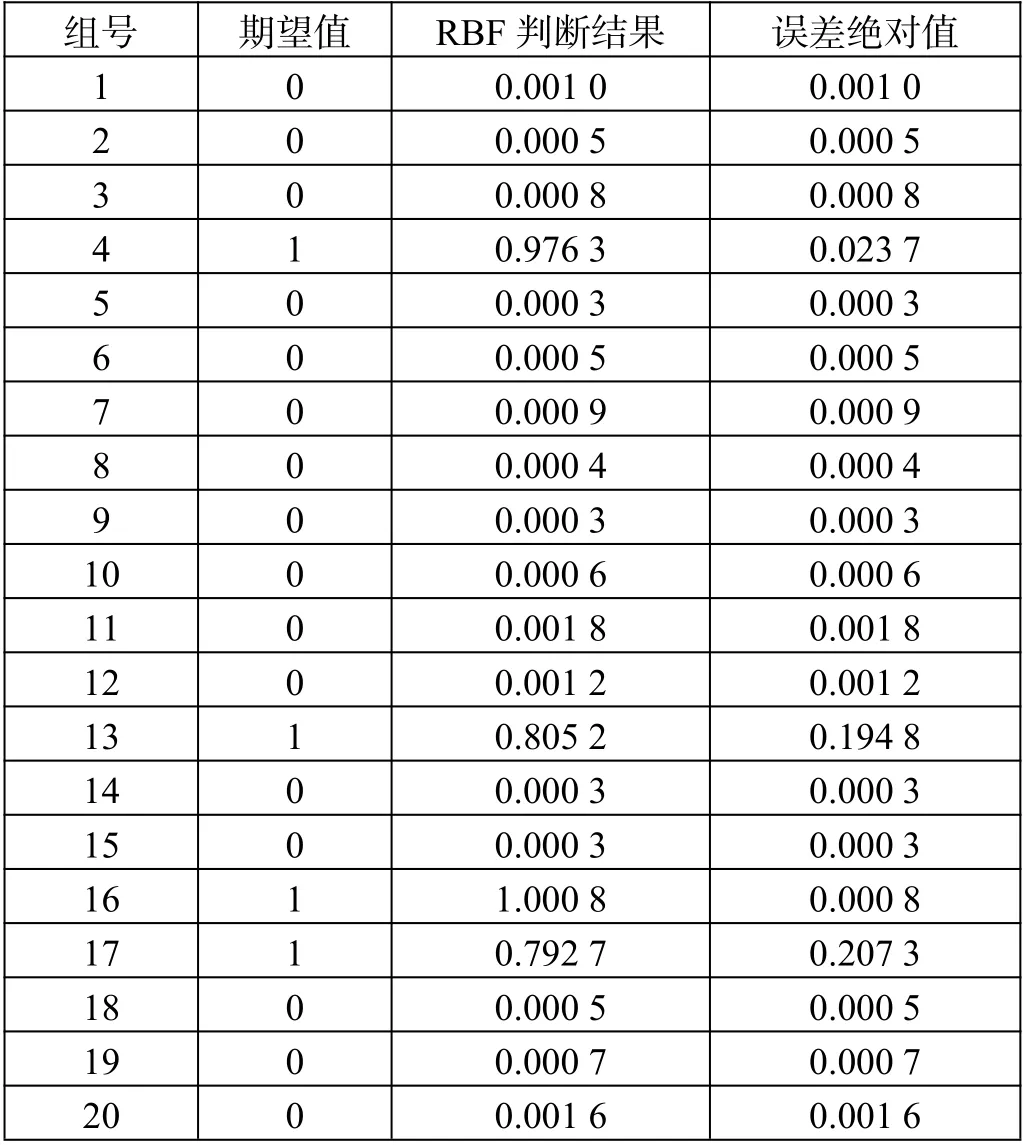
表3 RBF 模型判断结果

6 结语

本文为了解决ZPW-2000R 型轨道电路系统中行车信号的实时判断问题，研究了基于BP 和RBF 神经网络的智能判断方法。

以轨道电路系统主接收器的主机调接入电压为输入，列车运行状态为输出，将实验采集的不同维度的实时数据补齐至相同的维度后作为神经网络训练的输入，并用MATLAB 软件编写算法程序，通过实验来确定模型隐藏层神经元个数、学习率、动量因子等相关参数，不断训练和优化网络模型，并对模型进行回检验证实验，分别建立了BP 和RBF 神经网络模型。

将测试数据代入训练好的模型对轨道电路行车信号进行判断，实验结果表明，本文提出的基于BP 和RBF 神经网络的智能判断方法对轨道电路主机调接入电压行车信号判断准确率均达到100%，从而为实际轨道电路中利用主机主接入电压和主机调接入电压信号联合判断轨道占用状态和空闲状态提供了一种智能方法。