Saber 算法的多项式乘法FPGA 实现研究*

范建南 高献伟 薛文瀚

北京电子科技学院，北京市 100070

1 引言

为了抵抗量子算法的攻击，美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）于2016 年正式启动了后量子密码标准征集［1］。 经过三轮激烈的竞争，基于格结构的Saber 算法凭借带宽低、灵活性高等特点［2］，成为最终7 种候选算法之一。 Saber 算法具有较为独特的参数集设计，其模数n为2 的整数次幂，非常适合硬件实现。 许多学者正努力对Saber 算法进行硬件高效实现，以促进Saber 算法设计方案的不断完善，从而影响后量子密码的标准化进程。

文献［3］对基于格的后量子密码算法展开了全面的调查研究，指出基于格的后量子密码算法有两大关键问题，分别是多项式乘法与离散高斯采样。 作为Saber 算法的核心部件，多项式乘法成为了算法实现的主要加速瓶颈。 近年来，国内外有多个团队使用不同方法对多项式乘法进行硬件实现研究。 文献［4］提出了格密码的一种指令集协处理器结构，并实现了高度并行的schoolbook 多项式乘法器，只需要256 个循环便能计算1 次多项式乘法，但会消耗大量的硬件逻辑资源。 文献［5］在Saber 算法的高速SW／HW代码设计中，使用256 个带13 位输入的DSP（digital signal process，数字信号处理）单元设计了基于schoolbook 的乘法器。 文献［6］针对现有的SPMA（schoolbook polynomial multiplication algorithm） 结构， 提出了一种优化的 SPMAKaratsuba 结构，以92.06%的额外硬件开销，获得了2.09 倍的速度。 清华大学团队采用8 级分层Karatsuba 算法实现多项式乘法，降低了面积开销［7］。 文献［8］在软硬件协同实现中，设计了一种基于Toom-Cook 算法的Saber 乘法器。 文献［9］在实现NTRU 算法非3－系数多项式乘法时，采用Toom-Cook-3 way 算法将一个n系数多项式乘法拆分为5 个n／3 系数乘法，然后使用5个奇偶Karatsuba 乘法器对n／3 系数乘法并行计算。

为了进一步提高硬件实现的效率，本文在分析schoolbook 算法、Karatsuba 算法、Toom-Cook算法基础上，融合这三种方法，针对Saber 算法中的256×256 多项式乘法，提出五种基于Toom-Cook 算法的多项式乘法改进方案，并完成改进方案的FPGA（field programmable gate array，现场可编程门阵列）设计，在通过功能仿真的基础上，使用具有自主知识产权的国产FPGA 芯片进行综合，对五种方案的性能进行严谨的分析比较，找到了Saber 算法中高效实现多项式乘法运算的一种设计方法。

2 多项式乘法

2.1 Saber 算法的多项式乘法

Saber 算法具有三个参数集，分别对应不同的安全等级。 对于任意参数集，所有的运算都在环Z q［x］／（xn ＋1） 上进行。 其中，阶数n ＝256表示多项式中变量的最高次数为255，即每个多项式都有256 个系数，模数q ＝213表示多项式的每个系数都有13 位，模数的如此设计能够避免模约减运算，便于算法的硬件实现。 实现多项式乘法的方法很多，目前最快的算法是快速数论变换（number theoretic transforms，NTT），然而，使用NTT 算法要求模数必须为素数［10］，对于模数q ＝213的Saber 算法并不适用。 因此，考虑使用算法复杂度略高的常用方法，在优化改进后实现Saber 算法的多项式乘法。

2.2 经典schoolbook 多项式乘法算法

对于Saber 算法中的256×256 多项式乘法运算，一个简单易行的方法为schoolbook 算法。事实上，schoolbook 算法属于传统的乘法运算方法，经过2 层的嵌套迭代，共计256×256 次乘法运算，便可求得最终结果。 算法1 给出了该算法的详细描述，对于具有256 个系数的多项式a与多项式b的乘法运算，多项式a的第1 个系数a0经过第1 层256 次迭代，分别乘以多项式b的256 个系数b0……b255，在第2 层循环迭代中依次将多项式a的剩余系数a1……a255重复执行第1 层运算操作，然后与对应位置的中间值进行累加，取模后完成256×256 次乘法运算。 对于n阶多项式乘法运算，采用schoolbook 算法具有二次复杂度n2， 单一地使用全并行schoolbook 算法实现256×256 多项式乘法运算将消耗大量的硬件资源。

算法1：schoolbook 求解256×256 多项式乘法输入：阶数为256 的多项式a阶数为256 的多项式b输出：阶数为511 的多项式c计算过程：1. for i ＝0 to 255 do 2. for j ＝0 to 255 do 3. c［i ＋j］ ＋＝a［i］·b［j］mod（213） ；4. return c

2.3 基于Karatsuba 的多项式乘法算法

Karatsuba 算法是由A. Karatsuba 于1960 年发现的一种快速乘算法［11］，该算法采用“分治”思想，通过循环递归将多项式乘法运算逐步二分拆解，直至拆解后的最小运算单元结构简单、易于求解，再进行小数乘法，并重组所乘的全部中间值，求得多项式乘法运算的最终结果。

以计算A（x）× B（x） 为例，假设A（x） 和B（x） 是环Z q［x］／（xn ＋1） 上的两个n阶多项式，分别取A（x）＝an－1xn－1＋…＋a1x ＋a0，B（x）＝bn－1xn－1＋…＋b1x ＋b0。 阶数n可能为素数，而Karatsuba 算法的“分治”思想要求n为2 的整数次幂。 如果n是2 的整数次幂，则直接使用Karatsuba 算法；如果n不是2 的整数次幂，则可以通过给高位系数补上若干个“0”，使得新的阶数nnew变成2 的整数次幂。 对于后量子Saber 算法，其阶数n ＝256，恰好是2 的整数次幂，可直接使用Karatsuba 算法进行迭代计算。

使用Karatsuba 算法计算A（x）× B（x） 时，首先将多项式A（x）、B（x） 直接拆分为两部分，即：

总共需要四组乘法才能完成运算，而Karatsuba 算法巧妙地通过增加加法和减法运算，减少了乘法运算，求解表达式如式（3）所示。

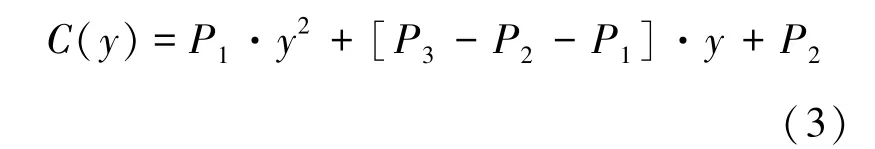
其中，P1、P2、P3分别由式（4）、（5）、（6）共三组乘法计算得来。

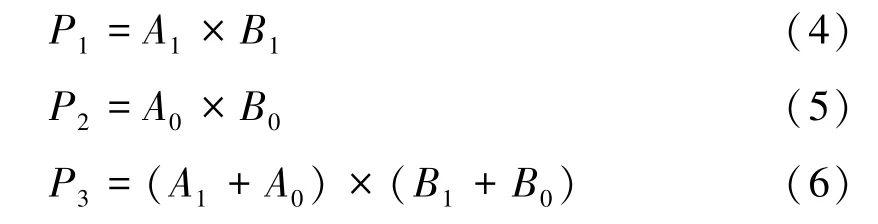
相较于式（2）中的经典方法，Karatsuba 算法减少了一组乘法运算。

图1 以aw1× bw1为例，给出了Karatsuba 算法的原理框图。

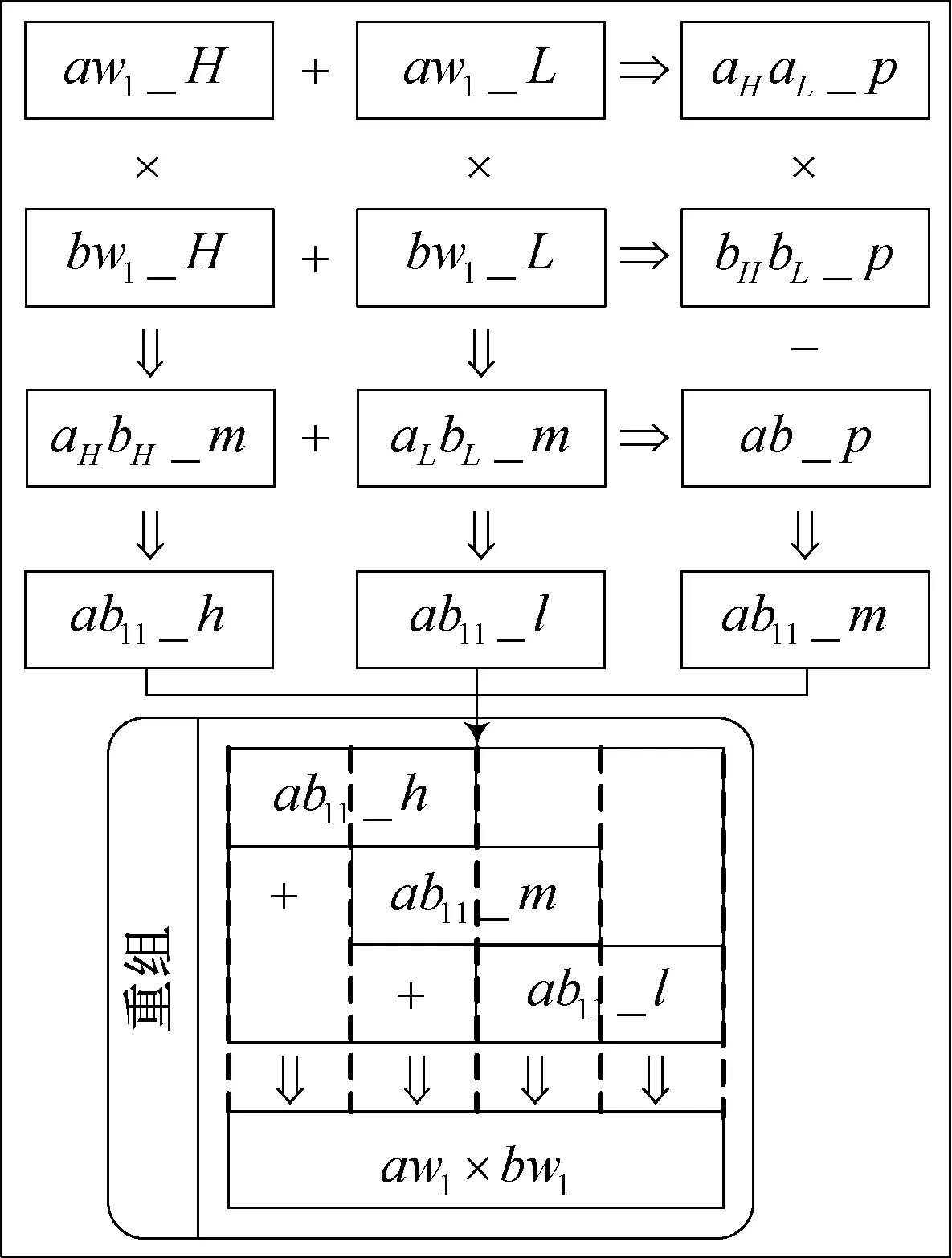
图1 Karatsuba 算法的原理框图

首先，将aw1和bw1分别拆分为长度相等的两部分aw1＿H、aw1＿L及bw1＿H、bw1＿L， 然后分别将aw1及bw1的高低两部分相加得到中间量aHaL＿p及bHbL＿p，使用三次乘法运算将对应部分相乘，其中，中间量的乘积结果ab＿p减去另外两部分的乘积结果，得到ab11＿h、ab11＿l及ab11＿m后，经移位重组求得最终的乘法运算结果。 算法2 给出了使用Karatsuba 算法求解2n ×2n多项式乘法的详细步骤，其中，图1 中的重组过程即为算法2 中第11 行的移位加法操作。 算法中的RM（recursive multiplication）表示子多项式的迭代乘法运算，通过调用下一轮的Karatsuba 算法，计算更小单元的多项式乘法。 算法2 中第7－10行便是使用若干轮的RM 运算进行子多项式迭代乘法，计算得到的结果ab＿L、ab＿H、ab＿M即为图1 中的运算中间值ab11＿l、ab11＿h、ab11＿m。

算法2：Karatsuba 求解2n × 2n 多项式乘法输入：阶数为2n 的多项式a阶数为2n 的多项式b输出：阶数为4n－ 1 的多项式c计算过程：

算法2：Karatsuba 求解2n × 2n 多项式乘法1. a＿L ＝a［n－ 1 ∶0］ ；2. a＿H ＝a［2n－ 1：n］ ；3. b＿L ＝b［n－ 1 ∶0］ ；4. b＿H ＝b［2n－ 1：n］ ；5. a＿P［n－ 1 ∶0］ ＝a＿H ＋a＿L；6. b＿P［n－ 1 ∶0］ ＝b＿H ＋b＿L；7. ab＿L［2n－ 2 ∶0］ ＝RM（a＿L，b＿L） ；8. ab＿H［2n－ 2 ∶0］ ＝RM（a＿H，b＿H） ；9. ab＿P［2n－ 2 ∶0］ ＝RM（a＿P，b＿P） ；10. ab＿M［2n－ 2 ∶0］ ＝ab＿P－ab＿L－ab＿H；11. c［4n－2∶0］ ＝（ab＿H≪2n） ＋（ab＿M≪n） ＋ab＿L；12. return c说明：每步计算完成后都进行mod（213） 约减操作

因此，对于2n ×2n的多项式乘法，1 轮Karatsuba 算法便可将其转化为3 个n × n乘法，减少了开销较大的乘法运算。 那么，对于Saber 算法的256×256 多项式乘法运算，使用8 轮Karatsuba 算法循环迭代就能将其转化为最小单元的乘法运算。 使用Karatsuba 算法计算长度为n的多项式乘法，k轮迭代的示意图如图2 所示。

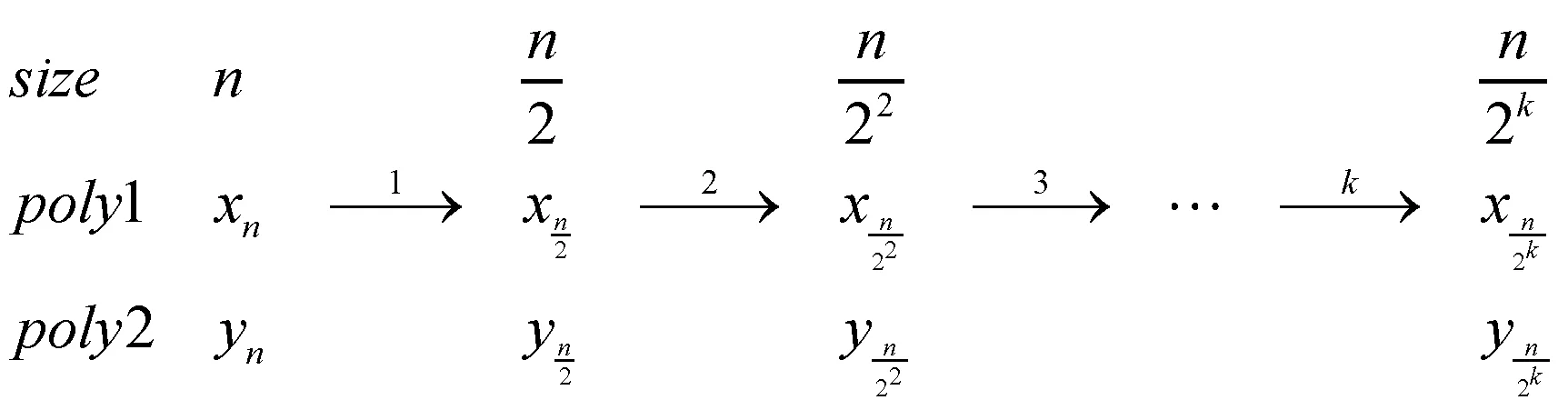
图2 Karatsuba 算法k 轮迭代示意图

Karatsuba 算法将长度为n的多项式进行迭代二分，每迭代一轮，长度缩短一半。 经过k轮循环迭代，长度变为n／2k。 如果将多项式迭代二分为最小的单数乘法，即n／2k ＝1， 则k ＝log2n，总共需要log2n轮迭代二分。 每轮Karatsuba 算法迭代，都巧妙地用3 次乘法运算代替4次乘法运算。 那么，k轮迭代后，算法的时间复杂度计算推导如式（7），Karatsuba 算法的时间复杂度为n1.585， 这比schoolbook 算法的二次复杂度更优。

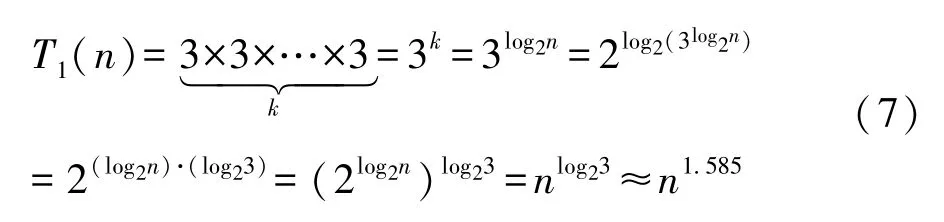
2.4 基于Toom-Cook 的多项式乘法算法

Toom-Cook 算法是Karatsuba 算法的更快推广［12］，Karatsuba 算法可以看做Toom-Cook-k way在k ＝2 时的一种特例，其本质都是利用了“分治”思想。 实际上，Toom-Cook-k way 算法由“拆分”、“评估”、“迭代乘法”、“插值”、“重组”五个步骤组成［13］。 对于两个阶数为n的多项式，Toom-Cook-k way 算法分别将其拆分为k个子多项式，在2k－1 个点上进行逐点评估，再将两个多项式的评估值进行逐点乘法，随后经过插值求解出2k－1 组中间值，最后移位重组得到两个多项式的乘法运算结果。 其中，k的取值较为灵活，如果k值取得较小，无法减小算法的时间复杂度，但k值取得较大，会增加评估及插值过程中的复杂计算。 综合考虑Saber 算法的参数集特性，我们决定基于Toom-Cook-4 way 进行算法改进设计。 因此，下面给出Toom-Cook-4 way 求解n ×n多项式乘法A（x）×B（x） 五个步骤的具体描述。

2）评估：在7 个点上对式（8）中的多项式A（y）、B（y） 逐点评估，即将7 个点的值分别带入A（y）、B（y） 的表达式，求得7 组评估结果。为了尽可能减少乘法运算，进一步提高运算效率，选取y ＝｛0，±1／2，±1，2，∞｝ 作为评估的7个点。 此时，评估过程中的乘法因子要么是计算简单的0、±1、∞，要么是2 的整数次幂，这可通过简单的移位操作实现。 式（9）给出对多项式A（x） 进行评估的表达式，多项式B（x） 的评估表达式与此类似。

4）插值：与评估相反，插值是求解7 个线性无关的方程组，在y ＝｛0，±1／2，±1，2，∞｝ 上，根据式（10）与式（11）可以得到C（y） 的7 组迭代乘法值与各组系数C0、C1、C2、C3、C4、C5、C6的关系如下：

此时，对上述矩阵关系进行变形，可得：

求出式（13）中系数矩阵的逆，可得：

其中，步骤3）的迭代乘法运算，可通过Toom-Cook-4 way 算法对子多项式乘法进行若干轮循环迭代，将宽系数乘法转化为窄系数乘法，宽系数乘法为含有较多系数的多项式乘法，窄系数乘法为含有较少系数的多项式乘法，窄系数乘法的计算复杂度优于宽系数乘法。 在Toom-Cook-4 way 算法步骤中，每经过1 轮循环迭代，多项式的阶数便降为原来的四分之一。 Saber 算法中乘法多项式的阶数n ＝256，恰好为4 的4次幂，那么，对于Saber 算法中的256×256 多项式乘法，经过4 轮Toom-Cook-4 way 算法循环迭代，即可转化为最小的单数乘法，进而求得最终结果。 上述五个步骤中，插值过程较为复杂［14］，算法3 根据插值公式（14），结合步骤5）的移位累加思路，给出了Toom-Cook-4 way 算法求解256×256 多项式乘法时插值与重组过程的伪代码。

算法3：Toom-Cook-4 way 算法的插值与重组输入：含有127 个系数的7 个数组w1 至w7输出：含有511 个系数的数组c计算过程：／ ／插值过程1. for i ＝0 to 126 do 2. r1 ＝w1［i］；r2 ＝w2［i］；r3 ＝w3［i］ ；3. r4 ＝w4［i］；r5 ＝w5［i］；r6 ＝w6［i］ ；4. r7 ＝w7［i］；r2 ＝r2 ＋r5；r6 ＝r6－r5；5. r4 ＝（（r4－r3） ＞＞1） ；6. r5 ＝（（r5－r1－ （r7 ＜＜6）） ＜＜1） ＋r6；7. r3 ＝r3 ＋r4；r2 ＝r2－ （r3 ＜＜6）－r3；8. r3 ＝r3－r7－r1；r2 ＝r2 ＋45*r3；9. r5 ＝（（（r5－ （r3 ＜＜3））*43691） ＞＞3） ；10. r6 ＝r6 ＋r2；r3 ＝r3－r5；11. r2 ＝（（（r2 ＋（r4 ＜＜4））*36409） ＞＞1） ；12. r6 ＝（（（（30*r2）－r6）*61167） ＞＞2） ；13. r4 ＝－ （r4 ＋r2）；r2 ＝r2－r6；／ ／重组过程14. c［i］ ＋＝r7；c［i ＋64］ ＋＝r6；c［i ＋128］ ＋＝r5；15. c［i ＋192］ ＋＝r4；c［i ＋256］ ＋＝r3；16. c［i ＋320］ ＋＝r2；c［i ＋384］ ＋＝r1；17.return c说明：每步计算完成后都进行mod（213） 约减操作

在算法插值过程中，除了乘法、加法和减法外，需特别关注除法运算。 当除以一个奇数时，就相当于乘以该奇数在mod（213） 下的逆，算法3 第9、11、12 行的数值43691、36409、61167 分别是乘数因子3、9、15 在mod（213） 下的逆；当除以2 的整数次幂时，相当于进行右移操作，右移操作可能会造成精度的损失，从而导致结果的错误。 整个Toom-Cook-4 way 算法的计算过程最多右移3 位，为了保证结果的正确性，需额外3位的精度，算法设计的数据位宽最少应为16位［8］。 使用Toom-Cook-4 way 算法计算长度为n的多项式乘法，进行k轮迭代的示意图如图3所示。

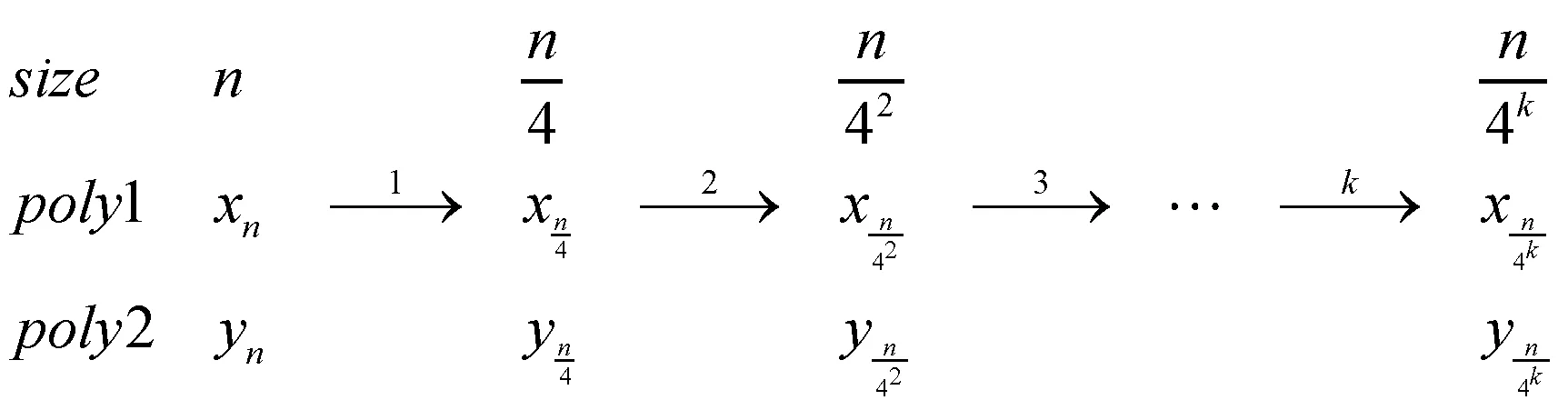
图3 Toom-Cook-4 way 算法k 轮迭代示意图

Toom-Cook-4 way 算法将长度为n的多项式进行迭代运算，每迭代一轮将其拆分为7 次乘法，长度缩短为原来的四分之一。 经过k轮迭代，长度变为n／4k，如果将多项式迭代为最小的单数乘法，即n／4k ＝1，那么，k ＝log4n ＝（1／2）·log2n，总共需要（1／2）·log2n轮迭代。k轮迭代后，算法的时间复杂度计算推导如下：

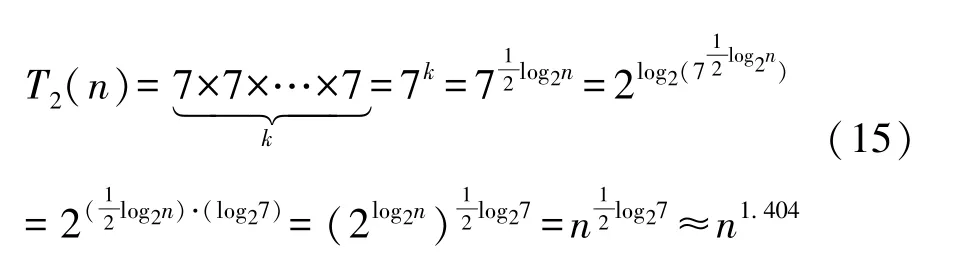
3 基于Toom-Cook 的多项式乘法算法改进方案

Toom-Cook 算法相较于经典schoolbook 算法及Karatsuba 算法，具有更低的时间复杂度。 但插值、重组等过程引入了乘法及较多的加减法运算，对于阶数n ＝256 的多项式乘法并没有带来最优的实现效果。 本文结合第2 章中介绍的Karatsuba 算法及经典schoolbook 算法，设计一种基于Toom-Cook 的多项式乘法算法改进方案。设计的基本思想是使用1 轮Toom-Cook-4 way 算法，加上若干轮Karatsuba 算法循环迭代，底层调用schoolbook 算法，高效完成多项式乘法运算，该设计的关键问题是确定Karatsuba 算法的迭代轮数。 根据章节2.3 中的分析，Karatsuba 算法通过增加简单的加减法运算减少复杂的乘法运算，但是随着迭代轮数的增加，大量增加的加减法运算并不能起到加速多项式乘法运算的效果。找到合适的Karatsuba 算法迭代轮数，对高效实现整个256×256 多项式乘法尤为重要。

该设计方法的原理如图4 所示，首先使用1轮Toom-Cook-4 way 算法，将阶数为256 的多项式A（x） 与多项式B（x） 拆分为四部分，每一部分的阶数为64，在7 个点y ＝｛0，±1／2，±1，2，∞｝ 上分别对其进行逐点评估，将256×256 多项式乘法转化为7 个64×64 多项式乘法，再使用若干轮Karatsuba 算法对64×64 多项式乘法进一步二分拆解，每迭代一轮，长度缩短一半。 在Karatsuba 算法迭代过程中，不断调用schoolbook 算法进行全乘。 将迭代乘法所得的7 组中间值（每组含有127 个系数），利用插值求出C（x） 的7 组系数，然后经移位重组得到含有511 个系数的多项式乘法运算结果C（x）。

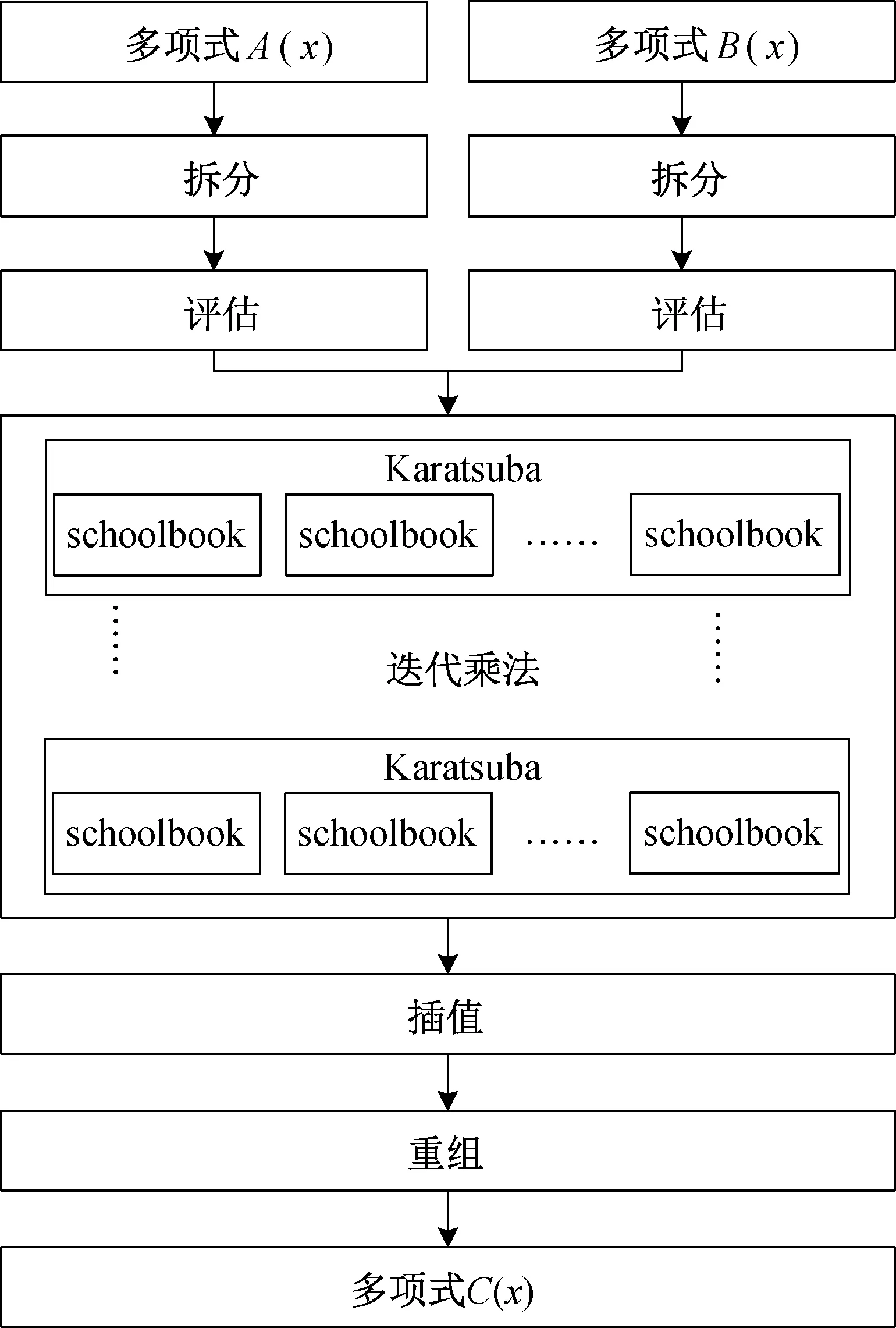
图4 基于Toom-Cook 算法的改进型设计原理图

由于该多项式乘法是在环Z213［x］／（x256＋1） 上进行的，还需额外进行mod（x256＋1） 约减，得到含有256 个系数（每个系数含有13 位）的多项式乘法最终结果C′（x）。

考虑到Karatsuba 算法迭代轮数能决定整个改进型设计方法的效率，因此根据Karatsuba 算法迭代轮数的不同，可得到下面五种设计方案。

方案1 ∶1 轮Toom-Cook-4 way 算法＋1 轮Karatsuba 算法＋schoolbook 算法32×32 全乘。使用1 轮Toom-Cook-4 way 算法将256×256 算法转化为7 个64×64 多项式乘法，然后使用1 轮Karatsuba 算法，将每1 个64×64 多项式乘法转化为3 个32×32 多项式乘法，随后直接调用schoolbook 算法完成32×32 多项式乘法运算；

方案2 ∶1 轮Toom-Cook-4 way 算法＋2 轮Karatsuba 算法＋schoolbook 算法16×16 全乘。与方案1 类似，增加1 轮Karatsuba 算法迭代，在计算32 × 32 多项式乘法时， 再使用1 轮Karatsuba 算法，将每1 个32×32 多项式乘法转化为3 个16×16 多项式乘法，随后直接调用schoolbook 算法完成16×16 多项式乘法运算；

方案3 ∶1 轮Toom-Cook-4 way 算法＋3 轮Karatsuba 算法＋schoolbook 算法8×8 全乘。 在方案2 基础上，使用第3 轮Karatsuba 算法将每1个16×16 多项式乘法转化为3 个8×8 多项式乘法，随后直接调用schoolbook 算法完成8×8 多项式乘法运算；

方案4 ∶1 轮Toom-Cook-4 way 算法＋4 轮Karatsuba 算法＋schoolbook 算法4×4 全乘。 在方案3 基础上，再使用1 轮Karatsuba 算法将每1个8×8 多项式乘法转化为3 个4×4 多项式乘法，随后直接调用schoolbook 算法完成4×4 多项式乘法运算；

方案5 ∶1 轮Toom-Cook-4 way 算法＋5 轮Karatsuba 算法＋schoolbook 算法2×2 全乘。 在方案4 基础上，再使用1 轮Karatsuba 算法将每1个4×4 多项式乘法转化为3 个2×2 多项式乘法，随后直接调用schoolbook 算法完成2×2 多项式乘法运算；

这五种方案相似，只是Karatsuba 算法迭代轮数不同。 Karatsuba 算法本身是一种天然的迭代算法，在本设计中，为了计算7 个64×64 多项式乘法，需要重复调用Karatsuba 算法，Karatsuba算法的每次循环迭代结构相似、操作相同。 根据这一特性，采用循环迭代设计方法，如图5 所示，即一个时钟周期调用1 次Karatsuba 算法。 以方案2 为例，进行2 轮Karatsuba 算法迭代，每轮重复调用3 次Karatsuba 算法，总共需要9（3×3）个时钟周期。 那么，对于Toom-Cook-4 way 中的迭代乘法过程，也只需要63（7×3×3）个时钟周期，便可调用到最底层的schoolbook 算法计算16×16 多项式乘法。 该设计方法的特点是通过循环迭代复用运算单元，减少硬件资源的消耗，尽管在一定程度上会降低计算速度，但由于迭代轮数并不多，所消耗的时钟周期增加的并不明显，能够达到较佳的实现效果。

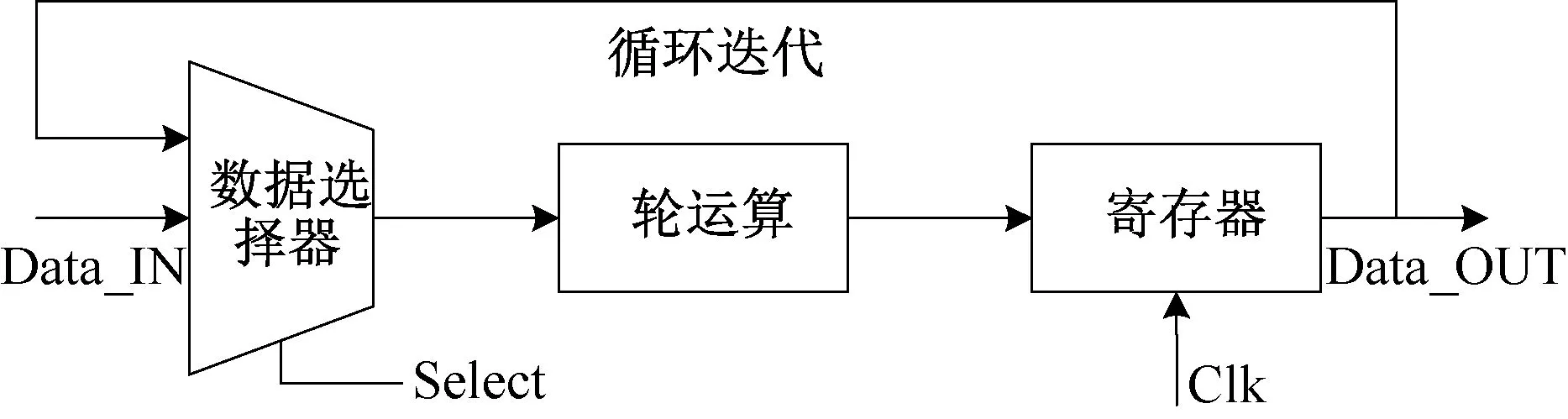
图5 循环迭代设计方法

底层的schoolbook 算法复杂度相对较高，但处理的乘法为窄系数多项式乘法，考虑到该算法需要被上层多次调用，为了加速整个融合算法，底层schoolbook 算法采用并行循环迭代结构，如图6所示。 对于调用schoolbook 算法计算n × n的多项式乘法，使用n个并行的乘法运算单元，1 个时钟周期迭代1 轮，每轮并行完成n个乘法运算，经过n个时钟周期，便可完成全部n × n乘法运算，既不会消耗过多的硬件资源，也能减少时钟周期。

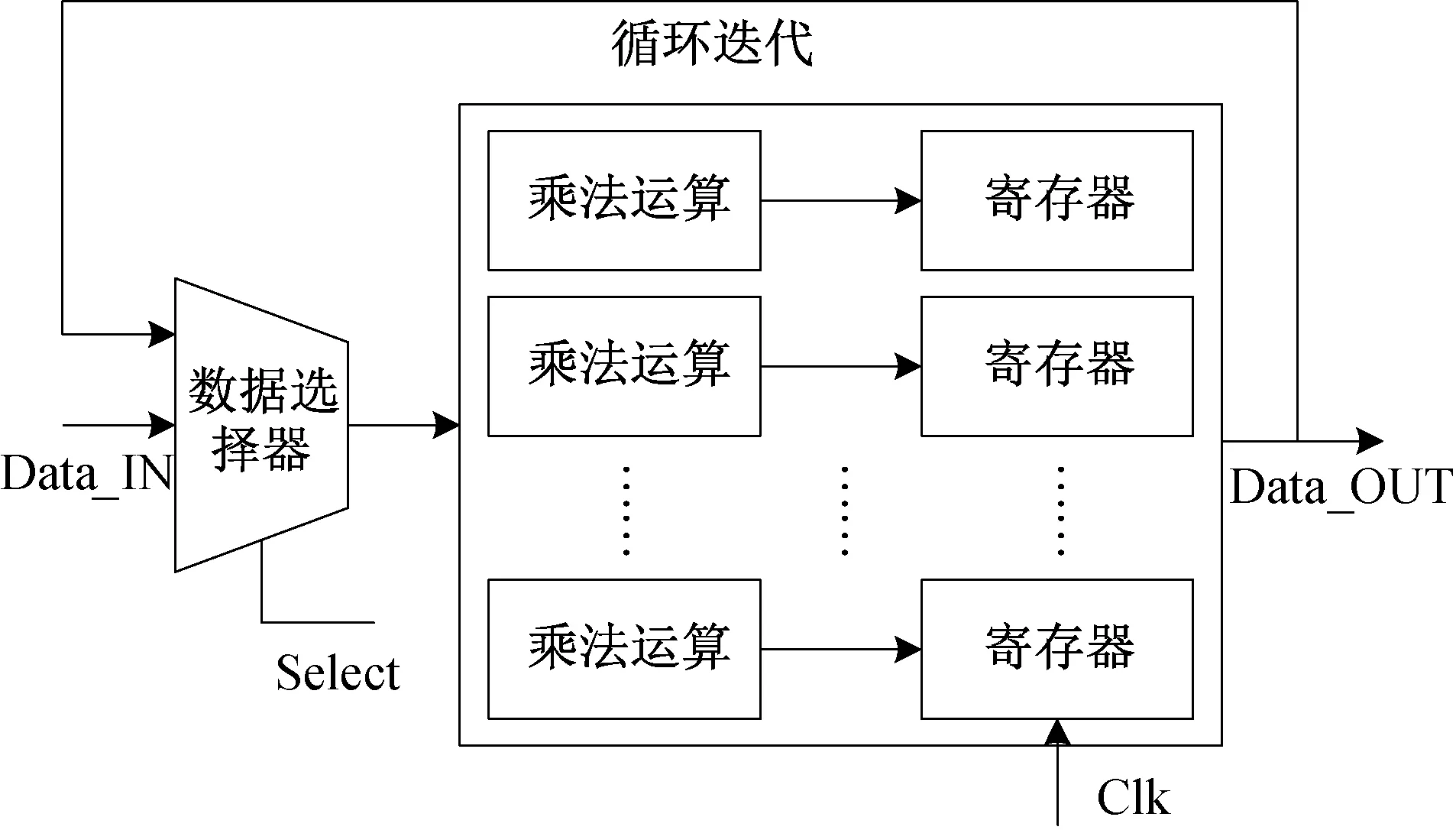
图6 并行循环迭代设计方法

4 仿真结果与性能分析

4.1 仿真结果

对于本文所设计的基于Toom-Cook 的多项式乘法算法改进方案，采用Verilog HDL 对五种设计方案进行编程，并在Modelsim SE 10.2c 中进行了多组数据的仿真实验，验证了其正确性。其中一组数据的仿真结果如图7 所示，从仿真时间点t ＝0.01ns 开始运算（EndFlag 由无效值跳变为0），经过7.63ns 的计算，在仿真时间点t ＝7.64ns 结束运算（EndFlag 由0 跳变为1），得到多项式乘法的最终运算结果。 对于Saber 算法中的256×256 多项式乘法运算，随机生成若干组含有256 个系数的多项式a与多项式b，每个系数含有13 位，将其分别存放在256×16 的向量中，输入算法后经过计算得到长度为256×13 的多项式c。 我们对多组随机多项式的乘法运算进行了仿真，并调用Saber 算法公开的C 源码对这些多项式乘法进行验算，所求结果皆与本设计的仿真结果一致，验证了本设计的正确性。

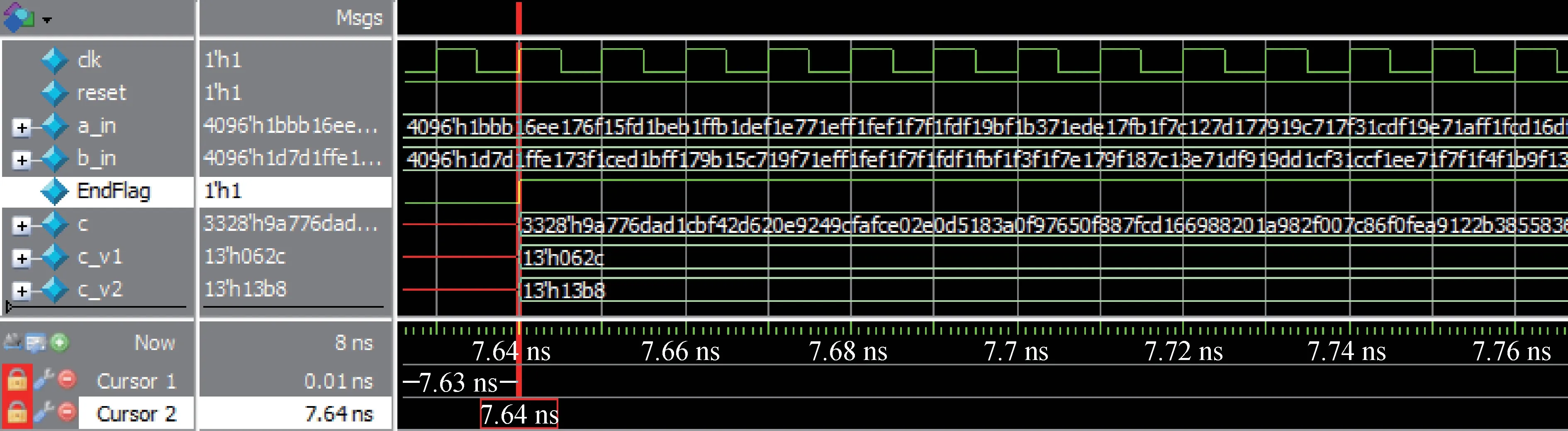
图7 256×256 多项式乘法的运算结果

4.2 基于国产FPGA 的多项式乘法改进方案性能分析

在对设计方案完成功能仿真后，为了更好评估算法性能，从五种方案中找出较为高效的多项式乘法运算方法，可进一步对其进行分析综合。当前，国家正大力推进芯片产业振兴发展，许多优质的国产芯片、国产平台应运而生。 本文选择深圳紫光同创电子有限公司开发的FPGA 设计平台Pango Design Suite，FPGA 器件选择该公司设计的Titan 系列。 作为中国第一款具有自主知识产权的千万门级高性能FPGA 产品，Titan 系列采用了具有成熟工艺和自主产权的体系结构。我们选用的器件是Titan 系列PGT180H－7FFBG676，该器件有145016 个LUT（look-up tables，查找表），217524 个FF（flip flop，触发器），以及224 个APM（arithmetic process module，算术处理单元）。 在Pango Design Suite 上使用该器件对五种设计方案进行综合，表1 给出了不同设计方案的性能分析。

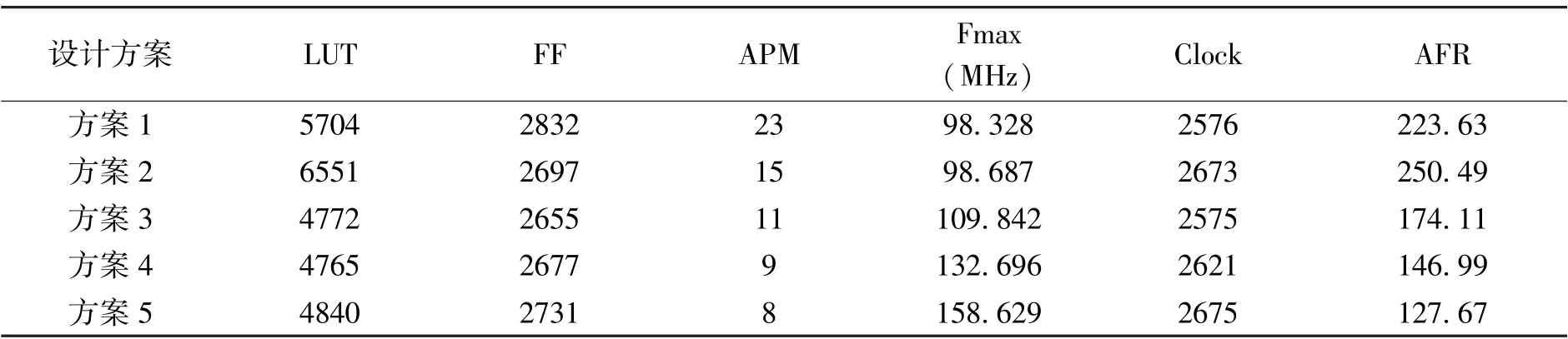
表1 五种多项式乘法设计方案的性能分析

主要的性能指标为算法所使用的基本逻辑单元LUT、FF 和算术处理单元APM，以及算法运行的最高频率Fmax 和时钟数Clock，不同设计方案的这五个性能指标数据都已在表1 中列出。 FPGA 设计主要目标是高速度或小面积，为了得到一个最优的速度与面积的折中方案，本文采用性能指标AFR（area-frequency ratio，面频比率），该指标的计算公式为：

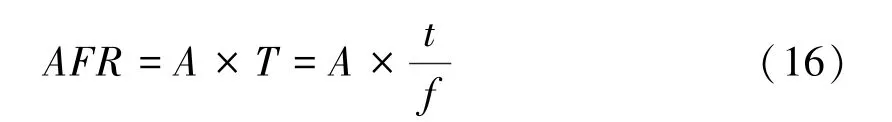
A 为占用的硬件资源面积，包含LUT、FF 等基本逻辑单元的数目；T ＝t／f表示算法运行一次所需要的时间，其中，t为使用的时钟数目，f为算法运行的最高频率。 面频比率AFR 越小，则说明占用的硬件资源面积小且运行速度快，这是FPGA 设计所追求的目标。 综合分析可知，方案1 与方案2 由于Karatsuba 迭代轮数少，直接调用底层schoolbook 算法进行较宽系数的全乘运算，一方面会使用较多的算术处理模块APM，且耗费更多的硬件逻辑资源，另一方面也会拖慢算法运行速度，性能表现并不佳。 方案3、4、5 所使用的逻辑资源相差不大，主要区别体现在运行速度上，随着Karatsuba 算法迭代轮数的增加，算法运行所能达到的最高频率也不断增大，对比发现，方案5 使用的LUT 及FF 数目虽然比方案3及方案4 更多一些，但其面频比率AFR 更小，运行速度更快，且使用了更少的算术处理模块，是五种方案中最佳的多项式乘法设计方案。

为了更好地评估方案5 的算法性能，将其与其他文献的实现方法进行对比分析。 文献［9］使用经典schoolbook 算法实现了Saber 算法256×256 多项式乘法，最高频率达到370MHz，且只需要256 个Clock，实现了算法运行的高速度，但却消耗了11426 个LUT 及8727 个FF，占用了较多的硬件逻辑资源。 文献［6］结合Karatsuba 算法与schoolbook 算法，实现了后量子R-LWE（ring-learning with error，环错误学习）算法（参数选择为n＝256、q＝7681）的多项式乘法，仅使用了1125 个LUT 及1034 个FF，且最高频率为335.8MHz，但完成一次运算却需要8787 个Clock。 对比发现，本文设计的方案5，虽然没有文献［9］的高速度，也没有文献［6］的低面积，却弥补了上述两种方法的缺陷，找到了速度与面积的平衡折中，在使用较少的硬件资源下，达到了较快的运算速度。 因此，后量子Saber 算法在进行256×256 多项式乘法时，较高效的算法是使用1 轮Toom-Cook-4 way 算法结合5 轮Karatsuba算法及schoolbook 算法2×2 全乘。

5 结束语

本文针对后量子Saber 算法的核心部件多项式乘法运算，结合Karatsuba 算法及经典schoolbook 算法，提出了五种基于Toom-Cook 的多项式乘法算法改进方案，并在国产FPGA 开发平台Pango Design Suite 上进行了Verilog HDL设计，核心部分采用循环迭代方法实现结构优化。 最后，使用Modelsim SE 10.2c 对五种方案的硬件设计进行功能仿真，并在国产FPGA 器件上进行了分析综合。 为了较好地衡量运行速度与硬件逻辑资源之间的关系，引入性能指标——面频比率AFR。 从综合结果来看：随着改进方案中Karatsuba 算法迭代轮数的增加，所耗费的硬件资源相对稳定，乘法运算的速度却有明显加快，面频比率AFR 逐渐减小，性能不断优化。 相较于经典的单一多项式乘法运算方法，将1 轮Toom-Cook-4 way 算法与5 轮Karatsuba 算法及schoolbook 算法2×2 全乘结合起来，具有较为明显的优势。 后续打算进一步优化提升乘法的速度，将该多项式乘法方法应用于后量子Saber 算法具体实现中，并推广至NIST 第三轮后量子密码标准征集中的其他候选算法，对后量子算法的硬件实现起到加速作用。