一种基于搜索历史信息的粒子群算法

李子旭,吴凌宇,葛婉贞,赵新超

(北京邮电大学 理学院,北京 100876)

0 引言

粒子群算法(Particle Swarm Optimization,PSO)是1995年由Kennedy和Eberhart在文献[1]中提出。它是一种以群体智能为基础的随机搜索算法。该算法以没有质量、没有体积的粒子作为个体,模拟自然界鸟群搜索食物的行为方式,用以求解优化问题。文献[2-3]对算法进行了综述:粒子群算法操作简单、收敛能力较强,因此被广泛应用于优化不同领域的优化问题,但是粒子群算法仍有后期多样性差和易于陷入局部最优等不足。因此,近年来粒子群算法的改进与发展受到了许多领域相关学者的关注。粒子群算法的改进策略主要有两类:一种是将粒子群算法与其他算法相结合,构成新的融合算法。文献[4]将差分进化算法与粒子群算法结合起来,在粒子群优化算法中加入了差分变异策略,有效提高了种群的多样性和算法的全局收敛能力。文献[5]将量子粒子群算法和人工蜂群算法相结合识别模型参数,在有噪声数据的处理上,该算法表现良好。文献[6]将人类学习优化算法和粒子群算法相结合,增强了粒子的学习能力,提高了搜索效率。另一种则是对粒子群算法更新策略进行改进,文献[7-9]采用混沌方法对粒子群算法进行了改进,提高了算法的优化能力。文献[10-11]则是通过不同扰动策略提升种群多样性以增强算法性能。文献[12]是通过改变粒子对最优位置的学习策略来提升算法。文献[13-19]在粒子迭代过程中引入新的参数因子,以此调整粒子的更新方式,从而在一定程度上改善算法早熟现象。总体而言,文献[4-19]都是在粒子更新飞行速度和位置时尽可能多地利用当代的信息,但是在此过程中却忽略了对于自身有效历史信息的学习。

除此之外,粒子群算法的研究成果还有很多,但是对于粒子群算法学习自身历史信息的相关研究却很少,使得粒子群在搜索过程中的很多有用信息得不到有效利用。因此,本文提出了一种基于搜索历史信息的粒子群算法(History Information PSO,HIPSO),该算法在原有速度更新公式的基础上,利用学习因子对上代飞行速度进行协同学习,更加充分地挖掘利用粒子群体的当前和历史搜索信息,有效拓展了粒子飞行的路径多样性,很好地提升了算法的搜索能力。

1 粒子群算法

粒子群算法是启发于鸟群协作觅食行为的一种元启发式算法,是一种基于群体协作和信息共享的随机搜索方法。在算法搜索过程中,优化问题的每一个解被看作搜索空间中一个带有速度的粒子,粒子通过速度向量和自身学习能力的强弱来决定它们飞行的方向和距离。因此,粒子速度和位置向量的更新运算是算法生成新解的主要方式。经典粒子群算法具体步骤如下:

第一步,初始化粒子群,包括种群规模N,随机初始位置xi和初始速度vi,其中xi=(xi1,xi2,…,xiD),vi=(vi1,vi2,…,viD),i=1,2,…,N,D表示问题的维数。

第二步,计算每个粒子个体的适应度值,更新个体极值点pi和全局极值点g,其中pi=(pi1,pi2,…,piD),g=(g1,g2,…,gD)。

第三步,根据式(1)和(2)更新每个粒子的速度和位置向量:

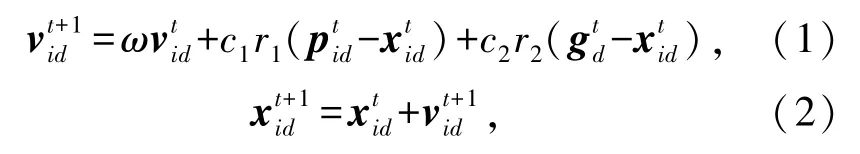
式中:ω为惯性权重;c1、c2是两个正的加速系数,分别为自我学习因子和社会学习因子;r1、r2是分布在 [0,1]内的均匀随机数;表示在第t+1次迭代中第i个粒子在第d维上的速度和位置分量。

2 基于搜索历史信息的粒子群算法

2.1 思想启蒙模型

在市场经济领域中有一个蛛网经济模型,该模型是通过上一阶段的价格来调控下一阶段的产量,即通过上一阶段的经验对下一阶段的决策进行指导[20]。蛛网经济模型的基本假定如下:商品的本期产量Qts取决于前一期的价格Pt-1,商品本期的需求量Qtd取决于本期的价格Pt。蛛网经济模型可用方程组表示:

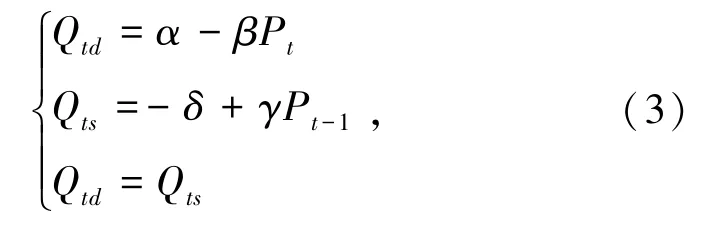
其中,α、β、δ和γ均为常数且大于零[21]。

蛛网模型利用本期产量和需求量建立了前一期价格与本期价格之间的联系,用前一期经验指导本期的相关行为。受此机制启发,本文使粒子群中每个粒子个体的速度除了正常向当代群体的精英粒子学习,还向上一代粒子学习,进而对新个体的搜索进行协同的调整和指导,以此加强粒子群体对历史信息的有效再利用,从而使得粒子的飞行路径更加多样化和差异化,最终提升算法的性能。

2.2 HIPSO算法

HIPSO算法沿用经典PSO算法的架构,对粒子速度历史信息学习的机制通过与当前飞行速度的协作而实现,即在式(1)与式(2)之间加入

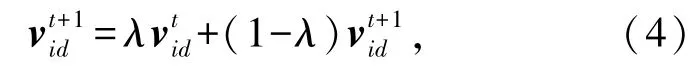
其中,λ为学习因子,用以调整对粒子速度历史信息的利用强度。

本文提出的HIPSO算法共有3种策略:

1)静态学习因子的HIPSO算法。静态学习因子是指算法在迭代过程中,学习因子是一个常数,不随迭代而改变。如图1所示,经典PSO算法中新粒子在三个平行四边形区域A(只向pt-xt方向学习)、区域B(同时向pt-xt与g-xt方向学习)、区域C(只向g-xt方向学习)中由几种启发式信息协同生成,而HIPSO算法生成的新粒子则是在区域D中由几种启发式信息协同生成,搜索区域得到了扩充。

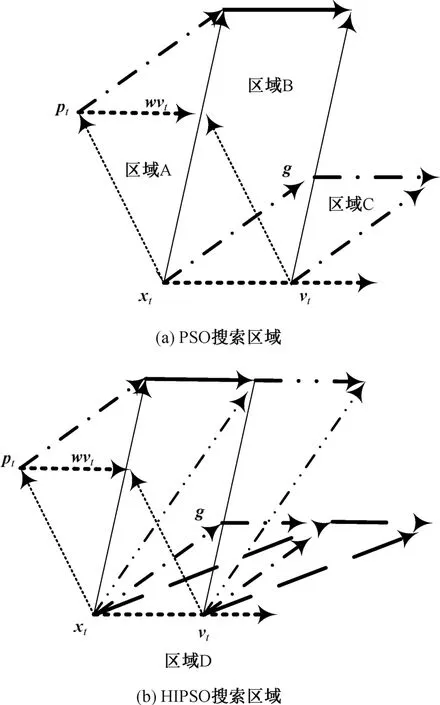
图1 PSO与HIPSO搜索区域区别示意图Fig.1 Thesearch area difference diagram of PSO and HIPSO

通过图1可以看出,通过学习因子的动态调节,可动态调整新粒子可能的飞行方向与原粒子飞行方向之间的跨度,以此扩大粒子的飞行范围,进而增强算法搜索寻优能力。

2)随机学习因子的HIPSO算法。针对静态学习因子参数不易确定的问题,进一步提出随机学习因子HIPSO算法。该算法在每一代的迭代过程中,每一个粒子对应的学习因子在给定因子集合中随机选取。通过学习因子的随机选择,使得粒子的飞行轨迹进一步多样化,增强了种群总体搜索区域的多样性。λ的选取方式为

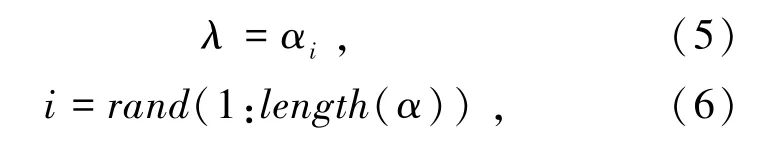
其中,α为学习因子集合,length(α)为集合长度,i为1到length(α)之间的随机整数,αi为集合中第i个学习因子。

3)最优学习因子的HIPSO算法。随机选择学习因子一方面可以多样化飞行轨迹,增强寻优能力;另一方面,随机选择的学习因子会难以避免的使粒子向较差的方向飞行,从而浪费算法的计算资源。因此,需要指导每代种群中每个粒子在因子集合中选取使得上一代中生成新个体最优的学习因子,以此对粒子飞行方向进行指导,尤其是加强精英粒子的经验指导。λ的选取方式为

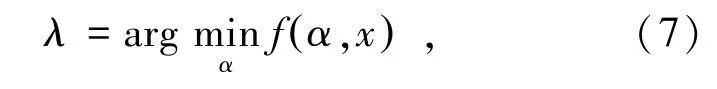
其中,α为学习因子构成的集合,λ是因子集合所有学习因子中对应的使个体适应度值f(x)最优的学习因子。

2.3 越界处理

本文采用的越界处理方式为,若子代个体xnew飞出下界,则xnew取xmax与2xmin-xnew之间的最小值;若子代个体xnew飞出上界,则xnew取xmin与2xmax-xnew之间的最大值,即

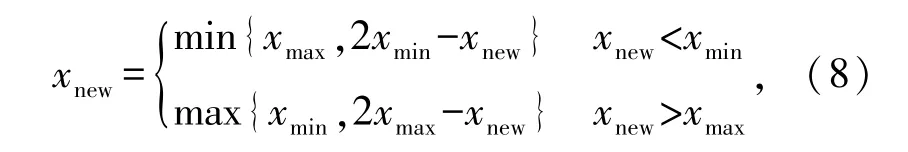
其中,xnew为生成的新个体,xmin为粒子下界,xmax为粒子上界。

2.4 算法流程

算法具体步骤如下:

第一步,初始化粒子群规模N,初始位置xi和初始速度vi。

第二步,计算每个粒子个体的适应度值,并更新个体极值pi和全局极值g。

第三步,选取学习因子。其中静态学习因子策略赋予定值,随机学习因子策略让个体在每次迭代时根据式(5)(6)选取,最优学习因子策略则是根据式(7)选取。

第四步,利用式(1)(2)(4)更新粒子速度和位置。

第五步,进行越界检测,如果越界,通过式(8)进行越界处理。

第六步,判定是否符合终止条件,如果是,输出结果,如果否,返回第二步,重复此循环。

算法整体架构较为简单,静态与随机学习因子策略的加入并没有增加粒子群算法的算法复杂度。而最优学习策略在每次迭代中加入了一次比较排序,该策略的算法复杂度为O(nlogn)。

算法流程图见图2。

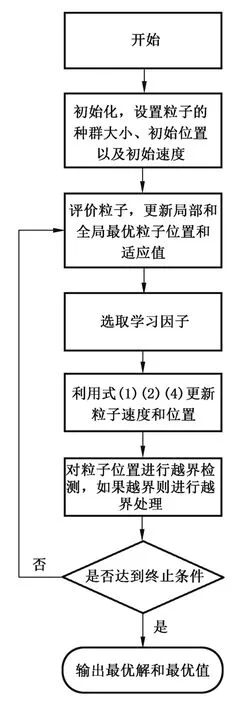
图2 HIPSO的算法流程图Fig.2 Flow chart of HIPSO

3 学习因子的有效性分析

为验证本文所提思想与算法的有效性,用静态学习因子粒子群算法HIPSO(λ分别取0.75、0.5以及0.25),随机学习因子算法HIPSOR、最优学习因子算法HIPSOB与经典PSO算法进行对比分析。

3.1 测试函数与参数设置

在CEC2014函数测试集的各类函数中选取代表性算例构成本文的函数测试集[22],所选函数如下:单峰函数f1、f2、f3,多峰函数f4、f5、f12、f15,混合函数f17、f20,组合函数f23、f26、f28。为方便起见,本文把这些函数重新标记为F1～F12。函数简单信息如表1所示,有关测试函数详细信息请参看文献[22]。

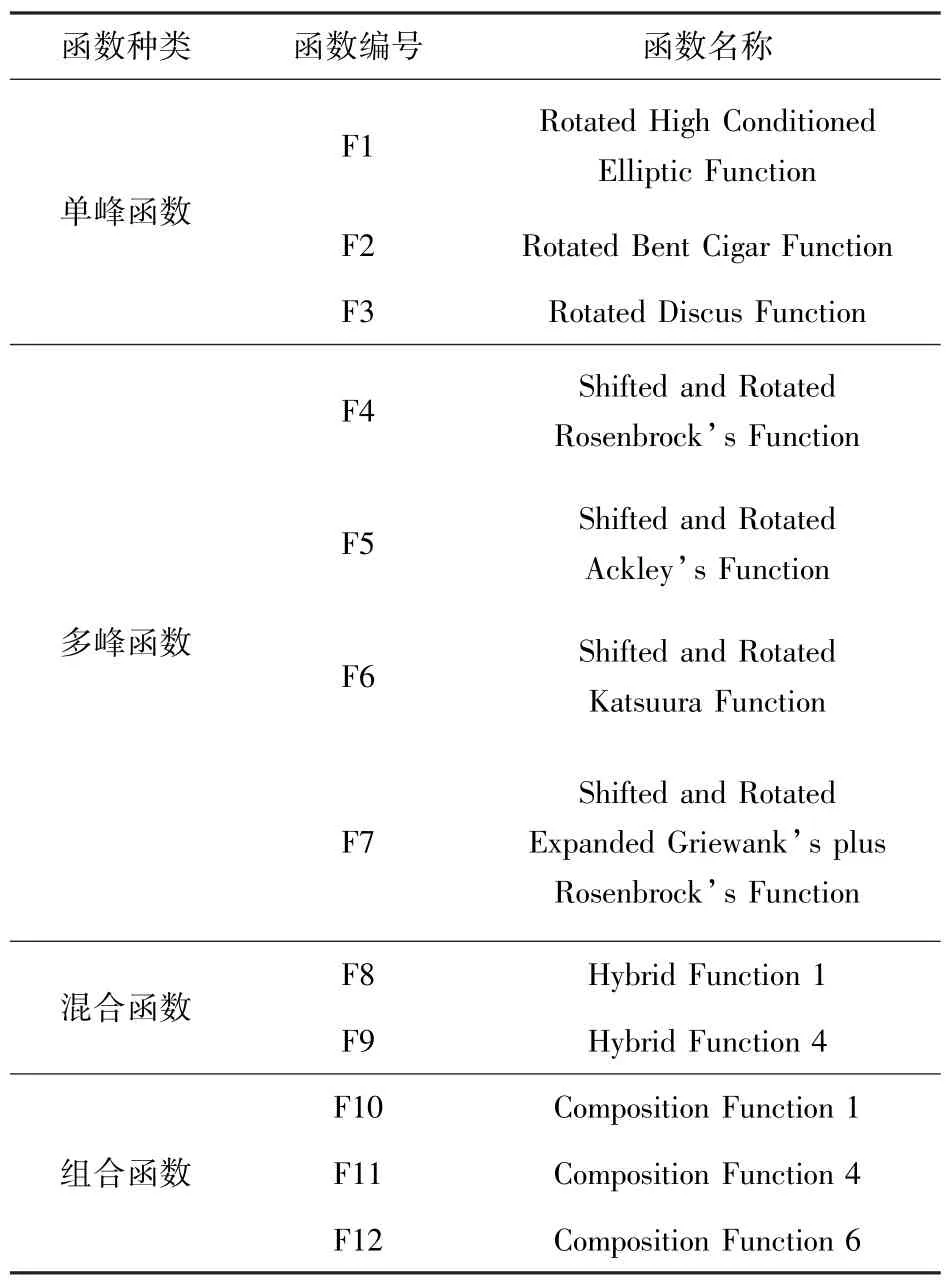
表1 函数测试集Tab.1 Benchmark functions

对比仿真试验的参数设置如下:种群规模N=100,搜索空间维数D=50,惯性权重,加速系数c1=c2=0.5+ln 2,HIPSO的学习因子λ分别为0.75、0.5、0.25,HIPSOR与 HIPSOB的学习因子λ的集合为{0,0.25,0.5,0.75,1-10-6},最大评估次数是10 000D,算法独立运行次数是30。

3.2 数值试验对比

六种算法的数值统计结果如表2所示,统计结果包括30次独立试验最终结果的最优值、平均值和标准差,最优结果用加粗黑体表示。从表2的结果可以看出:

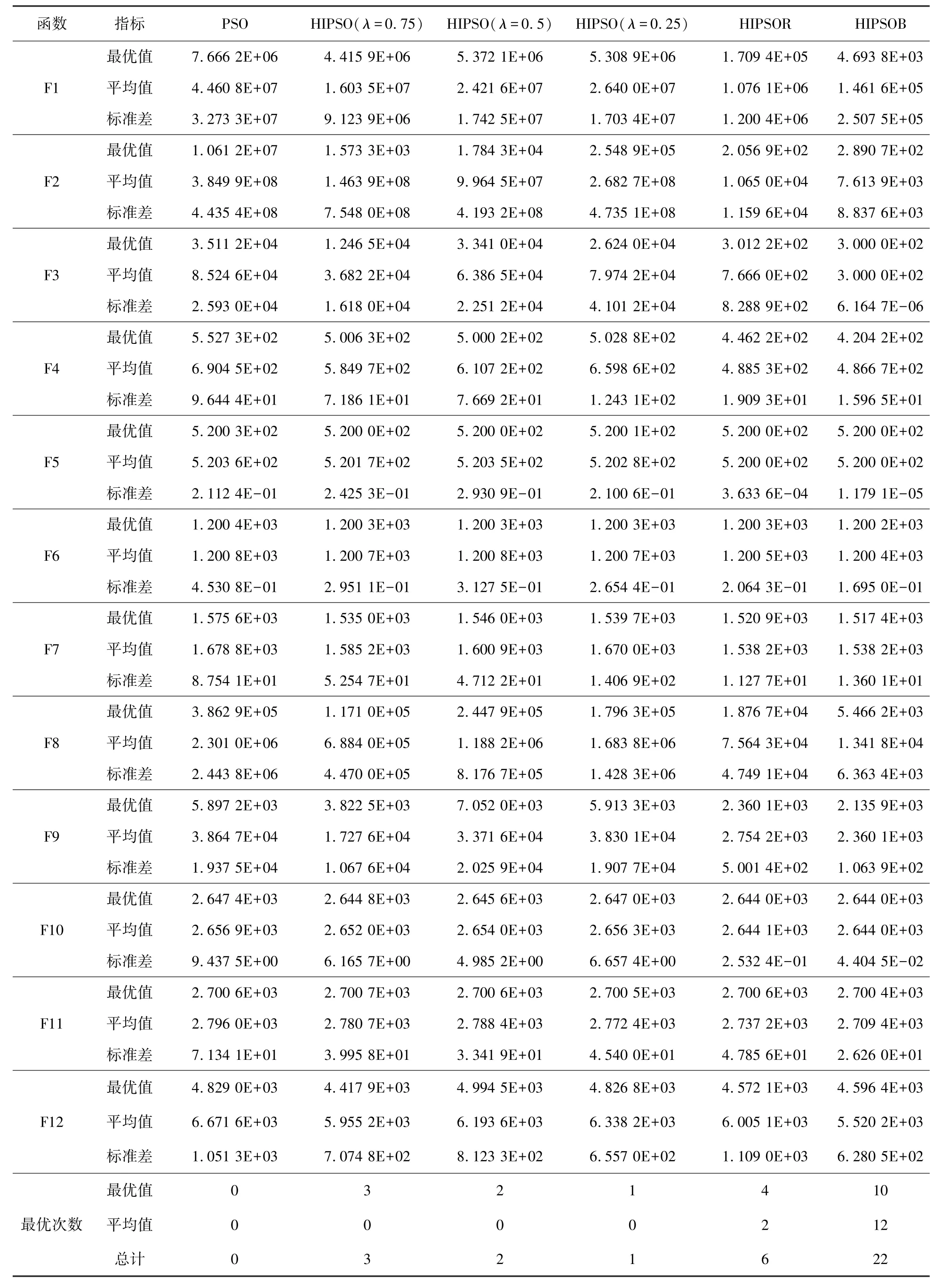
表2 6种算法数值结果统计Tab.2 Experimental results of six algorithms

1)HIPSOB在“最优值”统计项上取得10个最优结果,在“平均值”上统计项全部取得最优结果;HIPSOR在这两个统计项上分别为4个和2个。利用最优学习因子的HIPSOB表现最好,利用随机学习因子的HIPSOR表现次之,利用静态学习因子的三种算法紧随其后,从而说明动态利用历史飞行信息对现有飞行方向进行调整具有很好的效果和较好的潜力。

2)三种静态学习因子粒子群算法HIPSO(λ=0.75)、HIPSO(λ=0.5)、HIPSO(λ=0.25)较经典PSO算法有明显改善,且学习因子越大,对应算法的综合性能越好,从而说明粒子飞行历史信息对粒子群算法的搜索方向改善具有明显的效果。

3)加入学习因子后,对四种类型函数算法均有所改善,在单峰问题上最为明显。需要说明的是,加入学习因子和利用历史飞行信息并没有引入任何有代价的额外运算。

综上所述,HIPSOB算法表现最好,HIPSOR次之,三种静态学习因子均比经典PSO算法的结果更要好,说明粒子飞行历史信息的开发利用对算法性能的改善是有益的,而且动态学习因子策略要比静态学习因子策略更具优势,并且带有启发式指导性的动态选取策略要比随机选取策略效果更显著。

4 与其他经典PSO算法的仿真对比试验

为了进一步分析验证算法性能,将两种动态学习因子的PSO算法HIPSOR、HIPSOB与其他经典PSO算法NmP3PSO[10]和CLPSO[12]进行数值仿真对比试验,以此分析验证与其他更有竞争力同类算法对比时的综合性能。

4.1 测试函数与参数设置

测试函数及维度和HIPSOR、HIPSOB的算法参数与上一组试验相同,而CLPSO、NmP3PSO算法参数设置均与原文相同。

4.2 数值试验对比分析

四种算法的数值统计结果如表3所示,结果包含三十次独立试验最终结果的最优值、平均值、标准差,最优结果用黑体加粗标示。从表3可以看出:

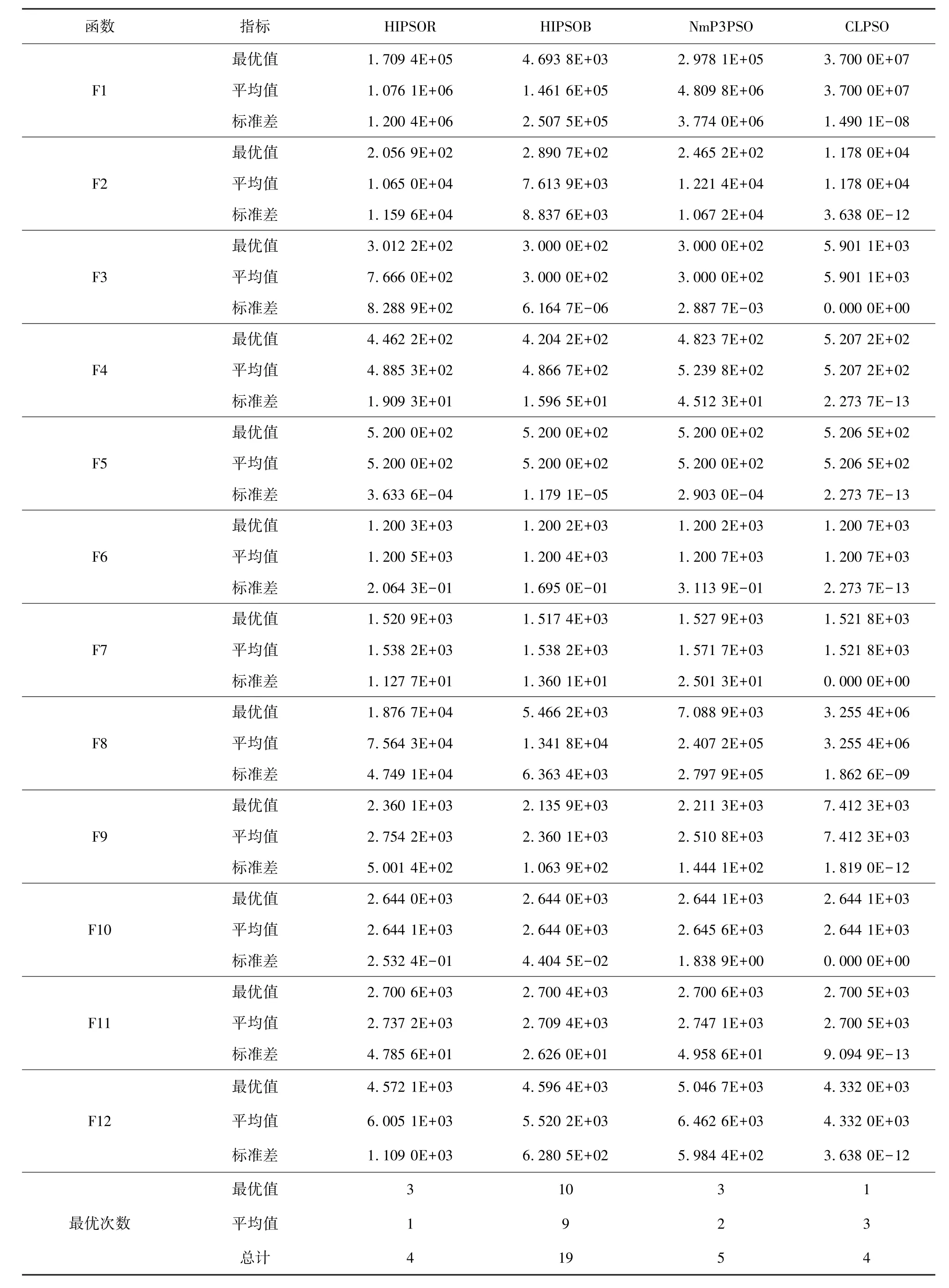
表3 4种算法数值结果统计Tab.3 Experimental results of four algorithms

1)在“最优值”和“平均值”统计项上,HIPSOB表现最优,分别取得了10个和9个最优结果。

2)在单峰、多峰和混合函数上HIPSOB综合表现最优,但是在组合函数上CLPSO表现较为稳定,原因可能是CLPSO综合的学习方式可以获得更多优秀粒子个体有益的飞行信息。

综合表3数据结果以及对比分析情况综合可知HIPSOB算法具有最好的性能。

4.3 算法进化趋势对比

为了考查四种算法的动态平均进化趋势,本文选取单峰函数F1、多峰函数F6、混合函数F8以及组合函数F11进行在线性能对比分析,对比结果如图3所示。

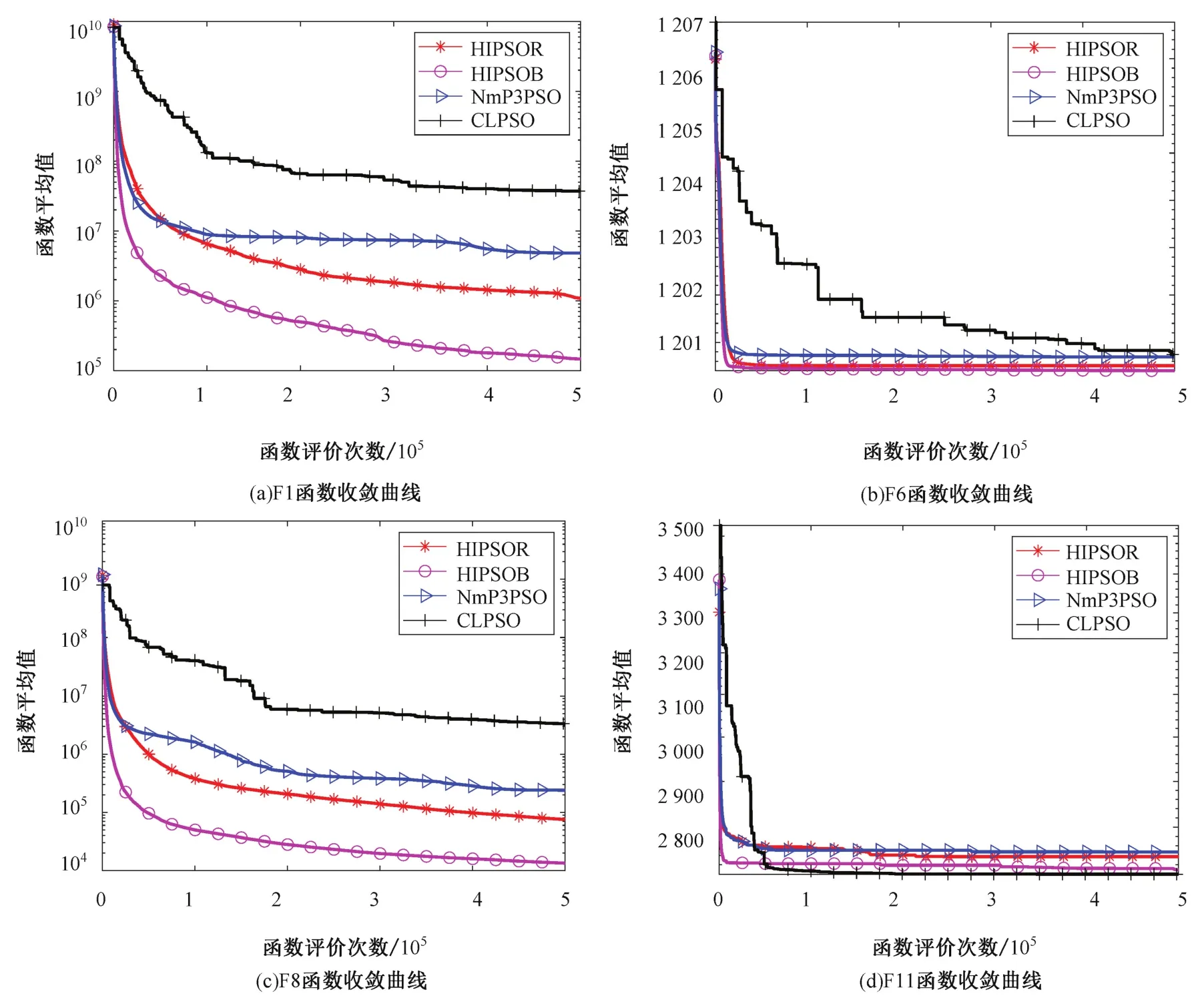
图3 算法收敛趋势对比图Fig.3 Evolutionary comparison of convergence trends

通过图3收敛曲线趋势可以看出:对单峰函数F1,HIPSOB算法不仅收敛速度最快,而且收敛精度明显高于其他算法,HIPSOR也取得了不错的结果;对于多峰函数F6,HIPSOB算法收敛速度依旧是最快,收敛精度略高于其他算法;对于混合函数F8,HIPSOB算法收敛速度最快,并且收敛精度较其他算法高出了2～4个数量级,HIPSOR仅次于HIPSOB;对于组合函数F11,HIPSOB算法的收敛速度最快,但是陷入了局部陷阱,在收敛精度上略逊于CLPSO。总体而言,在四类函数中,本文提出的HIPSOB的收敛速度均为最快,而收敛精度综合表现最好,因此在算法整体收敛趋势统计对比试验中,HIPSOB的综合表现最佳,从而进一步说明本文提出的基于粒子飞行历史信息再利用机制的有效性。

5 结论

为了充分利用群体飞行的历史速度信息,在经典PSO算法的基础上,本文引入了一种对历史速度信息的学习机制,从而提出基于搜索历史速度信息的粒子群算法:静态学习因子HIPSO算法和动态学习因子HIPSO算法(HIPSOR、HIPSOB)。HIPSO算法通过该学习机制,在一定程度上改善了算法的早熟现象,静态选取计算量小,但同时也限制了搜索方向。因此,在此基础上提出了HIPSOR、HIPSOB,进一步提升了算法性能。以CEC2014测试函数集进行数值仿真对比试验,验证了粒子飞行速度信息再利用机制是有效的;然后,将 HIPSOR、HIPSOB与经典 PSO算法变种NmP3PSO、CLPSO进行数值对比试验与进化趋势对比分析,结果表明本文所提出的最优学习因子算法HIPSOB的收敛速度与收敛精度的综合表现性能最佳。