海冰对海浪影响研究综述

管长龙，李静凯，刘庆翔

（1.中国海洋大学 海洋与大气学院，山东 青岛 266100；2.中国海洋大学 物理海洋教育部重点实验室，山东 青岛 266100）

全球气候变化是当今人类社会面临的重大环境问题。气候变化的影响在南北两极海冰的变化上也得以充分体现，尤其在北极海域，伴随着“北极放大”的升温现象[1]，近年来海冰迅速减少，为海浪成长提供了更加充分的风区条件，使得北极夏、秋季海浪不断增强，进而引发了愈加显著的海浪-海冰相互作用。

早在20 世纪30 年代，学者们就已经开始了波浪-海冰相互作用实验研究，至20 世纪中叶已发展出许多数学物理模型，并在70 和80 年代开展了较大规模的海冰边缘区的现场观测工作[2-3]。但是，在当前气候变化的背景下，人们渴望更加充分地认识并能够预测海洋环境变化，世界各国对北极空间与资源利用也有了新的需求，促使海浪与海冰相互作用的研究受到了国际物理海洋学界前所未有的关注。伴随着海洋观测与模拟技术的不断提高，海浪与海冰相互作用方面的研究在近30 年取得了迅速的发展与长足的进步。

当海浪在存在海冰的海域传播时，必然会受到海冰的影响，导致能量的衰减与散射，引起传播速度的变化乃至发生折射。另一方面，海浪本身也会通过多种物理过程引起海冰的破碎、漂移、碰撞和堆积，浪致混合等动力过程也会间接对海冰的热力过程产生影响。本文仅从物理海洋学的角度出发，针对海冰对海浪作用有关的国内外研究现状进行介绍和总结。

海冰对海浪的作用可以分为间接与直接两个层面。间接作用可以理解为海冰对海浪风区的影响[4-5]，即海冰通过改变更大尺度上无冰开阔海域的形状影响所关注海域海浪的成长与演化。目前常用的处理方法是将（100%-海冰密集度）作为比例系数乘以常规的风与浪之间的作用，也就是当海冰密集度为100%时，就忽略海面风场对海浪的能量输入。与之相比，海冰对海浪的直接作用则是学者们研究的重点，主要归纳为海浪能量的耗散和海浪传播速度（频散关系）的改变两个方面。

1 海冰对海浪能量的耗散

海冰对海浪能量的耗散是海冰对海浪作用研究的核心问题，也是海冰-海浪相互作用研究的基础问题。长期以来，各国学者利用多种研究形式与手段，给出了多种量化该物理过程的方法。最早在20 世纪60 年代，研究人员就通过船载测波仪观测发现海冰边缘区海浪能量E随传播距离x的增加呈现指数衰减[6-7]，即：

式中：α为能量的衰减系数。之后，一系列不同形式的观测结果[2,8-9]也都证实了冰下海浪的传播符合这一规律。直到2014 年，Kohout 等[10]在Nature上发表了2012 年南极海冰边缘区海浪的观测结果指出，当海浪的有效波高Hs超过3 m 时，=-16.05×10-6，这也意味着海浪能量随传播距离的增加呈现线性衰减。不过，后续的一些研究表明：该现象依然可以通过经典的指数衰减理论进行解释，衰减系数α随频率的变化[11]以及局地的风能输入和波-波非线性相互作用[12]可能会影响所观测到的冰区海浪衰减特征。Kohout 等[13]于2020 年进一步分析发现2014 年的结论主要是由数据量过少等原因造成的。

基于上述经典的能量指数衰减规律，海冰对海浪能量耗散的研究重点即可转变为对能量衰减系数的研究。海浪能量的衰减源于表面波与浮冰之间的相互作用，所以该衰减系数一定与海浪以及海冰本身的物理性质密切相关，而复杂、多样的海浪与海冰属性又进一步决定了衰减系数的确定或者是给出通用的计算形式是较为困难的研究工作。

1.1 海冰-波浪理论模型

从海浪能量的耗散方式来看，可以分为海冰对海浪直接的非线性作用和浮冰边缘对入射海浪的散射两种主要形式。前者会直接衰减波动的能量，后者虽不会衰减能量，但是会减小海浪传播方向上的能量。通常在海冰密集度较小的海域，尤其当浮冰尺寸与海浪波长相当时，散射效应的影响会相对更大[14]，在实际的研究中也常常同时考虑2 种作用机制[15]。

考虑海面上浮冰数量的不同，研究者们分别构建了针对单个或多个浮冰的海冰-波浪理论模型。针对单个浮冰，Montiel 等[16-17]曾利用波浪水池的实验验证了海浪与漂浮弹性圆盘（类海冰材料）作用的一个线性模型；Bennetts 和Williams[18]提出的模型则更为复杂，可以适应任意光滑的海冰形状。这类模型尽管可以有效地计算出海浪能量的散射和透射，但是现实的海冰边缘区浮冰数量巨大，逐一对每一个海冰进行计算是不切实际的。所以，针对多个浮冰的理论模型相对而言更适合海冰边缘区海浪能量散射的模拟。常见的思路是将海冰假设为许多平行的二维冰板，进而计算波动在浮冰之间多次的反射与透射[18-22]，虽然计算过程十分复杂，但是，在应用中可以结合实际的波动周期和海冰厚度等参量直接参考前人理论模型的计算结果[21]（见图1）来获得能量衰减系数。为了更接近于实际海洋中多样的冰情，后续也有一些研究考虑不同海冰形状等其他变化的影响，但这也会使得计算更加复杂。

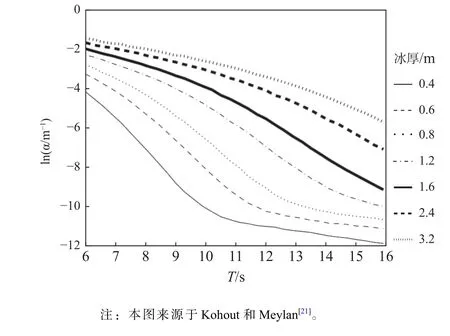
图1 模拟的衰减系数α（取自然对数 ln(α)）在不同冰厚条件下随波动周期T 的变化Fig.1 Predictions of the logarithm of the attenuation coefficient with variations in wave period and ice thickness

在实际的极地海洋中，大面积在空间上近似连续的海冰覆盖于海面之上是十分常见的情形，沿岸冰也是类似的情况。这使得通过将海冰视为海面之上的连续介质来构建海冰-波浪模型在物理意义上具备一定合理性。连续介质理论通常会忽略海冰-海冰、海冰-海水间具体的实际物理过程，考虑两层体系，均一且有限厚度的冰层覆盖在水层之上，通过建立连续体本构模型来计算海冰对海浪能量的衰减。根据连续介质（冰层）的不同物理属性，可以延伸出不同的理论模型。Wadhams 等[3]和Wadhams[23]将连续的冰盖看作弹性材料，并假定海冰的厚度相对于海浪的波长是小量，然后将弹性薄板的弯曲理论应用于冰盖，基于欧拉-伯努利梁方程发展成薄弹性层模型。Fox 和Squire[24]与Squire[25]后续对该类模型又进行了完善与发展。Liu 和 Mollo-Christensen[26]与Liu 等[27]在薄弹性层理论的基础之上考虑了冰盖下表面的粗糙度，认为在这个非平面附近的水体运动将会引起湍流，然后把这个过程以涡流黏度的形式来体现。基于实验室观察到的波浪在油脂冰下的传播，Keller[28]提出把海冰看作一个纯黏性层，而海水被视为无黏的，提出了最早的黏性层模型。De Carolis 和Desiderio[29]考虑了海水的黏性，又对该模型进行了拓展。De Santi 等[30]将黏性层模型模拟的衰减系数与部分极地现场观测数据进行了对比，发现二者吻合较好。若同时考虑海冰层的弹性与黏性，则可发展成为黏弹性海冰-波浪模型，Wang 和Shen[31]基于Voigt 本构方程提出的模型便是其中最具代表性的模型之一，也是最早植入第三代海浪模式WAVEWATCH Ⅲ的黏弹性模型，该模型的优势之一是可以在一定理想条件下分别简化成为质量荷载模型[32-33]、薄弹性层模型和黏性层模型。Zhao 和Shen[34]进一步考虑了冰下湍流边界层的涡流黏度，进而将该黏弹性模型发展成一个3 层模型。针对目前较为常用的3 个黏弹性模型，Mosig 等[35]较为详尽地分析和对比了它们的特点。

目前，绝大部分的海冰-波浪模型对海浪的处理依然基于线性波动理论，波动的基本形式表达为Aei(kx±ωt)，其中：A为波动的振幅；x为波动的传播距离；t为时间；k为复波数且k=kr+iki，实部kr为通常意义的波数，虚部ki为海冰引起的能量衰减。需要说明的是，此处讨论的是波动振幅A的衰减，因为波动的能量密度与振幅的平方成正比，所以对应的振幅衰减系数ki应 为能量衰减系数α的一半。

经过几十年的研究，人们已经发展出了许多海冰-波浪模型，但受篇幅所限，本文仅提及了部分较为代表性的模型。不过，尽管模型众多，却不存在某个模型可以适用于各种海冰类型的情况。因为在实际海洋中，海冰种类繁多，形态复杂多样，包括碎冰、尼罗冰、油脂冰、莲叶冰以及大面积连续的冰盖等，所以构建一种普适性很强的海冰-波浪模型目前还无法实现。黏弹性海冰-波浪模型尽管可以通过调整海冰的弹性与黏性以适应多种海冰类型，但在实际应用中也依然存在一定的局限性。除了模型本身理想的理论假设与实际情况存在偏差之外，部分模型较为复杂，无法获得解析解，以Wang 和Shen[31]黏弹性模型为例，常用的数值求解的方法（包含无穷个数值解）难以保证获得最具物理意义的特征根。此外，还有一个普遍性的问题，就是海冰物理属性参数难以准确确定。模型中常用的海冰的弹性、黏性等参数与材料力学中对应的数值是不同的，而且即便是同一物理参数在不同的海冰-波浪模型中，数值也会有所不同，所以通常称之为各模型的等效参数，如：等效剪切模量和等效运动黏度系数等。因此，明确各种海冰的等效参数是各海冰-波浪模型得以开展实际应用的前提。通过实测海冰覆盖海域特定海冰类型下海浪的衰减参数反算或者校正各模型中的海冰属性参数是当前最普遍的方法[11,36-38]。

1.2 冰区海浪观测数据分析

除了从理论模型的角度来量化海冰对海浪的能量耗散之外，另一种更加直观的思路是通过海冰覆盖海域海浪衰减系数现场观测数据的拟合等数据分析方法来获得经验关系式。随着近几年极地海域海浪现场观测数据的逐渐增多，这种方法的可行性也在不断增加，虽然背后的物理意义相对薄弱，但是其简单且高效。Meylan 等[39]利用南极海冰边缘区的海浪观测数据给出了能量衰减系数α（单位：m-1）与周期T的关系，即：

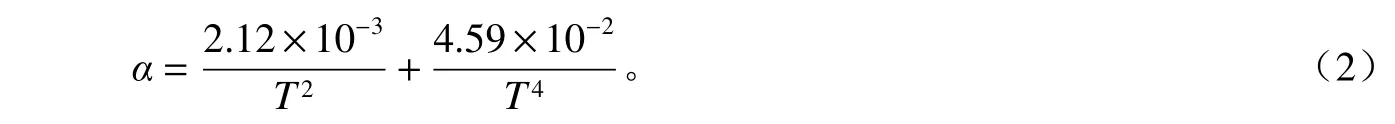
Doble 等[40]利用威德尔海莲叶冰区为期12 d 的观测数据拟合出了2 个关系式：

式中：T为波动周期（单位为s）；h为海冰厚度（单位为m）。Rogers 等[41]利用波弗特海的多组观测数据，借助阶梯函数给出了多个能量衰减系数α与周期T的拟合关系式。

综合目前南北两极海冰边缘区的多组海浪观测数据，可以发现绝大多数观测到的海浪能量衰减与波动频率均可利用幂指数关系进行拟合，且幂次多为2～4。Meylan 等[42]在此基础上进一步结合多组海冰-波浪模型的理论解，给出了多组振幅衰减系数ki与 频率 ω的 幂指数关系式，例如：（η为等效黏度系数，ρ为海水密度，g为重力加速度），该式被Liu 等[43]应用于波弗特海冰边缘区海浪的数值追算，并取得了较为理想的模拟精度。

总体来看，海浪的能量衰减系数α与波动频率的n次幂成正比[42]（见图2），即α(ω)∝ωn（n＞1），这是符合当下研究者基本认识的，表明海冰对频率更高的波动衰减更强。这一结论与迄今为止绝大多数观测和理论结果[14]是一致的，但是也有特例，即所谓的表面波衰减系数的“rollover”现象。“rollover”现象指的是海浪的能量衰减率在某一频率达到最大值，然后随频率的增加而减小的现象。目前该现象只在海浪现场观测数据中发现过[40,45-46]，且绝大部分的理论模型都无法模拟出该现象。Li 等[46]通过数值模拟的分析认为该现象可能是由于局地风能输入及四波非线性相互作用对在有冰覆盖海域传播的表面波的作用。Thomson 等[47]于2021 年研究发现，仪器的观测误差也可能会导致在计算海浪衰减率时发生“rollover”现象。

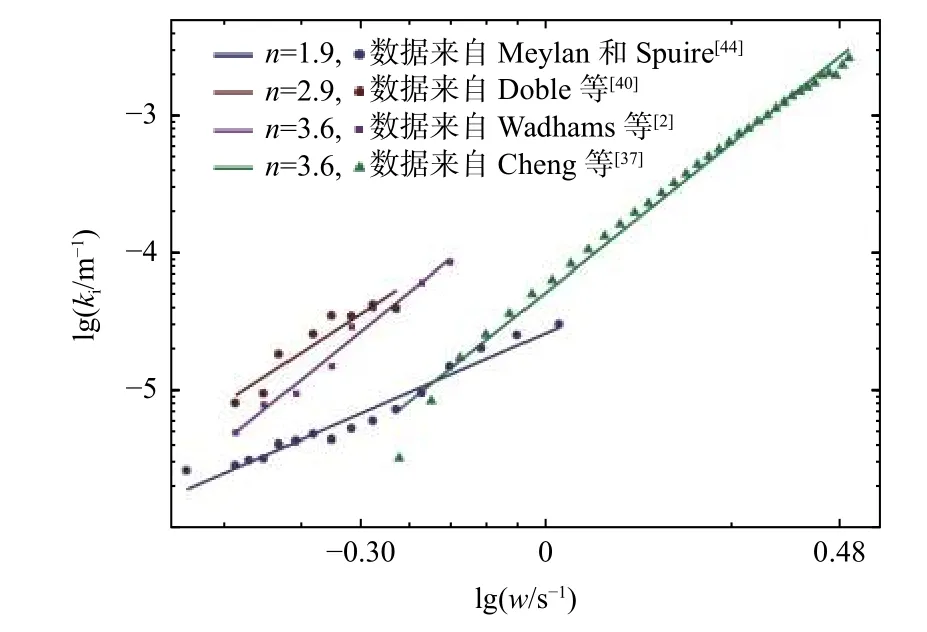
图2 多组海冰覆盖海域实测的波数虚部（ ki）的中值随波动圆频率 ω=2πf的变化Fig.2 Median values of imaginary wave number components(ki)versus angular frequencyω=2πf

2 海冰对海浪频散关系的改变

海浪作为一种小尺度运动，其频散关系 ω=ω(k)具有普适性，但是，当海表面被海冰覆盖时，无冰开阔水域的波动频散关系是否依然适用成为研究者关心的另一个问题。

从数理模型的角度来讲，通常认为波动的频散关系会因海冰的存在而发生改变，因为波动的表面不再自由，而是会受到冰盖弯曲（形变）的影响[14]。如果将海冰看作弹性、黏性或者是黏弹性，亦或是不同厚度、不同形状等，那么当海浪存在时，其弯曲的表现一定不同，也就是说，海冰类型不同时，海浪频散关系的修正方式也会不同。Zhao 等[48]和Meylan 等[42]总结了基于多种海冰-波浪模型的具体波动频散关系，本文在此不再赘述。由海冰-波浪理论模型（1.1 节所述）可知，在绝大多数的海冰-波浪模型中，波数是以复波数k=kr+iki形式体现的。那么，对各海冰-波浪模型（尤其是连续介质模型）所提出的波动频散关系进行求解，便可获得kr和ki，前者可以量化波动传播速度的改变，后者代表波动能量的衰减。

从观测的角度来讲，学者们利用多种观测形式研究了海冰对海浪频散关系的影响。Newyear 和Martin[49-50]在实验室对油脂冰情况下单频波传播过程中频散关系的变化进行了测量与分析。Sakai 和Hanai[51]利用聚乙烯板代替海冰开展了水槽实验，并基于实验观测数据提出了一个经验性的波动频散关系式。利用南极海冰边缘区浮冰的移动，Fox 和Haskell[52]对波动频散关系进行了估算，发现k∝ω2.41，这一结论显著偏离了无冰开阔水域中k∝ω2的关系。Cheng 等[37]对2015 年秋季在波弗特海莲叶冰为主的海冰边缘区观测到的海浪的波数与无冰开阔水域的波数进行了初步对比，结果（见图3）表明观测到的波数较经典波动频散关系计算的波数偏大或偏小的情况均有发生。Collins 等[53]对该次观测数据做了进一步的分析发现，当波动频率为0.1～0.3 Hz 时，频散关系和无冰水域时基本一样，但是当波动频率大于0.3 Hz 时，观测到的波数较无冰水域略大。

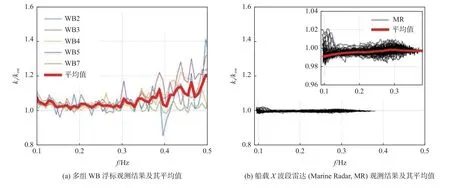
图3 观测的实波数（ kr）与 无冰开阔水域波数（ kow）之比随波动频率f 的变化Fig.3 Ratio of the real wavenumber ( kr) over open water wave number ( kow) with variations in wave frequency

3 考虑海冰作用的海浪数值模拟

无论是关注海冰对海浪能量衰减还是对传播速度变化的影响，其重要目的都是希望提升海冰覆盖海域（尤其是极地海域）海浪数值模拟乃至预报的能力，这也是充分认识环境变化、合理开发利用极地资源的重要前提。

在当前主流的第三代海浪模式中，深水条件下波作用量方程（忽略海流作用）可以写成如下形式：

式中：N为波作用量，能谱密度与圆频率的比值；t为 时间；ω为 波动频率；cg为 群速度矢量；S为各种物理机制所对应的源项之和，考虑海冰的作用后，其可以写成：

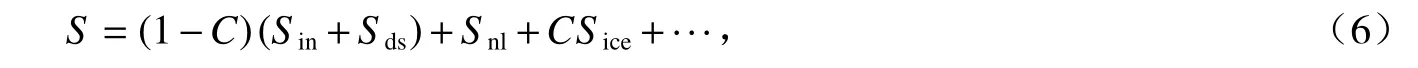
其中：C为海冰密集度；Sin为风能输入项，Sds为破碎耗散项，二者只在无冰覆盖的水域（100%-C）发生作用；Snl为 四波非线性相互作用项，通常与无冰水域的计算方式相同；Sice为海冰作用项，只在海冰覆盖时发生作用。根据实际的研究需要，S还可以包括三波非线性相互作用、海底摩擦等其他物理机制。

因此，在实际的海浪数值模拟中，不同理论、不同形式的海冰对海浪能量耗散的计算对应的即为Sice中不同的参数化方案。作为首个引入Sice，也是目前Sice可选参数化方案最多的第三代海浪模式WAVEWATCHⅢ，在2019 年发布的最新版本（v6.07）中包括了恒定的能量衰减系数、涡流黏度模型、黏弹性模型、波动频率相关的经验公式和散射模型多种参数化方案的选择[54]。针对特定海冰类型影响下的海浪模拟，利用相应的参数化方案，通过海冰-波浪模型的参数调节，可使海浪参数的模拟达到不错的精度。目前许多的追算实例已经在海浪参数的模拟中实现了精度较好的应用[11-12,15,36,46,55]。另一个主流的第三代海浪模式SWAN 也于2019 年底发布了41.31 版本，其中加入了基于波动频率的多项式来计算海冰对于海浪能量的耗散[56]。

对于大多数的冰区海浪数值计算而言，虽然目前学者们只在Sice项中考虑了海冰对海浪能量的耗散作用，但是如果选择像Wang 和Shen[31]提出的黏弹性模型的方案（IC3），WAVEWATCH 是有能力在计算中考虑海冰对海浪波数kr的影响的。此外，在实际海洋中，海冰一定不是单方面地只对海浪产生影响，二者之间一定是同时进行着相互作用。海浪通过动力作用可以使海冰破碎、碰撞和堆积等[25]，而海冰形态的变化进而又会使其对海浪能量的衰减能力产生改变。WAVEWATCH Ⅲ v6.07 版本中Sice的IS2 方案在计算过程中便考虑了由海冰破碎引起的海冰直径的变化，并将这种变化体现在海浪能量散射和耗散的计算中。

4 海冰影响下的海浪现场观测

为了更加充分、准确地认识海冰对海浪的影响，对理论模型和参数化方案进行有效地完善与参数订正，长期以来学者们开展了不少的现场观测研究。Squire 和Moore[9]早在1980 年就利用安装在浮冰顶部的加速度计测量了海冰各个方向的起伏，结合海冰外缘波浪骑士的观测数据证实了海浪能量在冰区呈指数衰减且波动频率越高衰减越强的结论。Wadhams 等[2-3]通过综合分析东格陵兰海、白令海和弗拉姆海峡海冰边缘区的一系列海浪观测数据，首次发现了表面波衰减系数的“rollover”现象，并且发现海冰覆盖海域外缘的碎冰区对海浪具有显著的散射效应。

近年来，随着人们对极区环境变化关注度的提升以及观测技术的不断发展，冰区海浪的观测活动愈加频繁。Frankenstein 等[8]利用2 组嵌在密集度较高的碎冰区的倾斜仪加速度计验证了波动能量的指数衰减率，并且发现高密集度的碎冰较直径更大的离散海冰对海浪的衰减更强。挪威科技大学和斯瓦尔巴大学于2016年的一项联合考察项目中也通过在巴伦支海海冰边缘区的浮冰上固定多个惯性测量单元（IMU）来测量冰区海浪的传播，2020 年，Liu 等[43]利用该组数据对WAVEWATCH Ⅲ模式的相关源项进行了检验对比。在北冰洋海冰边缘区的诸多海浪观测中，最系统、最具代表性的观测无疑是2015 年秋季在波弗特海海冰边缘区的现场观测，2018 年，Thomson 等[57]较为详尽地介绍了此次 “Arctic Sea State Program”，此次观测由美国和加拿大等国家的多所院校和科研机构共同合作完成，在R/V Sikuliaq 号为期42 天的航行期间布放了6 个SWITF[58]、10 个WB[40]和1 个NIWA[59]浮标，获得了大量、详尽的以莲叶冰为主的海冰覆盖海域的海浪观测数据。这些观测数据在后续很多工作中都得到了进一步有效的利用[11,60]，极大地推动了人们对北极海冰边缘区海浪的认识以及相关数值模型的校准。Rogers 等[36]和Cheng 等[37]基于黏弹性海冰-波浪模型的分析认为对于以莲叶冰为主的海域，海冰的黏性效应占据主导作用。图4 为上述提到的波弗特海与巴伦支海两次海冰边缘区海浪观测期间的现场照片[53]。

图4 北极海冰边缘区海浪传播的现场照片Fig.4 Photos of wave propagation in marginal ice zones of the Arctic Ocean

在南极的海冰边缘区，学者们同样开展了具有重要科学意义的海浪现场观测试验。例如：2012 年9 月至10 月，Kohout 等[59]在SIPEX-2 项目期间布放了5 个漂流式浮标，获得了连续长达十几天的冰区海浪观测数据。这些数据对冰区表面波衰减的研究[10-12,39,42,46]十分有益。此后，Kohout 等[13]于2017 年在罗斯海PIPERS 项目期间再次开展了南极的海冰边缘区的2 组海浪实地观测，共计投放了14 个浮标，浮标存续时间最长可达6 周。Doble 等[61]于2000 年4 月在南极威德尔海的海冰边缘区也开展了基于STiMPI 项目的海浪观测活动，共布放了6 个WB 浮标，工作时间最长的1 个浮标一直持续到当年10 月，关于此次观测的详细介绍以及相应的数据分析研究参见文献[15,40,61-62]。除了上述提到的现场观测之外，其实还有一些不同形式、不同地点的现场观测，针对沿岸冰、碎冰和油脂冰等多种海冰类型[63-66]，帮助人们进一步认识了不同类型的海冰是如何影响海浪传播的。

基于浮标等设备的现场观测固然能提供高质量且相对准确的数据，但其在时空覆盖范围上存在明显不足，对海冰与海浪随时空变化的观测能力有限。相比之下，卫星遥感和飞机搭载的传感器可以提供海冰边缘区更大范围的海浪观测数据。所以早在20 a 前，学者们就已经开始研究通过合成孔径雷达（Synthetic Aperture Radar，SAR）数据反演海冰覆盖海域的频散关系等海浪信息[67-70]。近些年，利用卫星搭载的SAR 数据，Ardhuin 等[71-74]通过改进基于Sentinel-1A 波模式图像的算法先后反演了南北两极海冰覆盖海域涌浪的波高和海浪谱，估计了海浪能量的衰减，并与现场观测结果吻合较好。Stopa 等[75]同样利用Sentinel-1A 的SAR 图像数据计算了波弗特海海冰覆盖海域400 km × 1 100 km 范围内的海浪衰减，发现高频波动可以被海冰快速衰减掉，并且冰间水道的存在会影响海浪谱的反演。Shen 等[76]利用RadarSat-2 的SAR 数据反演了格陵兰岛东南部海冰边缘区海浪能量的衰减与频散关系。Sutherland 等[77]利用机载扫描雷达观测了海冰外缘线附近的200 多组数据并计算分析了海浪方向谱的特征。

5 结论与展望

经过学者们长期的努力，海浪在海冰覆盖海域传播的研究已经有了较好的理论框架和一定的应用基础，并通过多元化的观测不断加深人们的认识，推动着该方向研究的持续发展。总的来说，在海冰覆盖海域，海浪的能量随传播距离增加呈指数衰减且衰减系数与波动频率的幂指数相关已是人们达成的共识。另外，海冰的存在同样会一定程度上改变海浪的频散关系，而改变的程度会受海冰本身物理属性的影响。不过，也需要意识到当前关于海冰对海浪作用物理机制的认识还是有明显欠缺的（例如，对于在海冰边缘区十分常见的莲叶冰而言，其衰减海浪能量的具体物理过程是怎样的），这都需要在未来的研究中不断地完善。关于早期海浪与海冰相互作用详尽的研究综述可以参见Squire 等[78]和Squire[25]，近年来该方向的研究发展综述可以参见Squire[14,79]。

全球气候变化使得极地海冰经历着明显的变化，尤其在北极海域，夏季海冰呈现显著减少趋势，一个可航行水域越来越开阔的北冰洋为未来北极经济和军事活动的开展以及资源的开发与利用提供了前所未有的机遇，同时也对北极海浪的研究提出了新的要求。区别于无冰开阔水域，海冰对海浪的作用是认识北极海浪变化规律以及进行海浪预报的核心问题。尽管前人的研究已经取得了大量的成果，但是从实际应用的角度出发，亟须解决的科学问题至少包括以下3 个方面。

1）在当前几乎所有的海浪模拟中，海冰密集度都以线性的形式来比例化相应的源项，并且风-浪之间、波-波之间的相互作用基本沿用以往无冰的计算方法，这种近似的准确性依然存疑、值得探讨。

2）绝大部分海冰-波浪模型中的参数尚未有系统的确定方法，只能通过针对某种冰情的少数观测数据反演推算。

3）海冰和海浪相互作用的物理本质是耦合问题，倘若从耦合的角度开展计算，目前采用的参数化方案是否需要进一步完善，耦合模式的计算精度与独立计算的海浪模式相比是否具有优势?

上述3 个方面问题的解决依然需要开展许多理论和数值模拟的研究，并且需要更多不同海冰类型下、较大时空范围内海浪的实测数据来进行模型检验、参数校准与规律分析，这样才有可能在未来实现北极海浪大范围、高精度的模拟和预报。同时，准确量化冰区海浪的传播与演化也将为海浪对海冰作用的研究打下坚实的基础。