基于改进BIT算法的农业机器人路径优化研究

陆宇豪1，刘义亭2,3，郁汉琪4，余 伟5

（1.南京工程学院 研究生院，南京 211167；2.南京工程学院 自动化学院，南京 211167；3.东南大学 信息科学与工程学院，南京 210096；4.南京工程学院 工业中心，南京 211167；5.华龄和平南京智能科技有限公司，南京 210000）

0 引言

路径规划技术作为农业机器人领域的重要技术，其目的在于寻找源与目标之间的最佳路径，并要求路径安全无碰撞、算法收敛速度快[1]。目前，路径规划算法种类较多，主要有基于图搜索的A星（A-star）算法和基于采样的快速搜索随机树（Rapidly Exploring Random Trees，RRT）算法。

其中，以A星为代表的基于图搜索的路径规划算法主要是通过设定合适的启发函数指导栅格点的搜索，从而获取最优路径[2]。此类算法在小地图环境下响应极快，且生成路径最短。但在农业大场景下，A星算法的计算量会迅速上升，搜索效率降低，且实时性差。

以RRT为代表的基于采样的路径规划算法主要通过对空间点进行随机采样，将初始点作为随机树的根节点，在约束条件下扩展随机树并最终形成一条连通路径[3]。此类方法无需对地图进行预处理，适用于大型平面或高维空间的路径搜索，搜索速度较快，但在没有适当采样指导的情况下搜索较为盲目，性能不稳定且耗时较长，获取的路径也并非最优[4]。

针对上述A星算法与RRT算法的优缺点，Jonathan D. Gammell提出了一种将图搜索和随机采样思想相结合的批量通知树（Batch Informed Trees，BIT）算法[5]。该算法能够在获得移动成本最优路径的同时避免大空间环境下搜索效率低、实时性差的问题[6,7]，但并未考虑行车的安全问题，且生成的路径折角较多，并不符合机器人的实际运动需求。因此，在BIT算法的基础上增加障碍物膨胀与曲线优化，进而提升机器人移动的安全性和稳定性。

1 BIT算法原理

1.1 BIT算法基本原理

与传统的基于图搜索的A星算法与基于随机采样的RRT算法均不同，BIT算法结合两者优势，其首先对自由空间进行随机采样，利用采样点、起点与终点构建起隐式随机几何图（Random Geometric Graph，RGG），随后通过启发式搜索扩展搜索树，在成功找到路径后，缩小采样范围。与RRT相比，其构造树的过程不直接对边进行碰撞检测，而是只有当边线为队列最佳边时，才对其进行碰撞检测，由此减少非必要的运算[8]，同时在每次批量采样前，对搜索树进行修剪，删去无助于提高路径成本的节点与边线，进而极大提升算法的运算速度和收敛速度。其主体的伪代码见表1，其主要包括批量采样、扩展及修剪树模块等，详细步骤可见参考文献[5]。

1.2 数学约定

为便于算法讲解，对Alg1中的相关参数进行数学约定。

Alg1.Line1:SettingUpPlanning()为初始化函数，该函数所涉及的数学约定，QE为有序连线集合，其序列第一个元素表示代价值最小的边及其代价值。QV为有序节点集合，其序列第一个元素表示代价值最小的节点及其代价值。E为树模型中的连线集合，E集合中的每个元素用(v,w)表示，且v,w∈V。V为树模型中的顶点集合。φ为空集；xstart表示起点坐标；xgoal表示终点坐标；Xsamples为采样点集合；r为隐式RGG算子。

Alg1.Line4:gT(xgoal)为根据随机树搜索路径到达目标点所需的代价。

Alg1.Line5:m为每次采样点的个数，表示集合的并操作。

Alg1.Line6:Vold为旧顶点集合。

Alg1.Line7:Vnum表示V集合元素的个数，Xsamplesnum表示Xsamples集合元素的个数。

Alg1.Line10:vm、xm表示边队列中代价值最小边对应的两个顶点。

Alg1.Line13-22:g'(v)为v点与起始点的欧拉距离；c'(v,x)为v点与x点之间的欧拉距离；h'(x)为x点与终点的欧拉距离；c(vm,xm)为vm点与xm点之间的实际距离（包含碰撞检测）。

1.3 BIT算法程序实现

BIT算法伪代码见表1。

表1 BIT算法伪代码Table 1 BIT Algorithm pseudo code

首先对算法进行初始化操作，将QE、QV、E置空，起始点xstart插入V，目标点xgoal加入采样点集合Xsamples，并设置r=∞（Alg.1,Line1）。

随后进入循环，若QV和QE为空，则进入修剪树(Alg.1，Line4)和批量采样(Alg.1，Line5)步骤。

修剪与批量采样完成后，将当前顶点集合加入Vold中进行记录，并将顶点集V加入QV顶点队列进行排序，队列最前端元素为代价值最小的顶点及其代价(Alg1.Line6)。

之后，计算r算子(Alg1.Line7)，其可通过式（1）计算获得：

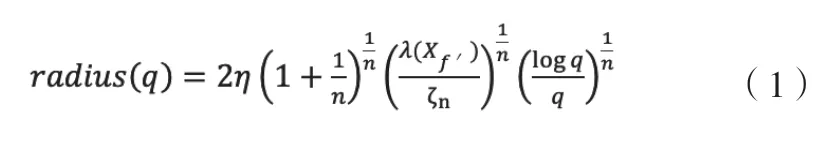
式（1）中：λ()——一个集合的勒贝格测度。

Xf '——{x∈X│f '(x)≤cbest}。

n——求解空间的维度。

ζn——n维单位球的勒贝格测度。

q——Vnum+Xsamplesnum。

Vnum——V集合元素的个数。

Xsamplesnum——Xsamples集合元素的个数。

η——自适应调整参数，η≥1。

bestVertexValue与bestEdgeValue分 别 返 回QE、QV队列中的最小代价值及其对应的顶点和边，只要满足循环条件，则持续对顶点队列中代价值最小的点进行扩展，随后提取边队列中的最优边(vm,xm)，将其从QE队列中删除(Alg1.Line8-11)。

CheckValues(vm,xm)用于检验获得的(vm,xm)边是否满足gT(vm)+c'(vm,xm)+h'(xm)＜gT(xgoal)、g'(vm)+c(vm,xm)+h'(xm)＜gT(xgoal)、gT(vm)+c(vm,xm)＜gT(xgoal)3个扩展条件，若均满足则检查点xm是否已在树中，若树中已存在点xm，则将E中所有与xm相连的边(v,xm)去除(Alg1. Line14)；若xm不在树中，则从采样点集合Xsamples中删除点xm，并将点xm加入V、QV中(Alg1.Line16-Line17)。随后将边(vm,xm)加入集合E，遍历QE中以xm为终点的边，若满足gT(v)+c'(v,xm)≥gT(xm)，则将(v,xm)从QE中删除(Alg1.Line18-19)。

若不满足Alg1.Line12，则表示所有的采样点都不可能对当前解进行优化，则将QE、QV置空，随后进入Alg1.Line2重新采样计算(Alg1.21)。

在满足结束要求后，返回求解出的搜索树T(V,E)（Alg1.Line22-23）。

1.4 修剪树

修剪树模块的函数为Prune(gT(xgoal))。gT(xgoal)为根据搜索树路径到达目标点的实际代价。该步骤旨在去除搜索树中对优化解无用的点和边，以提升搜索效率，减少搜索的盲目性，其主要为剔除采样点集合、树顶点集合和树连线顶点集合中从起点经过该点到达目标点所需预估代价大于当前最优路径代价的点。

1.5 扩展

扩展模块的函数为expandVertex(v)，表示对v顶点进行扩展操作。其首先将bestInVertexValue()函数所获得的最小代价值点v从队列QV中取出，后计算采样点中与点v的欧拉距离小于r的临近点集合。遍历临近点集合，若此临近点x与点v的连线能够满足g'(v)+c'(v,x)+h'(x)＜gT(xgoal)，则将两点连线所形成的边插入队列QE。

1.6 批量采样

Sample(m,gT(xgoal))为批量采样功能函数，其在未找到可行路径状态下在全地图自由空间进行批量采样，在通过搜索树成功寻找到路径后，则缩小采样范围，转变为在椭圆区域的自由空间内进行采样。其椭圆采样空间的计算方法如图1。

图1 椭圆采样空间Fig.1 Elliptical sampling space

长轴为cbest,为当前到达目标点的最优路径长度，短轴的计算方法为，cmin为起始点与目标点间的欧拉距离，在实际运算中，可先在标准圆中进行采样，并对采样点进行矩阵运算，使其平移旋转至椭圆区域。

此方法能够在寻找到初始解后有效地提升算法收敛速度。

2 Bezier曲线优化

在路径规划过程中，通常会产生一条具有多个锐角或拐角的路线，这种路径不适合实际作业中携带大量物品的移动机器人[9]。因此，为了使搬运机器人能够更加稳定地完成其任务，需要对生成的路径进行平滑处理。

Bezier曲线是一种通过较少控制点便能生成复杂平滑路径的方法，目前被广泛应用于汽车车体工业设计、计算机辅助设计、路径规划等领域。以二阶贝塞尔曲线为例，其生成过程如图2。

为便于理解，图2选取5个特殊比例来求解其对应的贝塞尔曲线点，在实际运算中，其选取线段长度与对应边长度的比例为t(t∈[0,1])，可以取无穷多个，从而形成整条贝塞尔曲线。

图2 二阶贝塞尔曲线生成过程Fig.2 Generation process of third-order Bessel curve

如图2所示，Pi(i=0,1,2)为形成贝塞尔曲线所需要的控制点，Li(i=0,1,…,3)为线段P0P1上的点，Ki(i=0,1,…,3)为线段P1P2上的点，Ti(i=0,1,…,3)为贝塞尔曲线上的点，其几何关系满足：

扩展到一般情况，其数学表达式如式（2）、式（3）表示：

式中：n——拟合点个数。

t——线性插值比例，t∈[0,1]。

i——i∈{0,1,…,n}。

由式（2）、式（3）可得，一阶Bezier曲线的表达式为：

二阶Bezier曲线为：

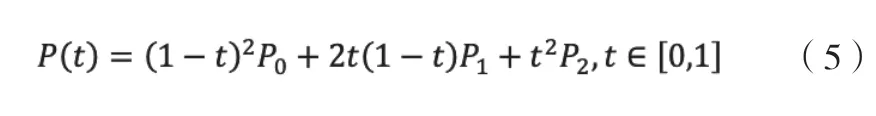
三阶Bezier曲线为：

式中：Pi——第i个点。

k阶Bezier曲线需要k+1个点进行求解。在实际运用中，随着Bezier曲线阶数的增加，其运算复杂度呈几何倍增长，而三阶Bezier曲线能够保证机器人运行时其速度、加速度均为连续的同时，又不会严重影响运算速度，符合机器人的运动控制要求，因此采用三阶Bezier曲线对点进行拟合。

将三阶Bezier曲线进行拟合优化,则优化后的曲线点为：

式（7）中：xi——第i点的x坐标。

yi——第i点的y坐标。

x、y表示Bezier曲线的拟合点坐标。

三阶贝塞尔曲线优化与BIT结合的具体算法步骤见表2。

表2 Bezier曲线优化伪代码Table 2 Bezier curve optimization pseudo code

3 仿真实验与结论

在Intel i7-6700HQ笔记本电脑上使用Python 3.9，并在Anaconda3环境下对原始BIT算法、障碍物膨胀及其Bezier曲线优化后的算法进行仿真实验。

本文路径规划的障碍物仿真环境如图3，其为几何地图，总尺寸为240m×240m，地图中心为原点坐标(0,0)，xstart=(-95,-95)，xgoal=(60,85)，每批次采样点个数200个，r算子η系数为1.1，障碍物膨胀度为5m。本文以圆形机器人为仿真模型，其半径为R，使机器人以1m/s的速度严格沿生成路径行驶。通常情况下，障碍物的膨胀度应略大于机器人的半径R，以此保证机器人在沿路径行驶的过程中不会发生碰撞。

其中，图3左下方为起点xstart,右上方为目标点xgoal，地图中的圆形障碍物以(x,y,r)形式进行表示。其中，x、y为圆心坐标，r为半径。

图3 障碍物分布Fig.3 Obstacle distribution

图4为BIT未经过障碍物膨胀和曲线优化，运行迭代10000次后生成的路径，其生成路径与障碍物距离过近，多个障碍物与路径相切，因此在实际环境中无法满足机器人安全行驶的需求。

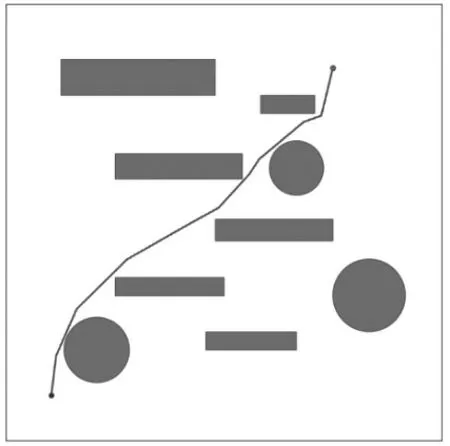
图4 原算法路径图Fig.4 Original algorithm path diagram

因此，对障碍物进行膨胀操作，膨胀后的障碍物地图如图5。

图5 膨胀地图Fig.5 Expansion map

图6为对地图障碍物向外膨胀5m后，算法运行迭代10000次后生成的路径。由图6可知，其求解出的路径距离障碍物均大于5m，虽然能够满足机器人运行的安全性，但仍存在一定折角。

图6中的路径坐标见表3。

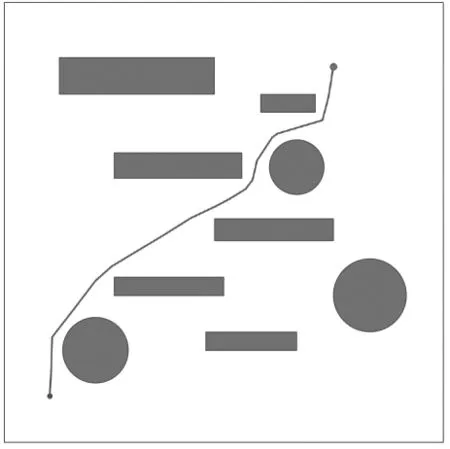
图6 膨胀操作后的路径图Fig.6 Path map after expansion operation

取表3中每行两点坐标形成连线，不考虑点(60.00，85.00)，计算两点连线的斜率，并绘制成折线图如图7。

表3 路径点坐标Table 3 Path point coordinates

由图7可知，其波动较大，在机器人实际运行过程中，会表现为运行至折角处速度发生突变并快速转向，不利于机器人在真实搬运环境下的平稳运行。

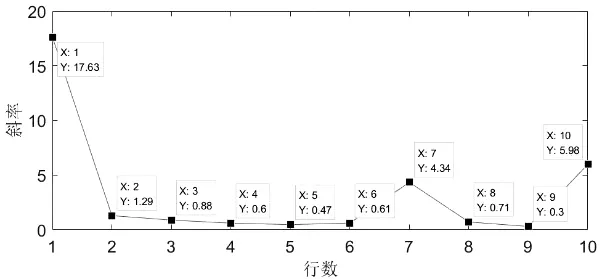
图7 斜率变化折线图Fig.7 Line chart of slope change

增加障碍物膨胀后的算法迭代过程如图8，其横坐标为时间，单位：秒（s），纵坐标为路径代价。算法在0.09678s后成功寻找到最初路径，并快速收敛，在2.037s后寻找到次优路径，与最优路径259.1的代价值相差仅为4，并最终在9.57s时收敛至最优。

图8 增加障碍物膨胀后的迭代过程Fig.8 Iteration process after adding obstacle expansion

图9为本文在图6基础上加入Bezier曲线优化后得到的路径，其路径代价值为258.88，与原先最优路径相比，其代价值减少了0.22，路径更加平滑，更适合机器人的平稳运行。

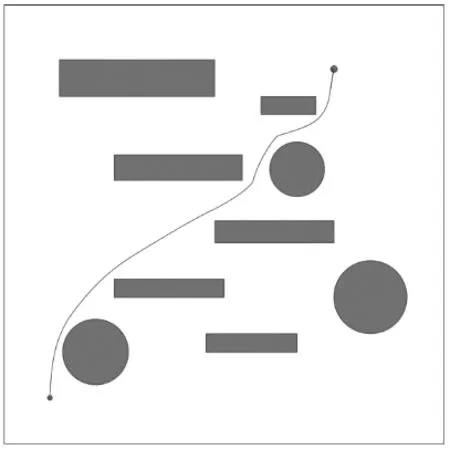
图9 Bezier曲线优化后的路径Fig.9 Optimized path of Bezier curve

仿真实验结果表明，经过障碍物膨胀和曲线优化后的BIT算法在复杂环境和大场景范围下仍能够快速求解出路径并迅速收敛，并能在减小路径的代价值的同时使得机器人的运行更加平稳，能够满足农业大场景下的路径规划要求。