瑞利面波椭圆极化在盾构隧道地层扰动探测中的应用

王 天 ，张 立 ，陈雨翔 ，孙 康 ，刘争平 ，冯 栋 ，陈善林

（1. 西南交通大学地球科学与环境工程学院，四川 成都 610031；2. 湖南省交通规划勘察设计院有限公司，湖南 长沙 410200）

随着国内城市盾构隧道的发展，盾构施工引发的地面塌陷事故对人民生命财产安全造成严重威胁[1-2]. 为避免此类事故的发生，在盾构施工过程中对其产生的变形或沉降[3]等进行了监控测量[4]，但这些测量都是在沉降或变形等发生后才能进行的，因此很难实现提前预警. 近年来，人们开始采用物探方法，通过对介质物性参数变化的观测，实现对介质变形、沉降以及可能形成的空洞和塌陷等的探测和监测，如探地雷达、瑞利面波法等[5-9]. 但探地雷达精度虽高，勘探深度却有限，传统瑞利面波速度频散方法由于需要长大检波器排列，因此在数据采集上易受场地限制，尤其是人口密集、交通繁忙的城市等地.为解决传统速度频散瑞利面波法在应用中存在的问题，研究者们开始关注瑞利面波另一重要特征，即椭圆极化特征，该方法可通过单个三分量检波器采集信息[10]，不易受场地限制，能更好适应城市背景下的检测或勘探任务.

早在1969 年，Boore 等[11]首先提出利用瑞利面波椭圆极化率来研究地壳结构的可行性；Taner 等[12]计算了单个三分量检波器采集的地脉动信号水平与垂直分量的傅里叶变换频谱比，并提出了单点H/V谱比法（H、V分别为地震记录面波时间域信号水平分量、垂直分量）；Tokimatsu 和Miyadera[13]发现，地脉动H/V谱比对场地横波速度Vs变化的响应特征与基阶瑞利面波椭圆极化率对Vs的响应特征是一致的；蒋通等[14]讨论了地脉动实测H/V计算方法的可靠性，并据此评价场地的卓越周期；Arai 等[15]指出地脉动H/V谱比主要反映的是瑞利面波或勒夫波的椭圆极化率，其对地层速度变化的灵敏度比速度频散高；张立[16]推导了水平层状介质中瑞利面波质点位移解析解，结合地脉动单点谱比法通过数值模拟得到层状介质中主动源瑞利面波的椭圆极化频散，展示了利用单点瑞利面波的多分量评价地层泊松比结构的可行性；于文福[17]利用有限元方法开展了横向非均匀介质中瑞利面波椭圆极化率频散数值模拟研究，验证了瑞利面波椭圆极化率与介质泊松比之间的线性反比关系.

目前对瑞利面波椭圆极化的相关研究和应用尚处于探索阶段，在此前提下，依据城市盾构隧道工程实例，通过结合传统瑞利面波速度频散方法与主动源椭圆极化频散方法对其进行数值模拟研究和实际案例应用对比，探讨主动源瑞利面波椭圆极化频散方法在城市盾构隧道上覆地层扰动探测和地面塌陷监测中应用的可行性，为今后类似探测和监测工作提供参考.

1 基本原理

1.1 有限元数值模拟原理

基于地震波原理，应用有限元数值模拟软件，对城市地下盾构隧道开挖引起地层扰动的地震全波场特征进行数值模拟研究[18-19].

本文研究采用的是零相位、主频24 Hz 的宽带雷克子波作为震源函数，如式（1）.

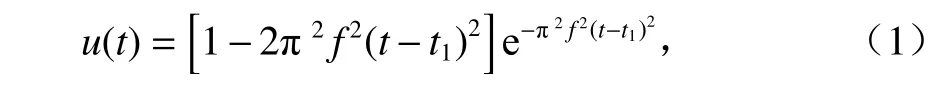
式中：u(t)为载荷大小，t为时间；t1为雷克子波主峰时间；f为雷克子波主频.

1.2 瑞利面波频散曲线提取方法

通常情况下地震波并非单一频率的简谐波，而是由多个不同频率的波叠加而成，此频散现象存在于非均匀介质中[20-21]. 由于瑞利面波产生在自由表面附近，其振幅随深度衰减，穿透深度约为一个波长，因此不同频率穿透深度不同. 高频即较短波长的波采样浅层，相反，低频即较长波长的波采样深层. 因此，不同频率波的传播速度各异，地层速度也随深度变化，这种传播速度随频率变化的现象，即为速度频散Vr(f).

频率-波数（f-k）变换是目前提取面波频散曲线应用较为广泛的方法之一. 通过对原始x-t域地震记录作二维傅里叶正变换使其变换到f-k域，其中二维傅里叶正变换式为

式中：ω为圆频率；u(x，t)为原始地震记录，G(ω，k)为经过二维傅里叶变换后得到的地震数据.

f-v（频率-速度）变换则是在f-k变换基础上，利用波数和速度、频率之间的关系变换到f-v域再进行频散曲线提取，其关系式为

1.3 瑞利面波椭圆极化提取方法

根据前期研究成果，与速度频散特性相似，在非均匀介质中瑞利面波椭圆极化率Er也会随着频率f的变化而变化[22]，即为椭圆极化频散Er（f），然而对于均匀介质，椭圆极化率是一个固定常数. 目前计算瑞利面波椭圆极化频散的方法主要是H/V谱比法[23-24]，其计算式为

式中：H(f)为水平位移频谱；V(f)为垂直位移频谱.

对于瑞利面波在自由表面传播，其椭圆极化率E0的计算式为

2 有限元数值模拟

2.1 数值模拟模型

盾构隧道施工时开挖面支护压力较小，掘进后容易在盾构上方形成空洞，随着土拱作用，空洞顶部土体逐渐向下脱落，空洞逐渐向上方地表发展，最后导致地表塌陷[25-26]. 本文根据上述盾构隧道施工引发的滞后地面塌陷机理，结合长沙万家丽路220 V 电力隧道里程300—370 段实例施工方案及实际地质等情况，首先从均匀模型（图1（a））瑞利面波数值模拟研究出发，并根据实际上覆地层埋深8～15 m 和盾构隧道外径4.1 m 情况，建立盾构隧道模型（图1（b）和图1（c））、盾构开挖后形成的空洞初期模型（图1（d））以及空洞向地表发展模型（图1（e））.

本文数值模拟研究采用的是多道瞬态瑞利面波观测排列[27]，最小偏移距为40 m，共51 个检波器沿测线依次排列，道间距为1 m. 采样时间1.024 s，时间步长为0.000 5 s. 模型中原状粉质黏土和疏松状粉质黏土分别用编号1、2 代表，介质参数的取值以实际地质情况为参考，因无特殊岩性与地质构造，故采用一般均质岩土弹性参数，其模型主要参数如表1.

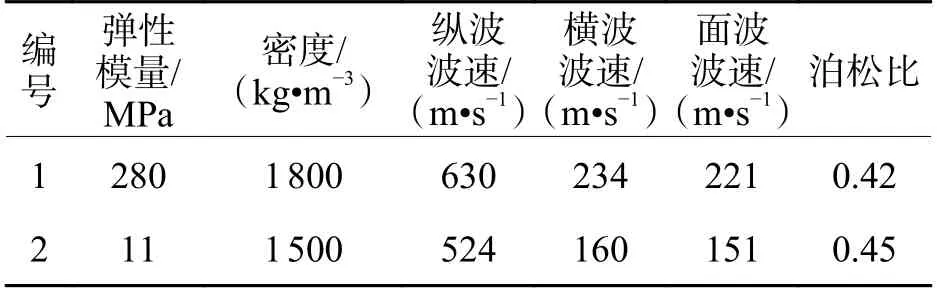
表1 数值模型介质参数Tab. 1 Medium parameters of numerical model

2.2 结果与分析

基于有限元软件对图1 中各模型进行二维模拟仿真，并对模拟结果进行波场传播、速度频散以及椭圆极化频散等特征的相关研究，特征分析如表2所示.

表2 数值模拟结果特征分析Tab. 2 Characteristic analysis of numerical simulation results

图1 盾构隧道数值模型观测排列示意Fig. 1 Observation arrangement for numerical model of shield tunnel

2.2.1 均匀介质模型

均质模型（图1（a））数值模拟结果如图2 所示.

在图2（a）中：通过偏移距与时间的关系可以算出波速，与模型设定（表1）的理论速度630 m/s （Vp）和221 m/s （Vr）基本吻合；根据研究发现，对于瑞利面波无论选用水平分量还是垂直分量，提取的频散曲线基本是一致的[28]. 图2（b）中：由于体波等干扰，图中近源场区可看到面波速度有一定的低速区，而在偏移距较大、面波能量占优的远场区，速度频散剖面显示则较为均匀，即没有频散现象；由已有研究[17]可知，均匀介质中震源近场区由于体波等干扰，椭圆极化率值Er会呈现放射状高低值交替现象，随着偏移距增大，即在远场区，这种现象逐渐减弱. 从图2（c）中可看出：随着偏移距的增大，Er整体趋于均一，说明在均匀介质震源远场区，Er与速度频散特征类似，也是一个常数，即没有频散现象.

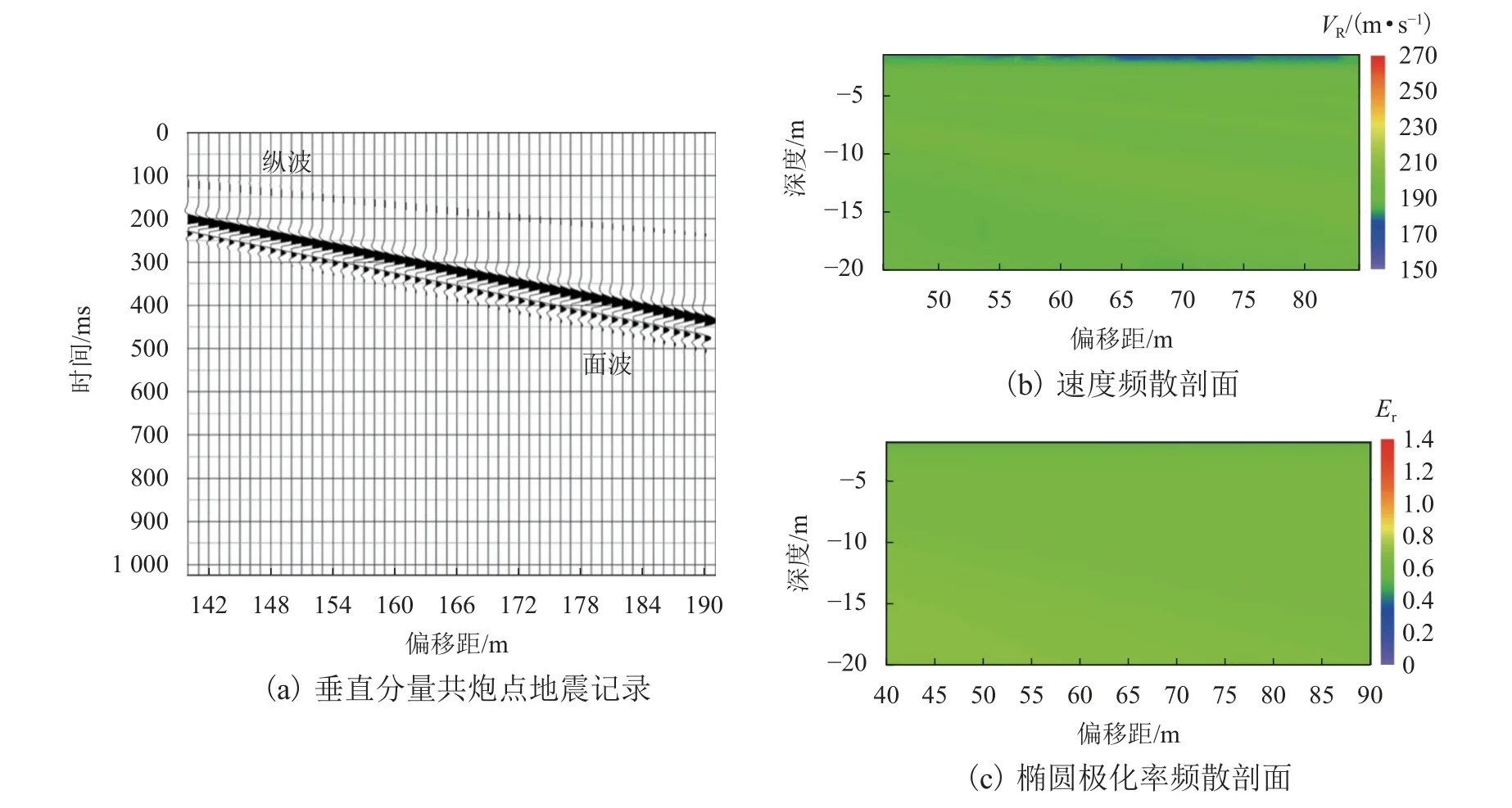
图2 均匀模型数值模拟成果Fig. 2 Numerical simulation results of homogeneous medium model

2.2.2 盾构隧道横剖面模型

盾构隧道横剖面模型（图1（b））数值模拟结果如图3 所示.

由图3 可知：通过能量大小关系可以清楚辨别出最上方直线同相轴为直达纵波DP，其下方能量最强的直线同相轴是面波R，其弧形同相轴顶点位于第25 个接收点附近，即对应偏移距65 m 处、隧道横剖面位置（虚线处），则可知弧形曲线是直达波和面波在遇到隧道横断面时发生的反射波或转换波等；速度频散分析能够较准确地反映出隧道横剖面及周围介质的相对位置；此模型模拟结果（图3（c））与邓瑞[29]研究中所述均匀介质中局部空洞模型的Er异常呈“左高右低”现象[29]相一致. 因此，由数值模拟结果可知，盾构隧道横剖面上Er具有特定异常分布现象，且Er与介质泊松比之间存在一定对应关系[17,22]，即椭圆极化频散方法能够有效识别隧道在横剖面上的分布结构.

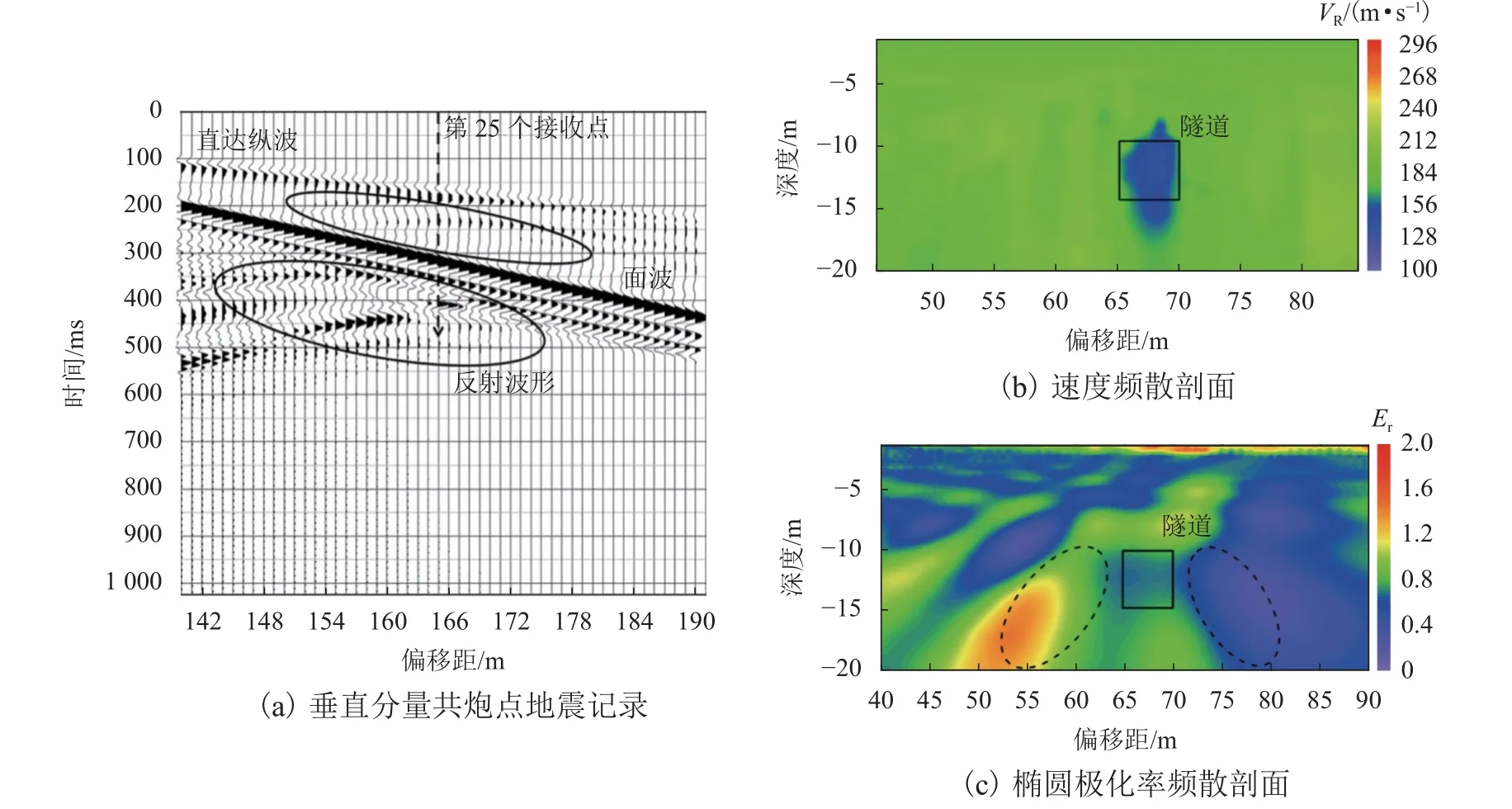
图3 盾构隧道横剖面模型数值模拟成果Fig. 3 Numerical simulation results of transverse section model of shield tunnel

2.2.3 盾构隧道纵剖面模型

盾构隧道纵剖面模型（图1（c））数值模拟结果如图4 所示.

图4（a）中：由于沿隧道纵剖面方向，震源激发产生的地震波主要在上层区域内即隧道上壁界面和地表之间来回反射叠加，并在界面和地表处发生波型转换和生成新的面波，从而上层区域内各种波的叠加使得局部范围内波振幅增大或减小，因此在地震记录图上呈现为隔一定时间和距离即x-t间隔出现一组同相轴的波形[30]. 图4（b）中：由于隧道挖空，沿隧道纵剖面方向地震波能量难以穿透空气向下传播，可看出隧道及以下区域都呈明显低速特征；可发现传统速度频散方法能够较好地反映出隧道所处位置及介质分层情况. 图4（c）中：椭圆极化值Er呈区块状不均匀分布，与上述地震记录中出现的时强时弱的同相轴地震波密切相关，均为地震波在上层区域内来回反射叠加使局部范围内波振幅增大或减小，从而造成局部区域内按H/V谱比方法计算所得的Er值偏大或偏小的区块现象；隧道上方介质Er虽呈较不均匀的区块分布，但整体明显比下方介质高. 因此，Er在隧道纵剖面结构分布上具有明显差异特征，能够对隧道纵剖面分层情况进行有效识别.

2.2.4 盾构隧道上方空洞初期模型

对空洞形成初期模型（图1（d））进行数值模拟，结果如图5 所示.

由图5 可知：图5（a）中地弧形曲线是地震波遇到隧道上方空洞时发生的反射波所形成；速度频散方法对隧道纵剖面分层及开挖形成的初期空洞都能有效识别；与图3（c）和图4（c）对比可发现，图5（c）上新形成的空洞位置附近出现了明显类似图3（c）的椭圆极化率异常现象，且隧道上层介质中其他高Er值区块的形成与图4（c）类似，是地震波在地表和隧道壁之间相互反射叠加的结果. 因此，椭圆极化频散方法能够较好地分辨出盾构隧道在纵剖面上的结构情况，并且能有效识别出隧道上方形成的局部空洞异常.

图4 盾构隧道（纵剖面）模型数值模拟成果Fig. 4 Numerical simulation results of longitudinal section model of shield tunnel

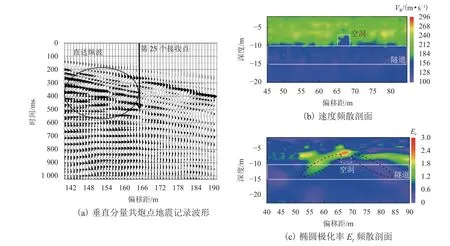
图5 盾构隧道上方空洞初期模型数值模拟成果Fig. 5 Numerical simulation results of initial cavity model above shield tunnel

2.2.5 盾构隧道上方空洞向地表发展模型

盾构隧道开挖引起的上方空洞随着时间推移逐渐向地表发展，对此时空洞发展模型（图1（e））的数值模拟结果如图6 所示.

图6 盾构隧道上方空洞向地表发展模型数值模拟成果Fig. 6 Numerical simulation results of development model of shield tunnel cavity to ground surface

图6（a）通过与图5（a）的对比可发现：如表2 模型e 所述的弧形同相轴特征出现的时间更早，弧形特征更为明显. 造成该现象的原因一方面是因为空洞上移后埋深变浅，另一方面是因为空洞发展过程中掉落的土体相对周围介质较为疏松，从而使空洞发展轨迹范围内都属于低速区域，因此随着低速区域范围的变浅和增大，弧形反射波特征出现的时间也更早、更明显. 通过对比图5（b）可见：图6（b）的速度频散方法对隧道纵剖面结构分层及隧道上方局部空洞和空洞发展状态均有非常好的识别效果. 如图6（c）所显示，通过与图4（c）及图5（c）对比可看到：随着空洞位置上移，空洞和低速异常区域范围扩大，空洞下方Er值分别向两侧斜下方呈高低相间放射状排列的现象出现的时间更早、特征更加明显. 通过Er分布规律能够较好分辨盾构隧道纵剖面结构的基础上，能够进一步有效识别出隧道上方局部空洞分布及规模，即该方法能够对介质中空洞的发展状态进行有效监测.

通过研究发现：Er频散和FV方法都能够对隧道开挖引起的上方空洞及空洞发展引起的地表塌陷进行有效探测和监测，且Er频散方法具有不需要长大的检波器排列的优点，因此更适合城市等场地受限的情况. 对图1（a）、（b）、（c）模型的数值模拟正是参照本文实际工程案例的施工方案和地质情况，分别对盾构隧道开挖前和开挖后纵剖面与横剖面实际情况进行仿真研究，而下文则是对实际案例采集数据的相同处理分析.

3 应用实例

3.1 工程概况

以长沙万家丽路220V 电力隧道里程300—370 段为例. 本工程北起国防科技大学三号院北侧马栏山变电站，向东铺设至万家丽路、特立路交叉路口，本段地貌单元属于丘陵地貌，在特立路口向南拐弯至开福区福元路，沿既有万家丽路向南，纵贯开福区、止于芙蓉区之火炬路，主要为浏阳河冲积阶地，地貌单元为典型河流侵蚀堆积地貌. 该段采用盾构法施工，隧道内径3.6 m，外径4.1 m，电力隧道顶面覆土厚度为8～15 m.

3.2 采集参数

由于现场公路交通繁忙，测线布置在隧道顶部地表沿轴线走向. 采用DAQlink-Ⅲ分布式地震仪，主频4 Hz 的三分量检波器，选定主动源方式采集数据，采样时间0.512 s，采样率0.062 5 ms，测量时间分别在开挖前原状态时和开挖7 d 后地表相对位移沉降稳定时进行，具体测线布置如图7 所示.

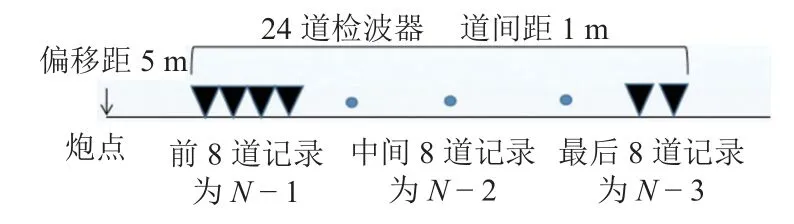
图7 现场数据采集布置示意Fig. 7 Layout of field data acquisition

3.3 数据处理及解释

首先对开挖前和开挖后第7 d 两次采集的数据进行前期编辑和预处理后：对垂直分量数据经过FK滤波（率波数域滤波）等处理后提取速度频散曲线，绘制速度频散剖面图；对水平分量和垂直分量经过频谱计算等处理后，对其进行频谱比即Er计算，并绘制Er频散剖面图，最后结合地质资料等对隧道开挖前后速度频散和Er频散成果图进行分析和解释.

3.3.1 盾构隧道开挖前

隧道开挖前垂直分量速度频散剖面及HV分量椭圆极化Er频散剖面分别如图8（a）、（b）所示，从图8 可知：在隧道深度范围以内，整个测区在隧道开挖前速度和Er值分别为190～250 m/s 和4.4～5.0，面波速度Vr和Er整体分布都较为均匀，没有明显大范围的空洞等低速或低泊松比的异常现象，该现象与前期勘察地质资料结果相符.

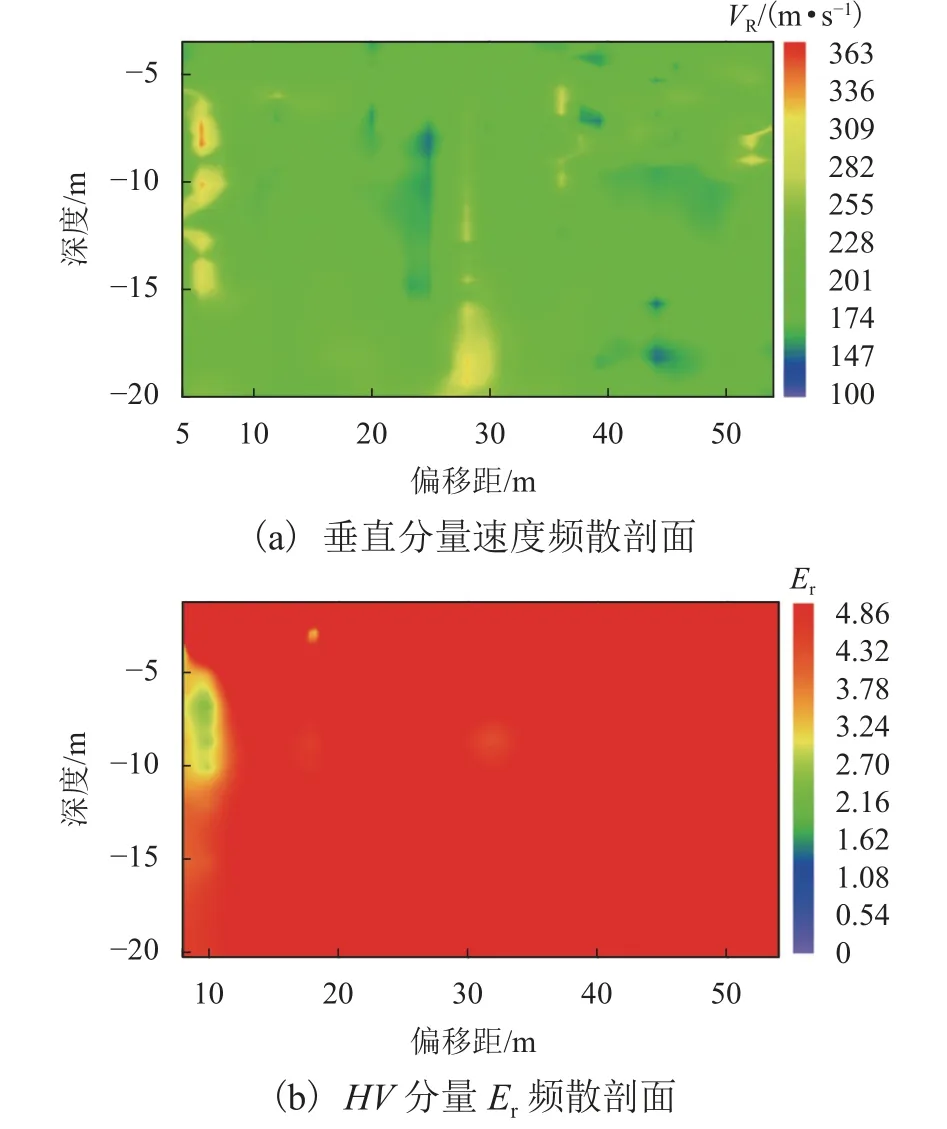
图8 实例（盾构隧道开挖前）解译Fig. 8 Projecte interpretation diagram （before shield tunnel excavation）

3.3.2 盾构隧道开挖后

盾构隧道开挖后垂直分量速度频散剖面和HV分量Er频散剖面如图9 所示，其中白色水平线之间为隧道位置. 由图9 可知：在隧道上壁界面附近出现V和Er分界面，其中速度频散剖面中隧道下层介质呈明显低速特征，Er则为低泊松比特征.

由两种方法对比可看到，瑞利面波椭圆极化频散方法同样可以达到速度频散方法对地下岩土介质结构有效判识的效果. 此外，根据前面对隧道开挖形成的空洞初期及发展中状态的数值模拟特征分析，此次工程实例中未见有明显类似空洞的特征出现，结合现场地质勘察等资料证实确实没有空洞存在.图9（a）中低速区块可能是因为在交通繁忙的公路边，现场采集数据质量较差所造成的速度频散曲线拾取产生偏差，相对而言，通过对HV分量频谱比计算所得的Er频散方法对此类干扰具有较强的抵抗性，因此在对应的Er频散图上没有明显的空洞Er放射状现象.

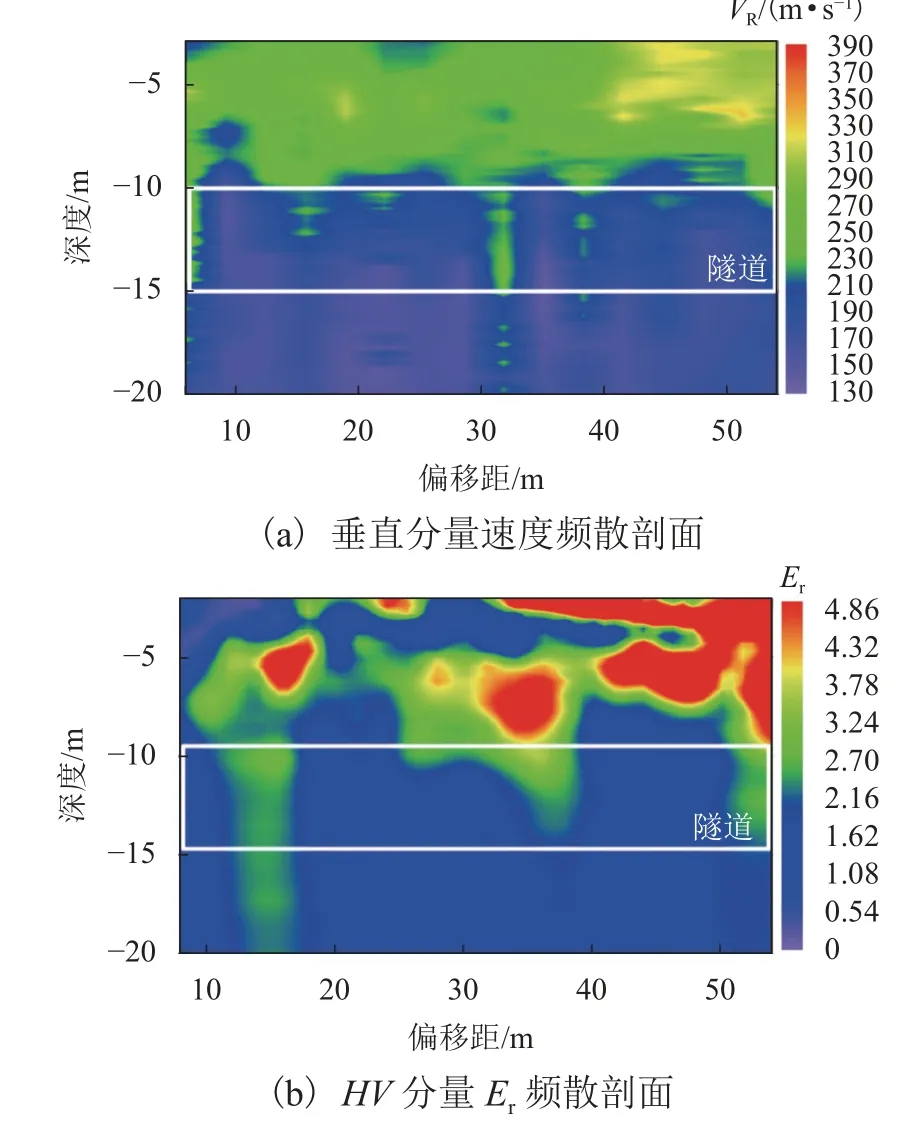
图9 实例解译（盾构隧道开挖后）Fig. 9 Projecte interpretation diagram （after shield tunnel excavation）

根据以上工程实例研究发现：椭圆极化频散方法不仅具有传统速度频散方法类似的探测效果，能够探测和监测地下介质的结构分布及比变化状态，并且不需要长大检波器排列，对现场震动噪声也具有较强的抗干扰性，由此可见，椭圆极化频散方法具有更广的应用范围和应用前景.

4 结 论

本文在以城市盾构隧道上覆地层扰动探测和地面塌陷监测为例，对其进行了正演数值模拟研究，并结合工程实例进行了应用研究,对比分析得到以下结论：

1） 数值模拟结果中，对于地下介质的结构分布以及横向非均匀体如空洞等异常体的探测，相比传统成熟的速度频散方法，主动源利面波椭圆极化方法，具有类似的探测效果，且该方法可实现单点采集，不受场地限制，并且处理步骤更为快捷，受周围噪声干扰影响相对较小，因此在采集和处理上具有更高的效率.

2） 相比传统方法不能对城市盾构隧道施工中出现的地面塌陷等情况进行及时预警的问题，瑞利面波椭圆极化方法可以在不受场地限制的情况下，对上覆地层受到扰动后结构发生变化的情况进行无损探测和监测，因此可以对可能发生的塌陷等灾害进行及时预警，从而可以避免重大的人民生命财产损失.